Яндекс.Блиц. Почему и какие алгоритмические задачи нужно уметь решать, работая в поиске

в 7:30, , рубрики: C#, c++, java, python, Алгоритмы, Блог компании Яндекс, задачи для программистов, задачи для собеседований, занимательные задачи, математика, собеседование

Редко когда кандидат проходит только одно техническое собеседование — обычно их несколько. Среди причин, почему человеку они могут даваться непросто, можно назвать и ту, что каждый раз приходится общаться с новыми людьми, думать о том, как они восприняли твой ответ, пытаться интерпретировать их реакцию. Мы решили попробовать использовать формат контеста, чтобы сократить количество итераций для всех участников процесса.

Яндекс.Блиц. Почему и какие алгоритмические задачи нужно уметь решать, работая в поиске - 1

Для Блица мы выбрали исключительно алгоритмические задачи. Хотя для оценки раундов и применяется система ACM, в отличие от спортивного программирования все задания максимально приближены к тем, которые постоянно решают в продакшене Поиска. Те, кто решит успешно хотя бы четыре задачи из шести, могут считать, что прошли первый этап отбора в Яндекс. Почему алгоритмы? В процессе работы часто меняются задачи, проекты, языки программирования, платформы — те, кто владеет алгоритмами, всегда смогут перестроиться и быстро научиться новому. Типичная задача на собеседовании — составить алгоритм, доказать его корректность, предложить пути оптимизации.

Квалификацию можно пройти с 18 по 24 сентября включительно. В этом раунде вам нужно будет написать программы для решения шести задач. Можете использовать Java, C++, C# или Python. На всё про всё у вас будет четыре часа. В решающем раунде будут соревноваться те, кто справится как минимум с четырьмя квалификационными задачами. Финал пройдёт одновременно для всех участников — 30 сентября, с 12:00 до 16:00 по московскому времени. Итоги будут подведены 4 октября. Чтобы всем желающим было понятно, с чем они столкнутся на Блице, мы решили разобрать пару похожих задач на Хабре.

1. Robust Execution Manager

Первая задача связана с одной из систем обработки данных, разработанной в Яндексе, — Robust Execution Manager, REM. Он позволяет строить сложные процессы, включающие множество разных операций, и устанавливать зависимости между ними. Так, решение многих задач связано с обработкой пользовательских логов, содержащих информацию о заданных запросах, показанных документах, совершённых кликах и так далее. Поэтому вычисление поискового фактора CTR (click through rate, отношение числа кликов по документу к количеству его показов) зависит от задач обработки пользовательских логов, а от решения задачи вычисления CTR зависит задача доставки значений этого фактора в поисковый runtime. Таким образом, REM позволяет выстраивать цепочки обработки данных, в которых поставщик данных не обязан знать о том, кто эти данные в дальнейшем будет использовать.

В процесс исполнения цепочек обработки могут быть внесены коррективы. Например, уже после построения поисковых логов может выясниться, что значительный объем данных был доставлен с существенной задержкой, и поисковые логи необходимо перестроить. Естественно, после перестроения логов необходимо также перезапустить все процессы, которые от них зависели. Другой пример того же рода — попадание в пользовательские логи запросов, выполненных нашим поисковым роботом. Эти запросы не являются запросами пользователей, а поэтому вносят шум в вычисление поисковых факторов, расчёты экспериментов и так далее. Поэтому в этом случае логи также нужно обновить, после чего перезапустить все процессы их обработки. Поэтому REM поддерживает операцию обновления данных с последующим перезапуском всех задач, зависящих от этих данных.

1.1. Постановка задачи

Задача заключается в реализации именно этой операции. Входными данными будет ациклический ориентированный граф с выделенной вершиной. Граф описывает некоторый процесс обработки данных, при этом вершины представляют этапы этого процесса, а рёбра — зависимости между ними. Выделенная вершина соответствует одной из подзадач, которую необходимо перезапустить из-за изменений в данных. После перезапуска необходимо будет также перезапустить и все подзадачи, зависящие от неё по данным. Необходимо написать программу, которая выводит список этих подзадач, причём в порядке, в котором их необходимо будет перезапустить.

1.2. Решение

Рассмотрим для начала решение задачи в случае, когда вершины из ответа не нужно упорядочивать. Тогда задача решается достаточно просто: запустим из выделенной вершины любой алгоритм обхода графа (например, обход в глубину), и запишем в ответ все посещённые вершины. Действительно, если задачи с номерами $j_1$, $j_2$, ..., $j_k$ зависят по данным от задачи $i$, то после перезапуска задачи $i$ необходимо перезапустить все эти задачи, а также те задачи, что зависят уже от них. Кроме того, каждую вершину нужно вывести ровно один раз. Оба этих условия обеспечиваются стандартными методами обхода графов.

Так может выглядеть решение для данной задачи

#include <iostream>
#include <vector>

using Graph = std::vector<std::vector<int>>;

void DFS(const Graph& graph,
         const int vertice,
         std::vector<bool>& used,
         std::vector<int>& result)
{
    used[vertice] = true;
    result.push_back(vertice);

    for (size_t idx = 0; idx < graph[vertice].size(); ++idx) {
        const int adjacent_vertice = graph[vertice][idx];
        if (!used[adjacent_vertice]) {
            DFS(graph, adjacent_vertice, used, result);
        }
    }
}

void Solve(const Graph& graph,
           const int from,
           std::vector<int>& result)
{
    std::vector<bool> used(graph.size(), false);
    DFS(graph, from, used, result);
}

int main() {
    int vertices, edges;
    std::cin >> vertices >> edges;

    Graph graph(vertices + 1);

    for (int edge = 0; edge < edges; ++edge) {
        int from, to;
        std::cin >> from >> to;
        graph[from].push_back(to);
    }

    int reset_vertice;
    std::cin >> reset_vertice;

    std::vector<int> result;

    Solve(graph, reset_vertice, result);

    for (std::vector<int>::const_iterator it = result.begin();
         it != result.end();
         ++it)
    {
        std::cout << *it << " ";
    }
    std::cout << std::endl;

    return 0;
}

Теперь мы знаем, как сформировать множество вершин, составляющих ответ, но не знаем, как его упорядочить. Рассмотрим пример: пусть от подзадачи $A$ зависят подзадачи $B$ и $C$. В таком случае нам неважно, в каком порядке запускать подзадачи $B$ и $C$. Но что, если между ними существует явная или неявная (через другие подзадачи) зависимость?

Яндекс.Блиц. Почему и какие алгоритмические задачи нужно уметь решать, работая в поиске - 12

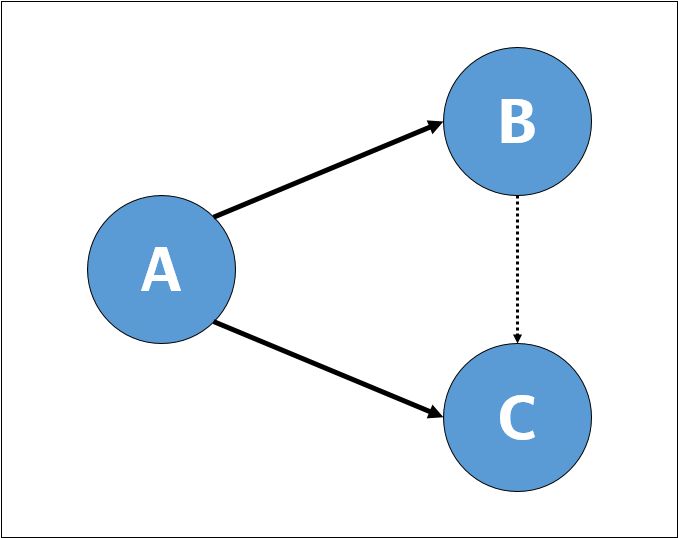
В ситуации, изображённой на картинке, сначала нужно исполнять задачу $B$, а уже потом $C$. Но стандартные методы обхода не позволяют этого добиться. Нам нужен другой алгоритм!

Используем для решения возникшей проблемы топологическую сортировку вершин, входящих в ответ, то есть, введём некоторый порядок на этом множестве вершин, например: $v_1$, $v_2$,...,$v_k$, и при этом будет верно, что, если $j > i$, то $v_j$ не зависит прямо или косвенно от $v_i$. Известно, что такое упорядочение возможно, если граф не содержит циклов. Топологическая сортировка вершин достигается при помощи обхода в глубину: когда для некоторой вершины посещены все её потомки, она добавляется в начало списка. Итоговый список будет искомой сортировкой вершин графа.

Таким образом, поставленная задача решается при помощи обхода в глубину, в процессе которого мы одновременно строим множество вершин, представляющих ответ, и осуществляем топологическую сортировку этих вершин. Топологическая сортировка гарантирует, что соответствующие вершинам графа подзадачи перечислены в правильном порядке.

Так будет выглядеть полное решение нашей задачи

#include <iostream>
#include <vector>

using Graph = std::vector<std::vector<int>>;

void DFS(const Graph& graph,
         const int vertice,
         std::vector<bool>& used,
         std::vector<int>& result)
{
    used[vertice] = true;
    for (size_t idx = 0; idx < graph[vertice].size(); ++idx) {
        const int adjacent_vertice = graph[vertice][idx];
        if (!used[adjacent_vertice]) {
            DFS(graph, adjacent_vertice, used, result);
        }
    }
    result.push_back(vertice);
}

void Solve(const Graph& graph,
           const int from,
           std::vector<int>& result)
{
    std::vector<bool> used(graph.size(), false);
    DFS(graph, from, used, result);
}

int main() {
    int vertices, edges;
    std::cin >> vertices >> edges;

    Graph graph(vertices + 1);

    for (int edge = 0; edge < edges; ++edge) {
        int from, to;
        std::cin >> from >> to;
        graph[from].push_back(to);
    }

    int reset_vertice;
    std::cin >> reset_vertice;

    std::vector<int> result;

    Solve(graph, reset_vertice, result);

    for (std::vector<int>::const_reverse_iterator it = result.rbegin();
         it != result.rend();
         ++it)
    {
        std::cout << *it << " ";
    }
    std::cout << std::endl;

    return 0;
}

2. Количество различных бинарных деревьев поиска

Эта задача не имеет непосредственного отношения к библиотекам и программам, разрабатываемым в Яндексе, зато она очень интересная и поэтому часто становится темой для обсуждений на кофепоинтах в свободную минуту. Она является несколько упрощённой версией задачи 9D с codeforces.

2.1. Постановка задачи

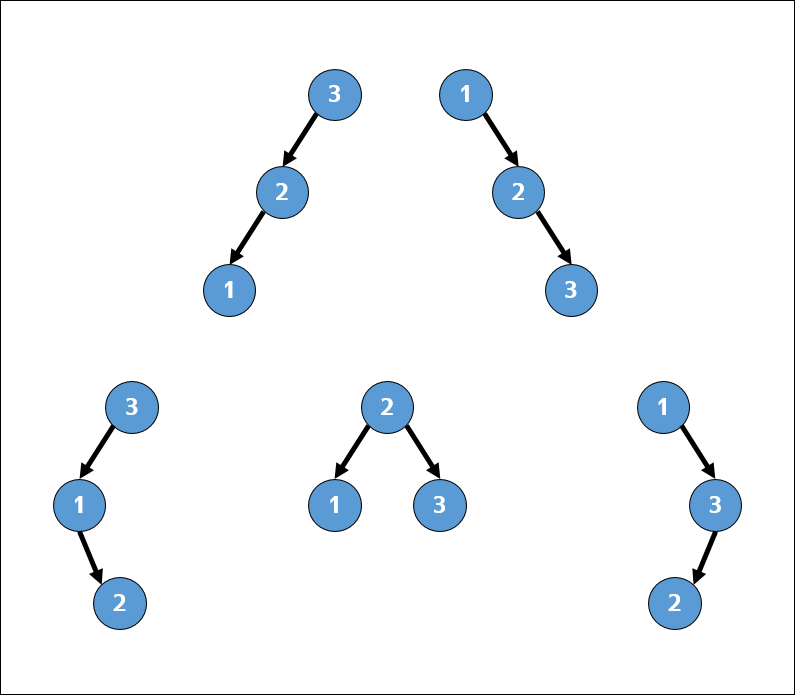
Необходимо вычислить, каково количество различных бинарных деревьев поиска, в вершинах которых записаны числа от 1 до $N$. Например, если $N=3$, существует ровно пять различных деревьев, изображённых на картинке ниже:

Яндекс.Блиц. Почему и какие алгоритмические задачи нужно уметь решать, работая в поиске - 23

Если $N=5$, то количество деревьев равняется 42. Именно поэтому задача очень нравится нашим разработчикам, среди которых немало ценителей творчества Дугласа Адамса.

2.2. Решение с использованием динамического программирования

Эта задача является достаточно простой для тех, кто знаком с методами динамического программирования. Обозначим за $T_k$ количество различных бинарных деревьев поиска, образованных числами $1$, $2$, ..., $K$. Предположим, что мы знаем $T_0$, $T_1$, $T_2$, ..., $T_N$ и хотим вычислить $T_{N+1}$.

Ясно, что в корне любого дерева будет находиться некоторое число из множества ${1,...,N+1.}$ Обозначим это число за $ t$. Тогда в силу свойств дерева поиска левое поддерево содержит числа $1,...,t-1$, а правое — ${t+1,...,N+1}$. Количество различных возможных способов сформировать левое поддерево тогда равняется $T_{t-1}$, а правое — $T_{N - t + 1}$. Поэтому общее количество деревьев, составленных из чисел $1$, $2$, ..., $N + 1$ и имеющих в корне значение $t$, равняется произведению $T_{i-1}cdot T_{N - t + 1}$. Для того, чтобы найти общее количество деревьев, необходимо просуммировать это произведение для всех возможных значений $t$:

$T_{N+1}=sum_{t=1}^{N+1} T_{i-1} cdot T_{N - t + 1}=sum_{t=0}^{N} T_{i} cdot T_{N - t}$

Приведем пример реализации, для разнообразия на языке программирования Python

N = int(raw_input())

result = [1, 1]

for count in xrange(2, N + 1):
    result.append(0)
    for root in xrange(1, count + 1):
        result[-1] += result[root - 1] * result[count - root]

print result[N]

2.3. Связь с числами Каталана

Задачу можно решить с использованием полученной формулы. Однако те, кому хорошо знакома комбинаторика, могли бы узнать в этом выражении формулу для вычисления чисел Каталана. Поэтому можно для получения ответа использовать формулу с использованием биномиальных коэффициентов:

$T_{N+1}=C_{N+1}=frac{C_{2N + 2}^{N+1} }{N + 2}$

В процессе решения задачи про бинарные деревья мы получили рекуррентную формулу, полностью аналогичную рекуррентной формуле, возникающей при решении задачи про количество правильных скобочных последовательностей длины $2N$, которая, как правило, и используется для введения чисел Каталана в курсах по комбинаторике.

Яндекс.Блиц будет проходить на платформе Контест, где мы обычно проводим Алгоритм. Для участия нужно зарегистрироваться. Мы обязательно пришлём вам напоминание о старте раундов.

Автор: Никита Макаров

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js