Один мой друг любит говорить (не знаю, его это слова или он их где-то взял), что в программисты идут по двум причинам: если ты хочешь стать хакером или если ты хочешь писать игры. Мой случай второй. Всегда интересовался разработкой игр, причём той частью, которая отвечает за искусственный интеллект в играх. Очень много времени я потратил на изучение алгоритмов поиска пути. Реализуя очередную версию алгоритма A* на Java, столкнулся с интересной ситуацией, связанной с коллекциями TreeSet и TreeMap.
Сразу хочу ввести два понятия, которые буду использовать на протяжении всей статьи: поиск по равенству и поиск по сравнению. Поиском по равенству я буду называть поиск в коллекции, где для сравнения элементов используются методы equals и hashCode. Поиском по сравнению или поиском на основании сравнения я буду называть поиск элемента в коллекции, где для сравнения элементов используются методы compare и compareTo.
В алгоритме A* используется две коллекции для хранения точек пути: открытый список и закрытый список. Точка пути, грубо говоря, имеет для нас три важных атрибута: координату X, координату Y и значение метрической функции – F. Для закрытого списка необходимо выполнять только две операции добавление и поиск. С открытым списком всё несколько сложней. С открытым списком помимо операций добавления и поиска элемента необходимо также находить наименьшую точку по значению метрической функции.
Для закрытого списка выбираем HashSet тут всё очевидно, для операций добавления и поиска отлично подходит, если конечно вы написали хорошую хэш-функцию. С выбором коллекции для закрытого списка возникают затруднения. Если выбрать HashSet, как и для закрытого списка, то мы получим наилучшую асимптотику для операций вставки, поиска и удаления – O(1), однако поиск минимального будет выполняться за O(n). При выборе TreeSet или TreeMap мы будем иметь O(log(n)) для вставки и поиска, но для поиска и удаления минимального будем иметь всего лишь O(1). Посмотреть асимптотики различных коллекций можно тут.
Ещё одна важная деталь, связанная с TreeMap и TreeSet – все операции с этими коллекциями используют сравнения. Таким образом, если поиск нас интересует с учётом координат точек, то для поиска минимального мы используем значение метрической функции, а это приведёт к тому, что операция может быть не выполнена для точки, у которой изменили это значение. Более того при вставке новых значений мы можем получить некорректно построенное дерево: если считать точки с одинаковыми координатами равными и учесть это в компараторе, то вставка нового значения в дерево не произойдёт.
Имеет смысл использовать коллекцию на основе бинарного дерева, так как элементы в открытый список добавляются не так часто, в то время как поиск минимального элемента по значению метрической функции выполняется на каждой итерации поискового алгоритма. Это связано с тем, что добавление в открытый список зависит от наличия аналогичного (по координатам) элемента в закрытом списке, который со временем растёт и в нём оказывается всё большее количество точек – чем больше точек в закрытом списке, тем меньше вероятность добавления элемента в открытый список. Но также хотелось бы иметь преимущества коллекции HashSet.
Я решил обобщить задачу. Пусть определена некоторая структура данных, в которой имеется набор полей. Пусть также некоторые поля определяют отношение эквивалентности двух элементов данной структуры, в то время как другие поля определяют отношения порядка (проще говоря, методы equals и hashCode используют одни поля объекта, а методы compare и compareTo другие).
Задача: реализовать структуру данных, в которой операция поиска элемента на основании равенства выполняется с асимптотикой O(1), а операции вставки и удаления работали с учётом операций и сравнения и равенства, и строили бинарное дерево таким образом, что наименьший элемент был бы корнем дерева.
Так как для моих целей мне нужно хранить в открытом списке точки с учётом их координат, то я могу однозначно определить хэш-функцию на основании размера карты проходимости так, что в ней будут отсутствовать коллизии, поэтому я и в коллекции решил задать константой максимальное количество элементов.
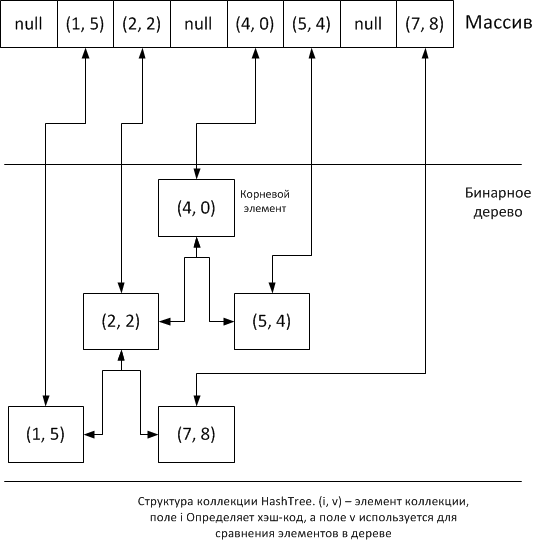
Идея очень проста: будем помещать на основании хеширования элементы коллекции в массив, и тут же помещать эти же элементы в бинарное дерево. Нам понадобиться внутренний класс для упаковки элементов в узлы дерева:
private static class Node<V extends Comparable<V>> {
private Node parent;
private Node left;
private Node right;
private final V data;
public Node(V data) {
this.data = data;
this.parent = null;
this.left = null;
this.right = null;
}
}
Тип V определяет элемент коллекции, он должен расширять класс Comparable, чтобы можно было выполнять сравнение для построения дерева.
В классе помимо указателей на левого и правого потомка есть указатель на предка. Это сделано для оптимизации процесса удаления элемента из дерева – имея прародителя удаляемого элемента можно исключить из алгоритма удаления обход дерева начиная с корня, для поиска можно будет воспользоваться массивом элементов.
Внутри коллекции должен быть указатель на корень дерева и массив элементов коллекции, где в пустых ячейках хранится null, а в заполненных экземпляры класса Node, где в поле data будет храниться значение добавленного элемента (а точнее значение указателя на экземпляр объекта):
public abstract class HashTree<E extends Comparable<E>> {
private Node root = null;
private Node[] nodes;
public HashTree(int capacity) {
this.nodes = new Node[capacity];
}
public abstract int getElementHash(E element);
…
}Как и тип V, тип E определяет элемент коллекции. По умолчанию коллекция пуста, поэтому указатель на корневой элемент – null и массив также заполнен значениями null. Класс абстрактный с абстрактным методом getElementHash, позволяющим переопределить вычисление хэш-кода.
Теперь к методам. Метод addElement:
public void addElement(E element) {
int index = getElementHash(element);
if (nodes[index] != null) {
return;
}
Node<E> node = new Node<>(element);
nodes[index] = node;
this.root = connectNodes(this.root, node);
}В методе получаем хэш-код добавляемого элемента. Создаём новый узел дерева с новым элементом в качестве данных и добавляем его в дерево и в массив, где хэш-код определяет индекс в массиве. Вставка элемента в массив имеет асимптотику O(1), вставка в дерево — O(log(n)), суммарная асимптотика – O(log(n)).
Метод removeElement:
public E removeElement(E element) {
int index = getElementHash(element);
Node node = nodes[index];
if (node == null) {
return null;
}
nodes[index] = null;
E data = (E) node.data;
Node l = getElemInArray(node.left);
Node r = getElemInArray(node.right);
l = connectNodes(l, r);
if (node.parent == null) {
this.root = l;
if (this.root != null) {
this.root.parent = null;
}
return data;
}
int p = getElementHash((E) node.parent.data);
if (nodes[p] != null && nodes[p].left == node)
nodes[p].left = null;
}
connectNodes(nodes[p], l);
return data;
}Здесь, используя хэш-код удаляемого элемента, извлекается из массива узел дерева, который нужно удалить. Используя предка удаляемого узла, выполняем удаление элемента, в процессе которого приходится 2 раза вызывать связывание поддеревьев, каждая из операций в худшем случае обладают асимптотикой – O(log(n)). В итоге метод имеет асимптотику O(log(n)).
Метод connectNodes выполняет присоединение, как одиночного узла, так и поддерева. Причём связывание происходит с применением сравнения. Таким образом, в вершине дерева всегда находится наименьший элемент.
Метод connectNodes:
private Node connectNodes(Node parent, Node node) {
if (parent == null) {
return node;
} else if (compare(node, parent) < 0) {
node.left = parent;
parent.parent = node;
parent = node;
return parent;
} else {
Node cur = parent;
Node n = node;
while (cur != null) {
if (compare(n, cur.left) < 0) {
if (cur.right == null) {
cur.right = cur.left;
cur.left = n;
n.parent = cur;
break;
}
Node tmp = cur.left;
cur.left = n;
n.parent = cur;
cur = n;
n = tmp;
continue;
}
if (compare(n, cur.right) < 0
&& compare(n, cur.left) > 0) {
Node tmp = cur.right;
cur.right = n;
n.parent = cur;
cur = n;
n = tmp;
continue;
}
if (compare(n, cur.right) > 0) {
cur = cur.left;
}
}
return parent;
}
}Поиск элемента можно осуществлять не в дереве, а в массиве на основании хэш-кода, поэтому операция поиска имеет асимптотику O(1). А так как дерево организовано как бинарное, то в корне всегда находится минимальный элемент по сравнению и асимптотика поиска минимального — O(1). Замечу, что удаление минимального элементы имеет асимптотику O(log(n)), так как при удалении требуется реорганизовать дерево, начиная с корня.
На первый взгляд операция удаления минимального элемента в реализованной коллекции имеет худшую асимптотику, чем у коллекции HashSet, но не стоит забывать, что прежде чем удалить минимальный элемент его сначала нужно найти, а для этого требуется выполнить операции с асимптотикой O(n). Таким образом, итоговая асимптотика операции удаления минимального элемента в коллекции HashSet будет иметь вид –O(n).
Проверка наличия элемента в коллекции, как уже говорилось выше, выполняется на основании проверки на null элемента массива по индексу, определяемому хэш-кодом элемента. Проверка выполняется методом contains и имеет асимптотику O(1):
public boolean contains(E element) {
int index = getElementHash(element);
return nodes[index] != null;
} Также на основании хэш-кода выполняется поиск по равенству при чём с той же асимптотикой при помощи метода getElement:
public E getElement(E element) {
return (E) nodes[getElementHash(element)].data;
}Реализованная коллекция не лишена недостатков. Она требует больше памяти, ей нужна хэш-функция без коллизий и для реализации перебора элементов придётся реализовывать обход дерева, что также не доставляет удовольствия, но данная коллекция предназначена для других целей. Главное преимущество – это возможность поиска элементов одного типа по разным критериям с наилучшей асимптотикой. В применении к моей задаче, это был поиск по равенству на основании координат и поиск минимального элемента на основании сравнения значений метрической функции.
В конце приведу результаты тестирования коллекции на быстродействие по сравнению с коллекциями LinkedHashMap, TreeSet и HashSet. Все коллекции заполнялись 1000 значений типа Integer и, с заполненными коллекциями, проводился следующий набор операций:
- помещение нового элемента в коллекцию;
- проверка на наличие в коллекции элемента с заданным значением (проверка выполнялась дважды для элемента, который был в коллекции и для элемента, которого в коллекции не было);
- поиск и удаление минимально по сравнения элемента;
- удаление, добавленного в пункте 1, элемента.
Результаты тестов приведены в таблице:
| Коллекция | Количество повторений | Затраченное время |
|---|---|---|
| LinkedHashMap | 10 000 000 | 1985±90 мс |
| TreeSet | 10 000 000 | 1190±25 мс |
| HashSet | 1 000 000 | 4350±100 мс |
| HashTree | 10 000 000 | 935±25 мс |
В итоге имеем более чем в 2 раза большую скорость коллекции HashTree по сравнению с LinkedHashMap и в 1.27 раза большую по сравнению с TreeSet (рассматривать HashSet не имеет смысла вообще). Проверки выполнялись на машине с 4Гб оперативной памяти и процессором AMD Phenom(tm)II X4 940, ОС – 32-разрядная Windows7 Профессиональная.
P.S.: Коллекцию можно ещё больше ускорить за счёт использования красно-чёрного дерева вместо бинарного.
Автор: soulYangor




