Стрелки как подход к представлению систем на Java

Часто встречается описание систем, алгоритмов и процессов в виде структурных схем. Следовательно, актуальна задача представления структурных схем, к примеру, из технической документации или спецификации, на языке программирования.

В статье рассматривается подход к представлению структурных схем с использованием концепции стрелок (arrows), описанных Джоном Хьюзом и нашедших применение в Haskell в FRP-фреймворках Yampa и Netwire, а также в XML-фреймворке Haskell XML Toolbox.

Особенностью структурных схем является наглядное представление последовательностей операций (блоков) без акцентирования внимания на самих обрабатываемых данных (переменных) и их состояниях. Для примера рассмотрим радиоприёмник прямого усиления

Как же реализовать такой способ описания систем и вычислений в рамках существующих мейнстримовых языков программирования?

Традиционное описание такой схемы на C-подобном языке программирования выглядело бы примерно так

// Создаём блоки обработки
Antenna antenna = new Antenna(Ether.getInstance());
Filter filter1 = new Filter(5000);      // параметр - частота настройки
Filter filter2 = new Filter(5000);
Filter filter3 = new Filter(5000);

Detector detector = new Detector("AM"); // тип модуляции - амплитудная
Amplifier amp = new Amplifier(5);       // коэффициент усиления
Speaker speaker = new Speaker(10);      // громкость

Signal inputSignal = antenna.receive();

# Описываем связи между блоками
Signal filter1Res = filter1.filter(inputSignal);
Signal filter2Res = filter2.filter(filter1Res);
Signal filter3Res = filter3.filter(filter2Res);
Signal detected = detector.detect(filter3Res);
Signal amplified = amp.amplify(detected);

speaker.speak(amplified);

Видно, что в программу добавились переменные, которых нет в структурной схеме, и которые, следовательно, не добавляют никакой информации о работе радиоприёмника, а нужны лишь для хранения промежуточных результатов обработки входного сигнала.

Такая программа, описывающая лишь простое поэтапное прохождение сигнала через блоки обработки, выглядит довольно громоздко. Более лаконичным подходом будет описание схемы с использованием нового метода join, подключающего блоки друг к другу:

Receiver receiver = Receiver.join(filter1).join(filter2).join(filter3)
    .join(detector).join(amp).join(speaker);

receiver.apply(antenna.receive());

Метод join() описывает последовательное соединение блоков, то есть a.join(b) означает, что результат обработки блоком a будет передан на вход блока b. При этом лишь требуется, чтобы соединяемые классы Filter, Amplifier, Detector, Speaker дополнительно реализовывали метод apply(), выполняющий "действие по умолчанию" (для фильтра Filter — filter(), для Amplifier — amplify() и т. д.) и позволяющий вызывать объект как функцию.

При функциональном подходе эти классы были бы функциями, возвращающими функции, так что нам не пришлось бы даже создавать экземпляры классов и вся программа выглядела бы примерно так:

Receiver receiver = Receiver.join(filter(5000)).join(filter(5000)).join(filter(5000))
    .join(detector("AM")).join(amplifier(5)).join(speaker(10));

receiver.apply(antenna.receive());

Стрелки как способ описания вычислений

Особенностью функционального подхода является использование комбинаторов (например монад), которые являются функциями, объединяющими другие функции в составные вычисления.

Стрелки (arrows) также являются комбинатором и позволяют обобщенно описывать составные вычисления. В этой статье используется реализация стрелок jArrows, написанная на Java 8.

Что такое стрелка

Стрелка Arrow<In, Out> a от функции Out f(In x) представляет вычисление, которое выполняется функцией f. Как вы уже могли догадаться In — тип входного значения стрелки (принимаемого функцией f), Out — тип выходного значения (возвращаемого функцией f). Преимуществом представления вычислений в виде стрелок является возможность явного комбинирования вычислений различными способами.

Например вычисление y = x * 5.0, на Java представленное функцией

double multBy5_0(int in) { 
    return in*5.0; 
}

можно представить в виде стрелки

Arrow<Integer, Double> arrMultBy5_0 = Action.of(multBy5_0);

Далее упакованное в стрелку вычисление можно комбинировать с другими вычислениями-стрелками. Класс Action является одной из реализаций интерфейса Arrow. Другой реализацией этого интерфейса является ParallelAction, поддерживающий многопоточные вычисления.

Композиция стрелок

Стрелку arrMultBy5_0 можно последовательно соединить с другой стрелкой — например, прибавляющей к входному значению 10.5, а затем — со следующей стрелкой, представляющей результат в виде строки. Получится цепочка из стрелок

Arrow<Integer, String> mult5Plus10toStr = arrMultBy5_0.join(in -> in+10.5)
                                                      .join(in -> String.valueOf(in));
mult5Plus10toStr.apply(10);      //  "60.5"                  

Получившееся вычисление, представленное составной стрелкой mult5Plus10toStr, можно представить в виде структурной схемы:

Вход этой стрелки имеет тип Integer (входной тип первого вычисления в цепочке), а выход имеет тип String (выходной тип последнего вычисления в цепочке).

Метод someArrow.join(g) соединяет в цепочку вычисление, представленное стрелкой someArrow с вычислением, представленным g, при этом g может быть другой стрелкой, лямбда-функцией, методом, или чем-то ещё, что реализует интерфейс Applicable с методом apply(x), который можно применить к входному значению x.

class Action<In, Out> implements Arrow<In, Out>, Applicable<In, Out> {
    Applicable<In, Out> func;

    public Arrow<In, OutB> join(Applicable<Out, OutB> b) {
        return Action.of(i -> b.apply(this.func.apply(i)));
    }
}

Другие способы композиции стрелок

Кроме последовательного соединения методом join стрелки можно соединять параллельно методами combine, cloneInput и split. Пример использования метода combine для описания вычисления sin(x)^2+cos(x)^2

Arrow<Pair<Double, Double>, Pair<Double, Double>> 
    sin_cos = Action.of(Math::sin).combine(Math::cos);

Arrow<Double, Double> sqr = Action.of(i -> i*i);

Arrow<Pair<Double, Double>, Double> sum_SinCos = sin_cos.join(sqr.combine(sqr))
                            .join(p -> p.left + p.right);

sum_SinCos.apply(Pair.of(0.7, 0.2));    // 1.38

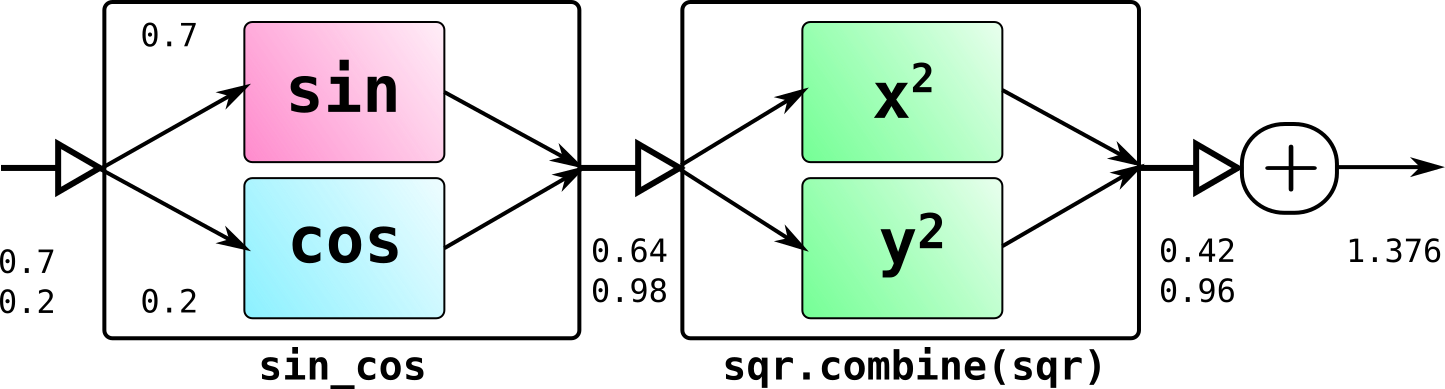
Получившаяся "широкая" стрелка sin_cos принимает на вход пару значений типа Pair<Double, Double>, первое значение pair.left пары попадает на вход первой стрелки (функция sin), второе pair.right — на вход второй стрелки (функция cos), их результаты тоже объединяются в пару. Следующая составная стрелка sqr.combine(sqr) принимает на вход значение типа Pair<Double, Double>и возводит оба значения пары в квадрат. Последняя стрелка суммирует результат.

Метод someArrow.cloneInput(f) создаёт стрелку, параллельно соединяя someArrow и f и применяя их к входу, её выход представляется в виде пары, объединяющей результаты вычилений этих стрелок. Входные типы someArrow и f должны совпадать.

Arrow<Integer, Pair<Integer, Double>> sqrAndSqrt = Action.of((Integer i) -> i*i)
                            .cloneInput(Math::sqrt); 
sqrAndSqrt.apply(5);  // Pair(25, 2.236)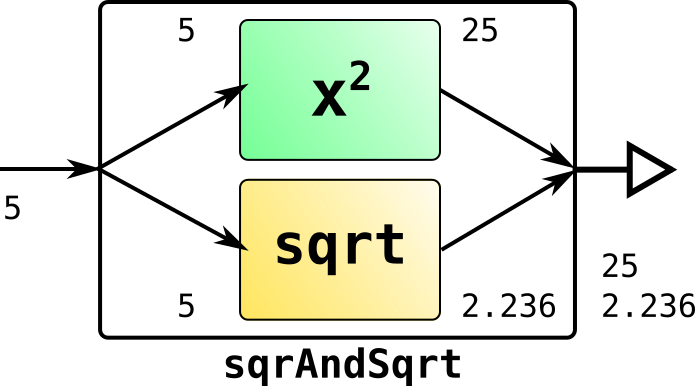

Параллельное соединение в данном случае означает, что результаты двух вычислений, соединённых параллельно, не зависят друг от друга — в отличии от последовательного соединения методом join, когда результат одного вычисления передаётся на вход другого. Многопоточные параллельные соединения реализуется классом ParallelAction.

Метод someArrow.split(f, g) — дополнительный метод, эквивалентный someArrow.join(f.cloneInput(g)). Результат вычисления someArrow параллельно передаётся на вход f и g, выходом такой стрелки будет пара с результатами вычислений f и g.

Обход вычислений

Иногда нужно передать часть входного значения стрелки далее по цепочке вместе с результатом вычисления. Это реализуется методом someArrow.first() и дополняющим его someArrow.second(), преобразующим стрелку someArrow так, что получившаяся стрелка принимает на вход пару значений и применяет вычисление лишь к одному из элементов этой пары

Arrow<Integer, Double> arr = Action.of(i -> Math.sqrt(i*i*i));

Pair input = Pair.of(10, 10);

arr.<Integer>first().apply(Pair.of(10, 10)));     // Pair(31.623, 10)
arr.<Integer>second().apply(Pair.of(10, 10)));    // Pair(10, 31.623)

Эти методы аналогичны методам someArrow.bypass2nd() и someArrow.bypass1st() соответственно.

Полнота описания

Согласно Хьюзу, описание любого вычисления возможно с использованием лишь трёх функций:

• 1) Конструктора, строящего стрелку из функции (в данной реализации Action.of)
• 2) Функции, последовательно соединяющей две стрелки (Arrow::join)
• 2) Функции, применяющей вычисление к части входа (Arrow::first)

Реализация jArrows также расширена дополнительными методами, упрощающими описание систем.

Выводы

Высокоуровневое описание процессов в виде блок-схем практически не используется в императивном подходе в программировании. В тоже время такое описание хорошо укладывается в функциональный реактивный подход, получающий всё большее распространение.

Как показано в статье Хьюза, стрелки, по-сути являющиеся реализацией описания систем в виде блок-схем в рамках функционального программирования, являются более обобщенным описанием, чем монады, которые уже получили распространение в мейнстриме, в частности в виде их реализации Optional в Java 8. В данной статье описаны основные принципы данного подхода, в дальнейшем представляет интерес адаптация существующих и разработка новых паттернов для применения стрелок в мейнстримовой разработке программного обеспечения.

Автор: yarric

Источник