Здравствуй!
В этой статье речь пойдет о задачах на рекурсию и о том как их решать.

Кратко о рекурсии
Рекурсия достаточно распространённое явление, которое встречается не только в областях науки, но и в повседневной жизни. Например, эффект Дросте, треугольник Серпинского и т. д. Самый простой вариант увидеть рекурсию – это навести Web-камеру на экран монитора компьютера, естественно, предварительно её включив. Таким образом, камера будет записывать изображение экрана компьютера, и выводить его же на этот экран, получится что-то вроде замкнутого цикла. В итоге мы будем наблюдать нечто похожее на тоннель.
В программировании рекурсия тесно связана с функциями, точнее именно благодаря функциям в программировании существует такое понятие как рекурсия или рекурсивная функция. Простыми словами, рекурсия – определение части функции (метода) через саму себя, то есть это функция, которая вызывает саму себя, непосредственно (в своём теле) или косвенно (через другую функцию).
О рекурсии сказано много. Вот несколько хороших ресурсов:
- с хабра
- wikipedia
- wikibooks
- Рекурсия и рекурсивные задачи. Области применение рекурсии
- Рекурсивные алгоритмы. Области применение рекурсии
- О пользе рекурсии
- Заметки о рекурсии
- Заметки о рекурсии — 2. Взгляд на рекурсию изнутри
Предполагается что читатель теоритически знаком с рекурсией и знает что это такое. В данной статье мы бóльшее вниманиее уделим задачам на рекурсию.
Задачи
При изучении рекурсии наиболее эффективным для понимания рекурсии является решение задач.
Как же решать задачи на рекурсию ?
В первую очередь надо понимать что рекурсия это своего рода перебор. Вообще говоря, всё то, что решается итеративно можно решить рекурсивно, то есть с использованием рекурсивной функции.
Для обоснования можно привести такие доводы.
Для начала можно вспомнить определение рекурсии и итерации. Рекурсия — это такой способ организации обработки данных, при котором программа вызывает сама себя непосредственно, либо с помощью других программ. Итерация — это способ организации обработки данных, при котором определенные действия повторяются многократно, не приводя при этом к рекурсивным вызовам программ.
После чего можно сделать вывод, что они взаимно заменимы, но не всегда с одинаковыми затратами по ресурсам и скорости. Для обоснования можно привести такой пример: имеется функция, в которой для организации некого алгоритма имеется цикл, выполняющий последовательность действий в зависимости от текущего значения счетчика (может от него и не зависеть). Раз имеется цикл, значит, в теле повторяется последовательность действий — итерации цикла. Можно вынести операции в отдельную подпрограмму и передавать ей значение счетчика, если таковое есть. По завершению выполнения подпрограммы мы проверяем условия выполнения цикла, и если оно верно, переходим к новому вызову подпрограммы, если ложно — завершаем выполнение. Т.к. все содержание цикла мы поместили в подпрограмму, значит, условие на выполнение цикла помещено также в подпрограмму, и получить его можно через возвращающее значение функции, параметры передающееся по ссылке или указателю в подпрограмму, а также глобальные переменные. Далее легко показать, что вызов данной подпрограммы из цикла легко переделать на вызов, или не вызов (возврата значения или просто завершения работы) подпрограммы из нее самой, руководствуясь какими-либо условиями (теми, что раньше были в условии цикла). Теперь, если посмотреть на нашу абстрактную программу, она примерно выглядит как передача значений подпрограмме и их использование, которые изменит подпрограмма по завершению, т.е. мы заменили итеративный цикл на рекурсивный вызов подпрограммы для решения данного алгоритма.
Задача по приведению рекурсии к итеративному подходу симметрична.
Подводя итог, можно выразить такие мысли: для каждого подхода существует свой класс задач, который определяется по конкретным требованиям к конкретной задаче.
Более подробно с этим можно познакомиться тут
Так же как и у перебора (цикла) у рекурсии должно быть условие остановки — Базовый случай (иначе также как и цикл рекурсия будет работать вечно — infinite). Это условие и является тем случаем к которому рекурсия идет (шаг рекурсии). При каждом шаге вызывается рекурсивная функция до тех пор пока при следующем вызове не сработает базовое условие и произойдет остановка рекурсии(а точнее возврат к последнему вызову функции). Всё решение сводится к решению базового случая. В случае, когда рекурсивная функция вызывается для решения сложной задачи (не базового случая) выполняется некоторое количество рекурсивных вызовов или шагов, с целью сведения задачи к более простой. И так до тех пор пока не получим базовое решение.
Итак рекурсивная функция состоит из
- Условие остановки или же Базовый случай
- Условие продолжения или Шаг рекурсии — способ сведения задачи к более простым.
Рассмотрим это на примере нахождения факториала:
public class Solution {
public static int recursion(int n) {
// условие выхода
// Базовый случай
// когда остановиться повторять рекурсию ?
if (n == 1) {
return 1;
}
// Шаг рекурсии / рекурсивное условие
return recursion(n - 1) * n;
}
public static void main(String[] args) {
System.out.println(recursion(5)); // вызов рекурсивной функции
}
}
Тут Базовым условием является условие когда n=1. Так как мы знаем что 1!=1 и для вычисления 1! нам ни чего не нужно. Чтобы вычислить 2! мы можем использовать 1!, т.е. 2!=1!*2. Чтобы вычислить 3! нам нужно 2!*3… Чтобы вычислить n! нам нужно (n-1)!*n. Это и является шагом рекурсии. Иными словами, чтобы получить значение факториала от числа n, достаточно умножить на n значение факториала от предыдущего числа.
В сети при обьяснении рекурсии также даются задачи нахождения чисел Фибоначчи и Ханойская башня
Рассмотрим же теперь задачи с различным уровнем сложности.
Попробуйте их решить самостоятельно используя метод описанный выше. При решении попробуйте думать рекурсивно. Какой базовый случай в задаче? Какой Шаг рекурсии или рекурсивное условие?
Поехали! Решения задач предоставлены на языке Java.
A: От 1 до n
Дано натуральное число n. Выведите все числа от 1 до n.
public class Solution {
public static String recursion(int n) {
// Базовый случай
if (n == 1) {
return "1";
}
// Шаг рекурсии / рекурсивное условие
return recursion(n - 1) + " " + n;
}
public static void main(String[] args) {
System.out.println(recursion(10)); // вызов рекурсивной функции
}
}
B: От A до B
Даны два целых числа A и В (каждое в отдельной строке). Выведите все числа от A до B включительно, в порядке возрастания, если A < B, или в порядке убывания в противном случае.
public class Solution {
public static String recursion(int a, int b) {
// основное условие задачи
if (a > b) {
// Базовый случай
if (a == b) {
return Integer.toString(a);
}
// Шаг рекурсии / рекурсивное условие
return a + " " + recursion(a - 1, b);
} else {
// Базовый случай
if (a == b) {
return Integer.toString(a);
}
// Шаг рекурсии / рекурсивное условие
return a + " " + recursion(a + 1, b);
}
}
public static void main(String[] args) {
System.out.println(recursion(20, 15)); // вызов рекурсивной функции
System.out.println(recursion(10, 15)); // вызов рекурсивной функции
}
}
C: Функция Аккермана
В теории вычислимости важную роль играет функция Аккермана A(m,n), определенная следующим образом:
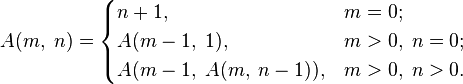
Даны два целых неотрицательных числа m и n, каждое в отдельной строке. Выведите A(m,n).
public class Solution {
public static int recursion(int m, int n) {
// Базовый случай
if (m == 0) {
return n + 1;
} // Шаг рекурсии / рекурсивное условие
else if (n == 0 && m > 0) {
return recursion(m - 1, 1);
} // Шаг рекурсии / рекурсивное условие
else {
return recursion(m - 1, recursion(m, n - 1));
}
}
public static void main(String[] args) {
System.out.println(recursion(3, 2)); // вызов рекурсивной функции
}
}
D: Точная степень двойки
Дано натуральное число N. Выведите слово YES, если число N является точной степенью двойки, или слово NO в противном случае.
Операцией возведения в степень пользоваться нельзя!
public class Solution {
public static int recursion(double n) {
// Базовый случай
if (n == 1) {
return 1;
} // Базовый случай
else if (n > 1 && n < 2) {
return 0;
} // Шаг рекурсии / рекурсивное условие
else {
return recursion(n / 2);
}
}
public static void main(String[] args) {
double n = 64;
// вызов рекурсивной функции
if (recursion(n) == 1) {
System.out.println("Yes");
} else {
System.out.println("No");
}
}
}
E: Сумма цифр числа
Дано натуральное число N. Вычислите сумму его цифр.
При решении этой задачи нельзя использовать строки, списки, массивы (ну и циклы, разумеется).
public class Solution {
public static int recursion(int n) {
// Базовый случай
if (n < 10) {
return n;
}// Шаг рекурсии / рекурсивное условие
else {
return n % 10 + recursion(n / 10);
}
}
public static void main(String[] args) {
System.out.println(recursion(123)); // вызов рекурсивной функции
}
}
F: Цифры числа справа налево
Дано натуральное число N. Выведите все его цифры по одной, в обратном порядке, разделяя их пробелами или новыми строками.
При решении этой задачи нельзя использовать строки, списки, массивы (ну и циклы, разумеется). Разрешена только рекурсия и целочисленная арифметика.
public class Solution {
public static int recursion(int n) {
// Базовый случай
if (n < 10) {
return n;
}// Шаг рекурсии / рекурсивное условие
else {
System.out.print(n % 10 + " ");
return recursion(n / 10);
}
}
public static void main(String[] args) {
System.out.println(recursion(123)); // вызов рекурсивной функции
}
}
G: Цифры числа слева направо
Дано натуральное число N. Выведите все его цифры по одной, в обычном порядке, разделяя их пробелами или новыми строками.
При решении этой задачи нельзя использовать строки, списки, массивы (ну и циклы, разумеется). Разрешена только рекурсия и целочисленная арифметика.
public class Solution {
public static String recursion(int n) {
// Базовый случай
if (n < 10) {
return Integer.toString(n);
} // Шаг рекурсии / рекурсивное условие
else {
return recursion(n / 10) + " " + n % 10;
}
}
public static void main(String[] args) {
System.out.println(recursion(153)); // вызов рекурсивной функции
}
}
H: Проверка числа на простоту
Дано натуральное число n>1. Проверьте, является ли оно простым. Программа должна вывести слово YES, если число простое и NO, если число составное. Алгоритм должен иметь сложность O(logn).
Указание. Понятно, что задача сама по себе нерекурсивна, т.к. проверка числа n на простоту никак не сводится к проверке на простоту меньших чисел. Поэтому нужно сделать еще один параметр рекурсии: делитель числа, и именно по этому параметру и делать рекурсию.
public class Solution {
public static boolean recursion(int n, int i) {
// i- дополнительный параметр. При вызове должен быть равен 2
// Базовый случай
if (n < 2) {
return false;
} // Базовый случай
else if (n == 2) {
return true;
} // Базовый случай
else if (n % i == 0) {
return false;
} // Шаг рекурсии / рекурсивное условие
else if (i < n / 2) {
return recursion(n, i + 1);
} else {
return true;
}
}
public static void main(String[] args) {
System.out.println(recursion(18, 2)); // вызов рекурсивной функции
}
}
I: Разложение на множители
Дано натуральное число n>1. Выведите все простые множители этого числа в порядке неубывания с учетом кратности. Алгоритм должен иметь сложность O(logn).
public class Solution {
public static void recursion(int n, int k) {
// k- дополнительный параметр. При вызове должен быть равен 2
// Базовый случай
if (k > n / 2) {
System.out.println(n);
return;
}
// Шаг рекурсии / рекурсивное условие
if (n % k == 0) {
System.out.println(k);
recursion(n / k, k);
} // Шаг рекурсии / рекурсивное условие
else {
recursion(n, ++k);
}
}
public static void main(String[] args) {
recursion(150, 2); // вызов рекурсивной функции
}
}
J: Палиндром
Дано слово, состоящее только из строчных латинских букв. Проверьте, является ли это слово палиндромом. Выведите YES или NO.
При решении этой задачи нельзя пользоваться циклами, в решениях на питоне нельзя использовать срезы с шагом, отличным от 1.
public class Solution {
public static String recursion(String s) {
// Базовый случай
if (s.length() == 1) {
return "YES";
} else {
if (s.substring(0, 1).equals(s.substring(s.length() - 1, s.length()))) {
// Базовый случай
if (s.length() == 2) {
return "YES";
}
// Шаг рекурсии / рекурсивное условие
return recursion(s.substring(1, s.length() - 1));
} else {
return "NO";
}
}
}
public static void main(String[] args) {
System.out.println(recursion("radar")); // вызов рекурсивной функции
}
}
K: Вывести нечетные числа последовательности
Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Выведите все нечетные числа из этой последовательности, сохраняя их порядок.
В этой задаче нельзя использовать глобальные переменные и передавать какие-либо параметры в рекурсивную функцию. Функция получает данные, считывая их с клавиатуры. Функция не возвращает значение, а сразу же выводит результат на экран. Основная программа должна состоять только из вызова этой функции.
public class Solution {
public static void recursion() {
java.util.Scanner in = new java.util.Scanner(System.in);
int n = in.nextInt();
// Базовый случай
if (n > 0) {
// Шаг рекурсии / рекурсивное условие
if (n % 2 == 1) {
System.out.println(n);
recursion();
} else {
recursion();
}
}
}
public static void main(String[] args) {
recursion(); // вызов рекурсивной функции
}
}
L: Вывести члены последовательности с нечетными номерами
Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Выведите первое, третье, пятое и т.д. из введенных чисел. Завершающий ноль выводить не надо.
В этой задаче нельзя использовать глобальные переменные и передавать какие-либо параметры в рекурсивную функцию. Функция получает данные, считывая их с клавиатуры. Функция не возвращает значение, а сразу же выводит результат на экран. Основная программа должна состоять только из вызова этой функции.
public class Solution {
public static void recursion() {
java.util.Scanner in = new java.util.Scanner(System.in);
int n = in.nextInt();
// Базовый случай
if (n > 0) {
int m = in.nextInt();
System.out.println(n);
// Базовый случай
if (m > 0) {
// Шаг рекурсии / рекурсивное условие
recursion();
}
}
}
public static void main(String[] args) {
recursion(); // вызов рекурсивной функции
}
}
M: Максимум последовательности
Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите наибольшее значение числа в этой последовательности.
В этой задаче нельзя использовать глобальные переменные и передавать какие-либо параметры в рекурсивную функцию. Функция получает данные, считывая их с клавиатуры. Функция возвращает единственное значение: максимум считанной последовательности. Гарантируется, что последовательность содержит хотя бы одно число (кроме нуля).
public class Solution {
public static int recursion() {
java.util.Scanner in = new java.util.Scanner(System.in);
int n = in.nextInt();
// Базовый случай
if (n == 0) {
return 0;
} // Шаг рекурсии / рекурсивное условие
else {
return Math.max(n, recursion());
}
}
public static void main(String[] args) {
System.out.println(recursion()); // вызов рекурсивной функции
}
}
N: Среднее значение последовательности
Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите среднее значение элементов этой последовательности (без учета последнего нуля).
В этой задаче нельзя использовать глобальные переменные. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметра. В программе на языке Python функция возвращает кортеж из пары чисел: число элементов в последовательности и их сумма. В программе на языке C++ результат записывается в две переменные, которые передаются в функцию по ссылке.
Гарантируется, что последовательность содержит хотя бы одно число (кроме нуля).
public class Solution {
public static void recursion(int sum, int count) {
java.util.Scanner in = new java.util.Scanner(System.in);
int n = in.nextInt();
// Базовый случай
if (n > 0) {
// Шаг рекурсии / рекурсивное условие
recursion(sum + n, ++count);
} else if (sum > 0 && count > 0) {
System.out.println((float) sum / count);
}
}
public static void main(String[] args) {
recursion(0, 0); // вызов рекурсивной функции
}
}
O: Второй максимум
Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите значение второго по величине элемента в этой последовательности, то есть элемента, который будет наибольшим, если из последовательности удалить наибольший элемент.
В этой задаче нельзя использовать глобальные переменные. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметра. В программе на языке Python функция возвращает результат в виде кортежа из нескольких чисел и функция вообще не получает никаких параметров. В программе на языке C++ результат записывается в переменные, которые передаются в функцию по ссылке. Других параметров, кроме как используемых для возврата значения, функция не получает.
Гарантируется, что последовательность содержит хотя бы два числа (кроме нуля).
public class Solution {
public static void recursion(int max1, int max2) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
// Базовый случай
if (n > 0) {
// Шаг рекурсии / рекурсивное условие
if (max1 < n) {
recursion(n, max1);
} // Шаг рекурсии / рекурсивное условие
else if (max2 < n) {
recursion(max1, n);
} // Шаг рекурсии / рекурсивное условие
else {
recursion(max1, max2);
}
} else {
System.out.println(max2);
}
}
public static void main(String[] args) {
recursion(0, 0); // вызов рекурсивной функции
}
}
P: Количество элементов, равных максимуму
Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите, какое количество элементов этой последовательности, равны ее наибольшему элементу.
В этой задаче нельзя использовать глобальные переменные. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметра. В программе на языке Python функция возвращает результат в виде кортежа из нескольких чисел и функция вообще не получает никаких параметров. В программе на языке C++ результат записывается в переменные, которые передаются в функцию по ссылке. Других параметров, кроме как используемых для возврата значения, функция не получает.
Гарантируется, что последовательность содержит хотя бы одно число (кроме нуля).
public class Solution {
public static void recursion(int max, int count) {
java.util.Scanner in = new java.util.Scanner(System.in);
int n = in.nextInt();
// Базовый случай
if (n > 0) {
// Шаг рекурсии / рекурсивное условие
if (n > max) {
recursion(n, 1);
} // Шаг рекурсии / рекурсивное условие
else if (n == max) {
recursion(max, ++count);
} // Шаг рекурсии / рекурсивное условие
else {
recursion(max, count);
}
} else {
System.out.println(count);
}
}
public static void main(String[] args) {
recursion(0, 0); // вызов рекурсивной функции
}
}
Q: Количество единиц
Дана последовательность натуральных чисел (одно число в строке), завершающаяся двумя числами 0 подряд. Определите, сколько раз в этой последовательности встречается число 1. Числа, идущие после двух нулей, необходимо игнорировать.
В этой задаче нельзя использовать глобальные переменные и параметры, передаваемые в функцию. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметров.
public class Solution {
public static int recursion() {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
// Базовый случай
if (n == 1) {
int m = in.nextInt();
// Базовый случай
if (m == 1) {
// Шаг рекурсии / рекурсивное условие
return recursion() + n + m;
} else {
int k = in.nextInt();
// Базовый случай
if (k == 1) {
// Шаг рекурсии / рекурсивное условие
return recursion() + n + m + k;
} else {
return n + m + k;
}
}
} else {
int m = in.nextInt();
// Базовый случай
if (m == 1) {
// Шаг рекурсии / рекурсивное условие
return recursion() + n + m;
} else {
return n + m;
}
}
}
public static void main(String[] args) {
System.out.println(recursion()); // вызов рекурсивной функции
}
}
R: Треугольная последовательность
Дана монотонная последовательность, в которой каждое натуральное число k встречается ровно k раз: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4,…
По данному натуральному n выведите первые n членов этой последовательности. Попробуйте обойтись только одним циклом for.
public class Solution {
public static String recursion(int n) {
int sum = 0;
int j = 0;
// Базовый случай
if (n == 1) {
System.out.print("1");
} else {
for (int i = 1; sum < n; i++) {
sum += i;
j = i;
}
// Шаг рекурсии / рекурсивное условие
System.out.print(recursion(--n) + " " + j);
}
return "";
}
public static void main(String[] args) {
recursion(5); // вызов рекурсивной функции
}
}
S: Заданная сумма цифр
Даны натуральные числа k и s. Определите, сколько существует k-значных натуральных чисел, сумма цифр которых равна d. Запись натурального числа не может начинаться с цифры 0.
В этой задаче можно использовать цикл для перебора всех цифр, стоящих на какой-либо позиции.
public class Solution {
public static int recursion(int len, int sum, int k, int s) {
// Базовый случай
if (len == k) {
if (sum == s) {
return 1;
} else {
return 0;
}
}
int c = (len == 0 ? 1 : 0);
int res = 0;
// Шаг рекурсии / рекурсивное условие
for (int i = c; i < 10; i++) {
res += recursion(len + 1, sum + i, k, s);
}
return res;
}
public static void main(String[] args) {
System.out.println(recursion(0, 0, 3, 15)); // вызов рекурсивной функции
}
}
T: Без двух нулей
Даны числа a и b. Определите, сколько существует последовательностей из a нулей и b единиц, в которых никакие два нуля не стоят рядом.
public class Solution {
public static int recursion(int a, int b) {
// Базовый случай
if (a > b + 1) {
return 0;
}
// Базовый случай
if (a == 0 || b == 0) {
return 1;
}
// Шаг рекурсии / рекурсивное условие
return recursion(a, b - 1) + recursion(a - 1, b - 1);
}
public static void main(String[] args) {
System.out.println(recursion(5, 8)); // вызов рекурсивной функции
}
}
U: Разворот числа
Дано число n, десятичная запись которого не содержит нулей. Получите число, записанное теми же цифрами, но в противоположном порядке.
При решении этой задачи нельзя использовать циклы, строки, списки, массивы, разрешается только рекурсия и целочисленная арифметика.
Фунция должна возвращать целое число, являющееся результатом работы программы, выводить число по одной цифре нельзя.
Update от Eivind
public class Solution {
public static int recursion(int n, int i) {
return (n==0) ? i : recursion( n/10, i*10 + n%10 );
}
public static void main(String[] args) {
System.out.println(recursion(158, 0));
}
}
Вот и все. Надеюсь решение задач принесло вам столько же удовольствия сколько и мне!
Статья носит информативный характер и в основном расчитана для людей не имеющих большого опыта с рекурсией.
И конечно же, отмечу что, решения задач написанные мной могут не являться самыми эффективными и легкими в понимании. Было бы полезно и интересно увидеть ваши варианты в коментариях.
Буду также очень рад вашим отзывам и замечаниям.
Спасибо!
P.S.: И на последок шутки про рекурсию и еще шутки про рекурсию
Автор: Khayyam




![Как обхитрить мозг и заставить его полюбить сложные задачи [Дофаминовый детокс] Как обхитрить мозг и заставить его полюбить сложные задачи [Дофаминовый детокс]](https://www.pvsm.ru/wp-content/plugins/contextual-related-posts/timthumb/timthumb.php?src=http%3A%2F%2Fwww.pvsm.ru%2Fimages%2F2024%2F05%2F10%2Fkak-obhitrit-mozg-i-zastavit-ego-polyubit-slojnye-zadachi-dofaminovyi-detoks-9.jpg&w=100&h=100&zc=1&q=75)
//это попроще будет задание слева направо
public class Task05 {
public static void main(String[] args) {
recursion(45621);
}
public static void recursion(int n) {
if (n > 10) {
recursion(n / 10);
}
System.out.print(n % 10 + ” “);
}
}