Несколько лет назад международная группа ученых из университетов Массачусетса, штата Пенсильвания и немецкого Мюнхена провела исследование эффективности традиционных прокси в качестве инструмента борьбы с цензурой. В результате ученые предложили новый метод обхода блокировок, основанный на теории игр. Мы подготовили адаптированный перевод основных моментов этой работы.
Введение
Подход популярных средств обхода блокировок, вроде Tor, основан на приватном и выборочном распределении IP-адресов прокси между клиентами из регионов, подвергающихся блокировкам. В результате клиенты должны оставаться незамеченными для организаций или органов, накладывающих блокировки. В случае Tor такие прокси-распределители называются бриджами.
Ключевая проблема в случае подобных сервисов – атака инсайдеров. Агенты, занимающиеся блокировками, могут сами использовать прокси, чтобы узнать их адреса и заблокировать их. Чтобы минимизировать вероятность вычисления прокси, инструменты обхода блокировок используют различные механизмы присвоения адресов.
При этом, используется подход так называемой ad hoc-эвристики, который можно обойти. Чтобы решить эту проблему ученые решили представить борьбу служб, занимающихся блокировками и сервисами по их обходу, в качестве игры. Используя теорию игр они разработали оптимальные стратегии поведения для каждой из сторон – в частности, это позволило выработать механизм распределения прокси.
Как работают традиционные системы обхода блокировок
Инструменты обхода блокировок, вроде Tor, Lantern и Psiphon используют ряд прокси вне региона с введенными ограничениями, которые используются для переключения трафика пользователей из этих регионов и его доставки к заблокированным ресурсам.
Если цензорам станет известен IP-адрес такого прокси – например, после того, как они сами им воспользуются – его легко внести в черный список и заблокировать. Поэтому в реальности IP-адреса таких прокси никогда не раскрываются, а присваивание пользователям того или иного прокси происходит с помощью различных механизмов. Например, в Tor есть система бриджей.
То есть главная задача – предоставить пользователям доступ к заблокированным ресурсам, и минимизировать вероятность раскрытия адреса прокси.
Решить эту задачу на практике не так-то просто – с высокой точностью отличать обычных пользователей от цензоров, маскирующихся от них, очень трудно. Для сокрытия информации используются эвристические механизмы. Например, Tor ограничивает число IP-адресов бриджей, доступных клиентам, тремя в рамках одного запроса.
Это не помешало властям Китая вычислить все Tor-бриджи за короткое время. Внедрение же дополнительных ограничений серьезно повлияет на юзабилити системы обхода блокировок, то есть некоторые пользователи не смогут получить доступ к прокси.
Как теория игр решает эту проблему
Описанный в работе метод построен на так называемой «игре поступления в колледж» (college admissions game). Кроме того, предполагается, что цензурирущие интернет агенты могут общаться между собой в реальном времени и использовать сложную тактику – например, не блокировать прокси сразу или же делать это моментально в зависимости от различных условий.
Как устроено поступление в колледж
Предположим, что у нас есть n студентов и m колледжей. Каждый студент составляет свой список предпочтений среди учебных заведений, основанных на каких-то критериях (то есть ранжируются только колледжи, куда поданы документы). С другой строны, колледжи тоже ранжируют студентов, направивших документы, на основе собственны предпочтений.
Прежде всего, колледж отсекает тех, кто не соответствуют критериям отбора – их не возьмут даже в случае недобора. Затем поступивших отбирают по алгоритму, который учитывает нужные параметры.
Возможно существование «нестабильных поступлений» – например, если есть два студента 1 и 2, которых приняли в колледжи a и b соответственно, но второй студент хотел бы учиться в вузе a. В случае описываемого эксперимента учитывались только стабильные связи между объектами.
Алгоритм отложенного принятия
Как уже было сказано, существует определенное число студентов, которых колледж не примет ни при каких обстоятельствах. Поэтому в алгоритме отложенного принятия делается предположение, что этим студентам не разрешается подавать документы в этот вуз. В таком случае, все студенты пытаются поступить в те колледжи, которые им нравятся больше всего.
Учебное заведение вместимостью q студентов помещает в лист ожидания q человек с наивысшим рейтингом на основе своих критериев или всех, если число поступающих меньше числа свободных мест. Остальным отказывают, и эти студенты подают документы в следующий вуз из своего списка предпочтений. Этот колледж также отбирает q студентов с наивысшим рейтингом из числа тех, кто подал документы сразу и тех, кого не взяли в первый колледж. Также снова какое-то число людей не проходит.
Процедура заканчивается, если каждый студент оказался в листе ожидания какого-то колледжа или ему было отказано во всех учебных заведениях, куда он мог поступать. В итоге колледжи финально зачисляют всех из своих листов ожидания.
При чем тут прокси
По аналогии со студентами и колледжами, ученые присваивали каждому клиенту определенный прокси. Получилась игра под названием proxy assignment game. Клиенты, включая возможных агентов-цензоров, выступают в роли студентов, которые хотят узнать адрес прокси, которые играют роль колледжей – у них есть заранее известная конечная пропускная способность.
В описанной модели есть n пользователей (клиентов) A =
{a1, a2, ..., an}, которые запрашивают доступ к прокси для обхода блокировок. Таким образом ai – это идентификатор «итого» клиента. Среди этих n пользователей, m – это агенты-цензоры, обозначаемые как J = {j1, j2, ..., jm}, остальные – обычные пользователи. Все m агентов контролируются центральным органом и получают от него инструкции.
Также считается, что есть набор прокси P = {p1, p2, ..., pl}. После каждого запроса клиент получает от объекта-дистрибутора информацию (IP-адрес) о k прокси. Время делится на интервалы-стадии, обозначаемые как t (игра начинается при t=0).
Каждый клиент использует функцию скоринга для оценки прокси. Ученые использовали функцию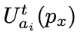 
, чтобы отметить балл, который пользователь ai присвоил прокси px на стадии t. Аналогично, каждый прокси использует функцию для оценки клиентов. То есть 
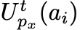– балл, который прокси px присвоил клиенту ai на стадии t.
Важно помнить, что вся игра виртуальна, то есть в нее от лица прокси и клиентов играет сам «дистрибутор». Для этого ему не нужно знать тип клиента, их предпочтения по поводу прокси. На каждой стадии происходит игра, также используется алгоритм отложенного принятия.
Результаты
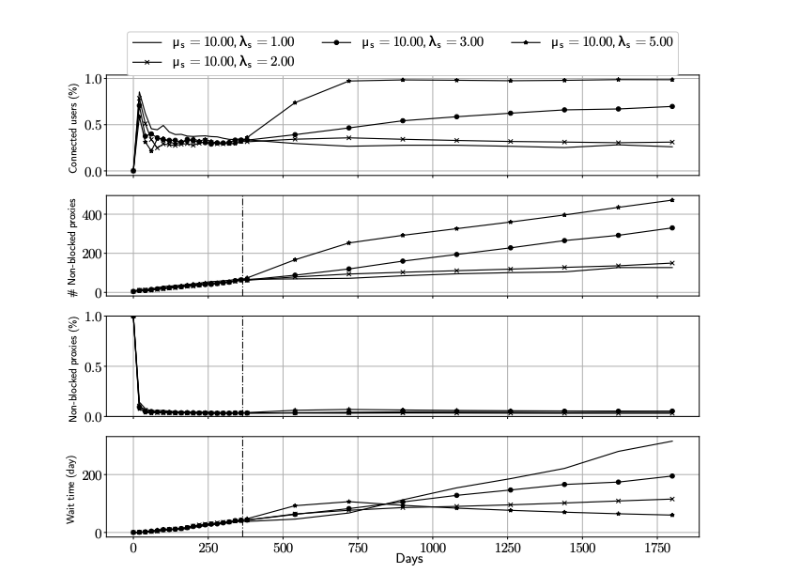
По результатам симуляций метод с использованием теории игр показал более высокую эффективность по сравнению с известными системами обхода блокировок.
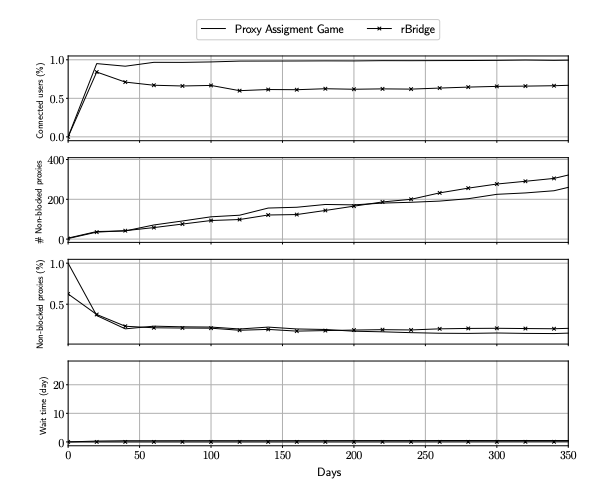
Сравнение с VPN-сервисом rBridge
При этом ученые выделили несколько важных моментов, которые могут влиять на качество работы таких систем:
- Вне зависимости от стратегии действий цензоров, система преодоления блокировок должна постоянно пополняться новыми прокси, иначе ее эффективность будет падать.
- Если у цензоров есть значительные ресурсы, они могут повысить эффективность блокировки, добавляя распределенные географически агенты для поиска прокси.
- Скорость добавления новых прокси критична для эффективности системы преодоления блокировок.
Полезные ссылки и материалы от Infatica:
- История борьбы с цензурой: как работает созданный учеными из MIT и Стенфорда метод flash proxy
- Как понять, когда прокси лгут: верификация физических локаций сетевых прокси с помощью алгоритма активной геолокации
- Как замаскироваться в интернете: сравниваем серверные и резидентные прокси
Автор: lol_wat
