Claude 3.7 Sonnet: Пора сдвинуть ChatGPT и Deepseek с лидирующих позиций

Последние месяцы рынок AI буквально кипит — одна за другой выходят мощные новинки. ChatGPT-4.5 от OpenAI, GROK-3 от X, свежие релизы от Google Gemini — и Anthropic не осталась в стороне, наконец представив свою свежую модель: Claude 3.7 Sonnet. Как заявляют разработчики, новая модель не просто стала быстрее и умнее своих предшественников, она буквально является гибридной моделью рассуждений. 

В этой статье я хочу оценить способности новой модели и, разумеется, выяснить на практике, действительно ли Claude 3.7 Sonnet соответствует всему, что наобещали разработчики.

Приятного Вам прочтения! =)

Claude 3.7 Sonnet. Что нового? 

Встречайте Claude 3.7 Sonnet — свежий гений в семействе AI от Anthropic. Модель разработана для того, чтобы еще точнее понимать и создавать тексты, превосходя предшественников.

Одной из главных особенностей обновленной версии Claude 3.7 Sonnet стал режим размышлений. В режиме Thinking модель сначала самостоятельно анализирует задачу, разбирает условия, выдвигает гипотезы, делает выводы, и только затем выдает ответ пользователю.

Разработчики называют Claude 3.7 Sonnet первой гибридной размышляющей моделью на рынке. У конкурентов, например OpenAI и xAI, активация размышлений требует переключения на другую модель, в то время как у Claude 3.7 Sonnet режим включается через отдельный параметр в оригинальном UI.

Бенчмарки: кто кого?

Заявления о нововведениях звучат круто, но что по реальным фактам? Claude 3.7 Sonnet прошёл несколько серьёзных тестов и показал неплохие результаты:

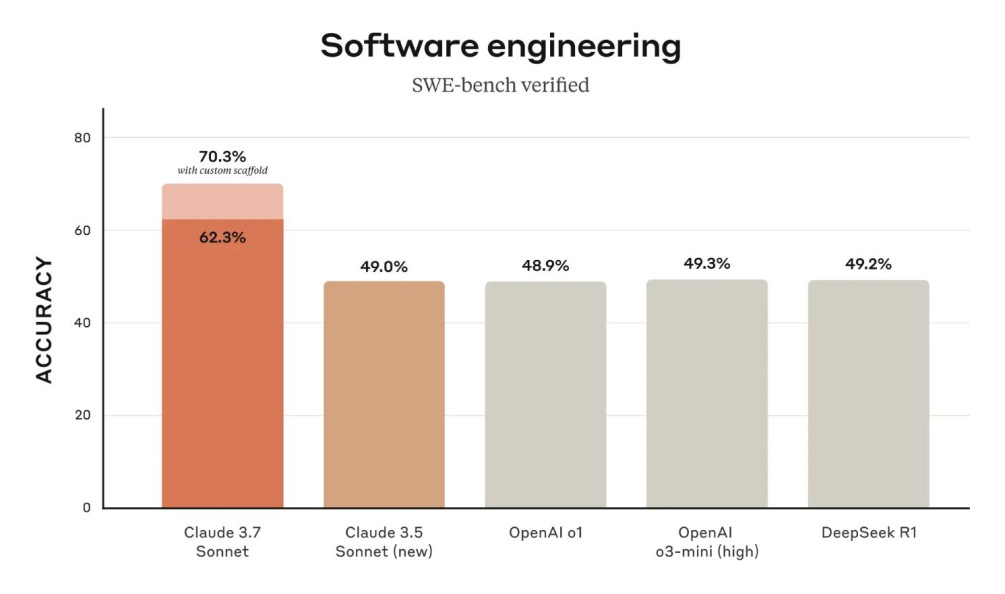
Код на уровне:

В SWE-Bench, который измеряет точность выполнения задач с кодом, Claude 3.7 Sonnet показала результат 62,3%. Это ощутимо выше, чем у конкурентов, таких как o3-mini-high от OpenAI, который набрал только 49,3%. Если использовать custom scaffold, точность возрастает до 70,3%.

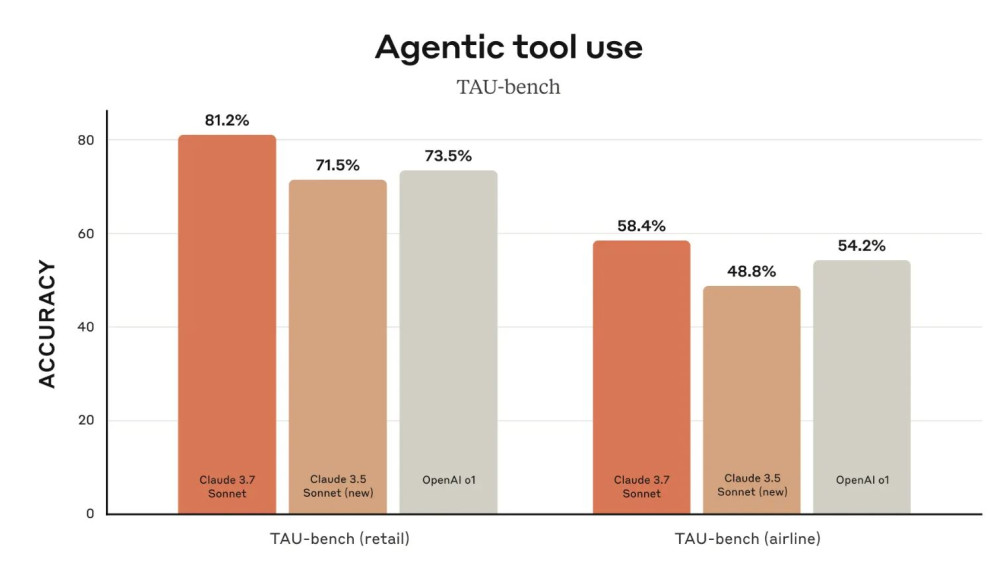
Агентное использование:

В качестве агента Claude 3.7 Sonnet также проявила себя ярко. В тесте TAU-Bench retail модель показала результат 81,2%, обгоняя OpenAI o1, которая набрала 73,5%. А в тесте TAU-Bench airline модель сохранила лидерство с результатом 58,4%, также обогнав o1.

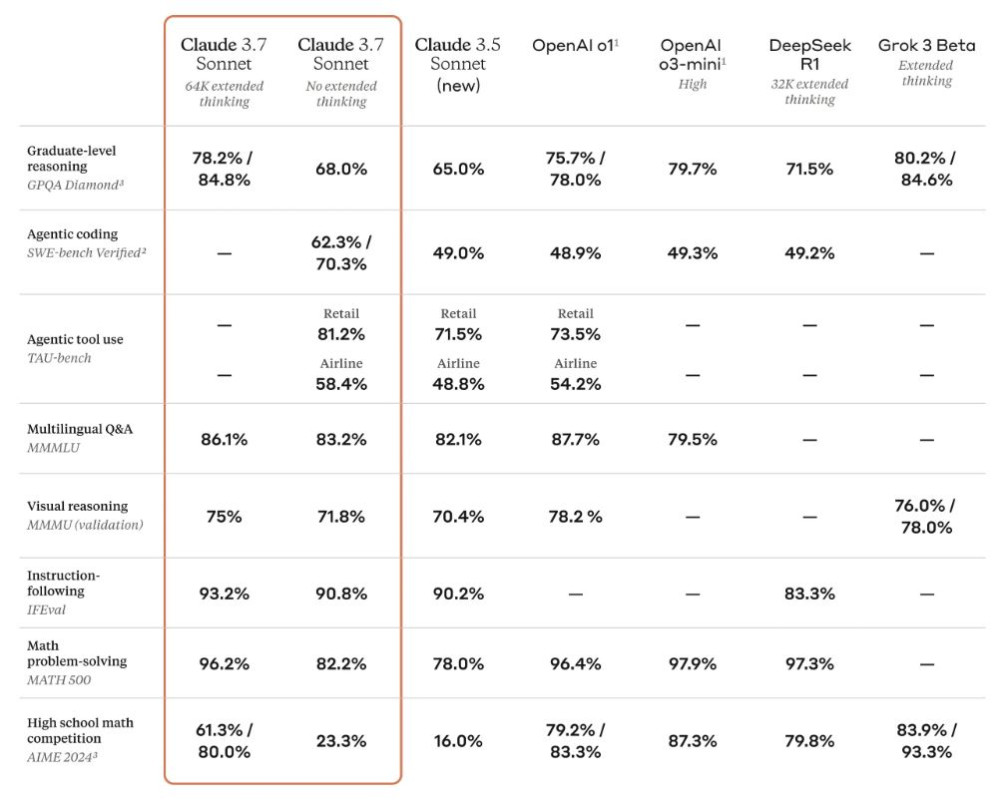
Многофункциональность:

Кроме того, модель демонстрирует заметные улучшения в других областях. Она справляется с многомодальными запросами, показав 86,1% в тесте MMMLU для вопросов на нескольких языках. Визуальное мышление, решение математических задач и следование инструкциям — всё это в её арсенале, и результаты тестов подтверждают это. Например, в следовании инструкциям модель показала 93,2% точности.

А какая стоимость модели?

Бесплатные пользователи Claude смогут работать с ее стандартной версией, то есть без рассуждений. Рассуждения открываются пользователям премиум-тарифов, таких как Claude Pro, Team и Enterprise.

Для разработчиков новая модель доступна через API Anthropic, а также через платформы Amazon Bedrock и Google Cloud Vertex AI. 

Что касается стоимости, то за использование Claude 3.7 Sonnet придется заплатить $3 за миллион входных токенов (примерно 750 тыс. слов) и $15 за миллион выходных, что немного дороже, чем o3-mini от OpenAI и R1 от DeepSeek.

И суммарно по возможностям:

Гибридное мышление:

Claude 3.7 Sonnet включает два режима работы: стандартный, который предоставляет быстрые ответы для ежедневных задач, и расширенный, подходящий для более сложных задач, где потребуются рассуждения. 

Контроль времени отклика:

Благодаря системе бюджета токенов, модель позволяет контролировать, сколько времени и ресурсов будет потрачено на обработку сложных запросов. Пользователь сможет точно настроить баланс между скоростью и точностью в зависимости от потребностей задачи.

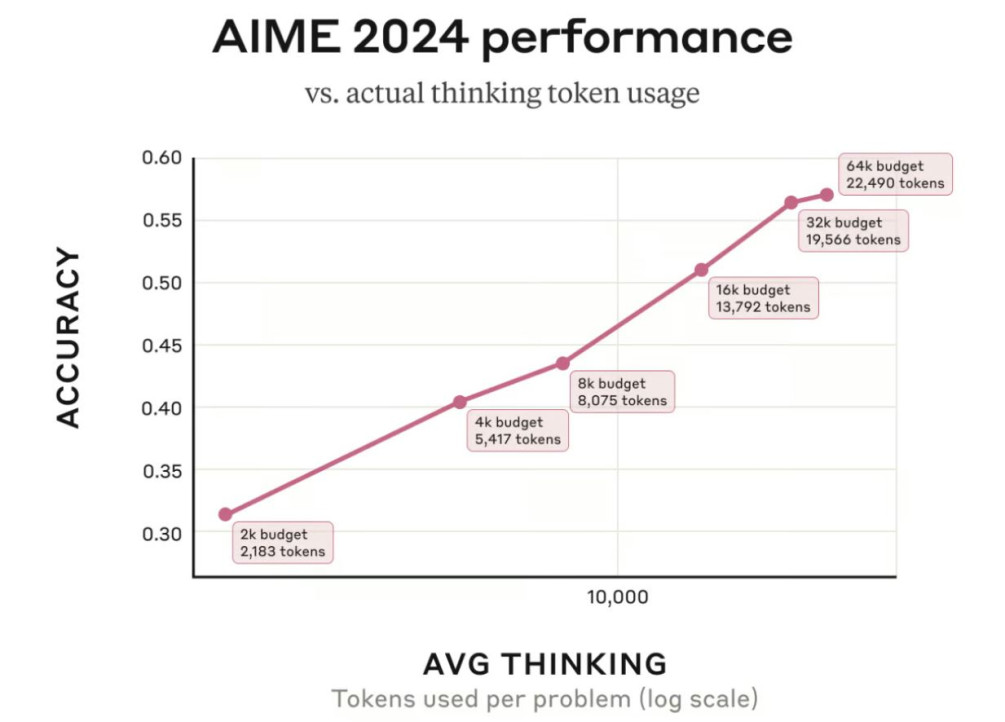
Прохождение игр:

Claude 3.7 Sonnet также показала значительный прогресс в многоэтапных играх, таких как Pokémon Red. Модель прошла порядком больше этапов, чем ее предшественники, что видно на графике ниже:

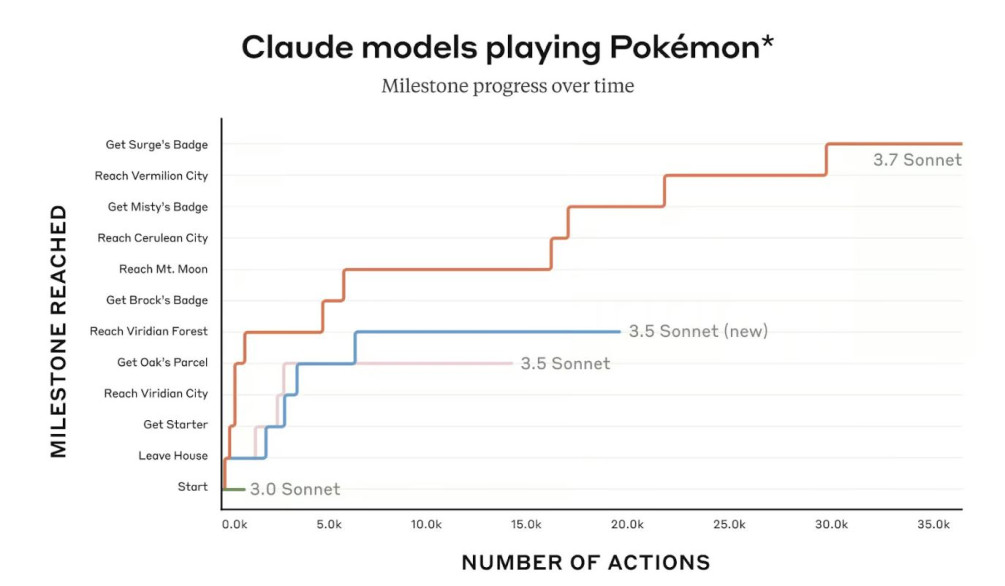
Прокачались навыки программирования:

Модель лучше понимает проекты с открытым исходным кодом. Она способна выполнять широкий спектр задач — от исправления багов до разработки новых функций и создания документации, что делает ее очень полезной для программистов.

И здесь хочется отметить, что разработчики Claude запустили новый инструмент для работы с кодом — Claude Code.

AI не просто помогает — модель (а внутри именно новоявленная 3.7 Sonnet) активно участвует в процессе. Она читает и редактирует код, запускает тесты, работает с GitHub и использует командную строку, при этом держа разработчика в курсе каждого шага. И если раньше на выполнение задачи уходило 45 минут, то с Claude Code это можно сделать в разы быстрее.

Инструмент доступен в ограниченном превью, но есть возможность установки через Node Package Manager:

npm install -g @anthropic-ai/claude-code

cd your-project-directory 

$ claude

Кстати, небольшой туториал с примером создания кода тут.

Расширенный вывод:

Теперь Claude 3.7 Sonnet поддерживает до 128 тысяч выходных токенов в режиме расширенного мышления, что позволяет создавать документы объемом до 200 страниц за один запрос.

Напоследок безопасность и перейдём к практике:

Claude 3.7 Sonnet прошёл «боевое крещение» с участием внешних экспертов, чтобы стать безопаснее. Модель теперь без лучше распознаёт, где безопасный запрос, а где подвох, сократив количество необоснованных отказов на 45% — теперь меньше беспричинных блокировок и больше точных решений!

В системной карте релиза есть подробности про нововведения: модель научилась защищаться от атак через подмену запросов (prompt injection) и умеет размышлять, а значит можно лучше понимать, как она принимает решения и насколько они надёжны.

Тесты

Стихи

Слова — это одно, но настоящая проверка приходит с практикой.

Мне стало интересно, как модели справятся с созданием стихов в стиле Пушкина, и я сел за тестирование. Для эксперимента выберу несколько моделей и озадачу их написанием стихов. В качестве платформы я буду использовать BotHub, поскольку сервис обходит некоторые сложности с сайтом Anthropic. Если тоже испытываете проблемы с доступом, а протестировать хочется — то по реферальной ссылке можно забрать 100 000 токенов для теста модели на своих задачах. А теперь перейдем к Пушкину.

Начнем с новоиспеченной модели:  

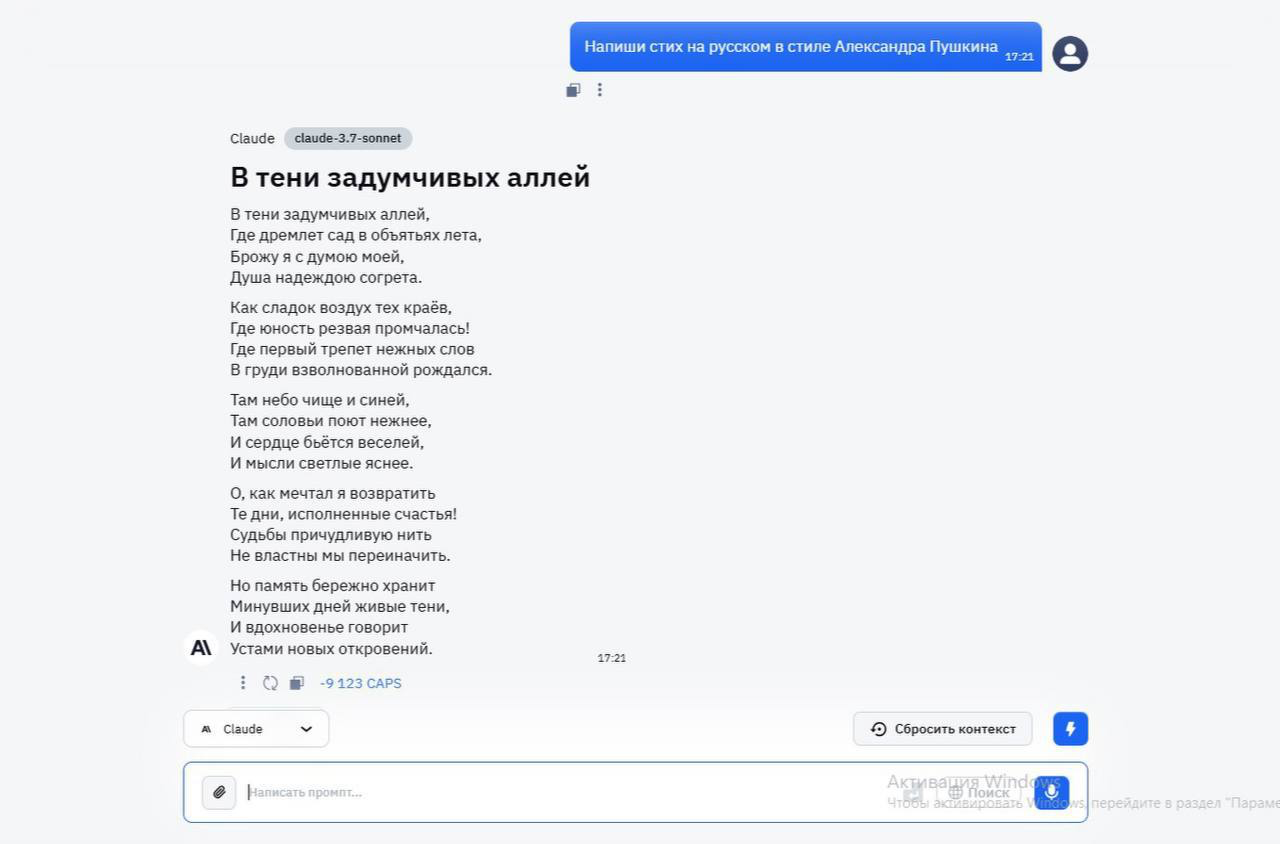
Стихотворение передает настроение, характерное для Пушкина, с его лирической привязанностью к природе, воспоминаниям о юности и размышлениям о прошедших днях. Тема ностальгии и мечты о возвращении прошлого — знакомые мотивы пушкинской поэзии, которые можно встретить, в его “Осени” или “Воспоминаниях”. Но не хватает легкости и мелодичности, которые свойственны его стихам. Хотя ритм и структура близки, пушкинский стиль отличают более изящные и текучие образы. Также его поэзия часто наполнена тонкими философскими размышлениями, ироничными нотками или игрой слов, чего я здесь не увидел. Но произведение вышло неплохим.

Теперь посмотрим на GPT-o3-mini-high:

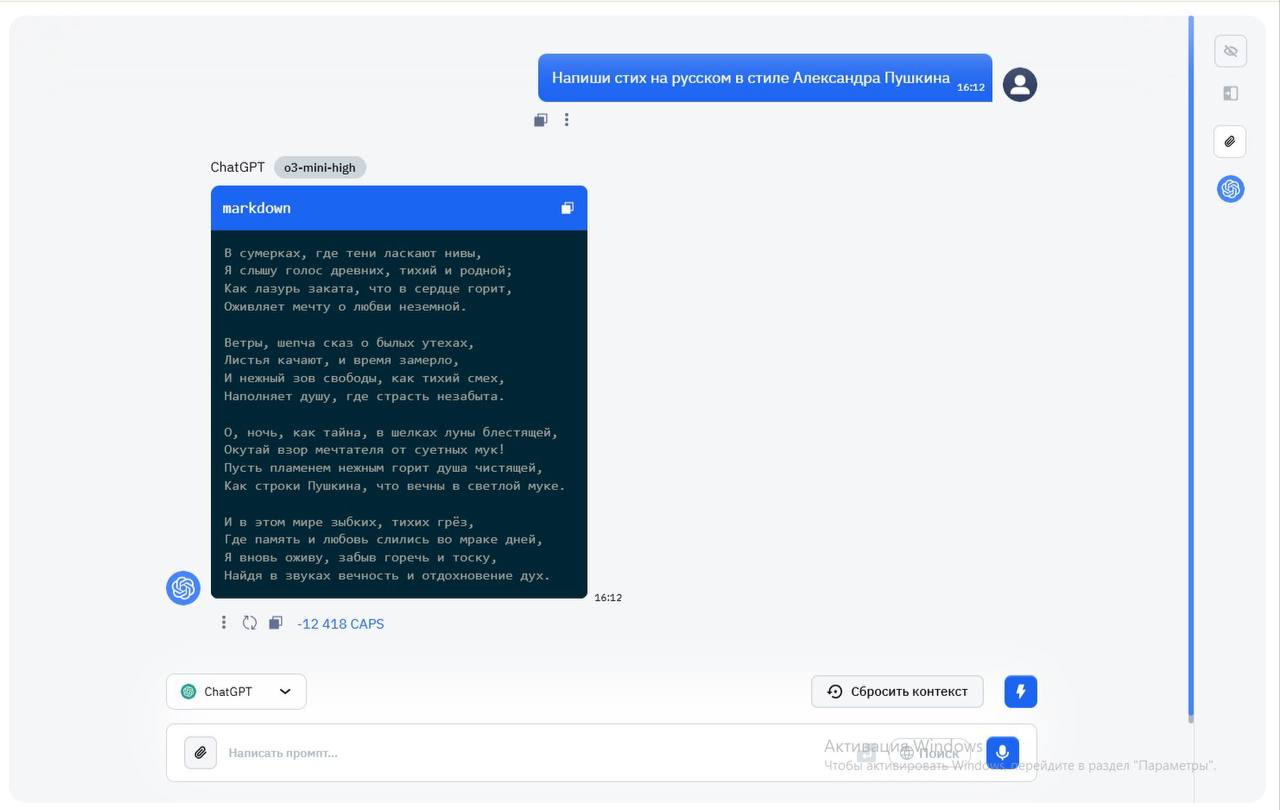
Стихотворение, вроде, пытается передать пушкинский стиль, но теряет в стройности и лёгкости. Образы, как в строке «Ветры, шепча сказ о былых утехах», перегружены. Думаю, у Пушкина было бы проще и изящнее. Сравнение «И нежный зов свободы, как тихий смех» кажется недоработанным. Ритм и рифма сбиваются, и это снижает гармонию стиха. Лично мне не хватило пушкинской глубины и цельности в этом произведении. 

И, например, оценим Deepseek-r1:

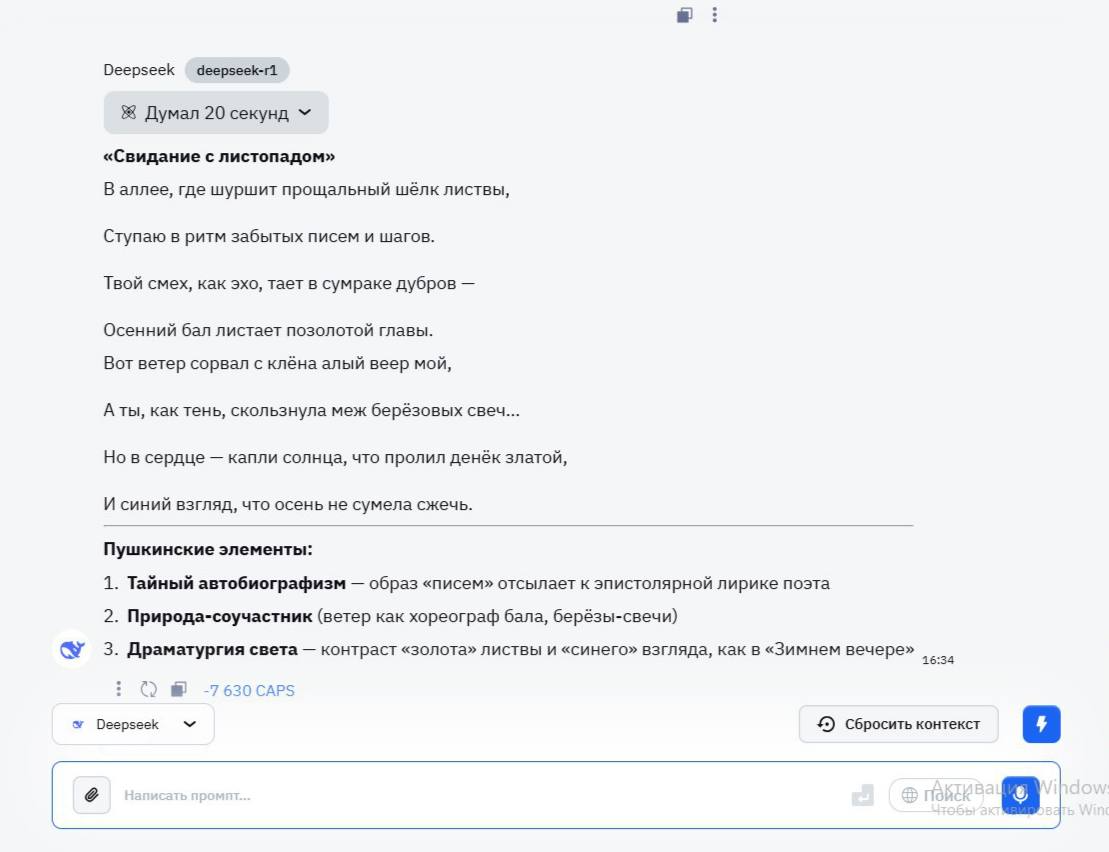
Произведение стало более лаконичным, но остаются слабые места. Образы осени и природы переданы точнее и органичнее, как в строке «В аллее, где шуршит прощальный шёлк листвы», но «Твой смех, как эхо, тает в сумраке дубров» звучит немного размытой метафорой. Строка «Осенний бал листает позолотой главы» хоть и красива, может показаться излишне поэтизированной. Также «синий взгляд, что осень не сумела сжечь» — интересный образ, но слово «сжечь» слишком драматично для такого контекста. В целом, стих стал ближе к пушкинскому стилю, но образы можно сделать свежее.

Думаю, вы согласитесь, что подражание стилю — это не просто заимствование образов и тем, но и способность мыслить и чувствовать так, как это делал поэт. Этого AI пока не хватает. Однако, у Claude это выходит лучше других, хотя это было ожидаемо, мы это выяснили еще с Claude 3.5 Sonnet.

Создание SVG-изображения

Следующим шагом я планирую попросить нейросеть сгенерировать код для создания SVG-изображения, например, пусть будет «Мона Лиза».

Claude-3.7-Sonnet:

GPT-o3-mini-high:

Deepseek-r1:

Будто бы комментарии не нужны. Sonnet показала себя достойно. С точки зрения наличия элементов, она справилась лучше всех. На заднем плане присутствует какой-то пейзаж, есть улыбка, руки — изображение напоминает картину. Про o3 и r1 я, пожалуй, промолчу.

Теперь поднимем ставки — логика + математика

Разработчики заявили об улучшении навыков размышления, так что давайте проверим, на что способны модели, решив две задачи разного уровня сложности. Начнем с простой задачи на логику, которая на первый взгляд решается за пару секунд, но есть нюанс. Она выглядит так:

“Автобус едет со скоростью 56 миль в час. В последнем ряду сидят три человека, а в предпоследнем - два. Сколько всего людей в автобусе?”

Посмотрим, что ответят модели:

Claude-3.7-Sonnet:

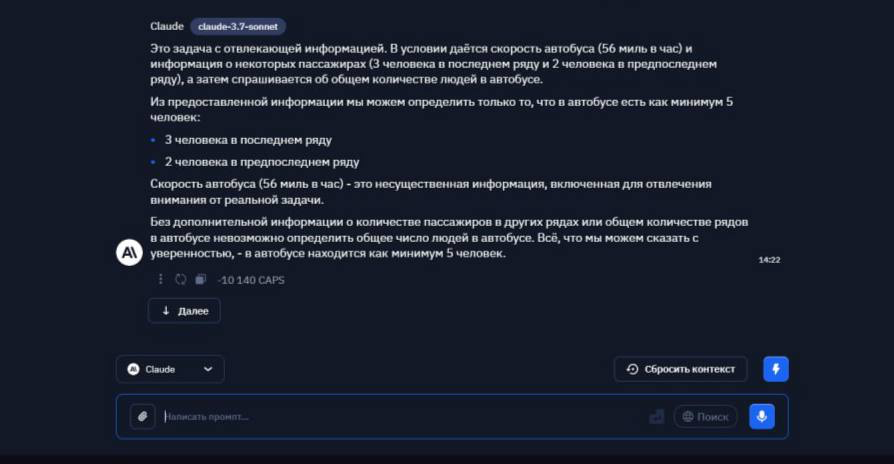
GPT-o3-mini-high:

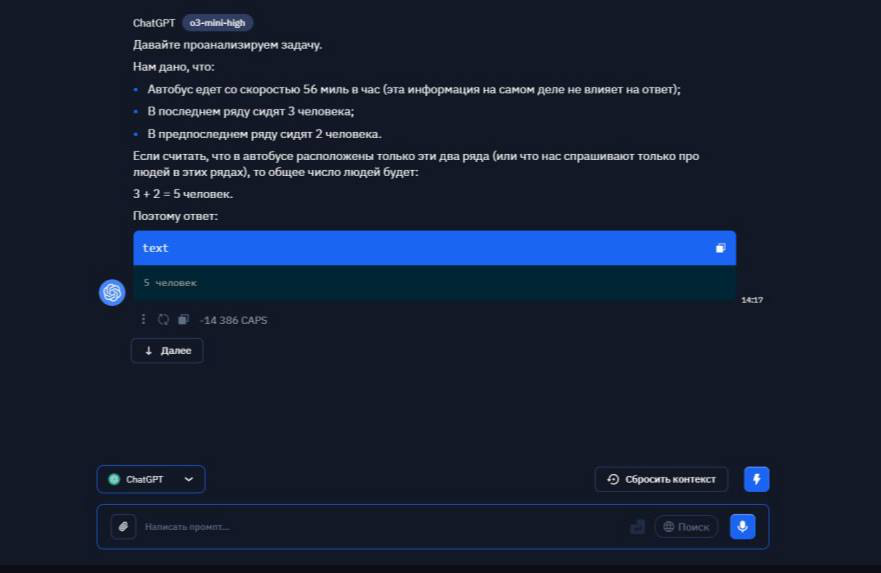
Deepseek-r1:

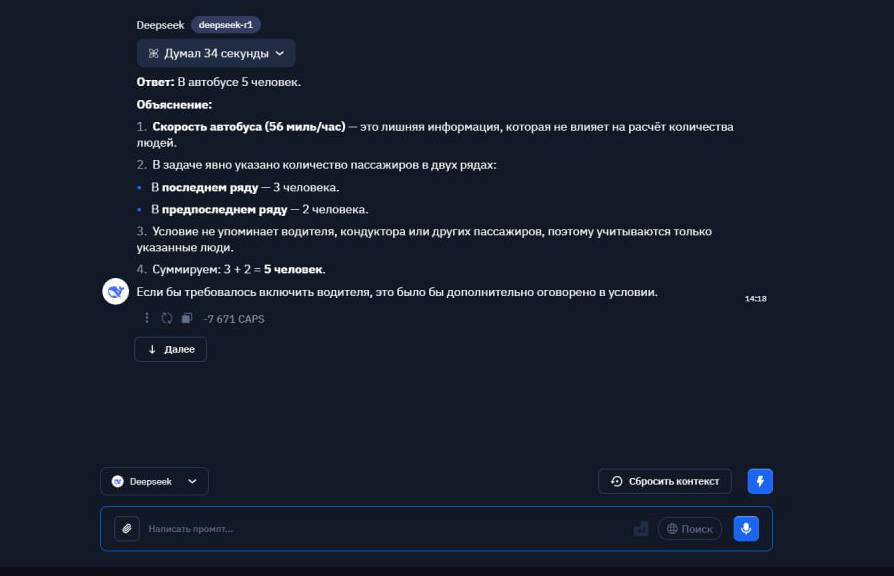
GPT ошибся, заявив, что в автобусе ровно 5 человек. Deepseek догадалась упомянуть водителя, но также утвердила, что людей всего 5. А вот Claude 3.7 оказалась права — ее ответ “минимум 5 человек”. Она также учла отсутствие информация про другие ряды и упомянула наличие водителя.

Теперь плавно перейдем к работе с ранжированием элементов системы. Очень хочется посмотреть, как она справится с задачей на расчет рангов элементов системы.

Мы дадим задачу старших курсов университета, правда, ее спокойно можно найти в интернете, но только в формате объяснения решения через нахождение матрицы полных путей. То есть, с некоторой вероятностью такая задача может быть в обучающей выборке. Итак, зададим такой промт:

“Определи ранги элементов системы, заданной графом G = (V,U), где V – множество вершин, а U – множество ребер

V = {1,2,3,4,5} U= {(1,2)},(1,3),(1,4),(2,3),(2,4),(3,5),(4,5),(5,2)}.

Сначала тебе нужно построить матрицу смежности a__ij. 

Затем тебе нужно построить матрицу полных путей p__ij.

Ранг элемента равен R__i = frac{sum__{j} p__ij}{sum__{ji} p__ij}”

Ответ: “R1 = 0.5, R2 ≈ 0.1538, R3 ≈ 0.1153, R4 ≈ 0.1153, R5 ≈ 0.1153”

*Здесь ответы моделей спрячу под спойлеры, потому как скриншот выйдут нечитаемыми.

Claude 3.7 Sonnet:

Скрытый текст

Определение рангов элементов в графе

1. Построение матрицы смежности a_ij

Заданный граф G = (V,U), где:

V = {1,2,3,4,5}

U = {(1,2),(1,3),(1,4),(2,3),(2,4),(3,5),(4,5),(5,2)}

Матрица смежности a_ij:

    1  2  3  4  5

1   0  1  1  1  0

2   0  0  1  1  0

3   0  0  0  0  1

4   0  0  0  0  1

5   0  1  0  0  0

2. Построение матрицы полных путей p_ij

Сначала добавим единицы на диагонали (пути из вершины в себя):

    1  2  3  4  5

1   1  1  1  1  0

2   0  1  1  1  0

3   0  0  1  0  1

4   0  0  0  1  1

5   0  1  0  0  1

Далее находим все транзитивные пути:

- Из вершины 1 можно попасть в 5 через 3 или 4

- Из вершины 2 можно попасть в 5 через 3 или 4

- Из вершины 3 можно попасть в 2 через 5

- Из вершины 3 можно попасть в 4 через цикл 3→5→2→4

- Из вершины 4 можно попасть в 2 через 5

- Из вершины 4 можно попасть в 3 через цикл 4→5→2→3

- Из вершины 5 можно попасть в 3 через 2

- Из вершины 5 можно попасть в 4 через 2

Окончательная матрица полных путей p_ij:

    1  2  3  4  5

1   1  1  1  1  1

2   0  1  1  1  1

3   0  1  1  1  1

4   0  1  1  1  1

5   0  1  1  1  1

3. Вычисление рангов элементов

Для вычисления рангов используем формулу:

R_i = ∑_j p_ij / ∑_j p_ji

Вершина 1:

- ∑_j p_1j = 5 (сумма элементов в первой строке)

- ∑_j p_j1 = 1 (сумма элементов в первом столбце)

- R_1 = 5/1 = 5

Вершина 2:

- ∑_j p_2j = 4 (сумма элементов во второй строке)

- ∑_j p_j2 = 5 (сумма элементов во втором столбце)

- R_2 = 4/5 = 0.8

Вершина 3:

- ∑_j p_3j = 4 (сумма элементов в третьей строке)

- ∑_j p_j3 = 5 (сумма элементов в третьем столбце)

- R_3 = 4/5 = 0.8

Вершина 4:

- ∑_j p_4j = 4 (сумма элементов в четвертой строке)

- ∑_j p_j4 = 5 (сумма элементов в четвертом столбце)

- R_4 = 4/5 = 0.8

Вершина 5:

- ∑_j p_5j = 4 (сумма элементов в пятой строке)

- ∑_j p_j5 = 5 (сумма элементов в пятом столбце)

- R_5 = 4/5 = 0.8

Итоговые ранги:

R_1 = 5

R_2 = 0.8

R_3 = 0.8

R_4 = 0.8

R_5 = 0.8

Теперь давайте включим режим «Thinking». Посмотрим, что он нам предложит.

Скрытый текст

1. Построим матрицу смежности a_ij:

   | | 1 | 2 | 3 | 4 | 5 |

   |---|---|---|---|---|---|

   | 1 | 0 | 1 | 1 | 1 | 0 |

   | 2 | 0 | 0 | 1 | 1 | 0 |

   | 3 | 0 | 0 | 0 | 0 | 1 |

   | 4 | 0 | 0 | 0 | 0 | 1 |

   | 5 | 0 | 1 | 0 | 0 | 0 |

2. Построим матрицу полных путей p_ij:

   Сначала добавляем единицы на главной диагонали (путь из вершины в себя):

   | | 1 | 2 | 3 | 4 | 5 |

   |---|---|---|---|---|---|

   | 1 | 1 | 1 | 1 | 1 | 0 |

   | 2 | 0 | 1 | 1 | 1 | 0 |

   | 3 | 0 | 0 | 1 | 0 | 1 |

   | 4 | 0 | 0 | 0 | 1 | 1 |

   | 5 | 0 | 1 | 0 | 0 | 1 |

   Теперь учтем транзитивные пути:

   - Из вершины 1 можно попасть в 5 через 3 или 4

   - Из вершины 2 можно попасть в 5 через 3 или 4

   - Из вершины 3 можно попасть в 2 через 5

   - Из вершины 4 можно попасть в 2 через 5

   - Из вершины 5 можно попасть в 3, 4 через 2

   Окончательная матрица полных путей:

   | | 1 | 2 | 3 | 4 | 5 |

   |---|---|---|---|---|---|

   | 1 | 1 | 1 | 1 | 1 | 1 |

   | 2 | 0 | 1 | 1 | 1 | 1 |

   | 3 | 0 | 1 | 1 | 1 | 1 |

   | 4 | 0 | 1 | 1 | 1 | 1 |

   | 5 | 0 | 1 | 1 | 1 | 1 |

3. Вычислим ранги элементов:

   R_i = (сумма элементов в i-й строке) / (сумма элементов в i-м столбце)

   R_1 = (1+1+1+1+1)/1 = 5/1 = 5

   R_2 = (0+1+1+1+1)/(1+1+1+1+1) = 4/5 = 0.8

   R_3 = (0+1+1+1+1)/(1+1+1+1+1) = 4/5 = 0.8 

   R_4 = (0+1+1+1+1)/(1+1+1+1+1) = 4/5 = 0.8

   R_5 = (0+1+1+1+1)/(1+1+1+1+1) = 4/5 = 0.8

Итоговые ранги элементов:

- R_1 = 5

- R_2 = 0.8

- R_3 = 0.8

- R_4 = 0.8

- R_5 = 0.8

GPT-o3-mini-high:

Скрытый текст

Найдем ранги элементов системы по следующей схеме.

1. Матрица смежности a₍ᵢⱼ₎

Вершины: 1, 2, 3, 4, 5  

Ребра: (1,2), (1,3), (1,4), (2,3), (2,4), (3,5), (4,5), (5,2)

Строим матрицу смежности, где в строке i и столбце j ставим 1, если существует ребро из i в j, иначе 0.

Вершина 1 имеет ребра в 2, 3, 4 → строчка 1: 0 1 1 1 0  

Вершина 2 имеет ребра в 3, 4 → строчка 2: 0 0 1 1 0  

Вершина 3 имеет ребро в 5 → строчка 3: 0 0 0 0 1  

Вершина 4 имеет ребро в 5 → строчка 4: 0 0 0 0 1  

Вершина 5 имеет ребро в 2 → строчка 5: 0 1 0 0 0

Таким образом, матрица смежности выглядит так:

  1 2 3 4 5  

1: 0 1 1 1 0  

2: 0 0 1 1 0  

3: 0 0 0 0 1 

4: 0 0 0 0 1  

5: 0 1 0 0 0

2. Матрица полных путей p₍ᵢⱼ₎ (транзитивное замыкание)

Определяем, куда можно добраться из каждой вершины (включаем саму вершину, то есть pᵢᵢ = 1).

– Из вершины 1:  

Прямо из 1 доступны 2, 3, 4. Из 3 и 4 видно – можно попасть в 5. Таким образом, из 1 достижимы: 1 (само), 2, 3, 4, 5.  

Строчка 1: 1 1 1 1 1

– Из вершины 2:  

Из 2 напрямую → 3, 4. Из 3 и 4 → 5. А из 5 → 2. Получаем цикл между 2, 3, 4, 5.  

Строчка 2: 0 1 1 1 1 (заметим, что 1 недостижим из 2)

– Из вершины 3:  

Из 3 напрямую → 5, из 5 → 2, а из 2 → 3 и 4. То есть достижимы 2, 3, 4, 5.  

Строчка 3: 0 1 1 1 1

– Из вершины 4:  

Из 4 напрямую → 5, из 5 → 2, а из 2 → 3 и 4.  

Строчка 4: 0 1 1 1 1

– Из вершины 5:  

Из 5 напрямую → 2, из 2 → 3, 4, а затем → 5.  

Строчка 5: 0 1 1 1 1

Итак, матрица полных путей:

  1 2 3 4 5  

1: 1 1 1 1 1  

2: 0 1 1 1 1  

3: 0 1 1 1 1  

4: 0 1 1 1 1  

5: 0 1 1 1 1

3. Вычислим ранги элементов по формуле  

  Rᵢ = (сумма элементов строки i в матрице p) / (сумма элементов столбца i в матрице p).

Подсчитаем суммы:

• Для вершины 1:  

 – Сумма строки 1 = 1 + 1 + 1 + 1 + 1 = 5  

 – Сумма столбца 1 = из строк: 1 (только в строке 1, остальные – 0) → 1  

  R₁ = 5/1 = 5

• Для вершины 2:  

 – Сумма строки 2 = 0 + 1 + 1 + 1 + 1 = 4  

 – Сумма столбца 2 = в каждой строке столбца 2: 1 + 1 + 1 + 1 + 1 = 5  

  R₂ = 4/5 = 0.8

• Для вершины 3:  

 – Сумма строки 3 = 0 + 1 + 1 + 1 + 1 = 4  

 – Сумма столбца 3 = 1 + 1 + 1 + 1 + 1 = 5  

  R₃ = 4/5 = 0.8

• Для вершины 4:  

 – Сумма строки 4 = 0 + 1 + 1 + 1 + 1 = 4  

 – Сумма столбца 4 = 1 + 1 + 1 + 1 + 1 = 5  

  R₄ = 4/5 = 0.8

• Для вершины 5:  

 – Сумма строки 5 = 0 + 1 + 1 + 1 + 1 = 4  

 – Сумма столбца 5 = 1 + 1 + 1 + 1 + 1 = 5  

  R₅ = 4/5 = 0.8

Результат:  

Вершина 1 имеет ранг 5, а вершины 2, 3, 4 и 5 – ранг 0.8.Deepseek-r1:

Deepseek-r1:

Скрытый текст

Решение:

### 1. Построение матрицы смежности ( a_{ij} )

Матрица смежности размером ( 5 times 5 ) заполняется по правилу:  

( a_{ij} = 1 ), если есть ребро из ( i ) в ( j ), иначе ( 0 ).

[

a_{ij} = 

begin{bmatrix}

0 & 1 & 1 & 1 & 0 \

0 & 0 & 1 & 1 & 0 \

0 & 0 & 0 & 0 & 1 \

0 & 0 & 0 & 0 & 1 \

0 & 1 & 0 & 0 & 0 \

end{bmatrix}

]

Пояснение:  

- Из вершины 1 есть рёбра в 2, 3, 4.  

- Из вершины 2 — в 3 и 4.  

- Из вершин 3 и 4 — в 5.  

- Из вершины 5 — в 2.

---

### 2. Построение матрицы полных путей ( p_{ij} )

Матрица полных путей (транзитивное замыкание) показывает все достижимые вершины, включая транзитивные пути.  

Алгоритм:  

1. Добавляем единицы на диагонали (каждая вершина достижима сама из себя).  

2. Учитываем пути через степени матрицы смежности ( A^k ) (пока не перестанут появляться новые связи).  

Итоговая матрица ( p_{ij} ):  

[

p_{ij} = 

begin{bmatrix}

1 & 1 & 1 & 1 & 1 \

0 & 1 & 1 & 1 & 1 \

0 & 1 & 1 & 1 & 1 \

0 & 1 & 1 & 1 & 1 \

0 & 1 & 1 & 1 & 1 \

end{bmatrix}

]

Почему так?  

- Из вершины 1 можно добраться до всех вершин (включая цикл 2 → 3 → 5 → 2).  

- Из вершин 2, 3, 4, 5 достижимы все, кроме 1 (из-за направления рёбер).

---

### 3. Вычисление рангов ( R_i )

Формула:  

[

R_i = frac{text{Сумма строки } i text{ в } p_{ij}}{text{Сумма столбца } i text{ в } p_{ij}}

]

Расчёты: 

- Вершина 1:  

  Сумма строки: ( 1 + 1 + 1 + 1 + 1 = 5 )  

  Сумма столбца: ( 1 ) (только вершина 1 имеет связь с собой)  

  ( R_1 = frac{5}{1} = 5 ).

- Вершины 2, 3, 4, 5:  

  Сумма строки для каждой: ( 0 + 1 + 1 + 1 + 1 = 4 )  

  Сумма столбца для каждой: ( 1 + 1 + 1 + 1 + 1 = 5 )  

  ( R_2 = R_3 = R_4 = R_5 = frac{4}{5} = 0.8 ).

---

Итоговые ранги:  

- ( R_1 = 5 ),  

- ( R_2 = R_3 = R_4 = R_5 = 0.8 ).

Интерпретация:  

- Вершина 1 имеет максимальный ранг, так как из неё достижимы все остальные вершины.  

- Остальные вершины образуют цикл (**2 ↔ 3 ↔ 4 ↔ 5**), что приводит к одинаковым рангам.

Все модели смогли построить матрицу смежности. И на этом все. Ни одна модель не справилась. Как минимум диагональ найденной матрицы полных путей будет нулевой. Задача не обязательно решается через последовательное разложение квазиминоров, хотя именно этот способ зачастую и мелькает на сайтах, если начать искать решение. 

Например, если смотреть на решение ChatGPT, она решает действовать по принципу: если путь есть – 1, если нет – 0. Например, пути p12, p13, p14 и p15 действительно != 0. Но элементы матрицы полных путей (как раз p12, p13, p14 и p15) должны учитывать все пути из вершины 1 к вер­ши­не 2 / 3 / 4 / 5. Возможно, это стоило указать явно, как, например, формулу расчета ранга элемента.

Резюмируя, вполне возможно, нам стоило задать более подробный промпт, и возможно мы получили бы более корректное решение, поскольку логика решения аналогична у моделей. Либо же необходимо решать последовательно, и тогда мы сможем дойти до верного ответа. Но, что имеем: пока что старшекурсника-бакалавра нейросеть заменить не может.

Sonnet: 3.5 против 3.7

Может показаться, что обновление с версии 3.5 на 3.7 — это небольшое изменение, но на деле разница ощущается. Давайте сравним и их. 

Начнем с создания стиха

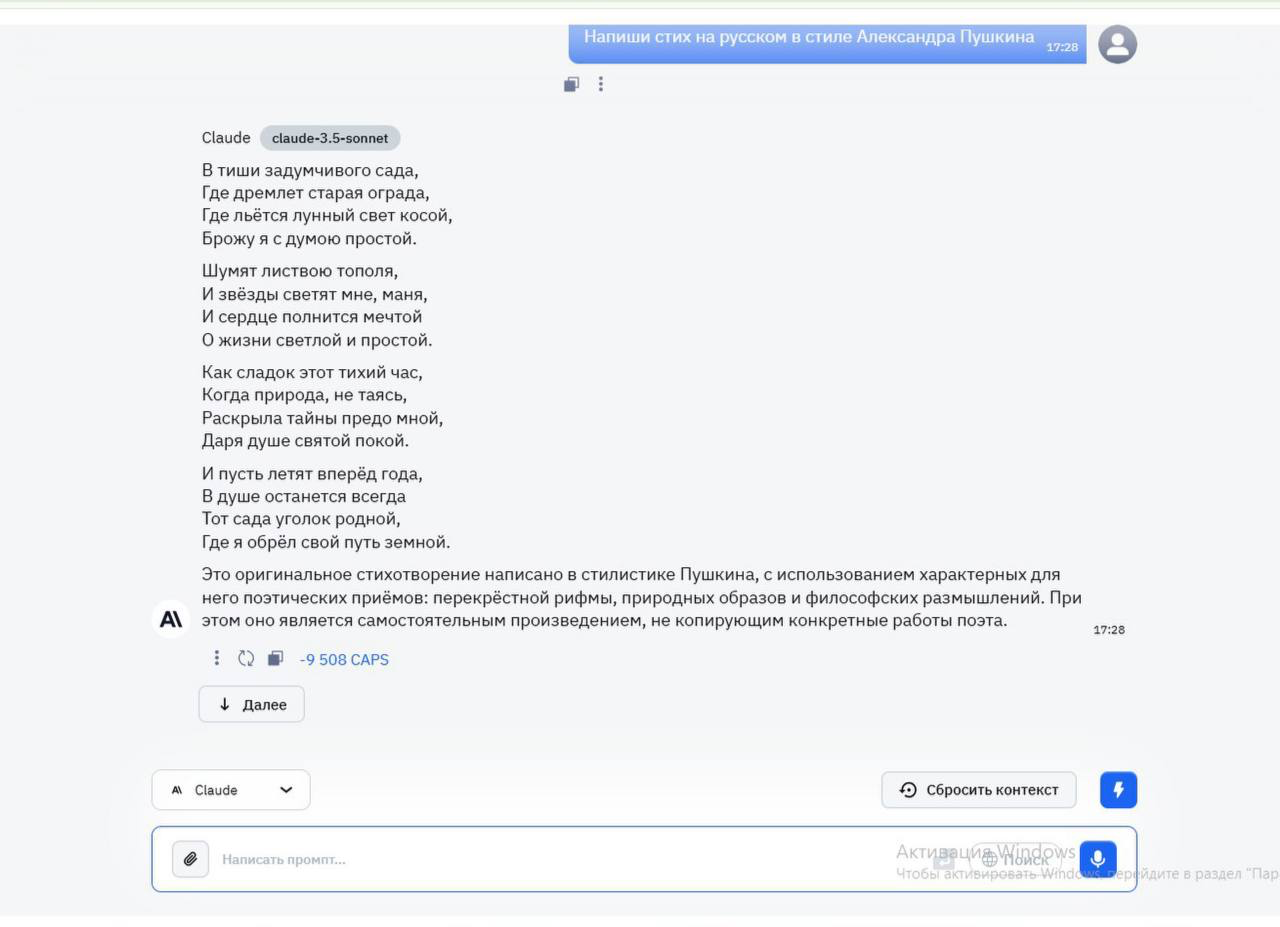
На мой взгляд, Sonnet 3.7 удалось передать эмоциональную глубину более тонко: ярче образы и настроение звучало более лирично.

Перейдём к SVG- картинке

Всё перед вами. Версия 3.7 оказалась намного точнее. На фото нет ни пейзажа на заднем плане, ни рук, да и тень на лице выглядит непонятно. Итого: навыки создания SVG-изображений у новой модели заметно лучше.

Поработав еще с 3.7 Sonnet сразу видна разница — будто обзавелся какой-никакой аналитикой и размышляет перед ответом. Как бы объяснить? Допустим, вы выбираете носки для пробежки. На первый взгляд — просто дело вкуса, так подумает версия 3.5. А 3.7 учтёт всё: от материала до того, как они повлияют на желание выйти на пробежку. Вместо «Пфф, бери, сгодятся. Всего лишь носки», она предлагает вариант, который заставляет задуматься о мелочах и их влиянии даже на такую банальщину.

Давайте выполним первую задачу:

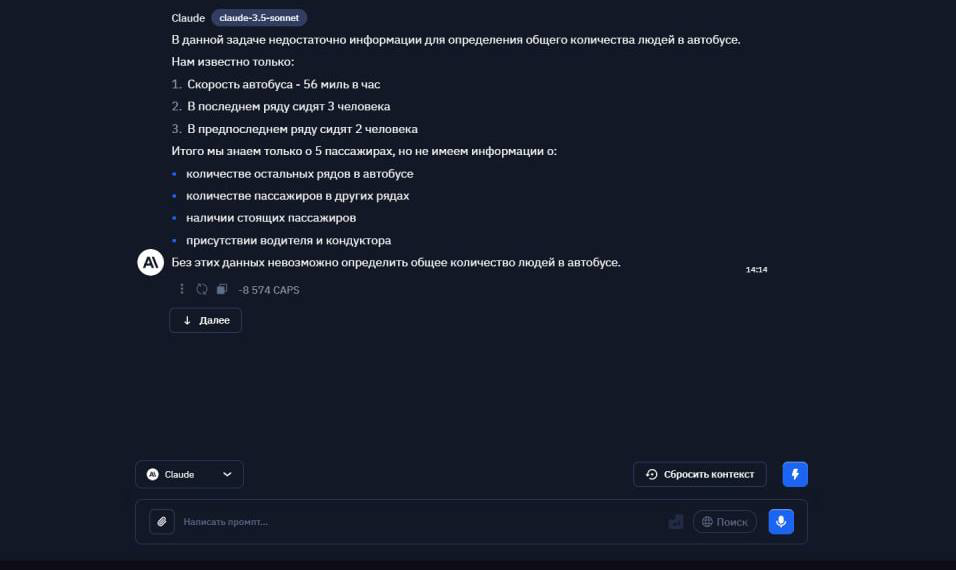
Sonnet 3.5 отказалась решать задачу, но ход мыслей у нее верный. Claude 3.7 явно показала себя лучше: и задачу решила, и учла условности. Ну, и просто, чтобы не обделять, дадим и вторую задачу: а вдруг предыдущая версия решит?

Скрытый текст

1) Построим матрицу смежности a_ij по заданному графу:

U={(1,2),(1,3),(1,4),(2,3),(2,4),(3,5),(4,5),(5,2)}

a_ij = 

| 0 1 1 1 0 |

| 0 0 1 1 0 |

| 0 0 0 0 1 |

| 0 0 0 0 1 |

| 0 1 0 0 0 |

2) Для матрицы полных путей p_ij:

p_ij = I + A + A² + A³ + ... (пока не перестанут появляться новые пути)

I (единичная матрица):

| 1 0 0 0 0 |

| 0 1 0 0 0 |

| 0 0 1 0 0 |

| 0 0 0 1 0 |

| 0 0 0 0 1 |

A² (умножаем матрицу A на себя):

| 0 1 1 1 2 |

| 0 0 1 1 2 |

| 0 1 0 0 0 |

| 0 1 0 0 0 |

| 0 0 1 1 0 |

A³:

| 0 2 1 1 2 |

| 0 1 1 1 2 |

| 0 1 0 0 0 |

| 0 1 0 0 0 |

| 0 0 1 1 2 |

Матрица полных путей p_ij (заменяем все числа >0 на 1):

p_ij = 

| 1 1 1 1 1 |

| 0 1 1 1 1 |

| 0 1 1 1 1 |

| 0 1 1 1 1 |

| 0 1 1 1 1 |

3) Вычисляем ранги:

Для первой строки: ∑_j p_1j = 5

Для первого столбца: ∑_j p_j1 = 1

R_1 = 5/1 = 5

Для второй строки: ∑_j p_2j = 4

Для второго столбца: ∑_j p_j2 = 5

R_2 = 4/5 = 0.8

Для третьей строки: ∑_j p_3j = 4

Для третьего столбца: ∑_j p_j3 = 5

R_3 = 4/5 = 0.8

Для четвертой строки: ∑_j p_4j = 4

Для четвертого столбца: ∑_j p_j4 = 5

R_4 = 4/5 = 0.8

Для пятой строки: ∑_j p_5j = 4

Для пятого столбца: ∑_j p_j5 = 5

R_5 = 4/5 = 0.8

Итоговые ранги:

R_1 = 5

R_2 = 0.8

R_3 = 0.8

R_4 = 0.8

R_5 = 0.8

Вообще, этого следовало ожидать. Что ж, не отчаиваемся и верим, что однажды ИИ сможет решить такую задачку.

Что по программированию на практике?

Заглянем в X, чтобы увидеть, что пользователи создали с новой моделью. 

Пост от 25 февраля: игра «Minecraft». Вроде бы обычный блоковый остров с деревьями, но игрок демонстрирует возможность взаимодействовать с объектами и прыгать. Всё это сгенерировано за один промпт. Конечно, это пока не полноценная игра, но для начала довольно интересно.

Источник: Rowan Cheung

Перед вами игра в стиле Space Invaders. Вышло довольно неплохо. Видно, что есть количество жизней, уровень и значение счета. Смотрю на результат, аж самому захотелось поиграть.

Промпт максимально простой:

Create Space Invader Game

Источник: Marketcalls

Теперь давайте посмотрим на игру в стиле «Супер Марио». Игра неплохая: прыгаешь, собираешь монеты и стараешься не попасть в лапы монстриков. Есть три кнопки для бега и одна для прыжка. Автор отмечает, что Claude справился лучше, чем Grok 3. 

Генерация заняла 2 минуты, а промпт выглядит так:

Create a fully functional 2D Mario game, build it fully playable, with all the features, design, functionality, without any gaps or errors in code.

Источник: Alex Prompter

Кстати о сравнении с Grok 3. Один пользователь протестировал Grok 3 и Claude 3.7, предложив им создать игру с пушками. Визуально обе модели справились, с небольшим преимуществом Claude за его светлые цвета. Однако в игровом процессе Claude 3.7 его разочаровал — пушка не стреляла, не показывала траекторию и не разрушала деревья. Grok 3 с первой попытки сделал работающую пушку, которая стреляла и уничтожала объекты.

Источник: Jorge R.

Давайте теперь создадим свою игру. Я выбрал «Змейку». Но, чтобы не было скучно, играть будет AI против меня. Ввожу промпт:

Напиши игру "Змейка", в которой две змеи соревнуются друг с другом, одной змеёй управляю я, а другой управляет искусственный интеллект.

Давайте посмотрим, что получилось:

Такой результат мы получили с первой попытки. Генерация кода заняла меньше минуты. Всё работает, AI оказался неплохим оппонентом. С трудом обошёл его, и то — в одной игре из трёх.

Что скажу по итогу? Пользователи активно тестируют возможности новой модели для создания простых игр, и результаты пока что варьируются. Надеюсь, что в скором времени Claude проявит себя больше и продемонстрирует улучшения в создании кода. Будем следить за обновлениями!

Резюмируя:

Новая версия действительно хороша: она хорошо справляется с текстами (даже GPT-4.5 далеко до уровня Claude с ее ценником), кодом (правда, не без глупого и неуместного "говнокода" порой, прошу прощения за выражения), считыванием информации из документов и с изображений, задачами на логику.

Тем не менее, как бы хорошо модель ни справлялась с генерацией текста или кода, она остаётся лишь инструментом в руках человека. AI может помочь в процессе, но только человек способен направить его в верном направлении.

Спасибо за прочтение! А что вы думаете насчет новой модели и какие сильные стороны смогли выделить для себя?