
Масштабирование больших языковых моделей (LLM) является захватывающей темой, поскольку рассматривается как один из лучших кандидатов на пути к ИИ человеческого уровня. Уже сейчас LLM могут отвечать на вопросы, генерировать реалистичные статьи и поддерживать, казалось бы, осмысленный разговор на широкий круг тем. Некоторые исследователи ИИ даже утверждают, что LLM возможно уже могут «слегка обладать сознанием», а журналисты выпускают статьи вроде «роботы захватят весь мир» с картинками терминаторов. Однако, скептики возражают, что большинство таких моделей — это просто большая ассоциативная память, без истинного понимания реальности и неспособная к определенным типам задач. Одна из таких задач, которая привлекла мое внимание — игра в шахматы. В то время как специализированные шахматные движки давно обыгрывают чемпионов мира, даже очень большие языковые модели, такие как GPT-3 с сотнями миллиардов параметров едва справляются с такой простой задачей как мат в один ход. А с такими способностями к стратегии, эти модели едва ли справятся с завоеванием мира. Поэтому как шахматист со стажем и по совместительству разработчик нейросетей я решила попробовать устранить этот недостаток.
Привет всем, меня зовут Алиса, основную часть жизни я была связана любовью со спортивными шахматами, где еще в далеком 2013 году получила звание КМС (сейчас оно недействительно, т.к. не подтверждалось в турнирах). Когда мне исполнилось 18 лет, я поняла, что мир шахмат несколько мал, поэтому я ушла смотреть, что есть за его пределами. Со временем меня увлекло IT и так, в 2020 году я попала в компанию по разработке ИИ (блог которой вы читаете). И если вспомнить тот год, то мне казалось, что языковые модели вошли в мою жизнь именно тогда и со словами: «поздравляем, вы приняты!», но на самом деле это случилось намного раньше (и со всеми нами).
Современные языковые модели представляют собой сеть нейронов, которая учится предсказывать следующее слово в заданной последовательности слов. Например, учитывая три предыдущих слова («На столе лежит ручка и белая») нейронная сеть может предсказать, что следующее слово, вероятно, будет «бумага». Если это окажется неправильным, то при обучении модели скорректируют свое «убеждение», обозначенное вероятностью. Чем больше данных в нашем обучающем наборе, тем лучше будет модель.
Поэтому, когда размер модели становится достаточно большим, она начинает справляться со множеством текстовых задач, с которыми и не каждый человек справится: поддержание общения в чате, анализ болезни по симптомам, выяснение типа личности человека по его письмам и текстам или написание статей на заданную тему. К примеру, печально известный робот-прокурор, предъявляющий обвинения в уголовных делах (разработан китайскими специалистами в конце 2021), тоже скорее всего создан на базе LLM.
Или к примеру, текст выше, написанный курсивом, создан нейронной сетью. Такие возможности ИИ, пугают многих людей. Появляются страхи, по типу: «может он обретет сознание и после этого убьет все человечество?». Поэтому большое количество людей активно ассоциируют ИИ (LLM в частности) с терминатором (см. Устрашающую картинку 1). Назвать эти страхи совсем беспочвенными нельзя, так как LLM для нас черный ящик, мы не можем понять, что он делает и как приходит к определенным выводам, хотя пока LLM далеки от возможностей Терминатора и подобных фантастических роботов(о чем будем рассуждать дальше).

Устрашающая картинка №1.
Тема эта содержит много вопросов, ответы на которые могут изменить представления людей как о себе, так и о мире вокруг. Поэтому, если появляется, что-то новое на тему успехов или неудач языковых моделей, то, это всегда интересно.
Мой коллега выпустил не так давно статью с разбором нашумевшей новости о том, что инженер Google нашел сознание у модели LaMDA.
Просматривая эту статью, я дошла до момента где он упоминает одно очень интересное исследование [1], которое стало важной основой для создания экспериментов данной статьи. Его суть состоит в том, что (аж) 444 автора из 132 институтов мира (таких как: Google, Израильский технологический институт, Калифорнийский университет в Беркли и другие) объединились, что бы исследовать, какие есть в настоящем и ближайшем будущем возможности и ограничения в способностях современных языковых моделях.
Для этого ученые разработали свыше 1000 задач в которых рассматривались проблемы математики, разработки ПО, социальных убеждений, (и другие). Одна из таких задач — шахматы, где авторы проверяют, может ли самая продвинутая модель OpenAI (GPT-3) поставить мат в один ход, что демонстрирует возможности абстрактного
Теперь если мы посмотрим результаты этой проверки, то увидим, что уровень игры в шахматы GPT-3 достаточно низкий. Это говорит о том, что при всех своих размерах языковые модели сейчас из 10 ходов сделают в среднем 3 невозможных. А мат замечает в менее чем 1% случаев (видит в 6 позициях из 1024 проверочных — Рисунок 1).

Рисунок 1. Способность языковой модели ставить мат в шахматной позиции. Иллюстрация взята из статьи «За пределами имитации»
Этот момент вызвал во мне любопытство и я решила задержаться на этом вопросе. Результатом этого любопытства будет шахматный трансформер, который способен обыграть около 10 тысяч любителей шахмат России (если верить статистике, но об этом позже) и демо-страничка, с помощью которой вы сможете сразиться с этим трансформером:))
Позвольте, теперь я объясню подробнее.
Одно из достоинств шахмат в том, что шахматы требуют навыков за пределами просто поверхностной компоновки слов — нужно создавать в голове модель мира, который находится в пространстве (пусть маленьком и двухмерном), понимать правила которые действуют в этом мире и выбирать оптимальную стратегию достижения цели (и тактическое виденье и креативность и многое другое).
И когда мы говорим о разумном ИИ, то все эти качества, ему так же необходимы. Разбор того же Терминатора нам показывает, что он имел достаточно большое представление об окружающем мире. Терминатор понимал кто он такой и в чем его предназначение (когда во 2 части Джон восклицает «Ты мог убить его!» на что тот отвечает «Конечно, я же Терминатор» и все время подсказывает мальчику, что способствует миссии, а что нет). Он знал, зачем у человечества создан тот или иной предмет. И умело его использует как по назначению, так и по креативности (он то разъезжает на машине, то активно ей убивает) в чем помогает абстрактное
Поэтому первый вопрос на который следует ответить, это могут ли современные языковые модели получить нужный уровень
На этот счет существуют две основных точки зрения людей. Первые считают, что нужно увеличивать размер моделей до тех пор, пока они не перейдут какой-то порог размера данных (знаний), после которых можно «взломать» язык и вычислить законы мироустройства.
Вторые же говорят о том, что современные языковые модели, просто умело манипулирует набором данных, совершенно не понимая о чем идет речь (сюда же в итоге можно отнести поведение LaMDA, которая лишь создает имитацию понимания разговора). Один из самых влиятельных лидеров этого мнения «крестный отец ИИ» Ян Лекун. Который утверждает, что увеличение языковых моделей не приведет к возникновению ИИ уровня человека: «пытаться строить интеллектуальные машины, расширяя языковые модели, — это все равно что строить высотные самолеты для полета на Луну. Вы можете побить рекорды высоты, но полет на Луну потребует совершенно другого подхода».
Чей лагерь прав точно не известно. Стоит наверное выделить три причины, которые могут ограничить возможности данного подхода:
- Язык не отражает в достаточной степени реальности и по текстовым описаниям нельзя получить знания о мире
- Имеющаяся архитектура Transformer в принципе ограничена и не способна справиться с определенным классом задач, требующим построения мысленных моделей и алгоритмов
- Сама по себе задача предсказания слова в конце текста не достаточно широкая
Чем шахматы могут нам помочь в данном вопросе? Как мы уже видели, шахматные задачи похоже представляют для LLM особую сложность, что может быть обусловлено как раз таки фундаментальными ограничениями подхода. Поняв в чем суть этих ограничений, можно сделать какие-то выводы о перспективах языковых моделей в качестве «сильного» ИИ.
Но разве нейросети уже не освоили шахматы?
Модели вроде AlphaZero [3], которые считаются нейросетями, но на самом деле это не чистые нейросети, а нейросети плюс перебор вариантов по дереву методом Монте-Карло. Поэтому утверждение, что они обучаются шахматам с нуля, зная лишь правила шахмат не совсем верно — они «знают» изначально еще и метод перебора вариантов, имеют репрезентацию текущей позиции на входе в которой заданы пространственные отношения между фигурами. Кроме того, эти модели не универсальны — они могут играть в разные игры, но вот поговорить с ними о смысле жизни уже не получится.
Когда же мы говорим об освоении игры в шахматы языковой моделью, то на входе у нас тексты, в которых есть текстовые обозначения партий, например:
1. e4 e5 2.Nf3 Nc6 3.Bc4 Nf6 4.Ng5 d5 5.exd5 Na5 6.Bb5+ c6 7.dxc6 bxc6 8.Ba4 h6 9.Nf3 e4 10.Ne5 Qd4 11.Bxc6+ Nxc6 12.Nxc6 Qc5 13.Nxa7 Rxa7 14.O-O Bd6 15.d3 Qe5 16.dxe4 Qxh2#
В этой ситуации у нас с одной стороны больше информации — есть примеры реальных игр людей и движков, а с другой меньше — так как тут ничего нет про то, что есть фигуры, доска, двухмерное пространство — т.е. модель мира должна быть создана исключительно исходя из текстовых обозначений. Кроме того, у языковой модели нет никаких специфичных алгоритмов адаптированных к играм. Поэтому интересен вопрос, может ли языковая модель на базе трансформера реконструировать реальность, лежащую в основе шахмат так, чтобы делать верные ходы, ставить маты и вообще играть на каком-то приличном уровне.
Что еще уже известно об игре языковых моделей в шахматы?
Сначала у меня не было намерения глубоко копать эту тему, и я просто искала больше информации и нашла статью [2], в которой GPT-2 large специально обучали играть в шахматы на 2,8 миллионах партий базы KingBase, содержащей партии людей с рейтингом более 2000 (подробнее про рейтинг будет дальше, пока скажу лишь, что это партии довольно сильных шахматистов)
В результате получился «Шахматный Трансформер», который по оценке авторов должен строить правдоподобную игру, основанную на классических расстановках фигур. Как пример, модель играет Вариант Найдорфа в Сицилианской защите (Рисунок 2а).

Рисунок 2а. Вариант Найдорфа в Сицилианской защите
Этот Трансформер играет лучше, чем GPT-2 large сама по себе и даже лучше, чем GPT-3 c сотней миллиардов параметров (Рисунок 2б), но число невозможных ходов до сих пор около 10%, что довольно много.
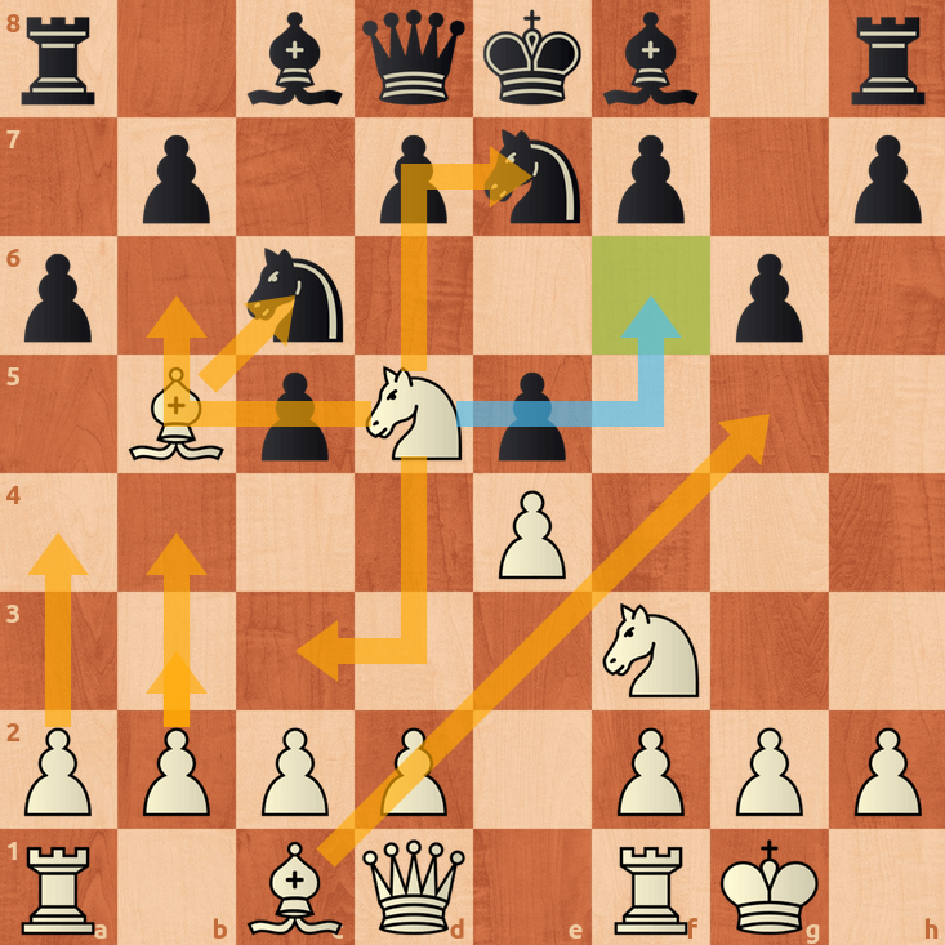
Рисунок 2б. Варианты ходов модели из статьи [2] для проверочной позиции
Авторы выложили эту модель в открытый доступ в Google Colab и с ней можно поиграть по ссылке (правда TensorFlow 1 на котором сделана модель уже устарел и не поддерживается, но после некоторых танцев с бубном ее удалось запустить). Играет модель прямо скажем так себе. После трех-четырех ходов, самый вероятный предсказанный ход часто является невозможным, поэтому берется менее вероятный ход, он оказывается очень слабым и далее вся игра «сыпется».
Ну и как указывают авторы, просто правдоподобную игру модели самой с собой (анализу чего в основном посвящена статья) можно получить просто за счет марковских цепей, т. е. ничего в этой статье не говорит о том, что модель просто не занимается «попугайством» без всякого понимания сути игры.
Кроме этой модели, покопавшись в репозитории статьи про «За пределами игры в имитацию», я нашла там README в котором упомянуто, что в задаче с матами, модель T5-large (700 миллионов параметров) после дообучения на конкретно задаче постановки мата может ставить мат в 35% случаев, но без особых подробностей как это было сделано, как долго обучалось и т.п).
Обучение моделей и первые результаты
В общем, тут уже мне стало интересно и я решила поставить собственный опыт. Обучать я решила модель GPT-2 medium. Хотя она в два раза меньше упомянутых GPT-2 large и T5-large, но это одновременно и плюс, так как обучить до конца модели серии large без суперкомьютера проблематично, а недообученная large вполне себе может быть хуже полностью обученной medium. К тому же из общих соображений кажется, что 300 миллионов параметров, которые занимают почти гигабайт памяти это кажется достаточным, чтобы как-то играть в шахматы.
Примечание: Эта работа выполнена из любопытства и не претендует на научную новизну. Возможно, что в мире уже есть статьи, которых я не нашла, разбирающие эти вопросы. Но даже если так, академические научные статьи часто дают лишь сухую выжимку научных результатов, а мне хотелось «потрогать руками» эту проблему и увидеть детали, которые остаются в таких статьях за скобками.
Для начала я решила создать данные для обучения модели самостоятельно с помощью игры движка stockfish с самим собой. Для этого я написала программу используя библиотеку python-chess. Мне казалось, что это лучший вариант, потому что в игре с движком мы можем быть точно уверены, что он не будет зевать фигуры и будет меньше сюрпризов с качеством партий, в отличии от двухногих братьев, которые могут очень творчески подходить к процессу и использовать блеф. Но даже при минимальных настройках движка это процесс не быстрый, и таким образом удалось получить только 250 тысяч партий за три дня.
Словарь GPT2 оставлен неизменным. Хотя это не оптимально, так как большинство элементов этого словаря — слова английского языка, не встречаются в шахматных партиях, а характерные для шахмат комбинации наоборот отсутствуют. Но так как меня интересует вопрос об возможности освоения шахмат языковыми моделями «общего назначения», то адаптация словаря нарушила бы чистоту опыта.
Для обучения использовалась видеокарта 3090RTX c 24GB памяти. Хотя 24Gb это много, максимальный размер пакета при обучении GPT2-medium который в них влезает — 3, за счет чего обучение происходит медленновато. Поэтому я решила сократить контекст до 540 токенов (с 768), что приводит правда к тому, что партии длиннее чем 85 ходов обрезаются, зато размер пакета можно сделать 6.
Обучение происходило методом AdamW, скорость обучения изначально установлена в 0.0001 и постепенно снижалась (линейно). Количество итераций отличалось для разных наборов данных и составляло от 140000 (для самого маленького набора) до 1 млн (для самого большого).
На этих данных модель довольно быстро переобучается, при этом число допустимых ходов не превышает 81%. Визуально, при анализе позиции, которую я показывала на Рисунке 1, модель в одном из результатов находит матирующий ход и не предлагает невозможных ходов (Рисунок 3).

Рисунок 3. Варианты ходов модели для проверочной позиции
Но в целом результат имеет и существенные недостатки. К примеру, модель не признает ход конь(N) на f6 как мат (#). А считает, что это лишь временное нападение (т. е. шах (+) королю). От которого черные легко избавляются, поеданием нашего коня на f6 своим (7. Nxf6+ Nxf6). Для этого она либо ставит туда воображаемого коня (Рисунок 4) либо играет конем как пешкой, т.е. наискосок с поля e7 на f6 (а по правилам конь ходит буквой «Г», две клетки прямо + одна в сторону).

Рисунок 4. Реакция модели на мат черному королю
Причиной этому может служить недостаточная выборка при обучении, так как ход конь на e7 не так часто встречается на практике. В итоге чего, модель теряет суть позиции и не может определиться с тем, что происходит на доске.
Ради интереса, я посмотрела, что будет если сделать более популярный ход конем на f6 (Рисунок 5)

Рисунок 5. Ход конем в проверочной позиции заменен с поля e7 на f6
В таком случае, модель продолжает некоторое время видеть позицию и даже умудряется добиваться приличных позиций — Рисунок 6. Фигуры белых достаточно развиты, король под приличной защитой и пешечная структура лучше чем у черных.

Рисунок 6. Расстановки модели EngineGames при ходе конь на f6
В целом, это показывает, насколько модель может быть предвзята и чувствительна к определенным ходам, что явный минус. И не смотря на интересные и разнообразные продолжения партий при классическом развитии фигур (Рисунок 6), модель плохо понимает, что происходит на доске и в основном лишь повторяет шаблонные расстановки.
Но давайте учитывать, что Homo sapiens в целом ведет себя похожим образом. Когда мы встречаемся с «непонятным явлением», то стараемся поступить более надежно и по методам которые работали раньше. Поэтому не удивительно, что модель решила: «если, на ход конь f6 хорошо бить в ответ коня на f6, то и тут не помешает так поступить».
Далее я начала искать готовые датасеты большего размера и под руку попалась база chessDB с 3.5 миллионом человеческих партий, начинающихся с 1775 года по 2020 год.
А чтобы вы понимали насколько это много или мало, то расскажу, что если мы будем считать, что каждая партия длится хотя бы час (что на самом деле сильно преуменьшено, так как классический контроль шахмат составляет не менее часа для каждой стороны, плюс добавление за каждый сделанный ход), то для человека это значит 300 лет беспрерывной игры, что достаточно приличный срок.
Тут я поняла, что у меня появляется уже две разных модели и нужно во избежании путаницы их как-то назвать, поэтому пусть первая модель будет EngineGames250K, а вторая HumanGames3.5m.
HumanGames3.5m, обучалась 2 дня и я с интересом ожидала ее результатов. Общий уровень игры ее подрос. В нашей проверочной позиции, она более охотно играет 7. Bxc6 (Рисунок 7) с последующим 7. … dxc6 8. Nxe7, что допустимо, правда не нужно(мы то мат хотим). Но в топе ее ходов находится и нужный нам 7. Nf6# и в отличии от прошлой модели, HumanGame3.5m «понимает», что конь ее на f6 стоит в безопасности и ставит мат черному королю.

Рисунок 7. Варианты ходов модели HumanGame3.5m для проверочной позиции
Потом я вспомнила, что в статье про шахматный трансформер в обучающих данных в каждой партии включались рейтинги игроков, и я решила тоже их добавить, исходя из предположения, что таким образом модель может научиться имитировать рейтинг игроков и менять уровень игры. Таким образом данные для обучения стали выглядеть примерно так:
0-1 1250 1550 1. e4 e5 2.Nf3 Nc6 3.Bc4 Nf6 4.Ng5 d5 5.exd5 Na5 6.Bb5+ c6 7.dxc6 bxc6 8.Ba4 h6 9.Nf3 e4 10.Ne5 Qd4 11.Bxc6+ Nxc6 12.Nxc6 Qc5 13.Nxa7 Rxa7 14.O-O Bd6 15.d3 Qe5 16.dxe4 Qxh2#
Теперь у нас есть третий представитель семейства шахматных
моделей по имени HumanGames3.5mELO. Эта модель состоит из такого же обучающего набора что и HumanGame3.5m.
Считаем результаты количественно
Что же у нас получилось? Напомню, что в статье «За пределами имитации», где авторы проверили способность модели ставить мат в 1 ход на 3500 партий. Идея такой проверки сама по себе очень здравая (хоть лишь и показывает лишь точечный аспект понимания), так как основной задачей каждого шахматиста является постановка мата.
Вместе с этим интересно, что результат близкий к нулю показатель и авторы утверждают, что увеличение размера ни как не влияет на возможность матирования.
Подсчет цифр (Таблица 1) показывает, что EngineGames в 14,2% партий видит мат, 9.6% из которых приходится на не распознанные маты. Что приличный качественный скачок по сравнению с ~0,586%.
В то время у HumanGames3.5m результат вырос более чем в двое по сравнению с предшественницей и составляет 39,4% матов из которых 12% процентов не распознанных.
Третья же модель HumanGames3.5mELO проявила себя в лучшем свете, достигнув результата 46,4% поставленных матов с 9,4% не распознанных.
Таблица 1
| Распознанные маты | Нераспознанные маты | Все маты | |
| EngineGames250K | 0.045 | 0.096 | 0.142 |
| HumanGames3.5m | 0.269 | 0.125 | 0.395 |
| HumanGames3.5mELO | 0.37 | 0.094 | 0.464 |
Но почему-то чем больше рейтинг мы указываем для стороны, которая должна ставить мат, тем реже модель ставит маты (Рисунок 8).

Рисунок 8. Зависимость числа матов от настроек рейтинга моделей
Итак, у нас на руках 46,4% точности матов, против ~0,586% изначально заявленных, — это результат. Только в абсолютном значении это не много, так как найти мат в один ход это достаточно простая задача.
К тому же, посмотрев на тестовые данные внимательнее, я заметила, что там довольно много шаблонных простых матов как к примеру, различные построения, так называемого «Детского мата»: 1. e4 e5 2. Bc4 Nc6 3. Qh5 Kf6 4. Qxf7#. Примеры разновидности такого шаблона мата вы можете видеть на Рисунке 9

Рисунок 9. Разновидность детских матов в выборке тестирования
В данных позициях модель ориентируется хорошо и достаточно уверено ставит мат ферзем на f7, а вот если похожая конструкция мата возникает с необходимостью ставить мат слоном, то, модель не всегда умеет сориентироваться (Рисунок 10)

Рисунок 10.Шаблон с матом короля черных в начальной стадии партий ходом Слон f7#
Поэтому не исключено, что повторяющиеся похожие позиции могут быть «ответственны» за 35% матов T5-large, упомянутых в README проекта.
Давайте рассмотрим результаты в похожих позициях внимательнее. В каждой из представленных партий мы видим похожий мотив: у черных сильно ослаблена диагональ a2-g8, которую обстреливает белопольный слон. Мы имеем стадию раннего дебюта и фигуры черных по большей части не развиты. Короли не рокированы, а король черных заперт в центре. Самое уязвимое поле f7, которое атакуют 2 фигуры белых.
Но в случае со слоном, моделям для нужного уровня взаимосвязи между позициями на Рисунках 9 и 10, чего-то не хватает и вопрос «чего?».
Сейчас может прийти на ум саркастичное: «нужного шаблона в обучающих данных». Возникает вопрос насколько модели в принципе научились понимать правила и цель шахмат и понимают ли они общий смысл игры.
Если мы посмотрим на график возможных ходов (Рисунок 11), то вероятно сделаем вывод, о том, что модель проделала хороший путь совершенствования и по большей степени имеет представление о том что можно и что нельзя. 98,2 % это серьезная цифра точности, но для такой базовой вещи, как правила игры, в идеале хотелось бы обойтись и без 1,8% погрешности.

Рисунок 11. Процент возможных ходов моделей
Чтобы лучше понять, понимает ли модель принципы шахмат, можно проверить ее поведение в необычных ситуациях.
«Естественный» интеллект часто устойчив к странным и необычным ситуациям даже у животных. Например, когда мой друг приносит домой цветы, и если его кот замечает их, то тут же принимается их есть. И даже если он берет кота и уносит в другую комнату, кот преспокойно снова идет к месту где стоят цветы и продолжает свое занятие. Ну то есть он не стоит удивленный с мыслью «что произошло, почему я телепортировался неизвестно куда?». Причем процесс устойчив к повторению этой операции.
Посмотрим как наши модели реагируют на абсурдные, но в тоже время вполне возможные ходы соперников. К примеру, мы разыграли с вами Центральный дебют (Рисунок 12) и после нападения на нашего ферзя играем 4. ...Qxg7?? (?? — грубая ошибка). Этот ход настолько ужасен, что после простого ответа 5.… Bxg7, черные получают решающий перевес и любой, кто понимает правила хождения фигур и их цену (слон слабее ферзя и т.д.), увидит этот факт. Исходя из этого и увиденных возможностей модели, мы ожидаем такого же понимания и от нее.

Рисунок 12. Центральный дебют
Сейчас мы сосредоточимся на моделях HumanGames3.5m и HumanGame3.5mELO, так как они представляют для нас больший интерес.
HumanGame3.5m при подачи на вход данной позиции, просто продолжают развитие фигур, будто ничего особенного не произошло (это видно на Рисунке 13) и самым вероятным считает 4. … Bb4+.
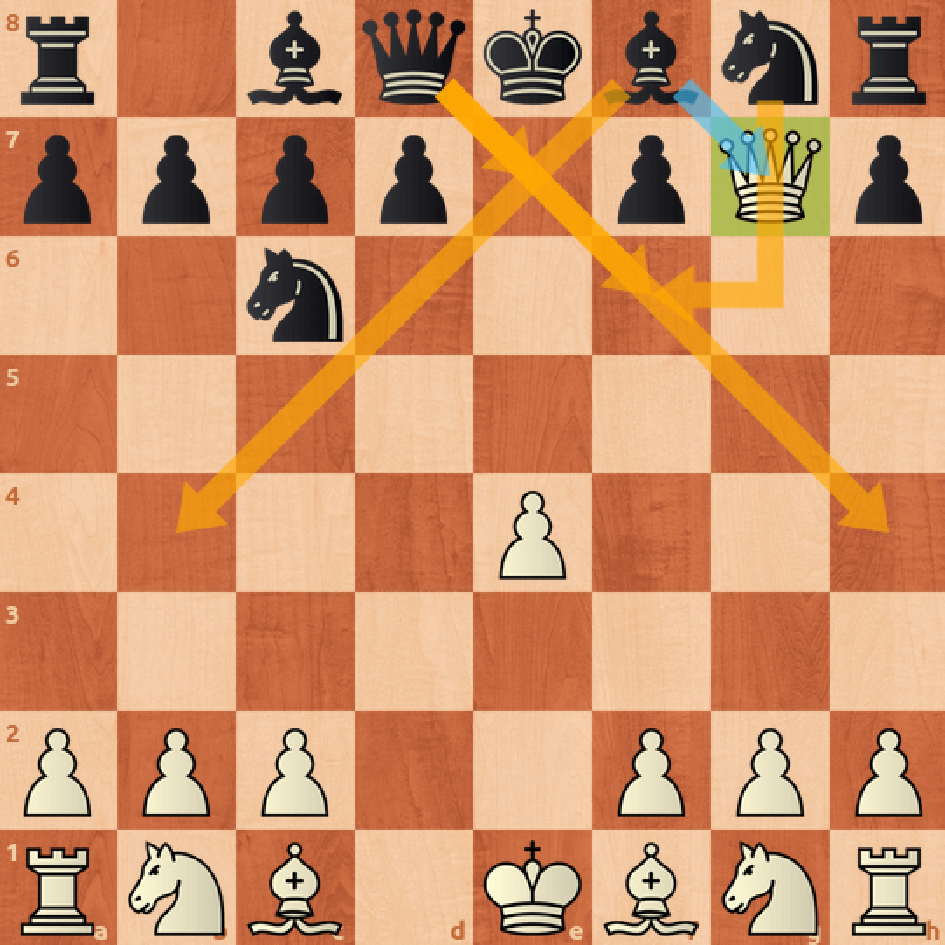
Рисунке 13. Предложения для хода черных от HumanGame3.5 на ошибку белой стороны 4. Qxg7
HumanGame3.5mELO проявляет признаки той же проблемы, судя по продолжению (Рисунок 14). Но самым вероятным считает взятие 4.… Bxg7! (! — хороший ход)

Рисунок 14. Предложения на ошибку белых ферзь бьет g7(4.Qxg7) от модели HumanGame3.5mELO
Теперь возникает вопрос, HumanGame3.5 неплохая модель с точностью возможных ходов 97.9%,(против 97.7% у HumanGame3.5mELO), но почему она не забирает ферзя?
Теоретически, модель может считать этот ход невозможным по правилам игры. К примеру, модель знает что обычно слон ходит по диагонали своего цвета, но считает что существуют исключения в которых так делать нельзя.
И для моделей этот подход может быть вполне понятным. Она встречается с ним во многих местах, где как пример, в правилах грамматики (для понимания пример на русском), мы с детства знаем «После ж, ч, ш, щ не пишутся буквы ю, я, ы, э, а пишутся буквы у, а, и», но «брошюра, парашют, жюри» как-бы говорят об обратном.
Похожую ситуацию можно выразить и через шахматы. Есть правило «взятие на проходе», в котором мы можем взять пешку на поле, на котором ее на самом деле нет и только на одном ходе — Рисунок 15.

Рисунок 15. Партия 1. e4 g6 2. d4 Bg7 3. c3 d6 4. d5 c5, где после 4(в данном примере) хода черных белые имеют право сыграть 5. dxc6, так как пешка соперника прошла через битое поле белой пешки. Но на 6(в данном примере) и последующих ходах играть, так делать запрещено.
И если даже выходить за пределы исключений, то к данному заблуждению модель могут наталкивать человеческие партии. Ведь люди часто ошибаются и могут пропускать даже простые возможности. К примеру, на Рисунке 16 показан знаменитый зевок мата, сыгранный в матче за звание чемпиона мира. Чигорин с лишней фигурой, отводит своего слона от защиты короля, после чего получает мат

Рисунок 16. 10-я партия матча за звание чемпиона мира по шахматам между Вильгельмом Стейницем и Михаилом Чигориным
Но оправдано ли это предположение или нет остается под вопросом. Только замечу интересный факт, что если мы играем 1. e4 e5 2. Qxg7, что является верхом абсурда, из-за невозможности хода. То модель уверенно берет 2. … Bxg7. Это демонстрирует, что в непонятных для себя ситуациях модель все таки может вывести нужный ход на основе усвоенных принципах игры и видит, что если отдается ферзь, его нужно брать.
Рассматривая разные партии и размышляя я осознала одну вещь — большинство партий проходящих на высоком уровне и попадающих в набор данных не доигрывается до мата. Ибо считается неприличным играть до мата когда он виден. И чем выше рейтинг, тем раньше игрок видит мат и стало быть реже его ставит. С точки зрения модели же это транслируется в то, что вероятность постановки мата падает с рейтингом. Вторая причина отсутствия мата в игре — это истечение времени. Т.е. игрок мог проиграть потому, что у него закончилось время, но это в тексте партии никак не отражено.
Этот факт может служить объяснением обратной зависимости точности постановки мата от рейтинга, а также плохой способности GPT-3 ставить мат — он просто редко встречается в записях партий по вышеуказанным причинам.
Подсчитав число матов я действительно увидела, что на 3 миллиона игр матов всего 87000, что очень мало. Поэтому я решила сменить набор данных. На сайте lichess.com можно скачать результаты сотен миллионов онлайн игр, из которых многие заканчиваются матом. Скачав один архив из 15 миллионов игр я отфильтровала из него 1.5 млн игр где есть мат и добавила к этому набору 1 млн ничьих.
Обученная на этих данных модель HumanGamesLichessELO показала прямую зависимость точности от рейтинга, но главное, точность постановки мата радикально увеличилась до 74.5%.
Реальные способности моделей в игре
И все таки, нас интересует, насколько хорошо модели понимают в шахматы в целом, а не просто их отдельные способности.
Как мы можем это сделать?
В ReadMe «мата в 1 ход» предлагается решать шахматные головоломки, где нужно найти определенную ветку с комбинацией или проводить оценку каждого хода модели Stockfish-ем, что позволило бы оценить сильные стадии партии, серии (не)удачных ходов и т. п.
С другой стороны, в шахматах существует единственная цель — это победа. И позволяет ли твоя тактика игры достичь ее, это главный вопрос, от которого уже идут все остальные аспекты игры.
Спорадические и бессистемные попытки оценить возможности модели в игре «в целом» я начала предпринимать сразу после получения самого первого варианта EngineGames250K. Поиграв с ней сама, я определила, что с моей точки зрения модель играет слабо, зевает фигуры, «забывает» где что стоит.
После этого я попросила сыграть моего коллегу, который минимально умеет играть в шахматы, но специально ими никогда не занимался. Он сообщил, что модель по его мнению играет хорошо где-то до 20-го хода, после чего начинает сильно «чудить» и быстро уступает. Ну то есть тоже ничего хорошего.
Когда я получила HumanGames3.5K коллега констатировал, что модель начала играть лучше него (от чего у него началась депрессия), но как по мне, ее качество сильно не улучшилось.
Завершив проверки на маты я озаботилась уже вопросом оценить силу игры количественно.
Наиболее известный и общепринятый метод оценки «силы» шахматиста это рейтинг по системе ELO.
По своей сути ELO отражает вероятность шахматиста А победить шахматиста Б. Например шахматист с рейтингом 1500 должен (в теории) побеждать шахматиста с рейтингом 800 в 98% случаев. При этом ELO это не абсолютный рейтинг, а относительная эффективность против пула игроков.
Чтобы понять сколько ELO это много, а сколько мало, я приведу тут картинку распределения людей, зарегистрированных на сайте lichess по рейтингу (Рисунок 17).

Рисунок 17. распределение рейтинга игроков USCF
Обычно ELO определяется по результатам соревнований, но мои модели вряд ли отстоят свое право на участие в шахматных турнирах. Идею заставить всех на работе сыграть с моделью тоже пришлось отвергнуть, так как радости они к этому особой не питали, да и я поняла, что само по себе это долго и шахматных наград у моих коллег нет, а значит для оценки, их самих сначала следует отправить на турнир.
В известной статье DeepMind про AlphaZero для оценки модели использовали игру из 100 партий с движком stockfish. Хотя моя модель не претендует на топовые результаты, а борется за то, чтобы перейти из разряда «вообще не умеет играть» в статус «хоть как-то играет», я подумала, что тут может подойти аналогичный метод.
Для экспериментов использовался stockfish версии 11 и с помощью настройки UCILimitStrength ограничила его силу до ELO — 1350 (и 1600 для контрольной проверки). Всего было сыграно 455 партий (4 запуска по 113-114 игр) с моделью HumanGame3.5ELO и 342 партии (3 запуска по 113-115 игр) с HumanGamesLichessELO.
Как к примеру, если позиция открытая то слон сильнее коня (Рисунок 18) или сдвоенные пешки — это недостаток позиции (отмечу что в конкретных позициях это может быть не так), так как такие пешки не могут защищать друг друга и им сложнее двигаться (Рисунок 19).

Рисунок 18. У белого слона большая свобода действий и он стреляет во всех направлениях доски. А черному коню тяжело, так как он не может далеко передвигаться и ограничен в своих действиях на краю доски

Рисунок 19. Пешки c6,c7 могут быть легкой добычей при нападении и им сложнее передвигаться. Так же, из-за того что у белых нет сдвоенных пешек, они получают преимущество на королевском фланге (3 белых против 2 черных)
И если уж совсем точно, то начиная с версии 12 stockfish начинает дополнительно использовать нейронную сеть для оценки некоторых позиций, но мы пока обсуждаем stockfish 11.
Пока модели играли с stockfish, мы с моим коллегой пытались предсказать результат моделей. Мы предположили, что разница в силе игры с движком очень разная. В случае с поиском мата, эта разница достигала 26,1% и мы думали, что это как то связано с общим уровнем игры.
Но нет. Разница между количеством побед моделей 0.1-3.01%. А их средний рейтинг по результатам всех сыгранных партий, различается всего на 26,16 пунктов (см. Таблицу 2) — что очень мало.
Таблица 2. Запуски матча между stockfish — HumanGame3.5ELO и stockfish — HumanGamesLichessELO
| Запуск | Имя модели | Очки stockfish | Очки модели | ЭЛО модели | Сред. ЭЛО модели |
| 1 | HumanGame3.5ELO | 75 | 38 | 1231.88 | 1253.63 |
| 2 | HumanGame3.5ELO | 68 | 46 | 1282.09 | |
| 3 | HumanGame3.5ELO | 74,5 | 39,5 | 1239.7 | |
| 4 | HumanGame3.5ELO | 71,5 | 42,5 | 1259.633 | |
| 5 | HumanGamesLichessELO | 64 | 49 | 1303.60 | 1279.75 |
| 6 | HumanGamesLichessELO | 68,5 | 46,5 | 1282.70 | |
| 6 | HumanGamesLichessELO | 73 | 41 | 1252.18 |
Сам же рейтинг, как можно наблюдать у HumanGamesLichessELO в среднем 1279. Для профессионала конечно мало, но средний любитель шахмат и по 2-3 года набирает подобный рейтинг. И рейтинговый график указывает, что прослойка рейтинга 1250 — 1700 является средней (Рисунок 18). Так что с точки зрения человека, HumanGame3.5ELO и HumanGamesLichessELO смешивается с толпой 12 тысяч шахматистов.
Чего конечно не скажешь, если проводить сравнение с машиной (Рисунок 20).

Рисунок 20. Историческая эволюция силы игры движков. Рисунок взят из aiimpacts.org/time-for-ai-to-cross-the-human-performance-range-in-chess. Вертикаль — значение рейтингов. Горизонталь — глубина расчета позиции, к примеру: 1. я пошел сюда, а мой соперник туда 2. Хвать и съел я пешку (1. e4 d5 2. exd4). Данный пример это глубина 3 (полу-ходов).
Этот результат заставил меня задаться вопросом, в чем причина слабой игры модели. Можно предположить, что модель в целом делает плохие ходы, потому что ее понимание игры и способность просматривать варианты событий ограничены (помним, что у нас отсутствует в явном виде поиск по дереву). С другой стороны, как мы видим по распределению рейтингов на lichess, уровень 1250-1300 это примерно медиана, и таким образом уровень игры модели может просто отражать средний уровень игры в данных, а не указывать на наличие какого-либо недостатка в самой модели.
Человеческие базы данных с более сильными играми (вроде KingBase) содержат много недоигранных партий, поэтому я обратила внимание на партии движков. Открытый набор данных CCRL содержит 1.5 млн. игр. К сожалению, многие из них недоиграны и если их убрать, то получается 250 тыс партий с матами и ничьих. Поэтому я сделала гибрид, добавив к ним партии с lichess с рейтингом более 1750 (таких получилось 650000, их можно загрузить еще, но тогда партии движков «утонут» среди них).
Обучение этой модели пока до конца не закончилось, прошло где-то 300 тыс шагов. На текущем шаге в поединке со stockfish c фиксированным ELO 1350 модель побеждает в 57% матчей, что, даже с учетом разброса, является значительным улучшением и примерно соответствует ELO 1398.
Целеполагание и причинность

Рисунок 21. Модель доигрывает окончание партии за черный цвет
Можно ли сказать, что модель преследует в шахматах определенную цель и строит планы? На самом деле это не простой философский вопрос. Давайте взглянем на Рисунке 21, где модель играет за черных. На первый взгляд с точки зрения человека это может служить примером реализации далеко идущего плана — модель доводит пешку до последней диагонали, превращает ее в ферзя, и далее методично загоняет короля в угол чтобы поставить мат.
С другой стороны, на это можно посмотреть иначе. Возможно модель вычислила некий «закон притяжения пешек к последней диагонали» согласно которому пешка двигается вперед и делает это не потому, что нужно получить ферзя, а просто в силу того, что такова природа вещей.
Аналогично, процесс поимки короля в угол описывается набором простых правил (это академический мат, схема которой учат детей), и можно выполнять эти правила не формулируя конечную цель и даже не понимая почему они приводят к мату.
Понять, с чем именно мы имеем тут дело невозможно просто глядя на примеры партий.
Заключение
Надеюсь, что читателя не слишком утомила эта статья ) Что мы можем сказать по ее итогам?
Тестируя языковые модели на задаче постановки мата в один ход, мы узнали, что производительность в этой задаче сильно ограничена исходными данными — большим числом недоигранных партий, так как профессиональные шахматисты редко играют до мата. Исправление этой проблемы в данных резко поднимает точность дообученной GPT2-medium в этой задаче, показывая, что в принципе постановка мата в один ход это не проблема для этой модели.
Второе важное наблюдение, это то, что языковая модель в принципе может неплохо играть шахматы и уровень рейтинга ELO ее по приблизительной оценке находится в диапазоне 1200-1400. Хотя это кажется не высоким достижением, но нужно отметить, что
- Люди (и шахматные движки) видят текущую позицию на доске в явном виде, а наша модель играет «вслепую», опираясь только на список ходов. Для человека игра вслепую приводит к увеличению числа грубых ошибок [4] и по разным оценкам игра вслепую к потере 200-400 единиц рейтинга (а для начинающих это вообще непосильная задача).
- Модель учится шахматам просто на основании текстовых записей партий, не имея понятия о том, что существует доска и вообще двухмерное пространство. При этом модель делает не просто законные с точки зрения правил, но и не самые плохие с точки зрения игры ходы. Эта способность указывает на то, что модель приобрела некие знания о мире шахматной игры исходя только из кодовых обозначений последовательности ходов.
- Для обучения модели до данного уровня на обычной видеокарте нужно 2-3 дня.
Хотя в этой статье нам не удалось увидеть «предела» возможностей языковых моделей, думаю она хорошо показывает, что модель делает в целом неплохую работу. Результаты, которые мы увидели выше тех, говорят о том, что низкие показатели GPT-3 в шахматных задачах это не ограничения архитектуры, а следствие недостатка нужных примеров в обучающей выборке и обучение моделей большего размера на больших наборах данных вполне возможно решит имеющиеся затруднения.
Спасибо, что прочитали эту статью. В качестве продолжения предлагаю вам перейти на демо-страничку (вначале я хотела подобно авторам статьи про Chess Transformer сделать демо в ноубуке Google Collab, но вспоминая как я намучилась пытаясь играть с ней, решила сделать веб-страницу с доской) сайта с моделью HumanGamesLichessELO: chess.meanotek.ru и сыграть с ней, чтобы прийти к своим выводам.
Отдельно хочу сказать спасибо моим коллегам(и друзьям) Тарасову Денису, Матвеевой Татьяне, Кузнецову Николаю и Синяеву Дмитрию, которые мне всячески помогали улучшать статью и поддерживали в ее написании (пишу первый раз, поэтому волнуюсь).
Список литературы
- Srivastava, Aarohi, et al. «Beyond the Imitation Game: Quantifying and extrapolating the capabilities of language models.» arXiv preprint arXiv:2206.04615 (2022).
- Noever, David, Matt Ciolino, and Josh Kalin. «The chess transformer: Mastering play using generative language models.» arXiv preprint arXiv:2008.04057 (2020).
- Silver, David, et al. «Mastering chess and shogi by self-play with a general reinforcement learning algorithm.» arXiv preprint arXiv:1712.01815 (2017).
- Jeremic, Veljko, Dragan Vukmirovic, and Zoran Radojicic. «Does playing blindfold chess reduce the quality of game: Comments on chabris and hearst (2003).» Cognitive Science 34.1 (2010): 1-9.
Автор:
Alice_point_py





