Компьютерный покер является весьма нетривиальной задачей в первую очередь из-за громадного количества игровых состояний, которое настолько велико, что мечтать о непосредственном решении этой игры не приходится. Единственным способом хоть как-то научить машину играть в покер является переход к абстракции — уменьшенной копии покера, в которой близкие в стратегическом смысле ситуации исходной игры объединены воедино. Именно вопросам абстракций в покере и посвящена данная заметка.
Данная публикация в какой-то мере отсылается к первой части и предполагает, что читатель знаком с правилами покера. Буду стараться придерживаться популярного стиля изложения, а для интересующихся подробностями есть ссылки на литературу и обсуждение в комментариях.
Зачем нужна абстракция?
Для того, чтобы проникнутся масштабами проблемы компьютерного покера, рекомендую ознакомиться с отчетом [1], где приводятся размеры как лимитных, так и безлимитных покерных дисциплин. Даже для самого «простого» лимитного Техасского Холдема существует ровно 319,365,922,522,608 игровых состояний, в которых нужно принимать решение. В то же время, в этой разновидности покера всего 6378 различных нетерминальных паттернов ставок и все богатство игровых состояний обусловлено именно карточными комбинациями. Для безлимитных и пот-лимитных дисциплин возможностей совершать ставки на десятки порядков больше, чем для их лимитного собрата — в безлимитном Холдеме со стеком в 500 блайндов порядка ~1061 нетерминальных историй. Прочтя вышесказанное, у читателя должно зародиться сомнение в способности современной вычислительной техники решать покер в его непосредственном представлении.
На помощь приходят методы упрощения исходной игры, которые объединяют близкие в стратегическом плане состояния этой игры в неразличимые состояния новой игры, называемой абстракцией. Для покера можно выделить два класса проблем, решаемых переходом к абстракции:
- Проблема ставок в безлимитных и пот-лимитных играх.
- Проблема представления рук игроков.
Ставки и их представление в абстрактной игре
Проблема ставок особо актуальна в пот-лимит и безлимитных дисциплинах покера, хотя сокращать количество паттернов ставок иногда приходится и в лимитных играх с большим количеством игроков. Одним из наиболее популярных приемов тут является дискретизация ставок, когда диапазоны ставок разбиваются на интервалы и все манипуляции в дальнейшем осуществляются со ставками, привязанным к диапазонам.
Рассмотрим вариант дискретизации для безлимитного покера, где ставки определены следующим образом: h — половина банка, p — ставка в банк, d — удвоенный банк, a — ва-банк. Все остальные ставки будем соотносить к ближайшим из вышеприведенных. На первый взгляд такая абстракция ставок вполне адекватна и, действительно, боты использующие ее демонстрируют хороший уровень игры с оппонентами, придерживающимся той же схемы ставок (см., например, [2]). Но если противник вдруг совершит произвольную ставку, сильно отличающуюся от дискретной, то неадекватное поведение бота нам обеспечено. Самая очевидная потенциальная уязвимость это совершение оппонентом минимально допустимой ставки, после чего бот может просто сбросить карты. Кроме того, ставки на границах между дискретными диапазонами приводят к принятию ботом «переоцененных» или «недооцененных» решений, что чревато проигрышем денег на дистанции и раскрытием бота человеком. Добавление большего количества дискретных диапазонов не спасает ситуацию, так как увеличивается количество абстрактных игровых состояний и приходится снижать качество абстрактного представления карт.
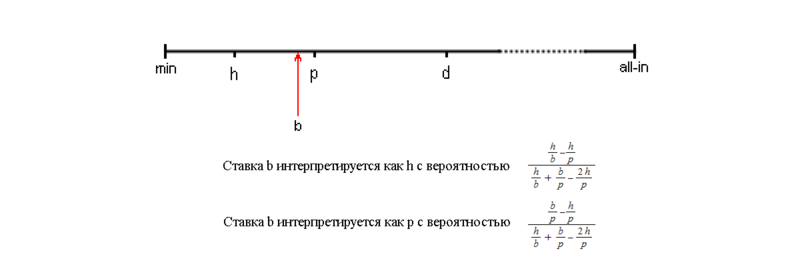
Дискретизация реальной ставки b в абстрактную ставку p в случае «жесткой» трансляции или в одну из абстрактных ставок h и p в «мягкой».
Вышеописанная схема перевода ставок реальной игры в абстрактную получила название «жесткой». Существует и другой, «мягкий» способ транслирования ставок, суть которого заключается в том, что соотнесение реальной ставки к той или иной абстрактной определяется случайным образом, причем, чем ближе реальная ставка к абстрактной, тем вероятность соотнесения выше. В презентации [3] проводится сведения том, что «мягкий» способ трансляции позволяет боту быть менее эксплуатируемым размерами ставок, но при этом и менее прибыльным.
При построении покерного агента, ориентированного на игру с людьми, зачастую дискретизация ставок осуществляется путем анализа реальных игровых раздач, после чего каждому игровому состоянию приписывается своя схема дискретизации ставок. Тем не менее, этот подход по прежнему уязвим после выявления схемы построения абстракции. Дискретизация не является единственным способом представления ставок в покере. Возможен также и подход, который заключен в том, что покерный агент стремится дополнить банк на строго определенную сумму, чтобы привести банк в соответствие со значением, заложенным в абстракции. Очевидно, что такой трюк сразу разоблачает бота и при этом не лишен серьезных недостатков, например, незначительным превышением заложенного размера банка можно вынудить бота сбросить карты.
В последнее время получил развитие способ построения абстракций ставок в покере, при котором вводится еще один игровой агент, принимающий решение о том, какую ставку нужно совершить в конкретной игровой ситуации. В работах [4-5] вместо всех возможных ставок в каждом игровом состоянии игрокам разрешается совершать лишь три: минимальную ставку (L), максимальную ставку (H) или же уйти в ва-банк. При этом решение о том, какую из двух ставок L или H нужно сделать принимает новый игровой агент. Очевидным преимуществом такого подхода является сложность эксплуатации бота размерами ставок, но при этом появляются вопросы, связанные с обучением нововведенного агента, нахождением конкретных значений для ставок L и H, организацией представления абстракции в целом.
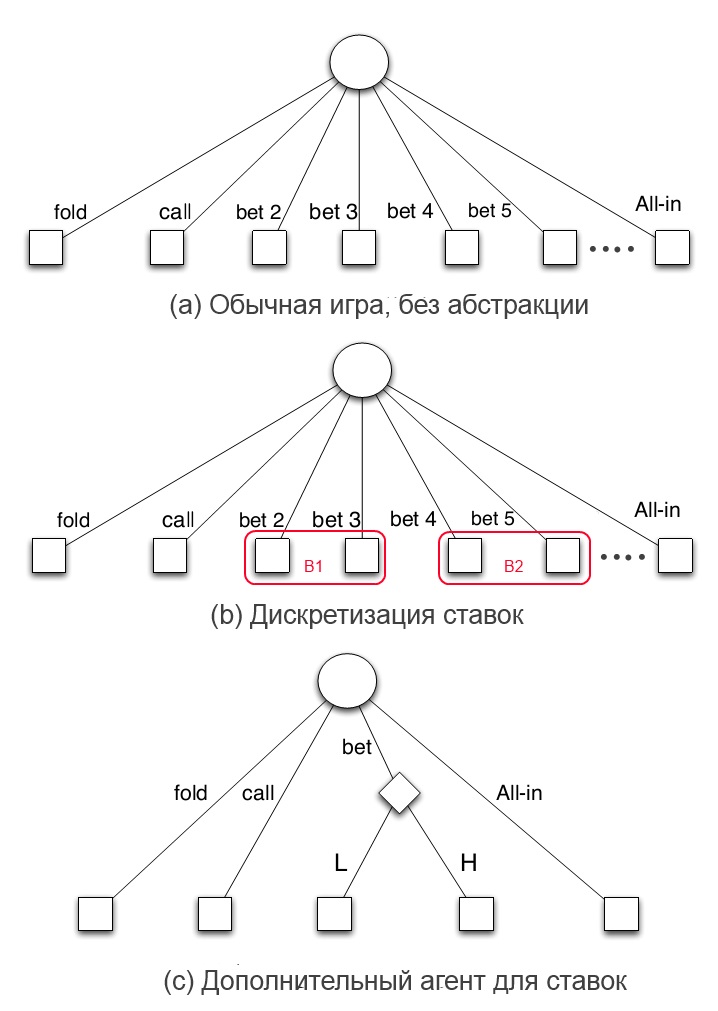
Различные способы представления ставок в безлимитном покере.
Иногда встречаются абстракции, в которых ограничено количество ставок на кругах торговли или же полностью отсутствует история о предыдущих кругах. Но на сегодняшний день такие подходы особой популярностью не пользуются, так как они порождают слабых покерных агентов.
Комбинации карт в абстракциях
Самое сложное и самое важное при построении абстракции для покера — представление карточных комбинаций. Именно это определяет то, насколько адекватно бот будет воспринимать текущую игровую ситуацию и принимать стратегически верные решения.
Ниже представлена таблица из отчета [1], в которой перечислены размеры множеств всевозможных комбинаций карт в Техасском Холдеме на каждом кругу торговли. В первой колонке представлены варианты раздач карманных карт обеим игрокам в сочетании с общими картами на доске. Во второй колонке содержится та же информация, но для одного игрока, т.е. для сочетаний одной пары карманных карт и общих карт. И, наконец, последний столбец содержит в себе количество неэквивалентных классов карточных комбинаций для одного игрока. Напомним, что эквивалентными комбинациями называются такие наборы карточных комбинаций, в которых заменой мастей можно получить любую другую комбинацию из этого же набора. Совершенно очевидно, что эквивалентные комбинации содержат в себе одну и ту же стратегическую информацию.
| Круг торговли | Всего для двух игроков | Всего для одного игрока | Неэквивалентные для одного игрока |
| Префлоп | 1,624,350 | 1,326 | 169 |
| Флоп | 28,094,757,600 | 25,989,600 | 1,286,792 |
| Терн | 1,264,264,092,000 | 1,221,511,200 | 55,190,538 |
| Ривер | 55,627,620,048,000 | 56,189,515,200 | 2,428,287,420 |
В качестве примера эквивалентного класса можно привести комбинацию AKx|TxJy82x на третьем кругу торговли, где AKx — карманные карты игрока, TxJy82x — карты на доске в порядке их появления, а x и y (x!=y, разумеется) могут принимать одно из четырех значений мастей {c,s,h,d}. Таким образом, класс AKx|TxJy82x содержит в себе 12 абсолютно одинаковых комбинаций {AKc|TcJs82c, AKs|TsJc82s, ...}. Условимся называть комбинацию, записанную в виде AKx|TxJy82x, рукой игрока, хотя это и идет несколько в разрез с общепринятым определением. Тем не менее, термин рука как нельзя точно подходит к определению частной информации о картах, полностью доступную только одному игроку.
Даже после приведения рук к эквивалентным классам их слишком много для непосредственного рассмотрения, поэтому необходимо прибегнуть к группировке этих эквивалентных классов в новые, абстрактные классы. Разумеется, теперь эта процедура будет происходить с некоторой потерей информации об исходных эквивалентных классах.
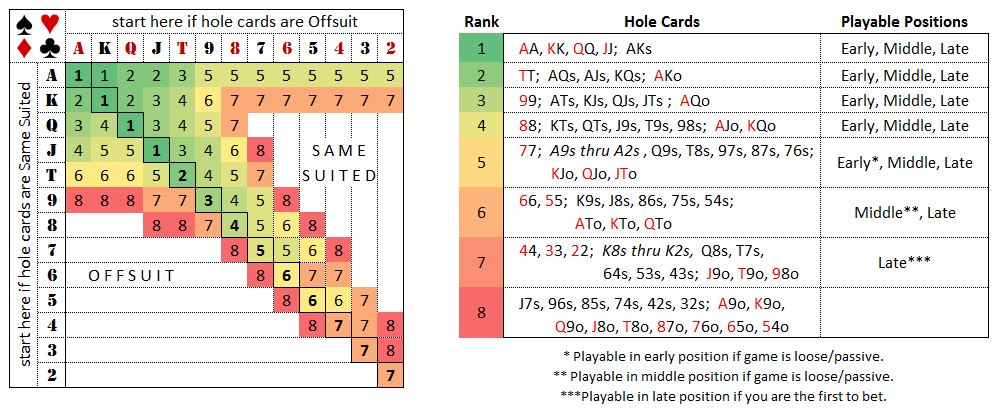
Для примера такой группировки рук, рассмотрим префлоп, поскольку на нем всего 169 неэквивалентных карманных пар. Многие из заинтересованных читателей знакомы с именем известного теоретика и игрока в покер Дэвидом Склански, одним из достижений которого является детально проработанная стратегия игры на префлопе. На рисунке ниже показана группировка стартовых рук по их стратегической ценности, предлагаемая Склански [6]. Это разбиение на восемь классов не является единственно верным, но дает хорошее представление о принципах построения карточных абстракций в покере.
К сожалению, уже начиная с флопа ручной анализ карточных комбинаций является весьма утомительным и неблагодарным делом, поэтому приходится прибегать к другим способам анализа и разбиения рук на классы. Речь пойдет о числовых характеристиках карточных комбинаций, которые позволяют осуществить группировку карточных комбинаций по выделенным свойствам.
Одной из самых первых использованных характеристик стал ранг руки (Hand Strength, HS), который определяется как доля всех возможных готовых комбинаций у оппонента, уступающих по силе готовой комбинации у игрока. Например, HS(AKx|TxJy82x)=1.0 так как имеется уже готовый старший флеш, а вот HS(AxKy|TzJx82z)~0.43, что неудивительно, так как любая пара карт с мастью z у оппонента дает ему преимущество.
Первое, что бросается в глаза при анализе HS, это то, что этот показатель ничего не говорит о том, как поведет себя рука игрока на последующих кругах торговли, не говоря уже о том, что и предыстория раздачи никак не отражается на значении этого показателя. С целью восполнить недостающую информацию, начиная с флопа, вводятся еще два показателя PPot (Positive Potential) и NPot (Negative Potential). Первый из этих показателей PPot представляет собой вероятность того, что текущая рука игрока улучшится после появления новой карты на столе. Под улучшением подразумевается, что у оппонента не появится новых готовых комбинаций, которые окажутся старше готовой комбинации игрока. Аналогично и Npot — вероятность того, что рука игрока ухудшится с новой картой на столе. Подробное описание этих показателей и процедур их расчета можно найти в [7-8]. Для рассмотренного выше примера PPot(AKx|TxJy82x)=0 и NPot(AKx|TxJy82x)~0, что неудивительно, так как оппоненту приходится рассчитывать только на фулл-хаус при наличии у него готовых двух пар. Для второго случая PPot(AxKy|TzJx82z)~0.15 и NPot(AxKy|TzJx82z)~0.22 и мы видим, что NPot достаточно высок за счет того, что оппонент может добрать недостающую карту с мастью х, чтобы собрать флэш.
В работе [9] приводятся сведения о том, что квадрат ожидаемого ранга руки E[HS2] позволяет получить более качественную абстракцию, поскольку такой показатель дает больше преимуществ сильным рукам игрока и разграничивает их с руками, у которых высокий потенциал (PPot). Логично, ведь руки с одинаковым рангом, но с разным потенциалом, должны стратегически по разному разыгрываться.
Три показателя {HS, PPot, NPot} позволяют точнее охарактеризовать руку игрока, но их одновременное рассмотрение может оказаться несколько неудобным делом, поэтом часто прибегают к вычислению эффективного ранга руки (effective hand strength, EHS), который задается по одной из двух формул [7-8]: EHS1= HS×(1−NPot)+(1−HS)×PPot, или, EHS2= HS+(1−HS)×PPot. Разница между двумя формулами заключается в том, что EHS2 дает более «оптимистичный» прогноз, что бывает необходимо для проработки более агрессивной игры.
Еще один показатель, о котором многие уже догадались, это шанс выигрыша руки или ожидаемый ранг руки на вскрытии (expected hand strength, E[HS]). Как ясно из названия этой характеристики, она представляет собой долю случаев, когда доиграв до вскрытия текущий игрок получит комбинацию старше возможной комбинации оппонента. Плюс этого показателя заключен в том, что он уже включает в себя информацию о динамике руки на всех последующих кругах торговли вплоть до вскрытия, в отличие от NPot и PPot, прогнозирующих лишь на одну улицу вперед. В примерах выше, против случайной руки оппонента эти показатели имеют следующие значения: E[HS](AKx|TxJy82x)~0.99 и E[HS](AxKy|TzJx82z)~0.42.
У всех вышеописанных показателей есть ряд общих недостатков. Первый из них, самый заметный для опытных игроков в покер, заключен в том, что эти показатели рассчитываются при предположении наличия любой руки у оппонента. Смысл в том, что в покере очень малый процент рук доходит до вскрытия, что означает, что при расчете HS, PPot, NPot или E[HS] мы ставим оппоненту все возможные карманные карты, которых у него может никогда и не быть. Это в свою очередь делает оценки таких показателей непредсказуемо завышенными. Чтобы как-то исправить этот недостаток, часто применяют взвешивание рук, возможных у оппонента в зависимости от игровой ситуации. В частности, такое взвешивание может быть осуществлено с помощью моделирования оппонента.
Второй недостаток кроется в том, что применение этих показателей все же приводит к потере информации о руке игрока, хотя это не так очевидно. В первую очередь это касается «памяти» руки, а именно информации о том, в какой последовательности карты появлялись на доске. Например, очевидно, что HS(AKx|QJT5x)=HS(AKx|JT5Qx), где в первом случае у игрока на флопе уже была готовая комбинация стрит-флеша, а во втором — нет. Более того, зачастую руки, требующие разных стратегических решений, имеют близкие между собой значения числовых показателей, что может привести (и приводит) к ошибкам при обучению машины игре в покер.
Дальнейшие манипуляции с числовыми показателями с целью построения абстракции, сводятся к группировке различных категорий рук в классы по определенным значениям этих показателей. Например, если мы желаем иметь всего пять классов на каждом кругу торговли, то мы можем сгруппировать все руки по следующим значениям E[HS]:
[0.0–0.2] [0.2–0.4] [0.4–0.6] [0.6–0.8] [0.8–1.0].
Теперь абстрактная игра в покер будет манипулировать пятью классами рук, а не исходными карточными комбинациями. Для того, чтобы такая абстрактная игра была полной, необходимо также рассчитать вероятности перехода между классами на смене кругов торговли и задать матрицу выплат, в которых указана «прибыльность» одного абстрактного класса рук по отношению к другому.
Абстракция с помощью группировки рук по классам может быть выполнена как вручную, так и с помощью автоматизированных процедур, например, с помощью методов кластеризации данных. Ручное создание абстракций позволяет в какой то мере обеспечить понимание решений бота, облегчить отладку и корректировку стратегии, но является весьма трудоемким процессом. Автоматические методы группировки зачастую руководствуются критериями, которые не всегда подходят под задачи в покере. С другой стороны, автоматический подход позволяет легко и быстро манипулировать параметрами абстракций, что позволяет быстро и оптимально подобрать подходящую конфигурацию.
Рассмотренный выше пример разбиения рук по классам с помощью пяти предопределенных интервалов значений E[HS] имеет один недостаток — руки по классам распределяются неравномерно — в какой то диапазон значений E[HS] попадет всего пара рук, а в остальных будет перенаселение. Чтобы исправить эту ситуацию, используют разные приемы, от ручного редактирования классов, вычисления квантилей, разбиения на вложенные классы, k-means и другие.
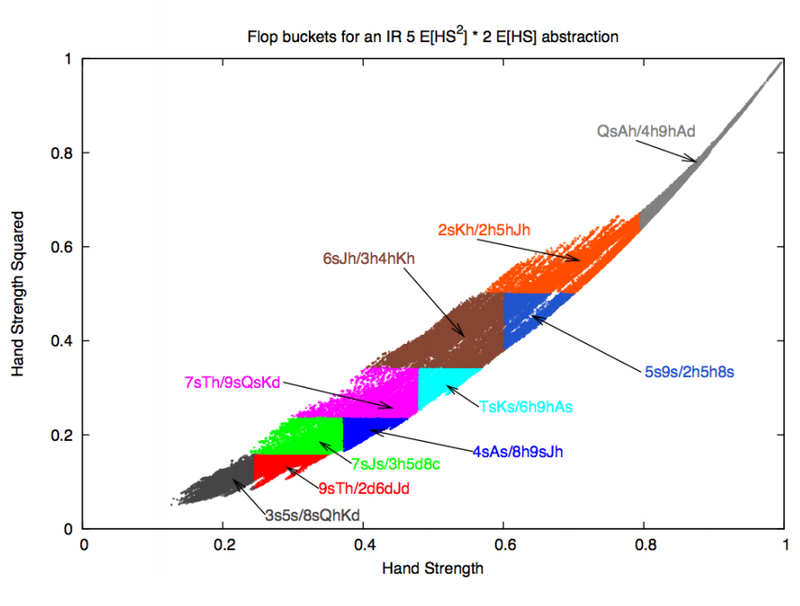
Пример группировки рук с помощью показателей E[HS2] и E[HS] на флопе с разбиением на вложенные классы.
Заключение
По моему скромному мнению, современный компьютерный покер это игра абстракций, в которой побеждает тот агент, чья абстракция оказалась качественнее, точнее и, что немаловажно, меньше. Размер абстракции упомянут не зря, ведь именно от него зависит время затраченное на обучение агента игре. И будут ли это тысячелетия, годы или пара часов — зависит от исследователя, проектирующего структуру абстракции. К сожалению, данная публикация никак не может претендовать на полный обзор различных подходов к построению абстракций, поскольку их существует очень много. Тем не менее, я думаю, что основные моменты в этой области отражены и цель заинтересовать читателя проблемами компьютерного покера достигнута.
[1] M.B. Johanson, «Measuring the Size of Large No-Limit Poker Games»
[2] A. Gilpin et al., «A Heads-up No-limit Texas Hold’em Poker Player: Discretized Betting Models and Automatically Generated Equilibrium-finding Programs»
[3] Презентация CMPUT 495 Honors Seminar
[4] J. Hawkin et al., «Automated Action Abstraction of Imperfect Information Extensive-Form Games»
[5] J. Hawkin et al., «Using Sliding Windows to Generate Action Abstractions in Extensive-Form Games»
[6] Texas hold 'em starting hands
[7] A. Davidson, Opponent Modeling in Poker: Learning and Acting in a Hostile Environment (postscript)
[8] D. Billings et al., «The challenge of poker»
[9] M.B. Johanson, «Robust Strategies and Counter-Strategies: Building a Champion Level Computer Poker Player»
Не менее интересные материалы, в тексте не упоминаемые
A. Gilpin and T. Sandholm, «Lossless abstraction of imperfect information games»
A. Gilpin and T. Sandholm, Better Automated Abstraction Techniques for Imperfect Information Games, with Application to Texas Hold’em Poker
Обзор покерных калькуляторов для различных языков программирования
Автор: kenoma