
Покер давно привлекает исследователей самых различных мастей от любителей до серьезных ученых. И, не секрет, что столь пристальное внимание к покеру коррелирует с ростом популярности онлайн гэмблинга, который бурно развивался в 00-х годах. На сегодняшний день человек уже уступил лимитный хедс-ап Техасский Холдем машине, в то время как в безлимитных и многоместных покерных дисциплинах человек все еще берет верх. Наибольший вклад в проблему построения сильного компьютерного покерного интеллекта, вне всякого сомнения, внесла исследовательская группа из университета Альберты, а предложенное ими семейство алгоритмов поиска равновесных стратегий является на сегодняшний день самым модным и часто используемым средством при построении покерных агентов. Но обо всем по порядку.
Данная публикация затрагивает исключительно проблемы искусственного интеллекта в покере, вопросы, касающиеся получения информации из клиентов онлайновых казино, обхода безопасности и имитации пользовательских действий рассмотрены не будут. Предполагается, что читатель уже знаком с правилами покера.
О сложности покера для машинного обучения
Покер примечателен тем, что он является игрой с неполной информацией — ваш противник не знает ваших карт. Также в нем присутствуют элементы случайности — карты игроков и на доске выметаются из колоды случайным образом. К этим двум аспектам игры в покер добавляется еще и третий — количество игровых состояний, которое в некоторых покерных дисциплинах лишь слегка уступает шахматам. Чтобы представить себе масштаб проблемы, стоящей перед исследователем, рассмотрим лимитный хэдс-ап вариант Техасского Холдема. На рисунке ниже схематически показана структура такой игры с указанием новой информации, появляющейся на каждом раунде торговли.
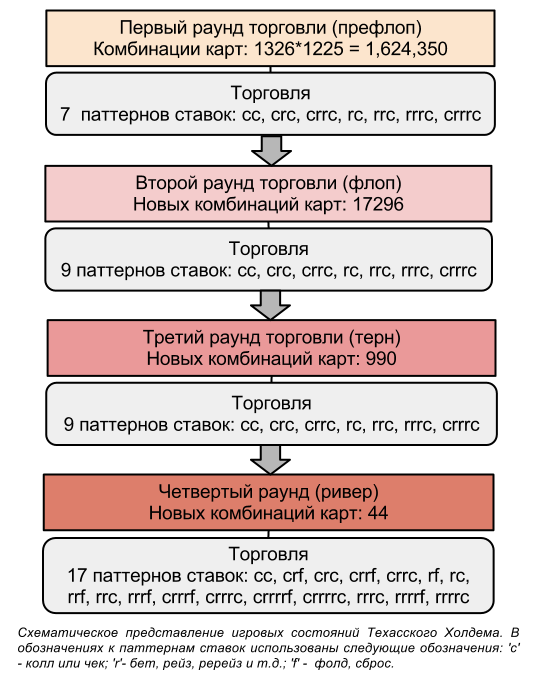
В рассматриваемом нами варианте покера порядка 1018 игровых ситуаций, что делает эту задачу, мягко говоря, не решаемой в лоб, поскольку требует совершенно немыслимых вычислительных ресурсов. Однако следует заметить, что некоторые карточные комбинации эквивалентны между собой, так, например, на префлопе стартовая комбинация из двух тузов A♥A♦ абсолютно идентична любой другой паре тузов. Таким образом, рассматривая первый круг торговли, на котором у игроков всего по две карты на руках, мы можем выделить всего 169 различных неэквивалентных двухкарточных комбинации. Но даже после выделения эквивалентных классов карточных комбинаций Техасский Холдем имеет порядка 1014 различных игровых состояний, требующих для своего хранения десятки петабайт памяти, не говоря уже о времени, которое будет затрачено на то, чтобы все это обучить игре в покер. Стоит ли после этого заикаться про вариации покера для 3-х и более игроков?
Обычным делом в случаях, когда исходная игра слишком велика для непосредственного изучения, является переход к абстрактной игре (абстракции), объединяющей в своих игровых состояниях близкие в стратегическом смысле состояния полной игры. Другими словами, при анализе и решении игры некоторые состояния исходной игры трактуются как неразличимые. В качестве примера построения абстракции в покере, рассмотрим префлоп, где, как известно, лучшими стартовыми комбинациями являются пара тузов AA и одномастные сочетания туза с королем AKs. Совершенно очевидно, что стратегии розыгрыша этих карт на первом кругу торговли несильно будут отличаться друг от друга, поэтому можно без зазрения совести объединить эти две пары карт в один абстрактный класс стартовых комбинаций. Указанный трюк можно повторить и для других карточных комбинаций, получив в итоге, как вы уже догадались, «абстрактный» покер с меньшими запросами к вычислительным ресурсам.
Существуют и другие способы построения абстракций, которые применяются не только к карточным комбинациям, но и к паттернам ставок в безлимитных дисциплинах, что позволяет в итоге получить абстрактную игру, поддающуюся исследованию и анализу. Ключевым моментом здесь является то, что при переходе к абстракции теряется часть информации об исходной игре. Чем существеннее утраченная информация, тем более уязвимым станет в итоге покерный агент.
Рассмотрим теперь основные концепции построения стратегических профилей для игры в покер.
Экспертные системы
Самые первые покерные агенты являлись экспертными системами или наборами правил if-then для различных игровых ситуаций. Такие правила вбивались ручками с помощью самих игроков и/или получались с помощью анализа большого количества реальных игровых раздач. Как бы то ни было, недостаток такого подхода очевиден — искусственный оппонент легко эксплуатируется после выявления слабых мест. Разумеется, эти слабые места всегда можно подкорректировать добавлением новых записей в базу правил, но это влечет за собой ряд неприятностей, связанных с растущей сложностью поддержки, отладки и снижающейся производительностью системы в целом.
На сегодняшний день покерные агенты данного типа в чистом виде практически не используются ввиду их легкой эксплуатируемости. Наиболее известные представители этого класса ботов: первые версии Loki и Poki, FellOmen и широко известный в узких кругах Shanky Bot.
Эксплуататоры
Основная концепция покерных ботов-эксплуататоров основана на построении контр-агентов к известным оппонентам, использующих их слабые места для получения максимальной прибыли от игры. Как правило, используются либо моделирование поведения оппонента в той или иной игровой ситуации, либо заранее посчитанные стратегические профили под определенного оппонента.
Принятие решения в системах с моделированием оппонента сводится к многократному проигрыванию «виртуальных» раздач с различными исходами для определения наиболее выгодного решения. Адекватность таких покерных агентов обусловлена адекватностью модели оппонента. Но, когда речь заходит о моделировании решений человека, всегда невольно вспоминается гадалка Шеннона, которая угадывает действие игрока в девяти случаях из десяти. Чаще всего для моделирования живых оппонентов используются нейросети, которые, как сообщают некоторые источники, могут давать ~80-90% надежность предсказания действий игрока. Это обстоятельство делает данный вид покерных ботов наиболее привлекательным для игры в онлайн казино, так как современные GPU-технологии позволяют легко и быстро построить модель оппонента и вычислить выгодное решение.
В академических кругах известны эксплуататоры основанные на нахождении стратегий наилучшего отклика. Идея данного подхода заключена в том, что в рамках заданной абстракции подбирается контр-стратегия к известному оппоненту. Это позволяет эксплуатировать слабости конкретного оппонента максимально эффективно, но против произвольного соперника результаты могут оказаться плачевными. Более того, построение таких стратегических профилей требует значительных вычислительных ресурсов, хотя в последнее время появились подвижки и в этой области.
Для любого бота-эксплуататора существует один недостаток. Он заключен в необходимости реализации начальной стратегии, так как очевидно, что невозможно смоделировать и эксплуатировать оппонента после десятка раздач. Более того, речь идет о десятках тысяч раздач с конкретным противником, прежде чем эксплуатация начнет приносить свои плоды. Обычно, во время набора статистики на оппонента используются покерные боты другого типа. При игре с людьми на начальном этапе очень часто используется подход, при котором эксплуататор заранее обучается по истории раздач против группы игроков, объединенных общими характеристиками, такими как частота захода в игру, желание идти на вскрытие и так далее. Затем, по мере наигрывания игровых раздач, характеристики человека-оппонента проясняются все сильнее и сильнее, что позволяет эксплуататору быстрее и адекватнее подобрать и дообучить соответствующую контр-стратегию.
Качество игры эксплуататоров намного превосходит экспертные системы, так как они способны выявить слабые места последних. Их эффективность против произвольных оппонентов во многом определяется тремя факторами — начальной стратегией, набранной статистике на оппонента и адекватности используемой модели. Самыми известными ботами этого класса являются BRPlayer и Vexbot, знакомый многим по Poker Academy.
Равновесные стратегии
До относительно недавнего времени чистые теоретико-игровые методы построения покерных ботов относились больше к области академического интереса, поскольку их осуществление было сопряжено с вычислительными сложностями. Речь прежде всего идет о поиске равновесий Нэша.
Остановимся подробнее на концепции равновесных стратегий и рассмотрим всем известную игру Камень-Ножницы-Бумага, разыгрываемую достаточно большое количество раз. Пусть первый игрок следуя чистой стратегии играет все время камень. Тогда второй игрок, раскусивший игру первого, для получения максимального профита будет играть все время бумагу. Первому игроку, чтобы не проигрывать да еще и максимизировать свои выигрыш, нужно переключиться на ножницы. Очевидно, что второй игрок изменит свою стратегию на камень и весь цикл смены стратегий повторится вновь. Как легко заметить, если бы первый игрок выкидывал камень, ножницы или бумагу равновероятно, то второй игрок, как бы ни старался изменить свою стратегию, не смог бы эксплуатировать противника.
Вышеописанный пример можно рассматривать как игру двух эксплуататоров, постоянно подгоняющих свою смешанную стратегию под оппонента. Очевидно, что рано или поздно стратегии обоих игроков сойдутся к равновероятному выкидыванию камня, ножницы или бумаги. Такая особая ситуация получила названия равновесия Нэша, поскольку находясь в равновесии ни один из игроков не может сыграть лучше другого, изменив свою стратегию.
Как уже упоминалось выше, нечего и думать о поиске равновесных стратегий для покера — еще нескоро человечество будет располагать ресурсами достаточным для решения игр такого размера. Поэтому исследователи сосредоточились на равновесных стратегиях абстракций покера, но тут возникает вопрос, связанный с тем, насколько адекватно равновесие абстрактной игры соответствует равновесию полной игры. В связи с этим равновесия Нэша абстрактной игры принято называть приближенными равновесиями или ε-равновесиями, где ε символизирует потенциальную эксплуатируемость стратегии.
У ε-равновесий главной характеристикой выступает их эффективность при игре с супер-эксплуататором. Или, другими словами, насколько далеко от истинного равновесия исходной игры располагается найденное ε-равновесие. Вполне ожидаемо, что использование слишком грубых или неадекватных абстракций дает грубое и неадекватное ε-равновесие. Также вполне ожидаемо, что чем меньше информации о полной игре теряется при переходе к абстракции, тем больше сама абстракция и выше требования к алгоритмам обучения и вычислительным ресурсам. Это в свою очередь повлекло поиск и разработку новых методов поиска равновесных систем для таких больших игр.
На сегодняшний существует несколько эффективных алгоритмов поиска равновесия в больших абстракциях покера. Самыми популярными из них являются алгоритмы, основанные на минимизации сожаления. Это семейство алгоритмов активно разрабатывается исследовательской группой университета Альберты и заслуживает отдельного рассмотрения. Отмечу лишь, что с помощью одного из таких алгоритмов был обучен покерный бот Slumbot, в котором первые три круга торговли представлены безо всякой абстракции. Этот бот занял первое место в прошлом году на Annual Computer Poker Competition.
Главным преимуществом равновесных стратегий является их неэксплуатируемость. В то же время, эти стратегии не особо прибыльны даже против очень слабых игроков в покер. Наиболее известными представителями этого класса покерных агентов, использующих равновесные профили стратегий, являются Hyperborean и Polaris, первый бот, который уверено сумел обыграть человека в покер.
Вместо заключения
Данный мини-обзор отнюдь не претендует на полноту изложения проблем компьютерного покера, но может дать приблизительное представление о положении дел в этой области на сегодняшний день. Возможно, если дело хорошо пойдет, то могу продолжить раскрывать эту тему.
Автор: kenoma

