
В ноябре 2012 года Рэндал Монро опубликовал комикс xkcd с календарём, в котором размер чисел каждого месяца был пропорционален тому, как часто это число упоминается в книгах по своему имени (например, «14 октября») в базе данных Google Ngrams с 2000 года. Большинство крупных дат довольно очевидны: 4 июля, 25 декабря, первое число каждого месяца, последнее число почти всех месяцев, ну и 11 сентября, оставляющее всех позади. Не так уж много дней выглядит сильно меньше остальных. К примеру, 29 февраля – крохотная точка. Но если приглядеться, можно увидеть, что 11 число каждого месяца относительно маленькое. К комиксу шло примечание: «Во всех остальных, кроме сентября, месяцах, 11-е упоминается гораздо реже остальных дат. Так было и до 11 сентября, и я не знаю, почему это так». Я покопался в данных, и думаю, что разобрался, почему.
Сначала я убедился, что 11-е отличается от остальных. В месяце может быть до 31 дня, и какие-то из этих дней обязательно будут наименьшими из всех. Может быть, 11-е число на календаре не самое мелкое, просто наш глаз за это цепляется. Так что я сравнил реальные данные, а не просто изучил комикс. База данных Ngrams возвращает общее количество раз, которое фраза упоминается за год, нормализованное по количеству вышедших в тот год книг.
Я выбрал количество каждого из дней года (1 января, 2 января) и построил медианы по месяцам для каждого из дней месяца (1 января, 1 февраля и т.п.) для каждого года. Это показало, как часто 11-е и 30 других дней упоминаются в выбранном году. Медиана позволяет сгладить всплески от дней типа 4 июля. Медиана будет выглядеть необычно, только если порядковый номер будет сильно отличаться в не менее чем 6 из 12 месяцев.
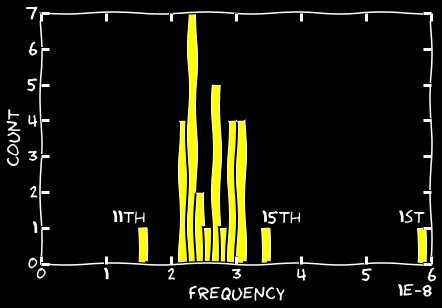
Я построил медианы для каждого порядкового номера с 2000 по 2008 года. Ниже приведена гистограмма для 31 медианы. Первое число выделяется из всех, а 15 едва видно среди оставшихся. Но результат у 11-го числа меньше всех на довольно большую величину (с Р-значением < 0,05), что на первый взгляд сложно объяснить.
И этот недостаток существует уже давно. На следующем графике – все порядковые номера для каждого из готов промежутка 1800-2008. Данные сглажены по 11 годам, чтобы убрать шум. Даже в самом начале 11-е гораздо ниже основной группы. Его небольшой недостаток сохраняется несколько десятилетий, а затем в 1860-х 11-е внезапно отклоняется от своей позиции последнего в ряду средних. Разрыв между 11-м и обычными порядковыми номерами резко увеличивается, и в результате значение для частоты его упоминаний становится примерно вполовину ниже, что продолжается в первой половине XX-го века. Во второй половине разрыв сокращается, но не исчезает до самого конца.
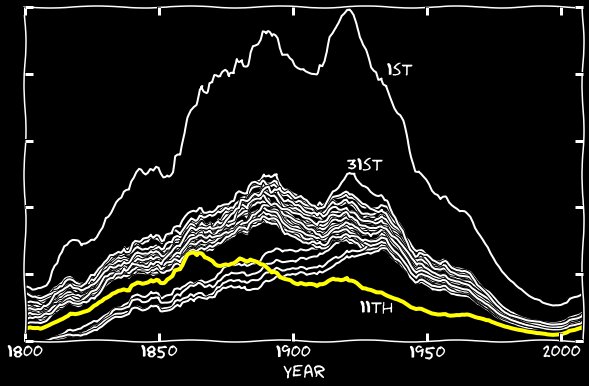
Внимательные читатели заметят ещё одну странность. Есть ещё 4 линии, находящиеся ниже, чем они должны быть. Сверху вниз это 2-е, 3-е, 22-е и 23-е числа. С 1800 по 1890-е они находятся даже ниже, чем 11-е. Но с 1900-го их разрыв сокращается, в то время как разрыв с 11-м начинает увеличиваться, и полностью исчезает к 1930-м. Это тоже довольно интересная тема, которую мы рассмотрим чуть позже.
Типографские курьёзы
Начиная исследование, я надеялся найти тайное табу на события 11-го числа или типографическое отклонение от правил печати. Увы, причина оказалась гораздо более приземлённой: число 1 очень похоже на прописную I (i) или на строчную l (L) в большинстве шрифтов, используемых при печати книг. А также 11 можно перепутать с n. Алгоритмы от Google ошибаются, распознавая 11 на странице, и интерпретируют порядковый номер как некое слово.
Мы можем напрямую поискать бессмысленные фразы типа ll марта или II июля или ii мая. 11 можно спутать с девятью комбинациями из I, l и i. Пять из них действительно встречаются в базе данных, хотя бы для одного месяца: II-ный, Il-ный, ii-ный, li-ный и ll-ный. Также нашлись варианты с только одним неправильным символом, 1l-ный, 1i-ный и l1-ный. Я назвал эти ошибки xxth. Google Books делает запросы к более новой базе данных, чем Ngrams, но примеры таких ошибок всё равно можно отыскать. Вот, например, гугль распознаёт следующее, как II января:

Как ll февраля:

А вот li марта:
Таких примеров в базе полно. Можно найти и другие ошибочно интерпретированные порядковые номера, но 11-е встречается гораздо чаще других.
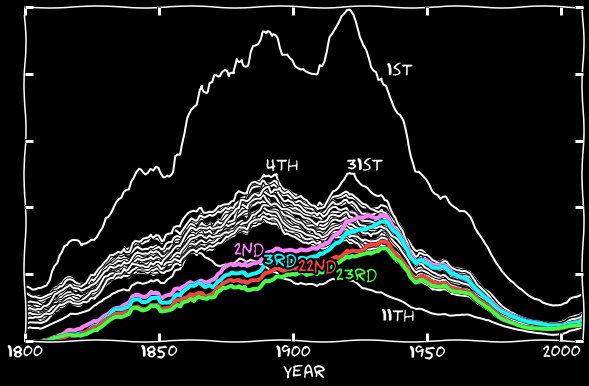
Я добавил в свои подсчёты II января, ll января, и т.д., и сделал то же для других месяцев. Следующий график показывает, что 11-е получает большой прирост от такого добавления. До 1860-х разница между 11-ми и основной группой исчезла. После 1860-х исчезла треть или четверть этой разницы.
А куда делись остальные 11-е? С 1860-х гугловский алгоритм начинает странным образом ошибаться – вместо 11-х он распознаёт n-ные. Вот пример страницы, заполненной n-ными числами января:
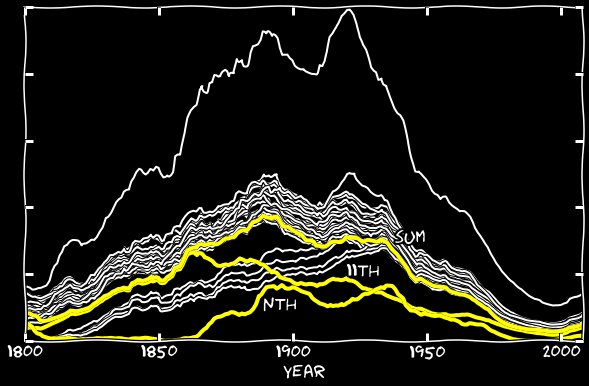
В некоторых годах количество неправильных распознаваний превышает количество правильных. Я добавил n-ное число января к 11-м января, и сделал то же с другими месяцами. На следующем графике показаны как n-ные числа, так и их сумма с 11-ми. До 1860-х их вклад был незначителен, но потом эта ошибка начинает отвечать почти за все пропавшие 11-е.
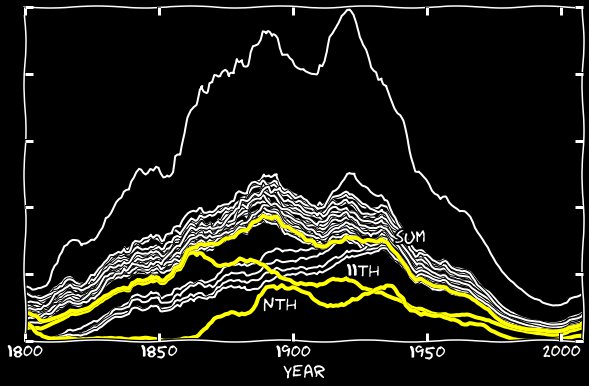
Комбинированный график
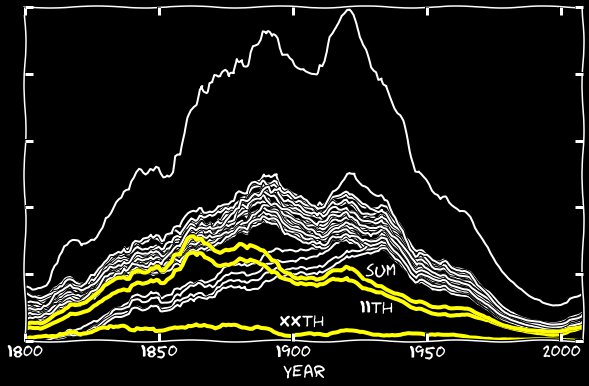
Добавив xxth и n-ные ошибки в график 11-х, я устранил разрыв по всей длине графика, и 11-е стало выглядеть так же, как все остальные даты. Выходит, что неправильное распознавание 11-го в виде n-ного, II, ll, и так далее, ответственно за малое количество 11-х чисел среди других дней месяца.
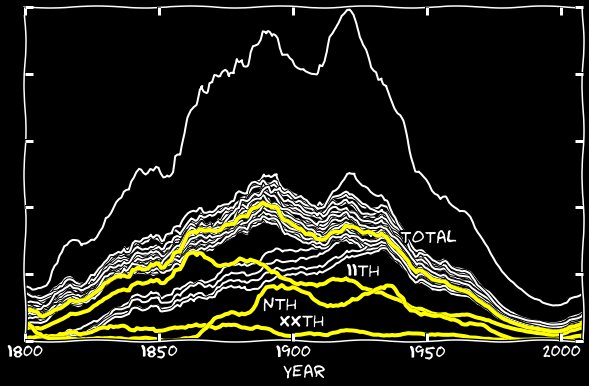
Типографические машины
Хотя понятно, почему 11-е было чаще других распознано неправильно, почему количество ошибок столь неравномерно? Что случилось в 1860-х, из-за чего так сильно подскочил процент ошибок? Я подозреваю, что это связано с изобретением в 1860-х такого устройства, как пишущая машинка. У самых ранних пишущих машинок не было отдельной клавиши для номера 1. Предлагалось вместо него использовать букву l (L) в нижнем регистре. И когда алгоритм распознаёт ll-ное октября, он на самом деле делает это правильнее, чем мы считали. В Google books не так много напечатанных на машинке документов, но это популярное устройство сильно повлияло на развитие шрифтов. 1 и l не отличались на всё больше распространявшихся машинках, и даже типографский шрифт стал оправдывать ожидания этого сходства. Сравните эти символы в шрифте 1850 года:
Видна разница между l без засечки вверху и 1 с явной засечкой. Сравните их в шрифте 1920 года:
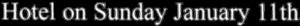
Символы идентичны, за исключением кернинга. И сегодня большинство шрифтов изображают 1 и l в виде высоких символов с двумя засечками внизу и одной, направленной влево, вверху. Только угол у засечки 1 чуть больше, чем у l. Качество печати книг с 1970 года способствует уменьшению количества неправильных распознаваний, но полностью они не исчезли, поэтому оставшиеся проблемы и проявились на комиксе от xkcd.
Открытым остаётся вопрос популярности ошибки, при которой 11 заменяется на n-ное. Это довольно странная ошибка. n-ный часто встречается в математике и научных публикациях, и это может повлиять на его популярность. В большинстве шрифтов верхняя часть n очень тонкая, и наверно может быть не видна в текстах, на которых тренировался алгоритм. Но в росте 1 и n есть большая разница, особенно в эпоху пишущих машинок, где происходит много ошибок. Но фраза n-ное января – это нонсенс, поэтому шансы такого распознавания должны были уменьшиться. Возможно, в каких-то современных текстах содержались ошибки, и в них 11-е были промаркированы, как n-ные, что и послужило источником ошибок? Единственный способ это узнать – открыть исходный код алгоритма от Google, распознающего текст. Это упражнение мы оставим читателю.
Пропажа 2, 3, 22 и 23-х
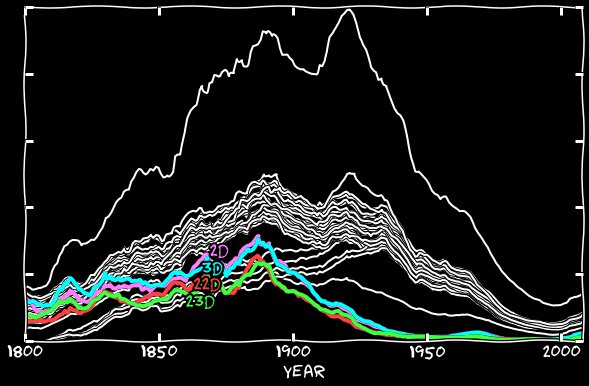
С 11-ми числами мы разобрались, но во время исследования их поведения я столкнулся с ещё одной загадкой – непонятно низкое количество 2-х, 3-х, 22-х и 23-х чисел, но только до 1930-х годов, после чего их количество выравнивается.
На графике ниже расположены все числа, и по нему выходит, что в 1800-х годах указанные даты вообще не используются. Первые упоминания о наших датах появляются в 1810-х, их количество растёт с той же скоростью, что и у остальных дат, но сохраняет при этом разрыв с ними – их число примерно в два раза меньше. Внезапно в 1890-х разрыв уменьшается, и так происходит до 1930-х, когда они, наконец, вливаются в основную группу.
Дореволюціоннымъ стилемъ
Так что же, числа 2 и 3 в XIX-м веке были несчастливыми? Алгоритм от Google с трудом распознавал двойки и тройки в старых шрифтах? Нет, оказывается, что раньше вместо теперешней английской записи «2nd, 3rd, 22nd, 23rd» было принято писать «2d, 3d, 22d, 23d». Я построил медиану для January 2d, February 2d и других месяцев, и так же поступил с оставшимися датами. На графике ниже показана частота появления этих дат в старом стиле записи – они начинают с частотой других дат, но потом постепенно исчезают к 1890-м, и полностью растворяются к 1930-м.
Иногда можно встретить современное использование старой формы записи, если оно используется в названии с долгой историей, типа 3d Marine Division. Но остаточное использование такой записи происходит в основном из-за существования репринтов старых книг и публикаций старых дневников.
Комбинированный график
Если добавить старый стиль к новому, мы получим следующий график. Из него следует, что правильно подсчитанные даты почти ничем не отличаются от всех остальных.
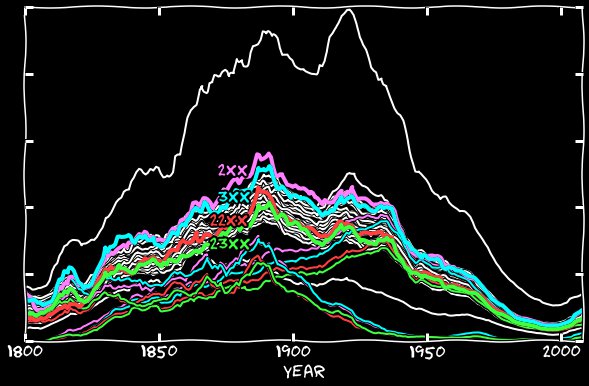
Почему теперь получается, что упоминания 2-х и 3-х чисел иногда превышают по частоте остальные, остаётся для меня непонятным. Думаю, что по причине слишком частого упоминания 1-го числа месяца, 2-е и 3-и числа тоже должны упоминаться чуть чаще. Но если поискать в Google Books вхождения January 2d или January 2nd, можно найти довольно много подобных пассажей:
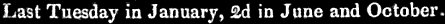
Видимо, Google Books игнорирует запятые. Так что, хотя числа месяца с 1 по 4 ничего особенного собой не представляют, такие вот примеры могут влиять на статистику.
Рассуждения
Почему раньше писатели использовали такие однобуквенные аббревиатуры? Возможно, из-за латыни, где индикатором порядкового номера служила буква о. В таких романских языках, как испанский, итальянский и португальский, до сих пор используются о или а. Мы бы до сих пор использовали d, если бы не 1st, 4th и т.п., у которых последняя согласная не выражается в английском одной буквой. Получилось, что следование английскому языку перевесило желание подражать латыни.
Автор: SLY_G





