Постановка задачи
В предыдущих статьях «Основы подхода к построению универсального интеллекта», часть 1 ( http://habrahabr.ru/post/145309/ ) и часть 2 ( http://habrahabr.ru/post/145467/ ), мы в общих чертах описали разные существующие подходы и сформулировали некоторые методологические принципы, которые целесообразно выполнять при разработке универсального ИИ. В статье «Идеальный ученик, или о чем умалчивается в машинном обучении» ( http://habrahabr.ru/post/148002/ ) необходимость соблюдения этих принципов (и, в особенности, сохранение универсальности) было обсуждено на примере проблемы машинного обучения. Здесь мы разберем одну распространенную модель универсального интеллекта в целом. Хотя эта модель крайне далека от реального универсального ИИ, она позволяет понять критические недостатки других подходов.
Попробуем рассмотреть модель идеального минимального интеллекта (ИМИ) как рационального агента, пытающегося, действуя в некотором мире, максимизировать свою целевую функцию (функцию полезности). Здесь мы будем полностью пренебрегать требуемыми вычислительными ресурсами, и попробуем посмотреть, можно ли построить универсальный ИИ хотя бы в таких условиях. Практически не умаляя общности можно считать, что агенту в дискретные моменты времени доступен конечный набор элементарных действий и показаний сенсоров. Набор сенсоров включает как внешние, так и внутренние, в том числе, и целевую функцию. Практически любую, как частную, так и общую задачу в области ИИ можно представить в таком виде, надлежащим образом выбрав «сенсоры», «эффекторы» и «целевую функцию» (хотя не всегда этот выбор очевиден и естественен).
Так, робот, решающий какую-то задачу на производстве, или программа, играющая в шахматы, вполне прозрачно представляются в такой форме. Относительно агентов, обладающих общим интеллектом (таких как человек), аналогичный вывод сделать сложнее. Тем не менее, и человек «всего лишь» получает сенсорную информацию и совершает какие-то действия. Ничего сверх этого ему действительно недоступно. Оптимизирует ли он при этом какую-то целевую функцию? С эволюционной точки зрения, можно сказать, что да: это функция приспособленности. Пусть человек это делает и не сознательно (да и сама функция не задана в явном виде), но те организмы, выбор действий которыми не согласован с этой функцией, просто не выживали или не оставляли потомства.
Конечно, можно также сказать, что повышать выживаемость можно многими разными способами, в том числе и не интеллектуальными, например, совершенствованием тела, его «физических» характеристик. Некоторые виды успешно выживают на протяжении многих миллионов лет без использования развитого интеллекта, то есть интеллект для вполне успешной оптимизации их функции приспособленности оказывается не очень нужным. Это относится не только к функции приспособленности, но и к любой другой целевой функции: так, при создании системы распознавания каких-то объектов можно использовать простые неспециализированные сенсоры и интеллектуальные алгоритмы обработки сенсорной информации, а можно использовать сложные специализированные сенсоры, позволяющие выполнять распознавание с помощью элементарных алгоритмов. Таким образом, интеллект, хоть и не противоречит такой постановке (оптимизации целевой функции), но не сводится к ней. Не углубляясь в спор, насколько такая точка зрения справедлива, отметим просто, что все же от интеллектуального агента требуется выбор действий, и под любой конкретный способ выбора можно подобрать некоторую целевую функцию. В этом смысле можно считать, что интеллект оптимизирует некоторую функцию, для которой приспособленность является одним из компонентов или частным случаем. Вопрос здесь не в том, насколько такое представление в принципе допустимо, а в том, насколько оно удобно (и этот вопрос в отношении универсального интеллекта вовсе не праздный).
Другое сомнение может заключаться в том, что задание ограниченного перечня сенсоров и эффекторов для универсального интеллекта выглядит как необоснованное ограничение. Даже у человека (интеллект которого является все же в достаточной мере специализированным, а не абсолютно универсальным) это ограничение не столь жесткое. Человек очень широко использует инструменты для расширения набора своих сенсоров и эффекторов, которые он отчасти интерпретирует в качестве продолжения своего тела. Более того, даже на уровне возможна переориентация зон коры на обработку информации другой модальности. При этом, однако, число «входов» и «выходов» вовсе не меняется. Все изменения обусловлены структурой или контекстом соответствующей информации или действий, что в постановке задачи для универсального ИИ никак не запрещается. Конечно, наделение ИИ способностью непосредственного подключения инструментов как сенсоров и эффекторов новых модальностей может быть полезным, но вряд ли является принципиальным, по крайней мере, для текущего этапа анализа.
Еще один момент заключается в том, что при рассмотрении полностью воплощенного ИИ взаимодействие с миром может не ограничиваться только «штатными интерфейсами» тела агента – сенсорами, целевой функцией и эффекторами. Извне может оказываться произвольное воздействие и на саму программу интеллектуального агента. Иногда это рассматривается как существенный момент [Ring and Orseau, 2011]. Однако для человека такая ситуация означает непосредственное вмешательство в , которое обычно имеет не информационный, а физический (или химический) характер, и человеческих разум очень уязвим по отношению к таким вмешательствам. Конечно, можно поставить вопрос о создании универсального ИИ, который был бы более защищен от подобных воздействий, но в целом этот вопрос представляется не первоочередным.
Таким образом, одной из наиболее общих (хотя, возможно, не самой удачной) является следующая постановка задачи для универсального интеллекта. На вход агенту в каждый момент времени t по сенсорному входу подаются значения ot, принадлежащие некоторому множеству O, которое может иметь определенную структуру; от среды через «тело» поступают скалярные значения подкрепления rt, которые принадлежат заданному диапазону R=(rmin, rmax). Пару (ot, rt) будем обозначать для краткости xt, xt ∈ X = O × R. Также агент совершает действия yt (принадлежащие некоторому множеству Y) так, чтобы максимизировать суммарное значение целевой функции в будущем
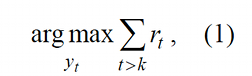
где k – текущий момент времени. Отметим, что здесь мы будем использовать обозначения, преимущественно заимствованные из [Hutter, 2005], поскольку представленная в данной работе модель универсального ИИ, является наиболее широко известной и может рассматриваться в качестве нулевого приближения к реальному сильному ИИ.
В данной формулировке (1) задача, очевидно, не является корректно поставленной: агенту необходимо максимизировать значения rt при t >k, о которых в условии задачи ничего не сказано. Иными словами, необходимо вводить хоть какие-то предположения о мире, которые бы позволили установить связь между предшествующими значениями ot, rt, yt и их будущими значениями.
Случай известного вычислимого мира
Рассмотрим сначала простейший случай среды, полностью описывающейся известной машиной Тьюринга (алгоритмом или программой для универсальной машины Тьюринга) q', входом которой на момент времени k являются действия агента y1,…, yk, а выходом – значения ok и rk. Сам агент также управляется некоторой программой p', входом которой являются o1r1,…ok–1rk–1, т.е. x1,…xk–1, а выходом – значение yk.
Для краткости последовательности вида ym…yn будем обозначать ym:n, а при m=1 будем писать y≤n или y<n+1. Для обозначения множества последовательностей, составленных из объектов множества Y, будет использовать традиционное обозначение Y*. Тогда программы q' и p' задают соответствующие отображения q′: Y* → X и p′: X * → Y, причем xk=q'(y≤k) и yk=p'(x<k). Также будем писать ok=qo'(y≤k) и rk=qr'(y≤k) для соответствующих компонентов xk. Здесь полагается, что на каждом такте времени программы запускаются поочередно: сначала запускается p', а потом – q', причем в начальный момент времени строка x<1 является пустой. Принципиальной асимметрии между средой и агентом здесь нет (за исключением начального момента времени), поскольку запуски p' и q' постоянно чередуются, и отнесение двух запусков к одному такту условно. Здесь, естественно, не принимается в расчет время вычисления p' и q', но в остальном такая постановка выглядит достаточно естественной. Нужно подчеркнуть, что никакого «реального времени» здесь в принципе нет: эти программы работают не постоянно, а вызываются на каждом такте заново. Тогда текущий результат взаимодействия агента с миром может быть вычислен в цикле:
для t от 0 до k: yt = p'(x<t), xt = q'(y≤t).
Чтобы избавиться от асимметрии (вернее, от полутактов), можно было бы xt считать как q'(y<t). С формальной точки зрения это приведет к постановке другой задачи. Так, исходная постановка с xt = q'(y≤t) подходит для описания игры в шахматы, но не в игру «камень-ножницы-бумага», тогда как вариант с xt = q'(y<t) – наоборот. Однако поскольку оба эти варианта не учитывают необходимость вычисления q' в масштабе реального времени, с введением которой различия между ними будут устранены, на данном этапе практически без разницы, какой из них использовать за исключением искусственных случаев типа упомянутых игр, правила которых определяют конкретную организацию последовательности «ходов» агента и среды (стоит также отметить некорректность варианта yt = p'(x≤t), xt = q'(y≤t)). Естественно, при реальной игре в «камень-ножницы-бумагу» абсолютной одновременности ходов нет, а есть ли она на уровне элементарных действий, практически не важно (здесь можно вспомнить о реально работающем роботе, который выигрывает в эту игру у человека за счет распознавания выбора человека до обозначения собственного выбора). Также и при реальной игре в шахматы очередность ходов может быть «физически» легко нарушена.
Для удобства также введем программы p и q, такие что x1:k=q(y≤k) и y1:k=p(x<k), то есть p – программа, которая не просто выбирает текущие действия, а возвращает всю их историю. Эквивалентные программы p и p' (q и q') могут быть легко получены друг из друга, поэтому их введение здесь – не более чем вопрос удобства. Поскольку формируемые строки из x и y зависят от обеих программ p и q в силу рекурсивности вызовов q(y≤k)=q(p(x<k))=q(p(q(y<k))), конкретный элемент истории, сформированной p и q, будем обозначать через, например, rtpq, y1:kpq и т.д.
Поскольку p и q детерминированы, можно для них посчитать будущий (после текущего момента k до некоторого момента m) суммарный выигрыш, который получит агент:
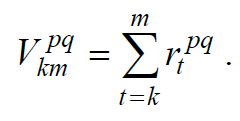
Теперь мы можем корректно поставить задачу определения лучшей политики p* и лучшего текущего действия:
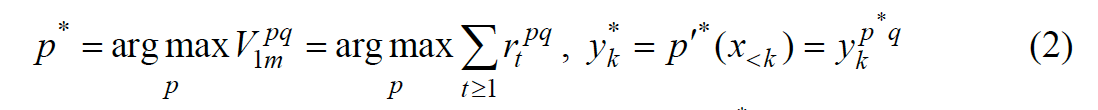
Решение задачи поиска оптимальной стратегии p* под конкретную среду q может быть выполнено априорно по формуле (2), хотя построение такого оптимального интеллектуального агента может быть весьма нетривиальным, так как непосредственно применить данную формулу на практике обычно невозможно из соображений вычислительной сложности.
Кажется, что программы p* для разных сред должны быть принципиально различными. В этой связи весьма примечательно, что существует универсальная программа выбора оптимальных действий по модели среды q. Собственно, уравнение (2) и задает такую программу. Но можно предложить и другую универсальную программу, которая выбирает оптимальные действия непосредственно, а не через поиск частной оптимальной программы. Такая программа задается следующим выражением:
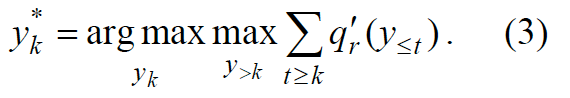
Действительно, если известная программа среды получает на вход цепочку действий агента, то можно производить поиск не программы p, порождающей оптимальную цепочку, а самой цепочки, и такой поиск как раз будет универсальной программой. Поскольку сама программа агента не зависит от программы среды q, а использует ее в качестве входных данных, она выглядит универсальной, и кажется, что прямой перебор при неограниченных ресурсах должен очевидным образом привести к максимизации q. Однако давайте обсудим адекватность постановки самой задачи, имея модель универсального интеллекта, по крайней мере, для известной среды.
Адекватность постановки задачи максимизации целевой функции
Одним из очевидных вопросов, которые здесь возникают, является выбор интервала времени (вернее, его верхнего предела), по которому производить суммирование. Этот вопрос, обойденный при записи уравнений (1)–(3), не имеет очевидного ответа и требует анализа. Посмотрим на традиционный пример шахматной позиции.
Идея здесь в том, что съедание белыми ладьи черных приведет к проигрышу. Ничья же достигается лишь в пределе. Никакая конечная глубина перебора не позволит переборному алгоритму «понять», что перманентный отказ от съедания ладьи эквивалентен ничьей. Это, правда, не помешает в данной ситуации агенту действовать адекватно: ведь при достаточной глубине перебора съедание будет за конечное число ходов приводить к проигрышу, поэтому оценка съедания ладьи будет ниже, чем любого другого (правда, агент не будет «понимать» эквивалентность сколь угодно долгое несъедание и ничьей). Кроме того, в практическом смысле агент не может существовать вечно, поэтому бесконечно длинная игра является не более чем абстракцией. Само время существования Вселенной является конечным, и сложно представить себе реалистичную ситуацию, когда у воплощенного агента глубина перебора должна быть неограниченной.
В то же время, с понятием бесконечности как элементом некоторого символьного представления такой агент тоже вполне сможет работать. А поскольку у человека символьные представления имеют семантическую основу в сенсорике и моторике, то есть просто являются какими-то комбинациями x и y, это должно быть в принципе доступно (хоть и не в явном виде) рассматриваемому агенту. Тем не менее, вполне возможно, что у понятия бесконечности какая-то выделенная семантическая основа, которая делает для человека рассуждения о бесконечных (в частности, циклических) процессах гораздо более естественными, чем для переборного алгоритма. Кроме того, безостановочные процессы имеют отношение к расширению классического понятия вычислимости (т.н. вычислимость в пределе), поэтому могут быть важным компонентом теории универсального интеллекта, что отмечается, например в [Schmidhuber, 2003]. Однако нас сейчас лишь интересует, будет ли наш агент действовать адекватно, а примеров очевидно неадекватного выбора действий нет.
Возвращаясь к вопросу о диапазоне времени суммирования, стоит отметить, что само принятие возможности ограничения этого диапазона не дает ответа на вопрос, как именно его нужно ограничивать. В частности, ограничение этого диапазона предполагаемым временем жизни агента ведет к неадекватному (вернее, нежелательному для людей) поведению. К примеру, такой агент ценою своей жизни не будет кого-либо спасать и вообще будет неизбежно действовать по принципу «после нас хоть потоп». Естественно, при создании сильного ИИ нужно будет решить проблему выбора надлежащего диапазона суммирования или, говоря более широко, желательной целевой функции, которая будет оценивать не только личную выгоду агента. В противном случае, экстраполяция этой функции на моменты времени после смерти агента будет давать всегда минимальные значения. Но получается, что целевая функция должна продолжать «существовать» в отсутствие самого агента.
На примере минимального интеллектуального агента особенно хорошо видна трудность задания целевой функции. Сам такой агент руководствуется лишь «сырыми данными» и выбирает цепочки элементарных действий. Никаких понятий он при этом в явном виде не использует, что не мешает ему действовать адекватно за счет исчерпывающего перебора. Но нам необходимо задавать целевую функцию, которая, как раз, и не выражается в показаниях простых датчиков. Для вычисления такой функции потребуется отдельный интеллект, причем не универсальный, а специализированный. Действительно, в случае простых миров, таких как шахматы, задание истинной целевой функции, определяемой правилами игры, вполне возможно; но если представить себе реальный мир, пусть для которого у нас есть точная физическая модель, позволяющая определять состояние мира в любой момент в будущем, перевести информацию об этом состоянии в значения целевой функции, определяемой хотя бы просто выживанием самого агента, будет очень непросто.
Если же целевая функция ограничивается лишь показаниями простых датчиков, в частности, болью и удовольствием, то следует ожидать эгоистичного поведения. Можно, конечно, «воспитывать» данного агента путем подкрепления и наказания. До тех пор пока у агента не будет средств устранить наказание, задаваемое людьми или другими интеллектуальными агентами, он будет действовать желаемым образом. Однако как только такой агент сможет предсказать отсутствие отрицательных для себя последствий, он будет действовать неэтично. Идея «воспитания» ИИ в целом правильная, но чтобы она сработала, необходимо, чтобы это воспитание не просто надстраивалось над имеющейся личной «телесной» целевой функцией, но и меняло ее.
Даже если игнорировать проблему обеспечения «дружественности» ИИ, а ставить перед ним просто задачу собственного выживания, максимизация априорной «телесной» целевой функции этой задаче не вполне удовлетворяет. Действительно, боль и удовольствие являются лишь эвристическими аппроксимациями эволюционной функции приспособленности. Они сродни оценке качества шахматных позиции на основе силы фигур. При этом в жизни, в отличие от шахмат, истинная целевая функция выживания не дана – мы не можем априорно определить, в какой именно ситуации будем живы или мертвы. Если и в шахматах руководствоваться только лишь грубой «телесной» оценкой, то уровень игры будет весьма далеким от оптимального. Также и животные (как, впрочем, в определенной степени и люди) могут максимизировать «телесную» целевую функцию в ущерб выживанию. Наиболее хорошо это видно на опытах, в которых крысам вживляли электроды в центры
удовольствия так, что животные могли их самостоятельно активировать. Поскольку целевая функция определяет лишь текущее качество состояния организма, ее экстраполяция не может в явном виде дать предсказание о смерти. Действие электрода увеличивает значение целевой функции нерелевантно истинному состоянию, в связи с чем поведение животного оказывается далеко неоптимальным. Таковым при определенных условиях может оказаться и поведение «универсального» искусственного интеллекта, перед которым поставлена задача максимизации врожденной целевой функции.
Существуют попытки предложить такие врожденные целевые функции, которые бы не приводили к вырожденному поведению [Ring and Orseau, 2011]. Можно рассмотреть гипотетические реакции агентов с разными целевыми функциями на разнообразные дилеммы. Скажем, согласится ли тот или иной агент на неограниченные по времени наслаждения в виртуальной реальности, из которой он не сможет выйти до конца своей жизни? Если же вспомнить неучтенную в простейшей постановке возможность модификации интеллекта самого агента, то перед ним можно поставить и еще более жесткую дилемму: неограниченное наслаждение ценой максимального упрощения интеллекта агента. Вполне очевидно, что интеллектуальный агент, максимизирующий сугубо «телесную» целевую функцию, сделает выбор, на который согласились бы далеко не все люди. В то же время, целевая функция может строиться и на основе работы самого интеллекта, например путем учета разнообразия получаемой информации. Существует мнение [Orseau and Ring, 2011], что агенты с подобной мотивацией не будут подвержены «неправильному» выбору в случае подобных дилемм при том, что к выживанию они будут стремиться как к необходимому условию осуществления познания. С традиционной эволюционной точки зрения, однако, скорее, наоборот, стремление к познанию является эвристикой в целевой функции выживания. Как видно, анализ данных проблем требует более детальных моделей универсального интеллекта.
Таким образом, модель максимизации заданной целевой функции не вполне универсальна; вернее, ее можно считать моделью универсального интеллекта, задача которого ограничивается лишь выполнением этой максимизации на фиксированном временном интервале. Но она не может считаться моделью интеллектуального агента в целом, частью которого является, в том числе, сама целевая функция, а задачей которого является, как
минимум, выживание. В конечном итоге нас интересует, конечно, создание интеллектуального агента (причем занимающегося не только выживанием). Мы, однако, пока ограничимся рассмотрением моделей лишь чистого интеллекта.
Неопределенная среда
Случай известной детерминированной среды с заданной целевой функцией банален. По сути, вся область ИИ началась с рассмотрения этого случая, когда была высказана лабиринтная гипотеза . И, естественно, исследователи очень быстро с общей постановки задачи перешли к вопросу о том, как ее решать на практике в условиях ограниченных вычислительных ресурсов. Вместе с тем заданность среды означает неавтономность и неуниверсальность соответствующих интеллектуальных программ. Так, удается создать программы, которые оказываются эффективнее человека в каждом из таких ограниченных миров, но это не позволяет компьютеру решать новые задачи самостоятельно. Вполне естественно желание сразу рассмотреть общий случай, включающий произвольную и неопределенную среду. Конечно, можно задаться вопросом, стоит ли браться за более сложную задачу, когда полное решение для более простой задачи детерминированной среды (при ограничении на ресурсы) отсутствует? Но в истории науки есть множество примеров, когда решение более простой, частной задачи не удавалось получить до тех пор, пока не была решена более общая задача. Здесь рассмотрение постановки задачи для более универсального интеллектуального агента, если и не приведет к своему полному решению, позволит лучше понять проблему ИИ в целом и облегчит решение чуть более частных задач.
Что означает отсутствие у нас полной информации о среде? Это означает, что мы не знаем в точности алгоритма среды q. Но что агенту о среде известно? Пусть существует некоторое множество алгоритмов, каждый из которых может оказаться истинным (это множество может быть алгоритмически полным). И пусть агенту дано распределение априорных вероятностей μ(q).
Введение такого распределения может показаться странным. Ведь рассматриваемые алгоритмические модели являются детерминированными и либо соответствуют среде, либо нет. Однако наименее противоречивой является не статистическая, а информационная интерпретация вероятности: вероятность событию, модели и т.д. приписывается постольку, поскольку у нас нет полной информации для их предсказания или выбора. Здесь же мы как раз и предполагаем неполную информацию о модели среды, и эта неполнота гибко описывается распределением вероятностей. Следует, однако, подчеркнуть, что распределение μ(q) нельзя считать «истинным»; корректнее его полагать наилучшим из возможных при имеющейся априорной информации. Хотя в некоторых условиях этому распределению вероятностей можно придать и вполне статистический смысл. К примеру, если «среда» – это противник при конкретной игре в шахматы, то априорные вероятности могут обозначать, например, частоту встречаемости противников, идеально играющих по принципу минимакса, профессионалов, новичков и т.д. В этом случае можно полагать, что есть некая генеральная совокупность противников-«сред», которая описывается «истинным» распределением μ(q), хотя некоторая доля условности остается и здесь.
Имея распределение вероятностей μ(q), несложно модифицировать постановку задачи для агента как максимизацию математического ожидания ожидаемого подкрепления:
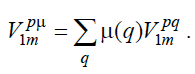
Опять же, это выражение не обладает оригинальностью и приведено здесь в соответствии, например, с [Hutter, 2005]. Оптимальная модель агента тогда будет определяться как
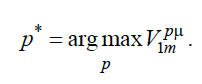
Казалось бы, данное выражение введено корректно. Интересно, однако, то, что программу p* нельзя выбирать априорно в соответствии с ним и оставлять неизменной. Как было подчеркнуто выше, сейчас мы рассматриваем детерминированные среды, поэтому распределение μ(q) не может иметь смысла истинной стохастической модели среды. Вместо этого, μ(q) – априорно лучшая неопределенная модель детерминированной среды.
Разницу между ними можно пояснить на примере бинарной последовательности, которая в одном случае порождается неизвестным детерминированным алгоритмом (генератором псевдослучайных чисел, ГПСЧ), а в другом – истинно случайным процессом с вероятностями P(0)=P(1)=0.5. Случайный процесс описывается вполне определенной стохастической моделью, которая может быть истинной. Сколько бы мы нулей и единиц ни наблюдали, на модель это никак не влияет. Напротив, в случае неопределенной детерминистской модели наблюдение части бинарной последовательности будет снижать неопределенность: не любой ГПСЧ может породить именно ту последовательность, которую мы наблюдаем, и часть из них мы можем исключить из рассмотрения.
Но если у нас есть некоторые q, которые не согласуются с уже имеющейся историей, разве может для них выполняться неравенство μ(q)≠0? Очевидно, нет. Поэтому распределение μ(q) и математическое ожидание подкрепления при имеющейся истории взаимодействия агента со средой должно пересчитываться. Для неопределенных детерминированных моделей можно принять простой способ пересчета для момента k:
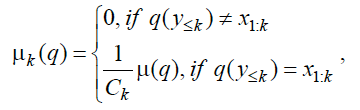
где Ck – константа (для имеющейся истории в момент k), обеспечивающая нормировку μk(q). Поскольку модели среды детерминированные, они не изменяют плавно своей вероятности, скажем, по правилу Байеса, а просто отсеиваются. Накладывает ли использование детерминированных программ p и q какие-то ограничения на универсальность интеллектуального агента? Вопрос этот неоднозначный, поскольку само наличие истинной случайности в реальном мире дискуссионно. А при том, что наименее противоречивая формализация понятия вероятности достигается в рамках алгоритмической теории информации, в нулевом приближении можно считать, что детерминированных моделей достаточно. К этому вопросу, однако, мы вернемся ниже.
Теперь несложно уточнить математическое ожидание подкрепления с учетом имеющейся истории и оптимальную стратегию на момент k:
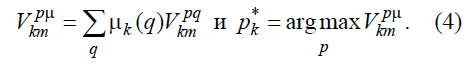
Здесь стоит особо оговорить смысл того, что в случае неопределенной среды не существует такого оптимального алгоритма p*, который при детерминированной среде мог быть построен по формуле (2) при k=1. Это достаточно простой, но принципиальный для понимания момент: кажется, что в случае неопределенной среды даже при данном распределении μ(q) нельзя (априорно) построить оптимальный алгоритм интеллекта, поскольку в зависимости от текущей истории он будет разным, то есть алгоритм p1*, определяемый по уравнению (4), будет неоптимальным при k >1. В то же время, сам выбор оптимальной программы, например в соответствии с уравнением (4), на каждом такте выглядит вполне алгоритмическим, то есть этот выбор осуществляется таким алгоритмом p1*, который остается оптимальным при k >1. Может показаться, что здесь есть некое противоречие. Однако его на самом деле нет. Просто алгоритмов, которые для текущего момента истории и данного распределения μ(q) дают максимальное значение математического ожидания будущего подкрепления, существует много. Какой именно из них возвращается по argmax в (4) не оговаривается. И этот алгоритм вполне может оказаться неоптимальным при поступлении новых данных. Однако среди всех оптимальных алгоритмов существуют и универсальные алгоритмы, в частности, выполняющие поиск других оптимальных алгоритмов по (4).
Естественно, существует универсальный алгоритм выбора оптимального действия, который перебирает не алгоритмы порождения действий, а непосредственно цепочки действий:
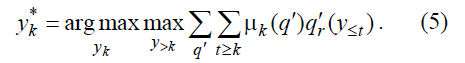
Очевидно, правая часть данного уравнения описывает универсальный алгоритм, который не меняется (меняется только значение его параметров) и сохраняет свою оптимальность для любого момента k.
В этой связи может показаться ненужным искать программы на каждом шаге в соответствии с (4), если у нас уже есть универсальная оптимальная программа в форме (5). Однако оптимальность последней будет нарушена, как только величина целевой функции станет зависеть от скорости работы алгоритма выбора действий, и построение универсального оптимального алгоритма вручную окажется проблематичным, и такой алгоритм окажется необходимым строить в процессе самооптимизации, для описания которой придется вернуться к поиску алгоритмов, что мы будем обсуждать позднее.
Уравнения (4) и (5) эквивалентны аналогичным уравнениям в [Hutter, 2005]. Здесь мы их приводим без уточнения, хотя полагаем их не вполне верными. Дело в том, что по (4) так же нельзя выбирать оптимальную программу pk*, как нельзя было априорно выбирать неизменную p1*. Данные уравнения не учитывают процесс изменения распределения μ(q) по мере накопления информации. В зависимости от выбора действия распределение μ(q) может оставаться неизменным или сужаться. Исследовательское поведение как раз и подразумевает выбор действий, нацеленных на получение информации, максимально снижающей неопределенность. Следует ожидать, что исследовательское поведение не будет свойственно агенту, действующему в соответствии с (4) и (5). Но здесь мы продолжим изложение по [Hutter, 2005].
Подчеркнем еще один аспект. Программа выбора оптимального действия является классическим алгоритмом, который запускается на определенных входных данных и формирует ответ. Однако действия интеллектуального агента в целом не являются классическим алгоритмом в том смысле, что система управления работает непрерывно и запускает алгоритм выбора действия на каждом такте с новыми данными. То есть данная система не работает с некоторой входной лентой, содержащей фиксированные исходные данные, по которым формируется некий конечный ответ. Напротив, система интерактивно взаимодействует со средой, функционирующей неформализованным образом и в процессе выполнения меняющей входные данные системы управления. В этом смысле данная система является не алгоритмом в строгом смысле этого слова, а алгоритмическим процессом (который также можно назвать «адаптивным алгоритмом»). Несмотря на очевидность данного обстоятельства, оно часто упускается из виду, в результате чего, в частности, к алгоритмическому интеллектуальному агенту некорректным образом применяется теорема Гёделя о неполноте формальных систем (в то же время, к агенту как открытой системе, взаимодействующей с неформальным миром, теорема Гёделя просто неприменима). Помимо этого интерактивность (адаптивность) этой системы может принять более сложную и не столь очевидную форму при развитии модели интеллектуального агента, поэтому данное формальное отличие от классического понятия алгоритма следует не упускать из вида.
В уравнении (5) по сравнению с (3) добавляется суммирование по всем заданным моделям сред, что делает задачу выбора оптимального действия вычислительно еще более тяжелой, но это является необходимым для универсальности агента. На данном этапе рассмотрения принципиальнее то, что априорное распределение для реального мира является недоступным.
Проблема универсального предсказания
Как строить модель универсального интеллектуального агента, если не дано μ(q)? Нужно вспомнить, что под μ(q) подразумевается не истинное, а некое лучшее (с учетом имеющейся априорной информации) распределение. Но в реальности это распределение построить крайне проблематично. Какое распределение стоит принять при минимуме априорной информации?
Пусть это распределение ξ. Для соблюдения универсальности необходимо, чтобы для любой программы q было верно ξ(q)≠0, то есть ни одна модель не отвергается априори. Максимальная непредвзятость должна была бы означать, что ξ(q)=const, но это невозможно, если полагать, что ξ(q) – (нормированное) распределение вероятностей. Даже если считать ξ(q) просто весами, с которыми та или иная модель учитывается при предсказании, такое решение привело бы к эффекту чрезмерно близкой подгонки (переобучения), что хорошо известно из практики при использовании метода максимального правдоподобия даже в случае алгоритмически неполных пространств моделей.
Адекватное решение дается в рамках алгоритмической теории информации, в которой не количество информации определяется по вероятности, а вероятность определяется по количеству информации, что, согласно А.Н. Колмогорову, должно иметь чисто комбинаторную основу. Как результат, вводится ξ(q)=2–l(q), где l(q) – количество двоичных символов в записи программы q. При использовании префиксных кодов или других кодов с саморазграничением суммарная вероятность 2–l(q) всех битовых строк (программ) оказывается равной 1.
Данное определение является весьма разумным: вероятность и количество информации связаны указанным соотношением, а количество информации в модели естественно определить через число бит в ее описании. Последнее, разумеется, вряд ли можно обосновать абсолютно строго; скорее, это определение имеет характер аксиомы, которая, однако, доказывает свою полную адекватность реальности. На этом можно было бы остановиться и просто использовать ξ(q) вместо μ(q), но необходимо сделать пояснения насчет того, что значимость универсального распределения ξ(q) выходит далеко за рамки его использования в (4) и (5).
В области машинного обучения, индукции и предсказания фундаментальный характер носит проблема априорных вероятностей. Ее игнорирование или неполное решение ведет к проблеме переобучения, которая свойственна большинству слабых методов машинного обучения, в том числе и искусственным нейронным сетям большинства типов. В рамках статистического подхода априорные вероятности при решении какой-то задачи могут определяться только по выборке задач данного класса, которые уже должны быть решены. Но даже в этом случае для оценивания априорного распределения вероятностей, заданного в какой-то форме, нужны будут априорные вероятности для самих распределений вероятностей. Это замкнутый круг, из которого статистическими методами выбраться принципиально нельзя. В итоге, априорное распределение, задающее (мета)модель, вводится эвристически разработчиком.
Аналогичная проблема видна и в классической теории информации: в ней количество информации в сообщении вводится как длина оптимального кода при известной (статистической) модели источника сообщений. При таких условиях оказывается невозможным определить ни индивидуальную вероятность, ни количество информации, скажем, в бинарной строке в условиях априорной неопределенности модели ее источника.
При такой неопределенности оказывается необходимым искать оптимальную модель источника информации в пространстве всех возможных моделей (в качестве которого выступает пространство алгоритмов). Но если знание оптимальной модели позволяет осуществлять наиболее эффективное сжатие, то обращение задачи оптимального кодирования должно позволять найти наилучшую модель. Иными словами, если нам нужно передать данные, закодированные наиболее компактным образом, то универсальный способ это сделать – передать наикратчайшую программу, воспроизводящую эти данные. Длина этой программы и будет количеством информации в этих данных, или, точнее, их Колмогоровской (алгоритмической) сложностью, а вероятность ξ(q) этой программы может быть приписана и данным. Однако с учетом того, что одни и те же данные могут быть порождены разными программами, априорную (алгоритмическую) вероятность соответствующей строки данных корректнее определить как сумму вероятностей всех этих программ. Таким образом, алгоритмическая сложность и алгоритмическая вероятность имеют вид:
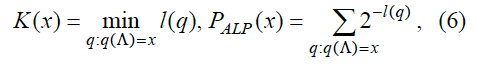
где Λ – пустая строка.
Стоит отметить, что в [Hutter, 2005] и [Hutter, 2007] обозначения для распределения вероятностей программ ξ(q)=2–l(q) и для алгоритмической вероятности произвольных строк PALP(x) смешиваются. Мы, однако, будем использовать разные обозначения.
Данный подход позволяет ввести базовое распределение априорных вероятностей, которое «разрывает» замкнутый круг оценки априорных вероятностей в статистическом подходе: если у нас на каком-то уровне статистического вывода отсутствует информация, необходимая для ввода априорных вероятностей, используем универсальные приоры. На основе алгоритмической вероятности можно построить [Solomonoff, 1986] универсальный метод предсказания. Несколько вольно можно записать алгоритмическую вероятность того, что имеющаяся строка x будет продолжена строкой x', как
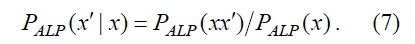
Вольность заключается в том, что в случае предсказания под PALP(x) следует понимать вероятность того, что некоторая программа породит не в точности строку x, а некую строку, для которой x является префиксом. Также и PALP(xx') – вероятность порождения строки, начинающейся с конкатенации xx'.
Здесь важно подчеркнуть, что универсальные вероятности, решающие проблемы статистического подхода, вводятся на основе чисто детерминированных моделей. Это говорит о том, что кажущееся игнорирование вероятностных моделей вовсе не сужает универсальности алгоритмического ИИ, при построении которого можно как будто вообще обойтись без понятия вероятности.
Тем не менее, это понятие весьма продуктивно и позволяет избежать некоторых рискованных шагов. К примеру, в [Hutter, 2005] можно встретить необоснованное предположение, что модель среды имеет конечную сложность. Это делает среду в точном смысле детерминированной. Но в то же время у нас нет никаких гарантий, что при неограниченном увеличении сенсорной истории x1:k обязательно наступит такой момент, что длина наикратчайшей программы q, способной воспроизвести эту историю, перестанет возрастать. Процесс, содержащий «истинную» случайность, как раз и характеризуется тем, что сложность порождаемых им данных неограниченно возрастает с ростом числа элементов в данных. С «практической» точки зрения, однако, не столь важно, является ли «истинная» случайность физически реальной или нет, поскольку сложность среды будет выше сложности накопленной агентом информации, и хотя бы поэтому момент стабилизации длины наикратчайшей адекватной программы q не наступит. И учет того, что точная модель среды q* будет иметь сложность, обязательно превышающую количество сенсорной информации агента (то есть не будет существовать такого момента, когда q* может быть реконструирована), может быть важным при развитии моделей алгоритмического ИИ.
Здесь мы не будем детально описывать все следствия из алгоритмической теории информации и вероятностей, поскольку они в достаточном объеме представлены во многих работах (см., напр., [Solomonoff, 1997], [Li and Vitanyi, 1997], [Потапов, 2007] и приведенные в них ссылки). Однако по мере необходимости будем обсуждать некоторые вопросы, важные для развития моделей алгоритмического ИИ.
В частности, в уравнении (6) упущен тот очевидный факт, что программы (алгоритмические модели) запускаются на некоторой универсальной машине U (или соответствуют некоторому способу программирования), в зависимости от которой длина одного и того же алгоритма будет разной. Для явного указания этого факта будем писать U(q) вместо q(Λ). Это ставит под сомнение универсальность распределения ξ(q).
Традиционный ответ на эту проблему заключается в том, что любая универсальная машина U может быть проэмулирована на другой машине V с помощью некоторой программа u, причем для любой программы q, V(uq)=U(q). Следовательно,
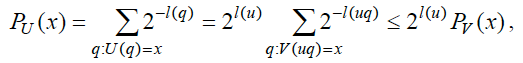
и аналогично Pv(x) ≤ 2l(v)PU(x), где PV, PU – алгоритмические вероятности, определяемые соответствующими машинами. То есть, задаваемые ими априорные вероятности будут отличаться не более чем на константный сомножитель. В этой связи говорят, что при достаточном объеме исходных данных зависимость индукции и предсказания от выбора опорной машины пропадает. Этот вывод нельзя сделать для неуниверсальной машины V, поскольку для нее будут существовать такие q, что PV(q)=0, то есть соответствующая модель будет непредставима и невыводима при использовании данной машины. В этом смысле, распределения, задаваемые разными универсальными машинами, являются оптимальными по Парето: если взять множество сред (описываемых алгоритмическими моделями), то любое универсальное распределение будет лучше (в плане предсказания) любого другого хотя бы в одной среде (или не хуже во всех средах). О распределениях, задаваемых неуниверсальными машинами, такого сказать нельзя. Отметим также, что если ограничиваться оптимальностью по Парето в указанном виде, то это означает безразличие к тому, насколько то или иное распределение оказывается эффективным в конкретном классе сред, то есть предсказание оказывается максимально непредвзятым (но не в смысле ξ(q)=const, а в смысле выбора самого ξ(q) независимо от среды).
Однако можно сразу заметить, что «достаточный объем данных» может оказаться очень большим, и его накопление будет нереалистично долгим. Этот вопрос относится к моделям универсального интеллекта следующих уровней детальности. Здесь же отметим, что правильнее говорить не о том, что выбор машины значения не имеет, а о том, что алгоритмические вероятности в случае разных машин являются ненулевыми для всех алгоритмических моделей, а также оказываются примерно одинаково «отсортированными». То есть нельзя задать априорные вероятности так, чтобы частичное упорядоченье моделей по вероятностям для обычной универсальной машины сменилось на противоположное. В этой связи можно сказать, что универсальным является не распределение априорных вероятностей, задаваемое какой-то одной опорной машиной, а сам способ их задания через сложность алгоритмов на универсальных машинах.
Модель AIξ
Модель AIξ [Hutter, 2005] получается из (4) и (5) путем подстановки ξ(q) вместо μ(q).
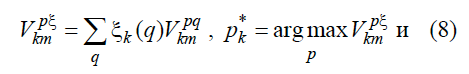
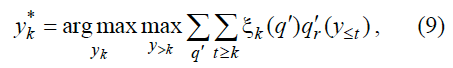
где ξk(q) определяется так же, как и μk(q).
Эту модель можно записать в разных формах. Можно не только заменить перебор программ агента p на перебор действий, но и ввести перебор по цепочкам ответов среды x>k, хотя в такой форме все равно придется перебирать q, но при этом будут в явном виде определяться вероятности для разных прогнозов данных x в форме (7). В этом случае алгоритм AIξ будет похож на построение дерева игры, но при неизвестной модели противника. Мы не будем приводить все формы этой модели (для этого можно обратиться к первоисточнику).
Пока не вводятся ресурсные ограничения, различия между разными формами этой модели не столь существенны. Подчеркнем лишь, что все варианты модели AIξ страдает от того же недостатка, что и формулы (4) и (5): в них не учитывается влияние выбора действий на возможное изменение распределения ξk(q). Этот дефект не так сложно исправить. Естественно, также нужно сразу понимать, насколько эта модель невообразимо далека от возможности реального воплощения. Ведь если агенту будет доступно всего два элементарных действия, совершающихся раз в секунду, с бинарным сенсором и рецептором боли, и то интеллектуальный агент, вычислительные ресурсы которого сопоставимы с человека, не сможет планировать больше, чем на минуту вперед. Любой прямой перебор программ или исчерпывающий перебор действий на практике недопустим.
Еще раз ответим на вопрос, почему же мы считаем такие модели принципиально необходимым отправным пунктом? Ответ заключается в том, что «практический» подход убедительно доказал свою несостоятельность в части построения сильного ИИ. В нем сразу теряется свойство универсальности, и «пост фактум» его не ввести, без чего ИИ будет принципиально ограниченным. Этот недостаток как раз и устраняется в моделях универсального алгоритмического интеллекта. Однако от завышения значимости простейших подобных моделей также нужно предостеречь, поскольку они столь же неэффективны, сколь и системы слабого ИИ неуниверсальны.
Стоит отметить, что модели типа AIξ достаточно очевидны с учетом универсального предсказания на основе алгоритмической вероятности. Заслуга Хаттера не столько во введении самой этой модели, сколько в детальном ее исследовании (включая вопросы ее оптимальности) и расширении.
Универсальность и однозначность ИМИ
Действительно ли модели ИМИ (модели типа AIξ) описывают универсальный интеллект? Мы уже видели, что постановка задачи для ИИ как максимизации целевой функции является неполной: сама проблема задания целевой функции оказывается весьма непростой (сюда можно включить и более частную проблему задания диапазона предсказания). Но является ли ИМИ универсальным хотя бы в плане решения этой задачи?
Здесь имеются разные тонкие аспекты. К примеру, алгоритмическая вероятность является невычислимой из-за проблемы останова. Мы уже отмечали, что результат, формируемый безостановочной моделью можно трактовать в смысле вычислимости в пределе. В зависимости от используемого понятия вычислимости безостановочные модели (а с практической точки зрения, просто долго работающие модели) могут учитываться или игнорироваться при вычислении алгоритмической вероятности. Этот аспект в будущем потребует уточнения.
Еще один упоминавшийся дискуссионный аспект модели ИМИ – это детерминированность. Рассмотрим элементарную игру – камень-ножницы- бумага (КНБ). У каждого игрока есть фиксированный набор действий, и есть однозначные правила выигрыша. Рассмотрим ее в случае конечной последовательности раундов.
Мы можем построить дерево вариантов (действие/ответ) заданной глубины для случая ok=q'(y<k), yk=p'(x<k); rk определяется через ok и yk. При k=1 дерево будет симметричным, то есть между действиями предпочтений не будет. Однако детерминированный алгоритм в таком случае будет выбирать какое-то действие однозначно, после чего симметрия нарушается. По истории раундов каждый противник будет пытаться восстановить программу другого противника. Для простоты предположим, что программы друг друга у противников совпадают и известны им априорно. Это могут быть программы, например, в форме (2). Но если программы детерминированные, то они определяют однозначную последовательность действий, а, значит, каждый противник может легко просчитать действия другого и сделать выигрышный выбор. Здесь видно явное противоречие. Ведь не могут же оба противника выиграть!
Действительно, противоречие есть. Оно очень простое, но весьма глубокое. Дело в том, что при расчете yk программа p запускает программу q, что очевидно, если программа p описывается уравнением (3). Но в данном случае программа q имеет такую же форму и запускает программу p, которая, в свою очередь, опять запускает программу q и т.д. Казалось бы, программа (3) включает конечное количество вызовов программы q. От среды мы неявно ожидаем, что она даст какую-то непосредственно вычисляемую реакцию на действие агента. Однако, как только в качестве среды рассматривается другой агент, программа которого включает запуск программы первого агента, получается бесконечная рекурсия, и в принципе никакого выбора действия сделать не получается. И даже бесконечное количество вычислительных ресурсов здесь не спасет. Значит, взаимодействие с другими интеллектуальными агентами – это принципиальный неучтенный аспект.
Конечно, можно подумать, что данный парадокс можно устранить, если снизить требование к «идеальности» ИИ, то есть рассмотреть более детальные модели с ограничением ресурсов. Можно сказать, что при ограниченных ресурсах какой-то выбор неизбежно будет сделан, но тогда детерминированный агент с меньшими ресурсами будет проигрывать в КНБ агенту с превосходящими ресурсами. В то же время существует банальная стратегия в КНБ, обеспечивающая в среднем ничью без каких-либо вычислительных затрат против противника со сколь угодно большими ресурсами: это выбор истинно случайного (но не псевдослучайного) действия, что полностью отсутствует в AIξ.
Как отмечалось, наличие в мире истинной случайности дискуссионно, но на практике реализовать датчик, который позволит агенту порождать последовательность чисел увеличивающейся алгоритмической сложности, не составит труда. Также стоит отметить, что пример КНБ вовсе не надуманный. При взаимодействии таких агентов, как хищник и жертва, в процессе погони случайность выбора траектории имеет столь же большое значение.
Итак, можно предположить, что у агента должна быть возможность совершать случайный выбор, что в принципе нельзя заменить детерминированным алгоритмом (что видно на примере рассмотренной игры КНБ в частности, и при взаимодействии с другими агентами в общем). Если же мультиагентная среда, в которой находится ИИ, характеризуется стохастическим алгоритмом, то это не помешает учитывать и при построении ее моделей, которое неминуемо должно включать абстрагирование (построение принципиально неполных/неточных моделей). Такое абстрагирование нужно не только при ограничении на ресурсы, но и в случае неограниченных ресурсов для устранения указанного противоречия, возникающего, когда p и q используют точные модели друг друга (из конструктивистских соображений очевидно, что агент не может точно моделировать мир, включающий самого агента, так как агент не может быть сложнее самого себя).
Здесь возникает также естественный вопрос, будет ли ИМИ обладать рефлексией, самосознанием? Можно задать и более объективистский вопрос: сможет ли ИМИ корректно пользоваться такими понятиями, как «думаю», «знаю»? С одной стороны, потребность в рефлексии в явном виде отсутствует в постановке задачи для ИМИ, и можно полагать, что ее с необходимостью придется ввести при рассмотрении ресурсных ограничений. С другой стороны, если предположить наличие неограниченных ресурсов у ИМИ, то это не избавит его от необходимости в конкретном социальном окружении применять понятия, связанные с собственным . Поскольку ИМИ может построить любой алгоритм и выбрать любое действие, увеличивающее целевую функцию, то можно полагать, что опосредованно использовать эти понятия он сможет (при наличии достаточно длинной истории взаимодействия), но непосредственной семантической основы у него для них не будет.
Можно поставить под сомнение достаточность алгоритмических моделей мира в целом. Хорошо известно мнение, что такие когнитивные функции, как понимание или самосознание связаны с невычислимыми физическими процессами. Опровергнуть это мнение можно, разве что, созданием сильного ИИ (и то кто-то не согласится приписать ему самосознание или понимание даже в этом случае), однако, и аргументация в его пользу весьма спорная. Поскольку этот вопрос широко обсуждается, здесь мы не будем уделять ему внимания, а лишь отметим, что даже если указанное мнение и верно, создание «алгоритмически универсального» ИИ будет существенным шагом вперед, и, кроме того, сейчас не существует технических средств, которые бы могли воплощать полезные для интеллекта невычислимые процессы.
Выводы
Модели идеального минимального интеллекта представляют собой теоретически оптимальный (при определенных оговорках) вариант выбора действий для максимизации целевой функции по истории взаимодействия со средой с использованием универсального предсказания на основе алгоритмической вероятности в априорно неопределенной среде. Заданность целевой функции, классическая вычислимость алгоритмов, недоучет мультиагентных взаимодействий, детерминированность в выборе действий, использование точных моделей среды, недоучет возможности снижения неопределенности в моделях мира при выборе действий, отсутствие рефлексии – это те особенности рассмотренной модели ИМИ, которые ставят под сомнение ее универсальность. Однако эти аспекты выглядят менее серьезными, чем проблема неэффективности (или даже невычислимости) данной модели. Кроме того, детальнее их проанализировать можно будет после ввода ресурсных ограничений.
Литература
(Hutter, 2005) Hutter M. Universal Artificial Intelligence. Sequential Decisions Based on Algorithmic Probability / Springer. 2005. 278 p.
(Hutter, 2007) Hutter M. Universal Algorithmic Intelligence: A Mathematical Top→Down Approach // in Artificial General Intelligence. Cognitive Technologies, B. Goertzel and C. Pennachin (Eds.). Springer. 2007. P. 227–290.
(Li and Vitanyi, 1997) Li M., Vitanyi P. An Introduction to Kolmogorov Complexity and Its Applications. 2nd ed: N.Y., Springer-Verlag. 1997.
(Orseau and Ring, 2011) Orseau L, Ring M. Self-Modification and Mortality in Artificial Agents // Lecture Notes in Computer Science 6830 (proc. Artificial General Intelligence – 4th International Conference). Springer, 2011. P. 1–10.
(Ring and Orseau, 2011) Ring M., Orseau L. Delusion, Survival, and Intelligent Agents // Lecture Notes in Computer Science 6830 (proc. Artificial General Intelligence – 4th International Conference). Springer, 2011. P. 11–20.
(Schmidhuber, 2003) Schmidhuber J. The new AI: General & sound & relevant for physics. Technical Report TR IDSIA-04-03, Version 1.0, cs.AI/0302012 v1, IDSIA. 2003.
(Solomonoff, 1986) Solomonoff R. The Application of Algorithmic Probability to Problems in Artificial Intelligence // In: L.N. Kanal and J.F. Lemmer (Eds.). Uncertainty in Artificial Intelligence: Elsevier Science Publishers. 1986. P. 473-491.
(Solomonoff, 1997) Solomonoff R. Does Algorithmic Probability Solve the Problem of Induction? // Oxbridge Research, P.O.B. 391887, Cambridge, Mass. 02139. 1997.
(Потапов, 2007) Потапов А.С. Распознавание образов и машинное восприятие: общий подход на основе принципа минимальной длины описания. СПб: Политехника, 2007. 548 с.
Автор: aideus
