Игра 15

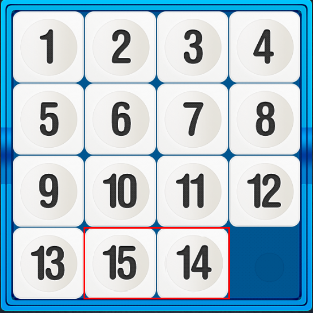
В начале 1880 года, некий Чарльз Певи, дантист из Вустера, привлёк внимание общественности предложив $1000 (тогда это были неплохие деньги), за решение следующей задачи: пятнадцать шашек были размещены в квадратной коробочке в правильном порядке, и только шашки 14 и 15 были переставлены, как показано на рисунке. Задача состояла в том, чтобы, последовательно передвигая шашки, привести их в нормальное положение, причем, однако, порядок шашек 14 и 15 должен быть исправлен.

У нас в компании каждый сотрудник может 5 часов в неделю заниматься самообразованием (читать/писать на «Хабр», учить F# или читать SICP). Со временем данная практика эволюционировала в создание мини-проектов. Так, например, Максим, опытный JavaScript-разработчик, решил попробовать себя в создании приложений под iOS, и, примерно, за полтора месяца выпустил пятнашки, которые, без всякой рекламы, за неделю продаж вошли в TOP 10 русского App Store в категории игры.

Далее код проверки на Objective-C и принцип прохождения пятнашек из книги Якова Исидоровича Перельмана «Живая математика».

Для многих из нас стало неожиданностью, что ровна половина из всех возможных (1 307 674 368 000) комбинаций, не имеет решений. Для проверки на решаемость мы взяли формулу из википедии: пусть квадратик с числом i расположен до (если считать слева направо и сверху вниз) k квадратиков с числами меньшими i. Будем считать n_i = k, то есть если после костяшки с i-м числом нет чисел, меньших i, то k = 0. Также введем число e — номер ряда пустой клетки (считая с 1). Если сумма

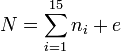
является нечётной, то решения головоломки не существует.

Код проверки на Objective-C

#import "GamePositionValidator.h"
@interface GamePositionValidator(){
	NSInteger  emptyCellRowNumber;
}
@property (nonatomic, retain) NSArray* validPosition;
@property (nonatomic, retain) NSArray* currentPosition;
@end
@implementation GamePositionValidator
@synthesize validPosition;
@synthesize currentPosition;
 
-(id) initWithValidPosition:(NSArray *) _validPosition emptyCellRowNumber:(NSInteger ) _emptyCellRowNumber{
	if(self = [super init]){
        self.validPosition = _validPosition;
        emptyCellRowNumber = _emptyCellRowNumber;
	}
	return self;
}
-(NSInteger) positionOfChipInValidPosition:(NSInteger) chipNumber{
	for(NSInteger i=0; i<self.validPosition.count; i++){
    	NSNumber* number = [self.validPosition objectAtIndex:i];
        if(number.intValue == chipNumber){
        	return i;
    	}
	}
	return -1;
}
 
-(NSInteger) countOfDisordersInPosition:(NSInteger) position{
	NSInteger chipNumber = ((NSNumber*)[self.currentPosition objectAtIndex:position]).intValue;
	NSInteger chipPosition = [self positionOfChipInValidPosition:chipNumber];
	NSInteger countOfDisorders = 0;
 
	for( NSInteger i= position+1; i<15; i++){
    	chipNumber = ((NSNumber*)[self.currentPosition objectAtIndex:i]).intValue;
    	NSInteger nextChipPosition = [self positionOfChipInValidPosition:chipNumber];
    	if( nextChipPosition < chipPosition){
            countOfDisorders ++;
   	 }
	}
 
	return countOfDisorders;
}
 
-(BOOL) isPositionCanBeTransformedToValidPosition:(NSArray*) position{
    self.currentPosition = position;
	NSInteger totalDisorders = 0;
	for(NSInteger i=0; i<self.currentPosition.count; i++){
    	totalDisorders+=[self countOfDisordersInPosition:i];
	}
    self.currentPosition = nil;
	return (totalDisorders + _emptyCellRowNumber) % 2 == 0;
}
@end

Это первое приложение Макса на Objective-C так что его можно смело критиковать.

На последок, принцип прохождения «пятнашек» в книге Я.И.Перельмана «Живая математика»:
«Представьте расположение, при котором 15 шашек размещены в пестром беспорядке. Рядом передвижений всегда можно привести шашку 1 на место. Точно так же возможно, не трогая шашки 1, привести шашку 2 на соседнее место вправо. Затем, не трогая шашек 1 и 2, можно поместить шашки 3 и 4 на их нормальные места: если они случайно не находятся в двух последних вертикальных рядах, то легко привести их в эту область и затем рядом передвижений достичь желаемого результата.
Теперь верхняя строка 1, 2, 3, 4 приведена в порядок, и при дальнейших манипуляциях с шашками мы трогать этого ряда не будем.

Таким же путем стараемся мы привести в порядок и вторую строку: 5, 6, 7, 8; легко убедиться, что это всегда достижимо. Далее, на пространстве двух последних рядов необходимо привести в нормальное положение шашки 9 и 13; это тоже всегда возможно. Из всех приведенных в порядок шашек 1, 2, 3, 4, 5, 6, 7, 8, 9 и 13 в дальнейшем ни одной не перемещают;

остается небольшой участок в шесть полей, в котором одно свободно, а пять остальных заняты шашками 10, 11, 12, 14, 15 в произвольном порядке. В пределах этого шестиместного участка всегда можно привести на нормальные места шашки 10, 11, 12. Когда это достигнуто, то в последнем ряду шашки 14 и 15 окажутся размещенными либо в нормальном порядке, либо в обратном». Удачи!

Автор: AnthonyBY