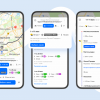
Остается всё меньше людей, которых можно удивить дополненной реальностью (AR). Для кого-то эта технология ассоциируется с игрушкой на пару часов. Другие находят ей более практичное применение.

Меня зовут Дмитрий, и я разрабатываю Яндекс.Карты для iOS. Сегодня я расскажу читателям Хабра о том, как мы создавали маршрутизацию с использованием дополненной реальности. Вы также узнаете об особенностях применения фреймворка ARKit, благодаря которому внедрение дополненной реальности перестало быть уделом лишь специалистов в области компьютерного зрения.

В 2009 году журнал Esquire первым среди изданий масс-медиа добавил поддержку дополненной реальности в свой продукт. На обложке журнала разместили код, с помощью которого можно было увидеть Роберта Дауни младшего "вживую".

Применение AR в сфере развлечений этим не ограничилось. Ярким примером стала игра Pokemon Go, вышедшая в 2016 году. Уже к июлю того же года её скачали свыше 16 млн раз. Успех игры привёл к появлению многочисленных клонов с AR.

Значимыми событиями в индустрии AR за последние годы можно считать анонсы Google Glass и Microsoft Hololens. Появление подобного рода устройств показывает вектор, в котором движутся крупные компании.

Не стала исключением и Apple. В 2017 году компания представила фреймворк ARKit, значение которого для индустрии трудно переоценить. И о нём мы расскажем подробнее.

ARKit

Особенности ARKit, благодаря которым использовать AR стало просто:

• отсутствие необходимости в специальных метках (маркерах),
• интеграция с существующими фреймворками для 2D/3D графики от Apple – SceneKit, SpriteKit, Metal,
• высокая точность определения позиции и ориентации устройства в пространстве,
• отсутствие необходимости в калибровке камеры или датчиков.

Под капотом ARKit находится система визуально-инерциальной одометрии, которая объединяет данные с визуальной (камера) и инерциальной (акселлирометр, гироскоп) подсистем устройства для определения положения и смещения на сцене. Связующим элементом этой системы является фильтр Калмана – алгоритм, которые в каждый момент времени выбирает лучшее из показаний двух подсистем и предоставляем его нам в виде нашей позиции и ориентации на сцене. ARKit также обладает «пониманием» сцены – мы можем определять горизонтальные и вертикальные поверхности, а также условия освещенности сцены. Таким образом при добавлении на сцену объекта, мы можем добавить ему дефолтное освещение, благодаря которому объект будет выглядеть более реалистично.

ARKit позволил разработчикам внедрять в свои приложения дополненную реальность высокого качества, затрачивая при этом гораздо меньше усилий. Продемонстрируем это на примере Яндекс.Карт.

Маршрутизация с AR в Яндекс.Картах

Обычно, после анонса новой версии iOS многие команды в Яндексе собираются для обсуждения возможности внедрения новых фич в свои приложения. Команда Яндекс.Карт поступила так же. В течение месяца с момента анонса ARKit мы нередко обсуждали способы его внедрения в Карты. Каких только идей мы не наслушались друг от друга! Достаточно быстро мы пришли к выводу, что одним из самых полезных и лежащих на поверхности решений является использование дополненной реальности в маршрутизации.

Выбор данной идеи был обусловлен тем, что многие пользователи карт нередко сталкиваются с ситуацией, когда ты оказываешься в незнакомой местности и нужно быстро определиться куда идти. Стандартный подход для среднестатистического пользователя карт – открыть приложение, построить пешеходный маршрут, и, поворачиваясь на месте, определить, куда нужно двигаться. Идея внедрения дополненной реальности в пешеходную маршрутизацию – избавить пользователя от лишних действий, сразу показав, куда нужно двигаться прямо поверх изображения с камеры.

Для начала хочу сказать пару слов о маршрутизации. Что я закладываю в это понятие? С точки зрения реализации в мобильном приложении, это достаточно стандартный набор шагов, позволяющих пользователю добраться из точки A в точку B:

• выбор точек отправления и прибытия,
• получение маршрута в виде набора точек в географических (широта, долгота) координатах,
• отображение на карте линии маршрута,
• сопровождение пользователя дополнительной информацией во время движения по маршруту.

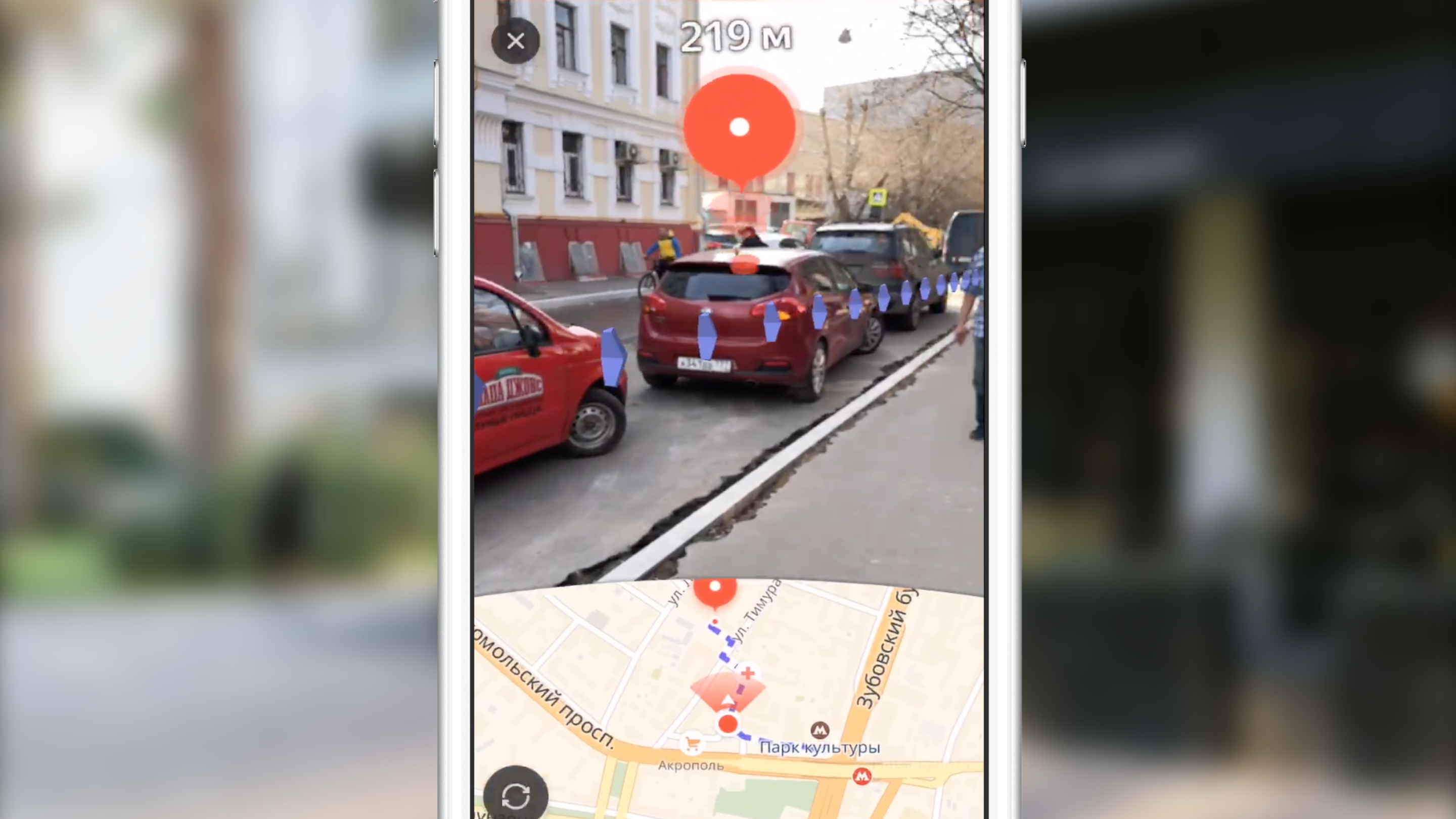
Мы не будем останавливаться на первых двух пунктах. Скажу только, что мы получаем маршрут через нашу кроссплатформенную библиотеку Яндекс.Mapkit, которая доступна и вам в виде pod’а. Чем же маршрутизация с дополненной реальностью отличается от стандартной маршрутизации в картах? В первую очередь основным отличием является почти полностью скрытая карта. Основной упор делается на область экрана с изображением видеопотока с камеры, на которую накладываются дополнительные визуальные элементы (метка финиша, вспомогательная метка и изображение линии маршрута). Каждый из этих визуальных элементов обладает своей смысловой нагрузкой и своей логикой (когда и как он должен быть отображен). Мы рассмотрим роль каждого из этих элементов более подробно позднее, а пока предлагаю рассмотреть задачи, которые стояли перед нами изначально:

• научиться позиционировать объекты на сцене ARKit, зная их географические координаты,
• научиться отрисовывать необходимый UI на 3D сцене с достаточной производительностью.

Нам было нужно сконвертировать координаты точек из географических в координаты на сцене, выбрать, какие из точек отображать, и отобразить весь необходимый UI поверх изображения камеры в правильной позиции. Но всё оказалось немного сложнее, чем показалось на первый взгляд.

Перед тем как приступить к реализации непосредственно фичи, одному из моих коллег была дана задача сделать прототип, показывающий возможность (или невозможность) реализации подобной функциональности с доступным набором инструментов. В течении двух недель мы наблюдали Сан-Саныча бороздившим просторы опенспейса и близлежащих окрестностей нашего офиса с телефоном в руках и рассматривающим окружающий мир сквозь призму камеры. В итоге мы получили работающий прототип, который показывал каждую точку маршрута в виде метки на сцене с расстоянием до нее. С помощью этого прототипа можно было при удачном стечении обстоятельств дойти от работы до метро и даже почти не заблудиться. А если серьезно, он подтвердил возможность реализации задуманной функциональности. Но оставался ряд задач, которые нашей команде ещё предстояло решить.

Началось всё с изучение инструментов. На тот момент только один человек в команде имел опыт в работе с 3D графикой. Давайте кратко рассмотрим те инструменты, с которыми придется столкнуться любому, кто задумается о реализации подобных идей с помощью ARKit.

Инструменты и API

Основная работа по рендерингу объектов заключается в создании и менеджменте объектов сцены фреймворка SceneKit. С появлением ARKit разработчику стал доступен класс ARSCNView (наследник класса SCNView – базового класса для работы со сценой в SceneKit), который решает большинство трудоемких задач по интеграции ARKit и SceneKit, а именно:

• синхронизация положения телефона в пространстве с положением камеры на сцене,
• система координат сцены совпадает с системой координат ARKit,
• в качестве background'а сцены используется видеопоток с камеры устройства.

Также объект ARSCNView предоставляет разработчику объект сессии дополненной реальности, которую можно запустить с необходимой конфигурацией, остановить или подписаться на различные ее события используя объект делегата.

Для добавления на сцену объектов используется наследники или непосредственно объекты SCNNode. Этот класс представляет позицию (трехмерный вектор) в системе координат своего родительского объекта. Таким образом мы получаем дерево объектов на сцене с корнем в специальном объекте – rootNode нашей сцены. Здесь все очень похоже на иерархию объектов UIView в UIKit. Объекты SCNNode могут быть отображены на сцене при добавлении им материала и освещения.

Для того, чтобы добавить дополненную реальность в мобильное приложение, необходимо также знать об основных объектах API ARKit. Главным из них является объект сессии дополненной реальности – ARSession. Этот объект осуществляет процессинг данных и отвечает за жизненный цикл сессии дополненной реальности. Целью данной статьи не является пересказ документации ARKit и SceneKit, поэтому я не буду писать обо всех доступных параметрах конфигурации сессии дополненной реальности, а остановлюсь на одном из важнейших для навигационных приложений параметре конфигурации сессии дополненной реальности – worldAlignment. Этот параметр определяет направление координат осей сцены в момент инициализации сессии. Вообще, при инициализации сессии дополненной реальности, ARKit создает систему координат с началом в точке, совпадающей с текущим положением телефона в пространстве, и направляет оси этой системы в зависимости от значения свойства woldAlignment. В нашей реализации используется значение gravityAndHeading, которое подразумевает, что оси будут направлены следующим образом: ось Y – в направлении противоположном гравитации, ось Z – на юг, а ось X – на восток.

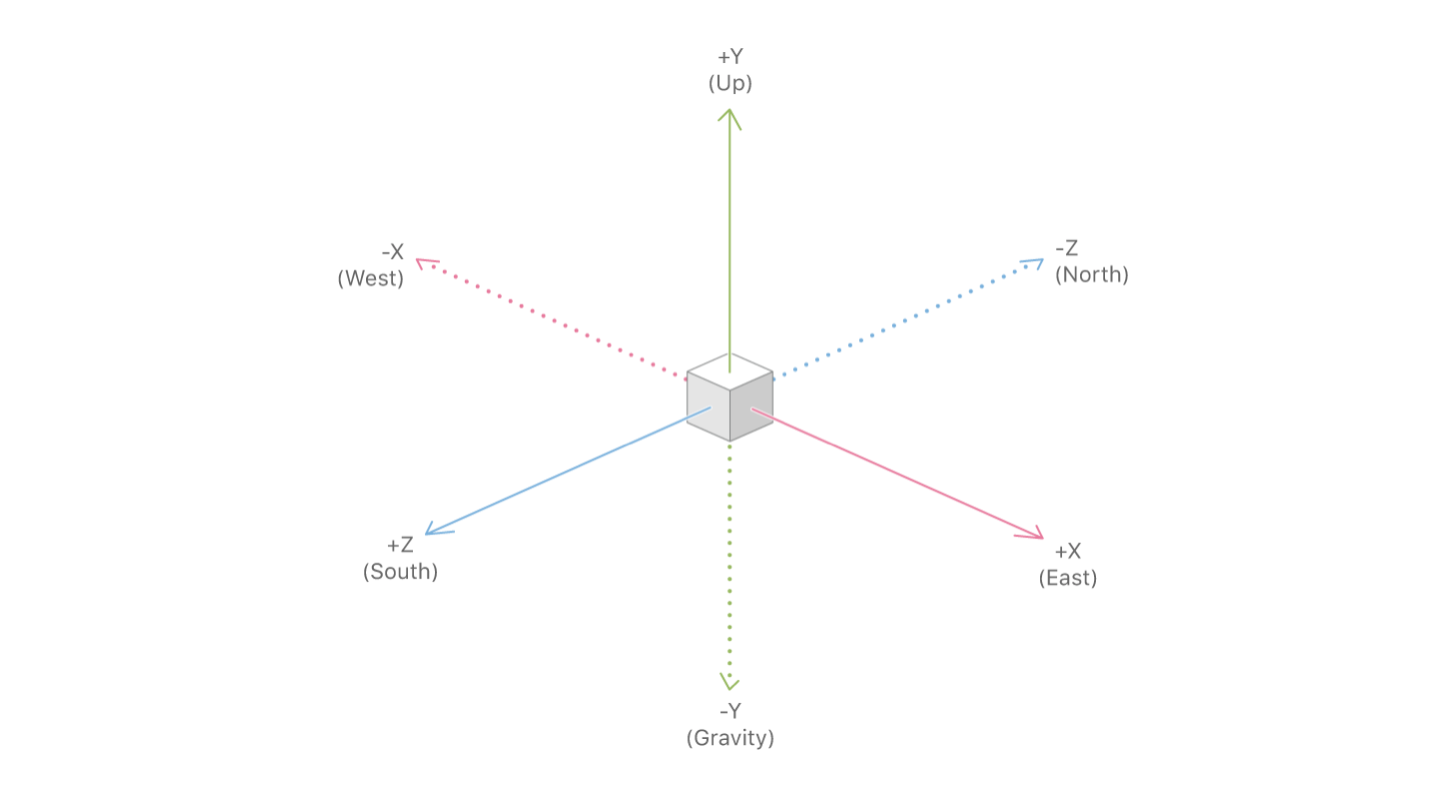
При удачном стечении обстоятельств оси X/Z действительно будут сонаправлены с направлениями на Юг/Восток, но, из-за погрешностей в показаниях компаса, оси могут быть направлены под некоторым углом к направлению, описанному в документации. Это одна из проблем, с которой нам предстояло бороться, но об этом чуть позже.

Теперь, когда мы рассмотрели основные инструменты, подведем краткий итог: отображение маршрута с использованием SceneKit – это добавление объектов SCNNode на сцену в позиции, полученные путем конвертации из географических координат в координаты сцены. Перед тем как поговорить о конвертации координат и в целом о размещении объектов на сцене давайте поговорим о проблемах отрисовки элементов UI, предполагая, что мы знаем позиции объектов на сцене.

Метка финиша

Главным визуальным элементом пешеходной маршрутизации с дополненной реальностью является метка финиша, отображающую конечную точку маршрута. Также над меткой мы показываем пользователю расстояние до конечной точки маршрута.

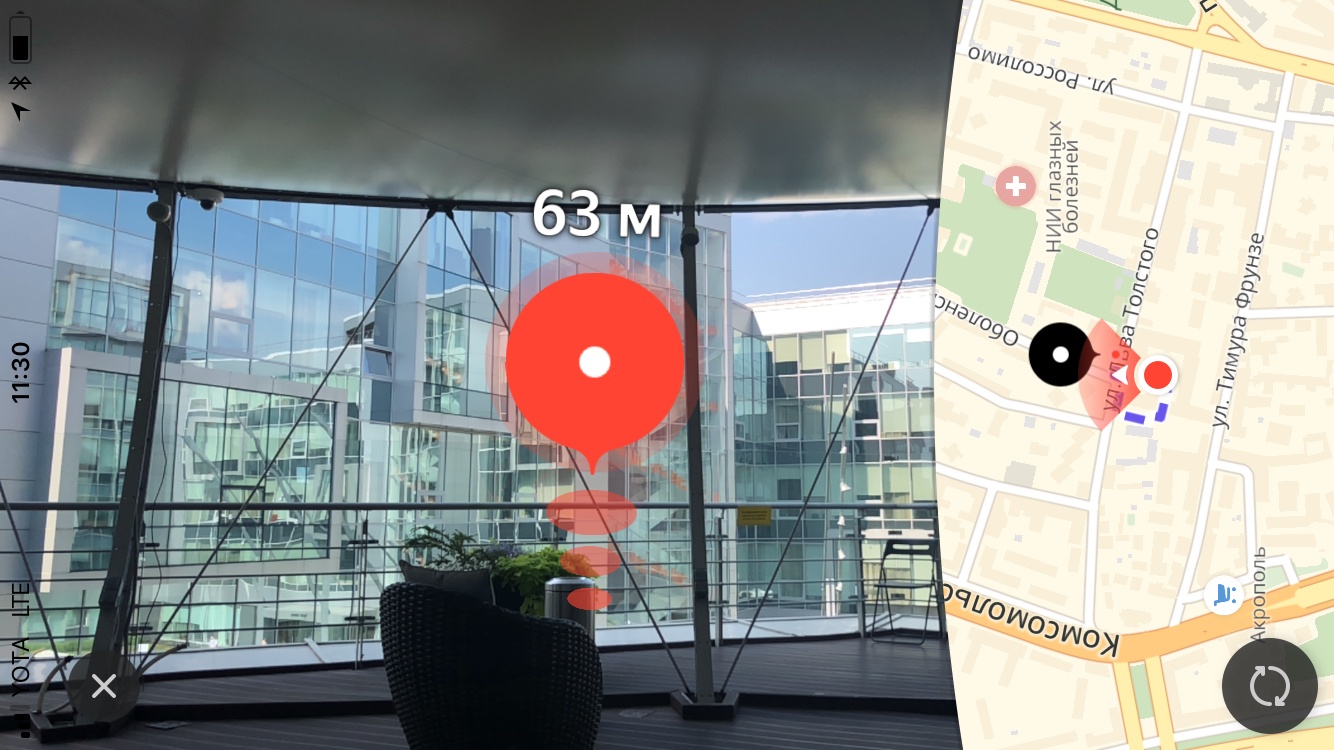
Размер

Когда нам впервые показали дизайн этой метки, то в первую очередь обратили внимание на требования к размеру этой метки. Они не подчинялись правилам перспективной проекции. Поясню, что в трехмерных движках, которые используются для создания, например, компьютерных игр, «взгляд» моделируется с помощью перспективной проекции. По правилам перспективной проекции удаленные предметы изображаются в меньших масштабах, а параллельные прямые в общем случае не параллельны. Таким образом размер проекции объекта на плоскость экрана изменяется линейно (уменьшается) при отдалении камеры от объекта на сцене. Из описания макетов вытекало, что размер метки на экране имеет фиксированный (максимальный) размер при удалении меньше 50 м, затем линейно уменьшается от 50 м до 2 км, после чего остается неизменного минимального размера. Такие требования обусловлены, очевидно, удобством для пользователя. Они позволяют пользователю никогда не терять конечную точку маршрута из вида, таким образом пользователь всегда будет иметь представление о том, куда двигаться.

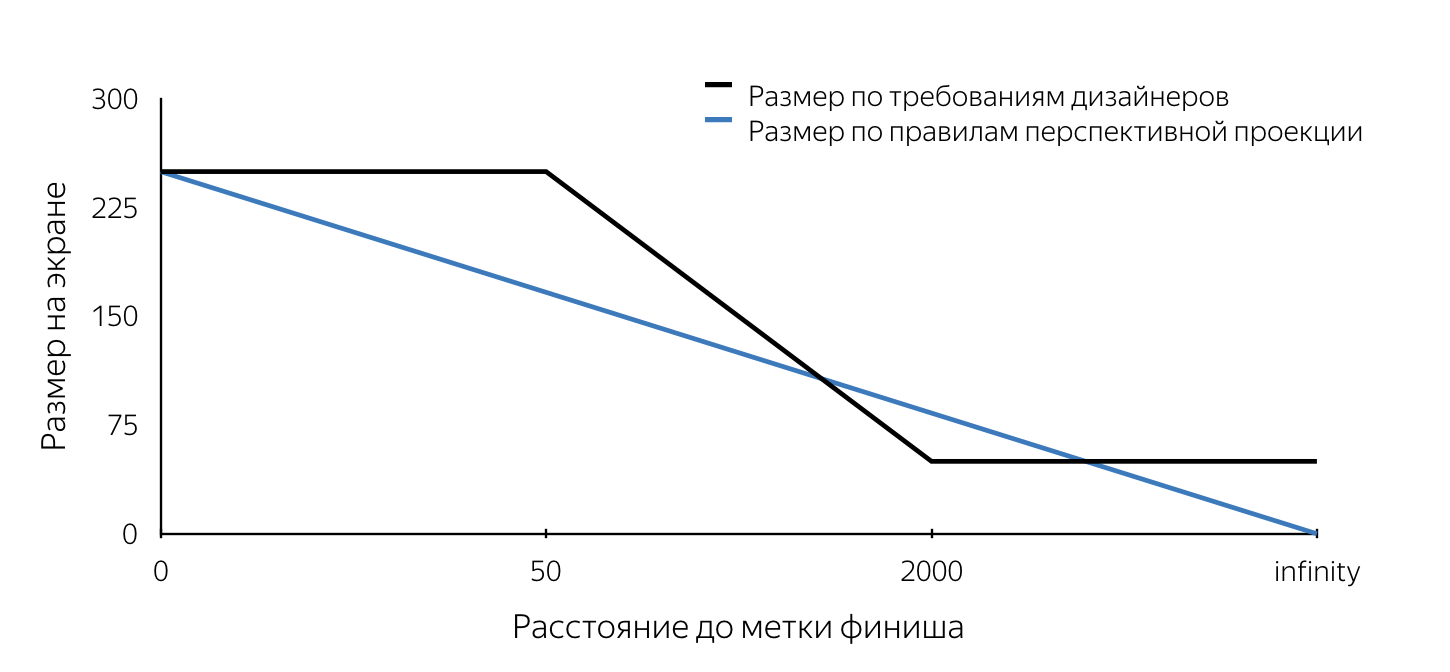
Нам предстояло понять, каким способом можно вклиниться в работающий по определенным правилам механизм проецирования SceneKit. Сразу хочу отметить, что на всё про всё у нас было около двух недель, поэтому времени производить глубокий анализ различных подходов к решению поставленных задач просто не было. Теперь, анализируя наши решения, оценивать их намного проще, и можно сделать вывод, что большинство принятых решений оказались верными. Требование к размеру, по сути, стало первым камнем преткновения. Все изложенные далее проблемы могут быть решены как с помощью SceneKit, так и UIKit. Я постарался подробно изложить способы решения каждой из проблем с использованием обоих подходов. Какой подход использовать, решать только вам.

Давайте представим, что мы решили реализовать метку финиша с использованием SceneKit. Если учесть, что метка по макетам должна была выглядеть на экране как окружность, то становится очевидно, что в SceneKit объект метки должен быть сферой (так как проекция сферы на любую плоскость является окружностью). Для того, чтобы проекция имела на экране определенный радиус, заданный в требованиях дизайнеров, необходимо в каждый момент времени знать радиус сферы. Таким образом, разместив сферу определенного радиуса на сцене в определенной точке и постоянно обновляя ее радиус при приближении или отдалении мы получим проекцию на экран необходимого размера в каждый момент времени. Алгоритм определения радиуса сферы в произвольный момент времени выглядит следующим образом:

1. определим положение объекта на сцене – центр сферы,
2. найдем проекцию этой точки на плоскость экрана (используя API SceneKit),
3. для определения необходимого размера метки на экране, найдем расстояние от камеры до центра сферы на сцене,
4. определим необходимый размер на экране по расстоянию до объекта, используя правила описанные в дизайне,
5. зная размер метки на экране (диаметр окружности), выберем любую точку на этой окружности,
6. сделаем обратное проецирование (unprojectPoint) выбранной точки,
7. найдем длину вектора от полученной точки на сцене до центра сферы.

Полученное значение длины вектора и будет искомым радиусом сферы.

На момент реализации нам не удалось найти способ определения размера объекта на сцене, и мы решили сделать отрисовку метки финиша с помощью UIKit. Алгоритм в этом случае повторяет шаги 1-5, после чего на экране рисуется окружность нужного размера с центром в точке, полученной в шаге 2 средствами UIKit. Пример реализации метки с использованием UIKit можно найти здесь.

Различие использования SceneKit и UIKit в данном случае заключается еще и в том, что при реализации на SceneKit объект SCNNode для конечной точки маршрута (метки финиша) будет создан с материалом и геометрией, так как он должeн быть видимым, в то время как при использовании UIKit объект нода нам понадобится исключительно для поиска проекции на плоскость экрана (для определения цетра метки на экране). Геометрию и материал в этом случае добавлять не нужно. Заметим, что расстояние от камеры до объекта SCNNode конечной точки маршрута можно найти двумя способами – используя географические координаты точек, либо как длину вектора между точками на сцене. Это возможно благодаря тому, что объект камеры является свойством SCNNode. Для получения нода камеры необходимо обратиться к свойству pointOfView нашей сцены.

Мы научились определять радиус нода метки финиша в произвольный момент времени при реализации на SceneKit и положение вьюхи метки финиша в случае реализации на UIKit. Остается понять, когда необходимо обновлять эти значения? Таким местом является метод объекта SCNSceneRendererDelegate:

renderer(_ renderer: SCNSceneRenderer, didRenderScene scene: SCNScene, atTime time: TimeInterval)

Этот метод вызывается после каждого отрендеренного кадра сцены. Обновляя значения свойств в теле этого метода, мы получим корректно отображенную метку финиша.

Анимация

После того, как метка финиша появилась в dev’е, мы приступили к добавлению анимации пульсации к этой метке. Думаю, для большинства iOS разработчиков создание анимаций не представляет особых проблем. Но при обдумывании способа реализации мы столкнулись с проблемой постоянного обновления frame'а нашей вьюхи. Отмечу, что в большинстве случаев анимации добавляются к статическим объектам UIView. Аналогичная проблема – постоянное обновление радиуса геометрии нода возникает и при реализации с помощью SceneKit. Дело в том, что пульсирующая анимация сводится к анимации размера окружности (для UIKit) и радиуса сферы (для SceneKit). Да-да, мы знаем что в UIKit такую анимацию можно сделать, используя CALayer, но для простоты повествования я решил рассмотреть этот вопрос симметрично для двух фреймворков. Рассмотрим реализацию на UIKit. Если добавить к существующему коду, обновляющему фрейм вьюхи код, анимирующий этот же фрейм, то анимация будет сбиваться явной установкой фрейма. Поэтому в качестве решения данной проблемы мы решили использовать анимацию свойства transform.scale.xy объекта UIView. При реализации с использование SceneKit придется добавить анимацию свойства scale для объекта SCNNode. Приятным моментом использования SceneKit в данном случае является тот факт, что он полностью поддерживает CoreAnimation, поэтому учить новое API не обязательно. Код, реализующий анимацию схожую с анимацией метки в Яндекс.Картах, выглядит примерно так:

let animationGroup = CAAnimationGroup.init()
animationGroup.duration = 1.0
animationGroup.repeatCount = .infinity

let opacityAnimation = CABasicAnimation(keyPath: "opacity")
opacityAnimation.fromValue = NSNumber(value: 1.0)
opacityAnimation.toValue = NSNumber(value: 0.1)

let scaleAnimation = CABasicAnimation(keyPath: "scale")
scaleAnimation.fromValue = NSValue(scnVector3: SCNVector3(1.0, 1.0, 1.0))
scaleAnimation.toValue = NSValue(scnVector3: SCNVector3(1.2, 1.2, 1.2))

animationGroup.animations = [opacityAnimation, scaleAnimation]
finishNode.addAnimation(animationGroup, forKey: "animations")

Билборд

В начале статьи я упоминал про билборд с расстоянием до конечной точки маршрута, который, по сути, представляет собой лейбл с текстом, расположенный всегда над меткой финиша. По традиции я обозначу проблемы свойственные реализациям на UIKit и SceneKit, рассказав о возможных решениях для каждого из фреймворков.

Начнем с UIKit. В данном случае билборд представляет собой обычный UILabel, в котором постоянно обновляется текст, показывающий расстояние до конечной точки маршрута. Посмотрим на проблему, с которой мы столкнулись.

Если задать лейблу какой-нибудь фрейм, а затем повернуть телефон, мы увидим, что фрейм не изменится (было бы странно, если бы это было не так). В то же время нам хотелось бы, чтобы лейбл оставался параллельным плоскости земли.

Думаю, всем понятно, что при изменении ориентации девайса нам необходимо повернуть лейбл, но на какой угол? Если включить воображение и представить мысленно все оси систем координат и вектора, участвующие в данном процессе, можно прийти к выводу, что угол поворота равен углу между осью x системы координат UIKit и проекцией оси X системы координат SceneKit на плоскость экрана.

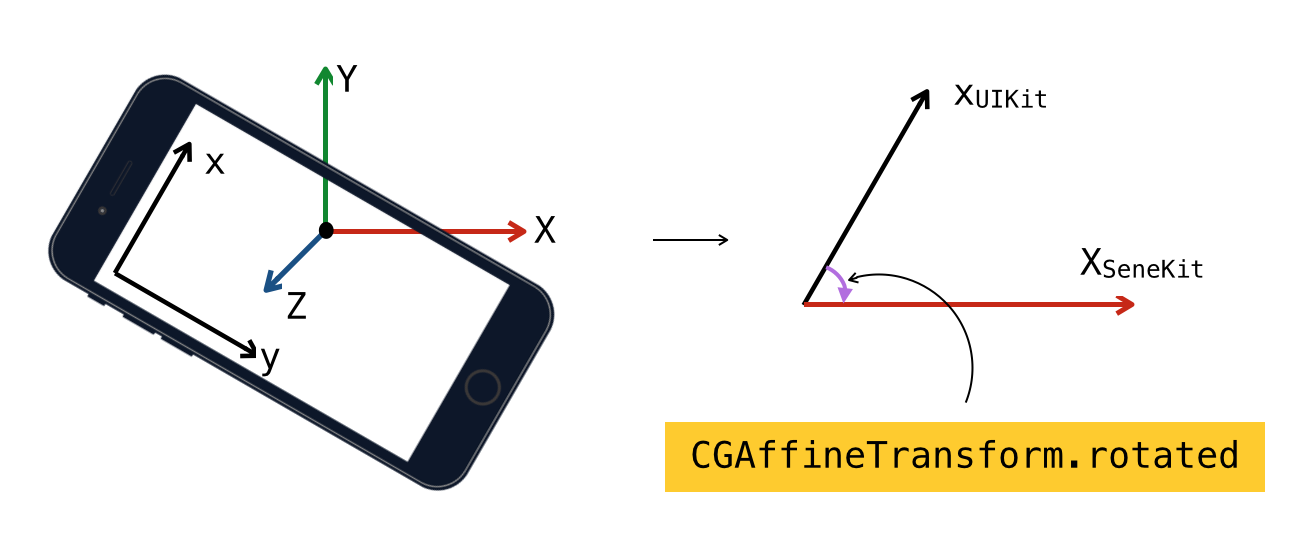
Простая задача, которая в очередной раз доказала пользу школьного курса геометрии.

При реализации метки финиша с использованием SceneKit рендерить билборд с расстоянием вам, скорее всего, придется так же средствами SceneKit, а значит, перед вами определенно возникнет задача заставить объект SCNNode всегда быть ориентированным к камере. Думаю, проблема станет более понятной, если взглянуть на картинку:

Решается эта задача путем использования SCNBillboardConstraint API. Добавив констрейнт со свободной осью Y в коллекцию констрейнтов нашего нода, мы получим нод, который вращается вокруг оси Y своей системы координат, таким образом, чтобы всегда быть ориентированным к камере. Единственной задачей разработчика становится разместить этот нод на правильной высоте, чтобы билборд с расстоянием всегда был виден пользователю.

let billboardConstraint = SCNBillboardConstraint()
billboardConstraint.freeAxes = SCNBillboardAxis.Y
finishNode.constraints = [billboardConstraint]

Вспомогательная метка

Одной из главных фич пешеходной маршрутизации с дополненной реальностью мы внутри команды считаем вспомогательную метку – специальный визуальный элемент, который появляется на экране в тот момент, когда конечная точка маршрута уходит из зоны видимости и показывает пользователю, куда необходимо повернуть телефон, чтобы на экране появилась метка финиша.

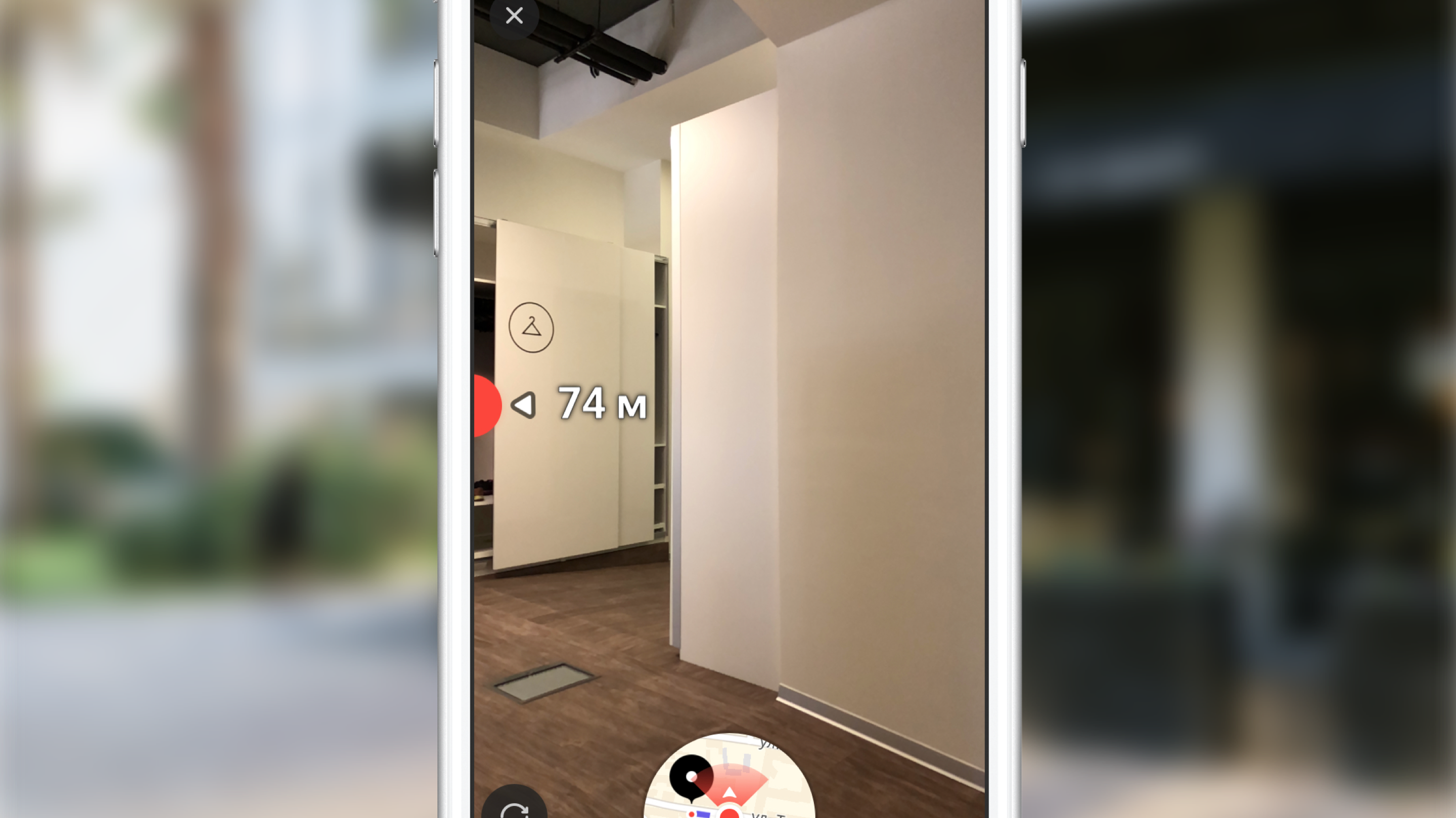
Уверен, многие из читателей встречали подобную функциональность в некоторых играх, чаще всего – шутерах. Какого же было удивление нашей команды, когда мы увидели этот элемент UI в макетах. Сразу скажу, что корректная реализация такой фичи может потребовать от вас не один час экспериментов, но конечный результат стоит потраченного времени. Мы начали с определения требований, а именно:

• при любой ориентации девайса, метка двигается вдоль границ экрана,
• если пользователь повернулся на 180 градусов к конечной точке маршрута, метка отображается у нижний границы экрана,
• в каждый момент времени поворот в сторону метки должен быть кратчайшим поворотом к конечной точке маршрута.

После описания требований мы приступили к реализации. Практически сразу мы пришли к выводу, что рендеринг будет осуществлен с использованием UIKit. Основной проблемой при реализации стало определение центра этой метки в каждый момент времени. После рассмотрения метки финиша, подобная задача не должна вызвать затруднений, поэтому я не буду подробно останавливаться на ее решении. В статье я приведу лишь описание алгоритма выбора центра вспомогательной метки, а исходный код можно посмотреть тут.

Алгоритм поиска центра вспомогательной метки:

1. создать для конечной точки маршрута объект SCNNode с позицией на сцене, полученной из географической координаты точки,
2. найти проекцию точки на плоскость экрана,
3. найти пересечение отрезка из центра экрана до точки найденной проекции с отрезками границ экрана в системе координат экрана.

Найденная точка пересечения является искомым центром вспомогательной метки. По аналогии с кодом, обновляющим параметры метки финиша, код, отрисовывающий вспомогательную метку, мы поместили в уже озвученный выше метод делегата.

Полилиния маршрута

Построив маршрут и увидев на экране метку финиша, пользователь может дойти до нее ориентируясь только по направлению до метки, но маршрутизация потому так и называется, что показывает пользователю маршрут. Мы подумали, что было бы очень странно урезать функциональность пешеходной маршрутизации, исключив из AR версии отображения маршрута. Для визуализации линии маршрута было решено отображать набор стрелок, двигающихся вдоль нее. В данном случае дизайнеров устраивало, что стрелки при отдалении будут практически исчезать (размер будет определяться правилами перспективной проекции), и было решено использовать для реализации SceneKit.

Прежде чем приступить к описанию реализации, важно отметить, что по дизайну, стрелки дожны были находиться на расстоянии 3 м друг от друга. Если оценить количество объектов (стрелок) которое необходимо отрендерить при маршруте длиной около 1 км то оно составит примерно 330 шт. При этом, каждому объекту добавляется анимация движения вдоль своего участка маршрута. Отметим, что стрелки, удаленные от положения камеры на сцене на расстояние порядка 100-150 метров практически не видны из за небольшого размера. Рассмотрев эти факторы было решено не отображать все объекты, а отображать лишь те из них, которые удалены от пользователя не более чем на 100 метров вдоль линии маршрута, периодически обновляя отображаемый набор объектов. Мы отображаем достаточный объем визуальной информации, исключая ненужные вычисления SceneKit и экономя батарейку пользователя.

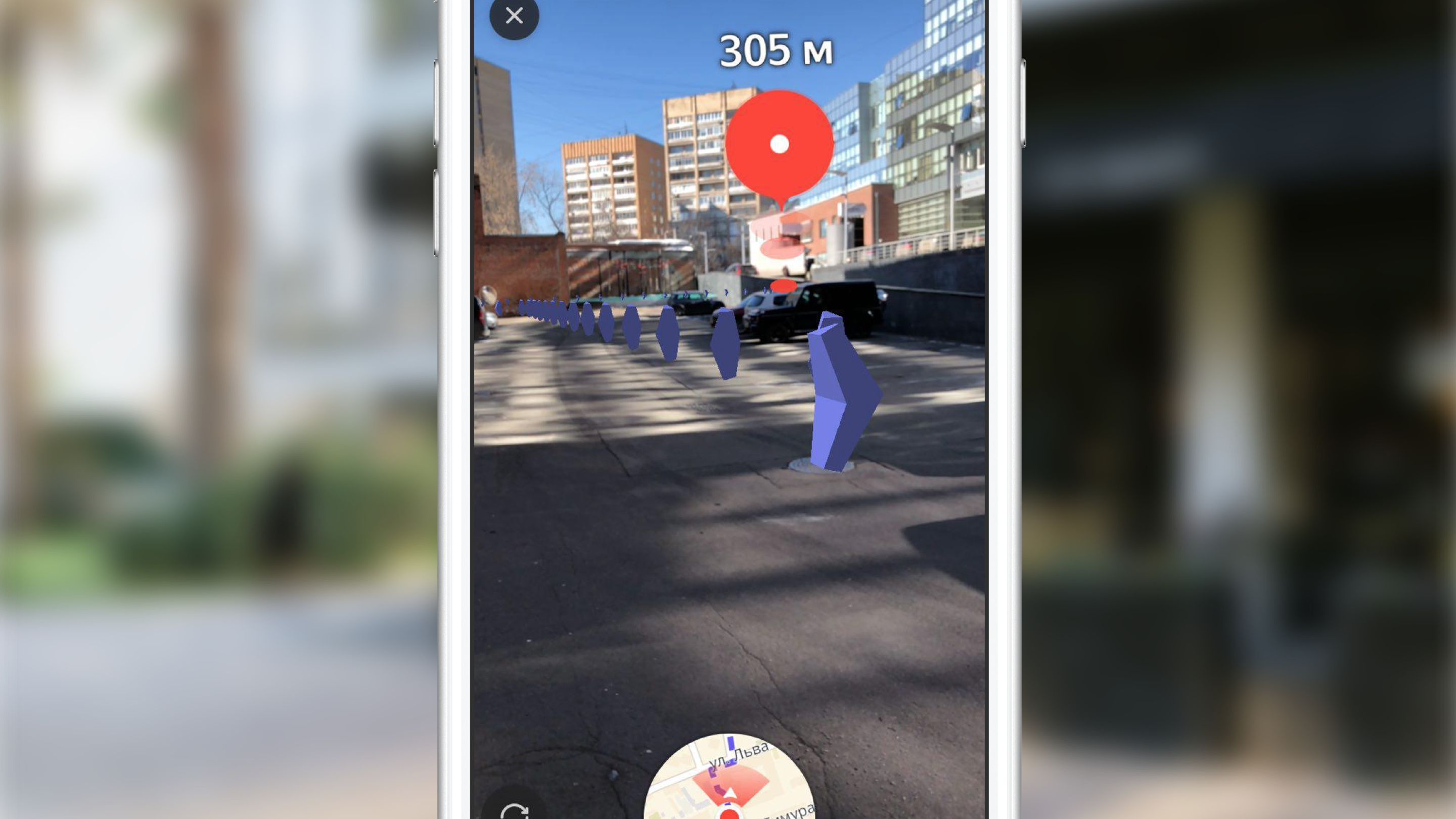
Давайте рассмотрим основные шаги, которые нам предстояло воплотить в жизнь для получения конечного результата:

• выбор участка маршрута, для которого будем отображать примитивы,
• создание 3D моделей,
• создание анимации,
• обновление при движении по маршруту.

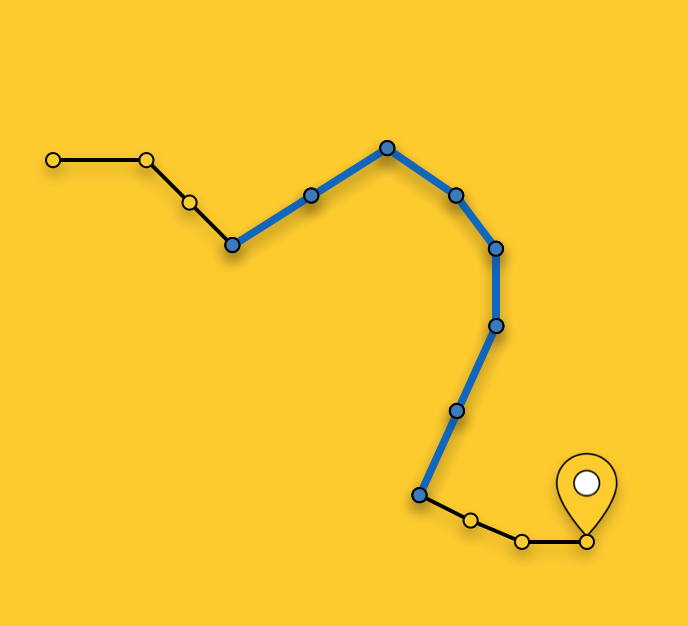
Выбор участка для отображения

Как я уже отмечал выше, мы не отображаем стрелки для всего маршрута, а выбираем оптимальный для отображения участок. Выбор участка в произвольный момент времени заключается в поиске ближайшего сегмента маршрута (маршрут является последовательностью сегментов/отрезков) к текущей позиции пользователя и выборе сегментов от ближайшего в сторону конечной точки маршрута до тех пор, пока их суммарная длина не превысит 100 метров.

Создание 3D модели

Рассмотрим более подробно процесс создания 3D модели. В большинстве случаев всё, что вам необходимо сделать для создания простой 3D модели (как наша стрелка), это открыть любой 3D редактор, потратить некоторое время на его освоение и сделать в нем эту модель. В случае, если ребята из вашей команды обладают опытом 3D моделирования, или у них есть время учить, к примеру, 3DMax (и он должен быть куплен), то вам несказанно повезло. К сожалению, на момент реализации этой фичи, особым опытом никто из нас не обладал, свободного времени на обучение не было, поэтому нам пришлось делать модель, так сказать, подручными средствами. Я имею ввиду описание модели в коде. Началось все с представления 3D-модели в виде треугольников. Затем нам пришлось вручную найти координаты вершин этих треугольников в системе координат модели, после чего создать массив индексов вершин треугольников. Имея в распоряжении эти данные, мы можем создать необходимую геометрию прямо в SceneKit. Создать модель, подобную нашей можно, например, так:

class ARSCNArrowGeometry: SCNGeometry {
    convenience init(material: SCNMaterial) {
        let vertices: [SCNVector3] = [
            SCNVector3Make(-0.02,  0.00,  0.00), // 0
            SCNVector3Make(-0.02,  0.50, -0.33), // 1
            SCNVector3Make(-0.10,  0.44, -0.50), // 2
            SCNVector3Make(-0.22,  0.00, -0.39), // 3
            SCNVector3Make(-0.10, -0.44, -0.50), // 4
            SCNVector3Make(-0.02, -0.50, -0.33), // 5
            SCNVector3Make( 0.02,  0.00,  0.00), // 6
            SCNVector3Make( 0.02,  0.50, -0.33), // 7
            SCNVector3Make( 0.10,  0.44, -0.50), // 8
            SCNVector3Make( 0.22,  0.00, -0.39), // 9
            SCNVector3Make( 0.10, -0.44, -0.50), // 10
            SCNVector3Make( 0.02, -0.50, -0.33), // 11
        ]
        let sources: [SCNGeometrySource] = [SCNGeometrySource(vertices: vertices)]
        let indices: [Int32] = [0,3,5, 3,4,5, 1,2,3, 0,1,3, 10,9,11, 6,11,9, 6,9,7, 9,8,7,
                                6,5,11, 6,0,5, 6,1,0, 6,7,1, 11,5,4, 11,4,10, 9,4,3, 9,10,4, 9,3,2, 9,2,8, 8,2,1, 8,1,7]
        let geometryElements = [SCNGeometryElement(indices: indices, primitiveType: .triangles)]
        self.init(sources: sources, elements: geometryElements)
        self.materials = [material]
    }
}

static func arrowBlue() -> SCNGeometry {
    let material = SCNMaterial()
    material.diffuse.contents = UIColor.blue
    material.lightingModel = .constant
    return ARSCNArrowGeometry(material: material)
}

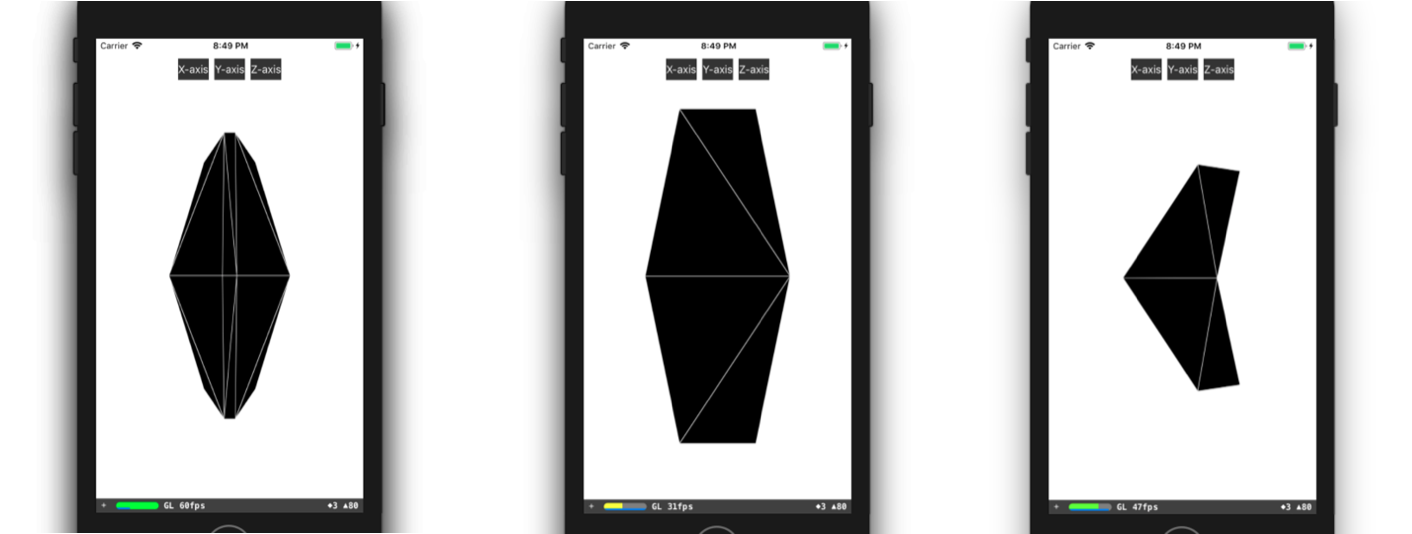
Итоговый результат выглядит так:

Анимация линии маршрута

Следующим этапом на пути к отображению анимированной линии маршрута стал этап создания непосредственно анимации. Но каким способ реализовать анимацию, которая в конечном виде выглядит так, будто стрелка начинает свое движение в начальной точке выбранного участка маршрута и «плывет» вдоль маршрута до конца этого участка?

Я не буду описывать все возможные способы создания подобной анимации, вместо этого более подробно остановлюсь на том способе, который выбрали мы. После того, как участок маршрута выбран, мы делим его на участки одинаковой длины – участки анимации одной стрелки. Каждый такой участок выделен своим цветом и имеет длину равную расстоянию между стрелками.

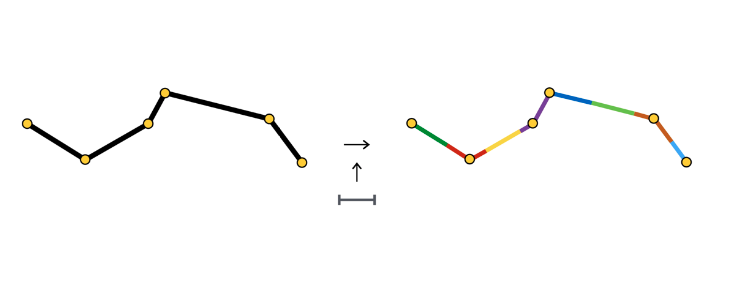
В начале каждого участка мы создаем объект SCNNode стрелки, анимация которого заключается в движении вдоль своего участка.

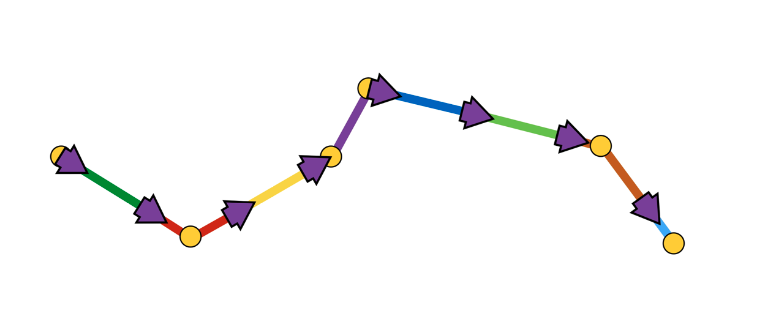
Как видно, участок анимации иногда состоит из одного сегмента, иногда из двух и более. Всё зависит от шага (в нашем случае – 3 метра) между стрелками и координатами точек, которые составляют маршрут.

Анимация стрелки представляет собой последовательность из двух шагов:

• появление в начальной позиции с начальным углом поворота,
• последовательность смещений вдоль сегментов с поворотами в точках соединения сегментов.

Схематично это выглядит так:

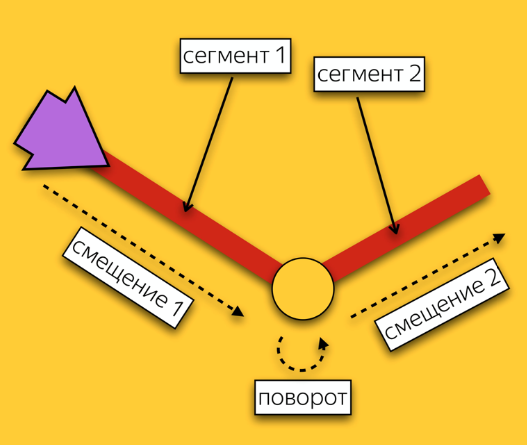
Реализовывать подобную анимацию нам показалось проще всего с помощью SCNAction API – декларативное API, позволяющее удобно создавать последовательные, групповые и повторяющиеся анимации. Подробнее посмотреть на реализацию можно тут. Благодаря тому, что каждая стрелка заканчивает свою анимацию в стартовой точке участка анимации следующей стрелки, создается впечатление непрерывного движения стрелки вдоль всего выбранного участка маршрута.

На этом предлагаю закончить рассмотрение различных аспектов рендеринга и перейти к основной части – определение позиций объектов на сцене по географическим координатам объектов.

Определение позиции объекта на сцене

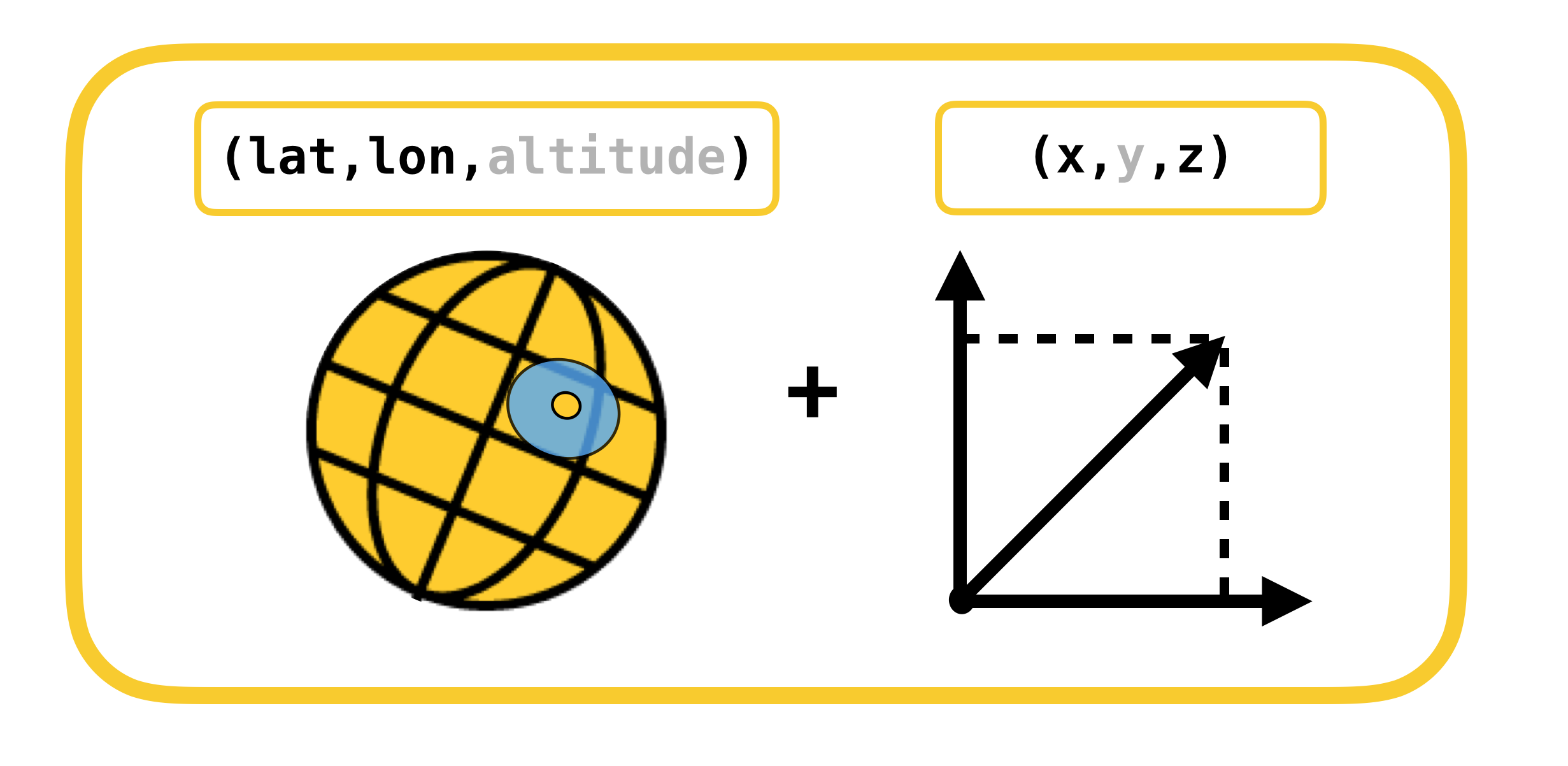
Начнем разговор об определении позиции объекта на сцене с рассмотрения систем координат, конвертацию между которыми необходимо осуществить. Их всего 2:

• геодезические (или географические для простоты) координаты – положение объектов (точек маршрута) в реальном мире,
• декартовы координаты – положение объектов на сцене (в ARKit). Вспомним, что система координат сцены совпадает с системой координат ARKit (в случае использования ARSCNView).

Перевод из одной системы координат в другую и обратно возможен благодаря тому, что координаты в ARKit измеряются в метрах, а смещение между двумя геодезическими координатами можно с большой точностью перевести в смещение в метрах по осям X и Z системы координат ARKit при небольших смещениях. Напомню, что геодезические координаты – это точки с определенной долготой и широтой.

Давайте вспомним такие важные понятия из курса географии, как параллели и меридианы, и их основные свойства:

• Параллель – линия с градусным значением широты. Длины различных параллелей различны.
• Меридиан – линия с градусным значением долготы. Длины всех меридианов одинаковы.

Теперь посмотрим, как можно рассчитать смещение в метрах, между двумя геодезическими координатами с координатами и :

,

,

Теперь, когда мы умеем переводить смещение из одной системы координат в другую, нужно определиться с точкой начала отсчета – точка, для которой одновременно известны географическая координата и координата в ARKit (координата на сцене). Найдя такую точку, мы сможем определить координату любого объекта на сцене, зная его географическую координату и используя вышеприведенные формулы.

Для большей ясности рассмотрим пример:
В момент начала сессии дополненной реальности мы запросили у CoreLocation нашу географическую координату и получили её моментально — . Вспомнив тот факт, что начало системы координат ARKit находится в момент старта сессии в точке, где расположено устройство, мы получили точку начала отсчета, так как нам известна географическая координата и координата на сцене . Пусть нам необходимо найти координату на сцене объекта с географической координатой . Для этого найдем смещение в метрах между географической координатой объекта и географической координатой нашей точки начала отсчета, а затем найденное смещение прибавим к координате на сцене точки начала отсчета. Полученная координата на сцене и будем являться искомой.

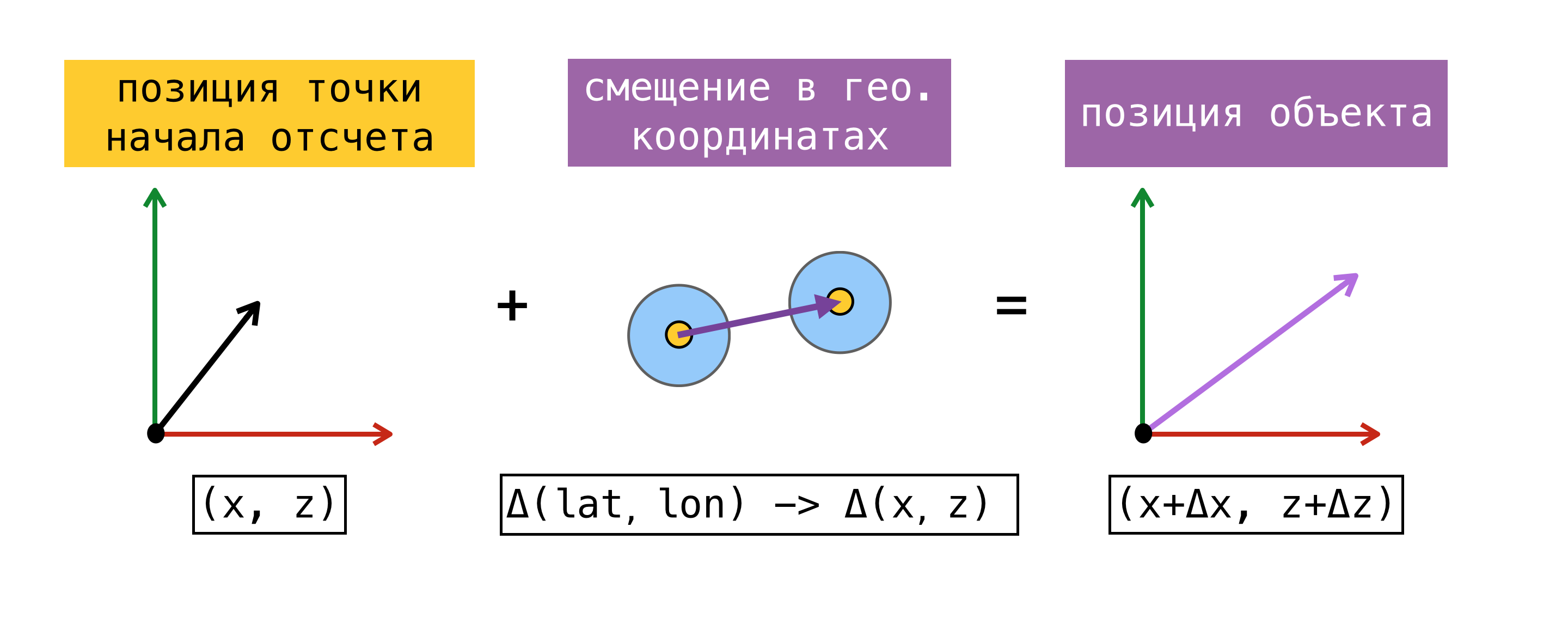
Отмечу, что найденная таким способом позиция на сцене будет соответствовать положению объекта в реальном мире только в том случае, если оси X/Z системы координат сцены сонаправлены с направлениям на Юг/Восток. Сонаправленность осей, по идее, должна достигаться за счет установки флага worldAlignment в значение gravitiAndHeading. Но как я уже говорил в начале поста, это далеко не всегда так.

Рассмотрим более подробно способ определения точки начала отсчета. Для этого введем понятие эстимейт – совокупность географической координаты и координаты на сцене.

Предложенный выше способ определения точки начала отсчета может быть использован не всегда. В момент старта сессии дополненной реальности, запрос на получение CLLocation пользователя может быть выполнен не моментально, более того, точность полученной координаты может обладать большой погрешностью. Более правильным будет запросить у SceneKit позицию на сцене в тот момент, когда мы получаем значение от CoreLocation. В этом случае компоненты полученного эстимейта действительно получены одновременно, и у нас появляется возможность использовать любой из эстимейтов, как точку начала отсчета. При работе с ARKit погрешность в смещении со временем накапливается, поэтому Apple не рекомендует использовать ARKit как инструмент для навигации.

Когда мы решили реализовать пешеходную маршрутизацию с дополненной реальностью, мы провели небольшое исследование существовавших на тот момент решений, использующий ARKit для похожих задач, и натолкнулись на фреймворк ARKit+CoreLocation. Идея этого фреймворка заключалась в том, что благодаря ARKit мы можем более точно определить местоположение пользователя, чем при использовании исключительно CoreLocation.

Концепция ARKit+CoreLocation:

• при получении CLLocation от CLLocationManager
  • запрашиваем позицию на сцене, используя scene.pointOfView.worldPosition
  • сохраняем эту пару координат (эстимейт) в буфер
• при необходимости получить точное местоположение
  • выбираем лучший эстимейт
  • рассчитываем смещение между текущей позицией на сцене и позицией на сцене лучшего эстимейта
  • применяем найденное смещение к географической координате лучшего эстимейта

Рассчитанная с использованием лучшего эстимейта географическая координата пользователя будет точнее, чем последнее значение, полученное от CoreLocation, и при этом будет обладать меньшей погрешностью.

Осталось лишь понять, что значит «лучший эстимейт». Для этого посмотрим, как он выбирается и когда обновляется.

Алгоритм выбора лучшего эстимейта (выбирается, используя только географическую компоненту):

• лучший по точности (обладающий наименьшим horizontalAccuracy),
• самый новый среди эстимейтов с одинаковой точностью,
• выбирается среди эстимейтов на расстоянии не более 100 метров от текущего местоположения.

Алгоритм выбора обновляет лучший эстимейт при каждом апдейте от CoreLocation и по таймеру. Обновление по таймеру необходимо, так как пользователь может двигаться, при этом данные от CoreLocation могут не приходить, а в алгоритме выбора должны участвовать только эстимейты на расстоянии не более 100 метров от текущего местоположения.

В нашей реализации мы используем лучший эстимейт, как точку начала отсчета при нахождении позиций точек маршрута на сцене. Напомню, что мы периодически обновляем всю конфигурацию объектов сцены при движении пользователя по маршруту, так как мы отображаем только часть маршрута (около 100 метров).

Корректировка системы координат

Выше я уже упоминал о проблеме того, что оси X/Z системы координат ARKit не всегда сонаправлены с реальными направлениями на Восток/Юг при старте сессии. ARKit инициализирует систему координат единожды, после чего не пытается скорректировать направления осей, так как в большинстве применений дополненной реальности направление осей не играет роли.

Но для навигационных приложений, крайне важным является именно конвертация географических координат в координаты сцены. Если оси будут направлены как написано в документации, и конвертацию сделать без ошибок, то пользователь увидит на экране телефона помещенные на сцену объекты именно там, где они и должны быть в реальном мире. В противном случае объекты будут смещены на некоторый угол. Самой сложной задачей в пешеходной маршрутизации с AR безусловно является задача корректировки осей. Я постараюсь описать алгоритм ее решения максимально полно, а проверить, что у нас получилось, вы всегда сможете, скачав Яндекс.Карты и запустив пешеходную маршрутизацию в режиме AR.

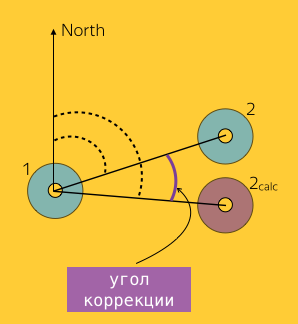
Определение угла коррекции

Рассмотрим на конкретном примере, что же это за угол коррекции. Представим себе, что в момент времени мы получили от CLLocationManager местоположение пользователя и запросили положение на сцене — . Аналогично в момент времени имеем еще одно показание от CLLocationManager — и позицию на сцене соответственно.

Рассчитанная с помощью смещения в ARKit — географическая координата эстимейта 2 должна совпадать с показанием CoreLocation в момент времени . Таким образом должна быть равна . Это будет верное с большой точностью, если погрешность показания CoreLocation равна нулю и оси двух систем координат соноправлены. В реальном мире эти значения отличаются. Это обусловлено наличием угла поворота системы координат ARKit относительно реальных направлений на Восток/Юг.

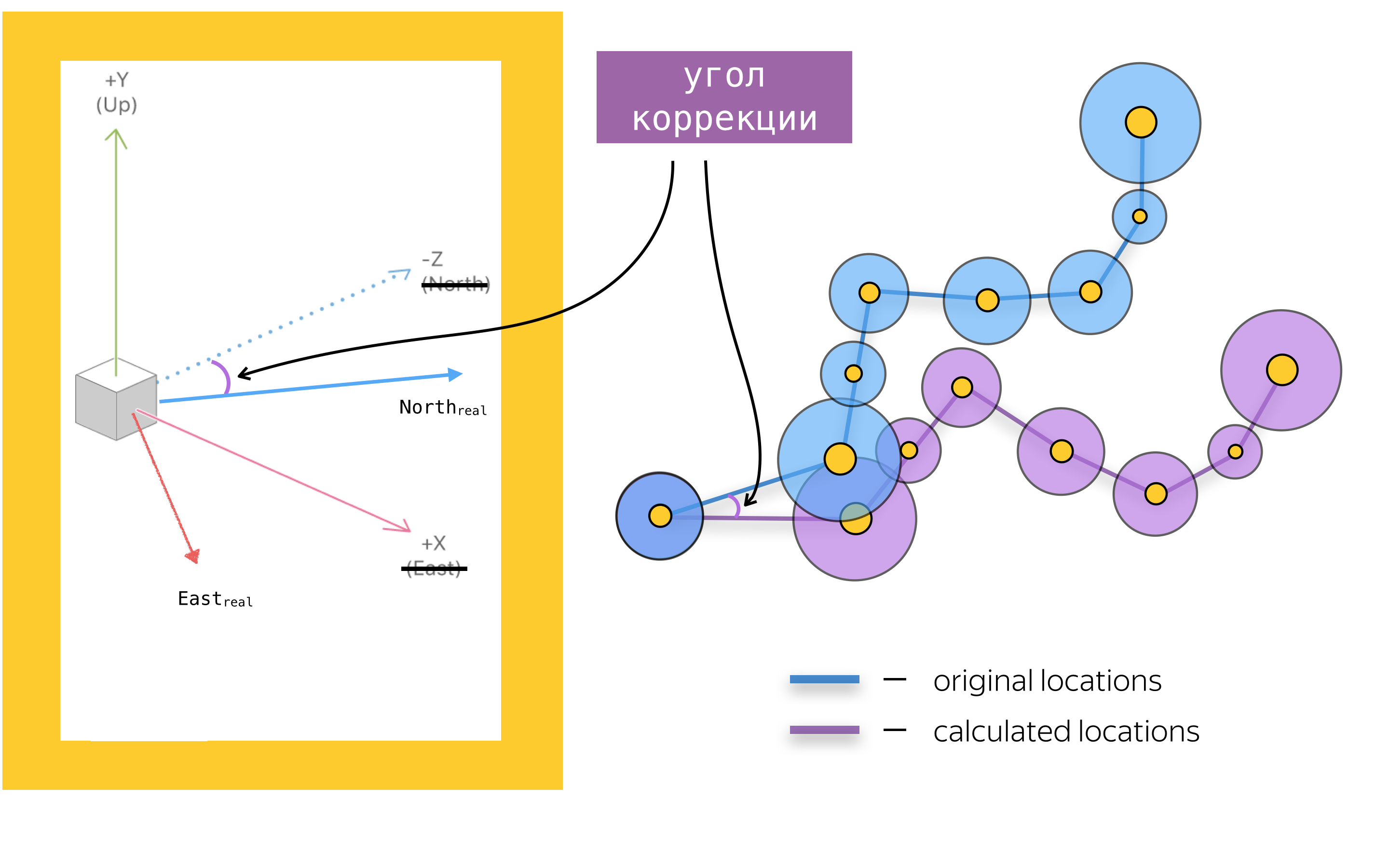
Как же найти этот угол и повернуть систему координат ARKit на этот угол относительно оси Y? Приведу наш алгоритм и постараюсь подробно объяснить каждый из шагов. В общих чертах алгоритм включает в себя следующие шаги:

1. буфферизация эстимейтов по времени или количеству,
2. фильтрация эстимейтов,
3. выбор пар эстимейтов для усреднения,
4. расчет угла корректировки для каждой из выбранных пар,
5. усреднение по всем выбранным парам.

Начнем с буфферизации. Здесь ничего сложного. Поступающие от CLLocationManager'а данные накапливались в буфер, который оповещал о необходимости произвести рассчет по достижению либо опреденного количества элементов в буфере (предел по количеству), либо по завершению некоторого промежутка времени (предел по времени).

Вычисление угла корректировки для пары эстимейтов 1, 2 заключается в вычислении разности между двумя углами: и , где – географическая координата эсимейта 2, рассчитанная с использованием смещения в ARKit. Как вычислять можно посмотреть тут (в разделе Bearing).

Фильтрация эстимейтов заключается в исключении эстимейтов с плохой точностью и находящихся на слишком близком расстоянии друг от друга. Почему мы исключаем эситмейты, если они находятся слишком близко друг к другу? Понимая, как мы считаем угол коррекции для пары эстимейтов, можно рассмотреть, чему равна погрешность измерения этого угла в случае, когда эстимейты находятся далеко и близко друг к другу. Так как географическая координата обладает сама по себе некоторой точностью, логично изобразить географическую координату не точкой, а окружностью с радиусом, равным значению horizontalAccuracy. Угол коррекции, который мы вычисляем, рассчитывается на основании углов между направлением на Север и отрезком, соединяющим центры окружностей. Так как пользователь на самом деле может находится в любой точке этих окружностей погрешность определения угла коррекции можно изобразить так:

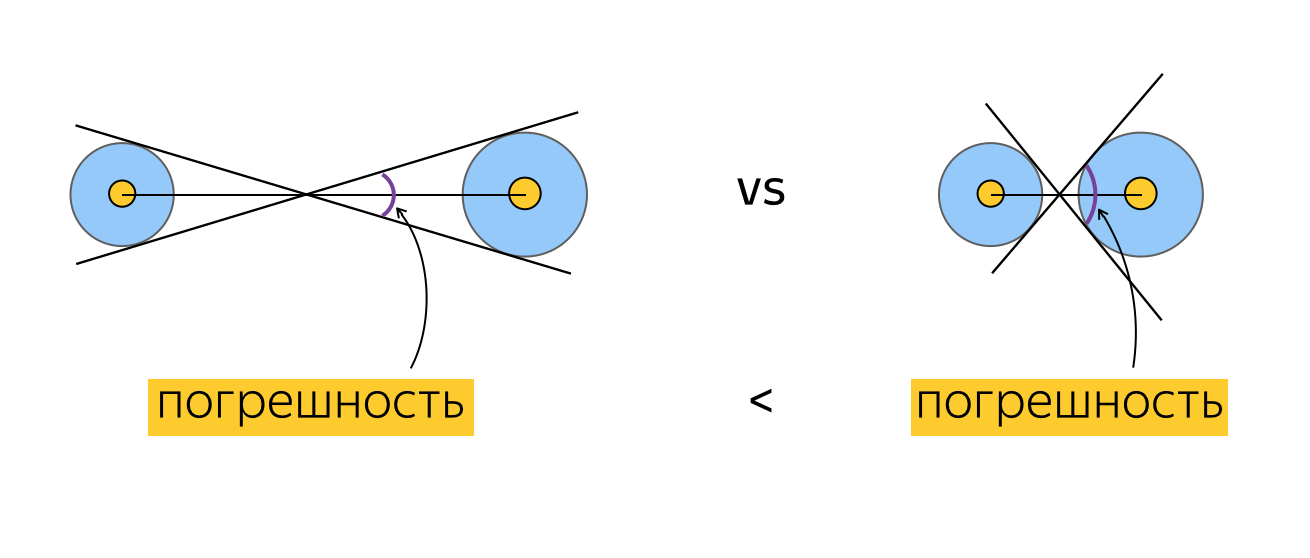
Эта схема, на мой взгляд, достаточно наглядно доказывает утверждение о более высокой точности определения угла коррекции при расчете для более удаленных эстимейтов.

Поговорим о выборе пар. Очевидно, что существует много способов выбрать пары из произвольного набора элементов. Например:

• случайный N процентов от всех возможных пар,
• каждый элемент участвует только в одной паре,
• M процентов пар с наибольшим весом (что такое вес?).

В ситуации, когда выбор пар необходим, как в нашем случае, для расчета некоторой величины, было решено попробовать ввести некоторую величину (вес), характеризующую конкретную пару и использовать только пары с наибольшим весом для более точного расчета. В качестве веса пары было выбрано отношение расстояния между географическими координатами эстимейтов к сумме радиусов окружностей, описанных выше. Как я уже показал, чем больше расстояние между эстимейтами, тем меньше погрешность определения угла коррекции для пары из этих эстимейтов. Не сложно понять, что погрешность тем ниже, чем меньше радиусы окружностей (выше точность каждой из координат). Таким образом вес пары растет при отдалении эстимейтов и более высокой точности каждой из координат.

К сожалению, сравнив различные способы выбора пар мы не заметили выигрыша при использовании пар с более высоким весом. Возможно, это обусловлено небольшим количеством эстимейтов, используемых для расчета угла коррекции (так как для накопления большого числа эстимейтов необходимо большое количество времени, а пользователь хочет как можно скорее увидеть объекты на сцене там, где они и должны быть).

Тестирование

Разумеется, написать алгоритм это лишь часть работы. Для того, чтобы выпускать решение в продакшн, нам необходимо было определить, насколько хорошо работает наше решение. Сделать это можно ответив на 2 вопроса:

• насколько точно рассчитывается угол коррекции,
• достаточно ли хорошо алгоритм работает в реальных условиях.

Про юнит-тесты на определение точности расчета угла я, пожалуй, писать не буду, так как они ничем не примечательны, а вот про работу в реальных условиях расскажу поподробнее.

За время одной сессии пешеходной маршрутизации алгоритм по корректировке направления осей можно применить разное колличество раз. Мы можем, например, накопить 100 показаний CLLocation, произвести расчет угла коррекции и больше никогда этого не делать. С другой стороны, мы можем применять наш алгоритм, скажем, каждые 10 секунд (за это время мы получим в среднем 10 показаний). Как же выбрать один из способ и при этом подобрать оптимальные параметры? Как и все задачи в процессе разработки ПО, эту задачу можно решить с разной степенью "серьезности". Думаю все согласятся, что наш эвристический алгоритм очень чувствителен к данным. Можно достаточно точно сказать, что чем больше данных попадет ему на вход, и чем при этом точнее они будут, тем точнее будет результат. Проблема в том, что мы заранее не можем даже сказать, нужно ли вообще корректировать оси. Тем более мы не можем оценить, насколько точным будут следующие показания CoreLocation. Именно поэтому алгоритм работает периодически, срабатывая на каждое оповещение буфера. Остается проверить, что алгоритм в реальных условиях сходится.

Поясню понятие сходимости алгоритма в данном контексте. Сходимостью алгоритма мы называем состояние, в котором каждое следующее срабатывание приводит ко всё более малому углу коррекции. В конечном счете, если запускать алгоритм непрерывно (напомню, что для срабатывания ему необходимо накопить данные), то через некоторое время он должен практически не корректировать оси, колеблясь вблизи значения угла коррекции равного 0 градусов. Очевидно, что чем данные хуже, тем больше амплитуда колебаний.

Оценку сходимости мы проверяли в ходе "полевых испытания". Мы строили различные маршруты в окрестностях офиса и по дороге из дома на работу. Во время этих прогулок мы оценивали, то насколько точно алгоритму удается скорректировать направление осей, а также логировали различные данные, такие как позицию пользователя в реальном мире, позицию на сцене в момент получения очередного CLLocation, выбранные пары эстимейтов для каждого расчета угла коррекции, рассчитанный угол для каждой из пар и усредненное значение по всем парам. Эти данные позволяли нам проверять разные гипотезы (например какой способ выбора пар лучше работает на реальных данных) и найти причины сбоев в работе алгоритма.

Для примера приведу ситуацию, когда сессия дополненной реальности была проинициализирована с некорректным направлением осей ARKit.

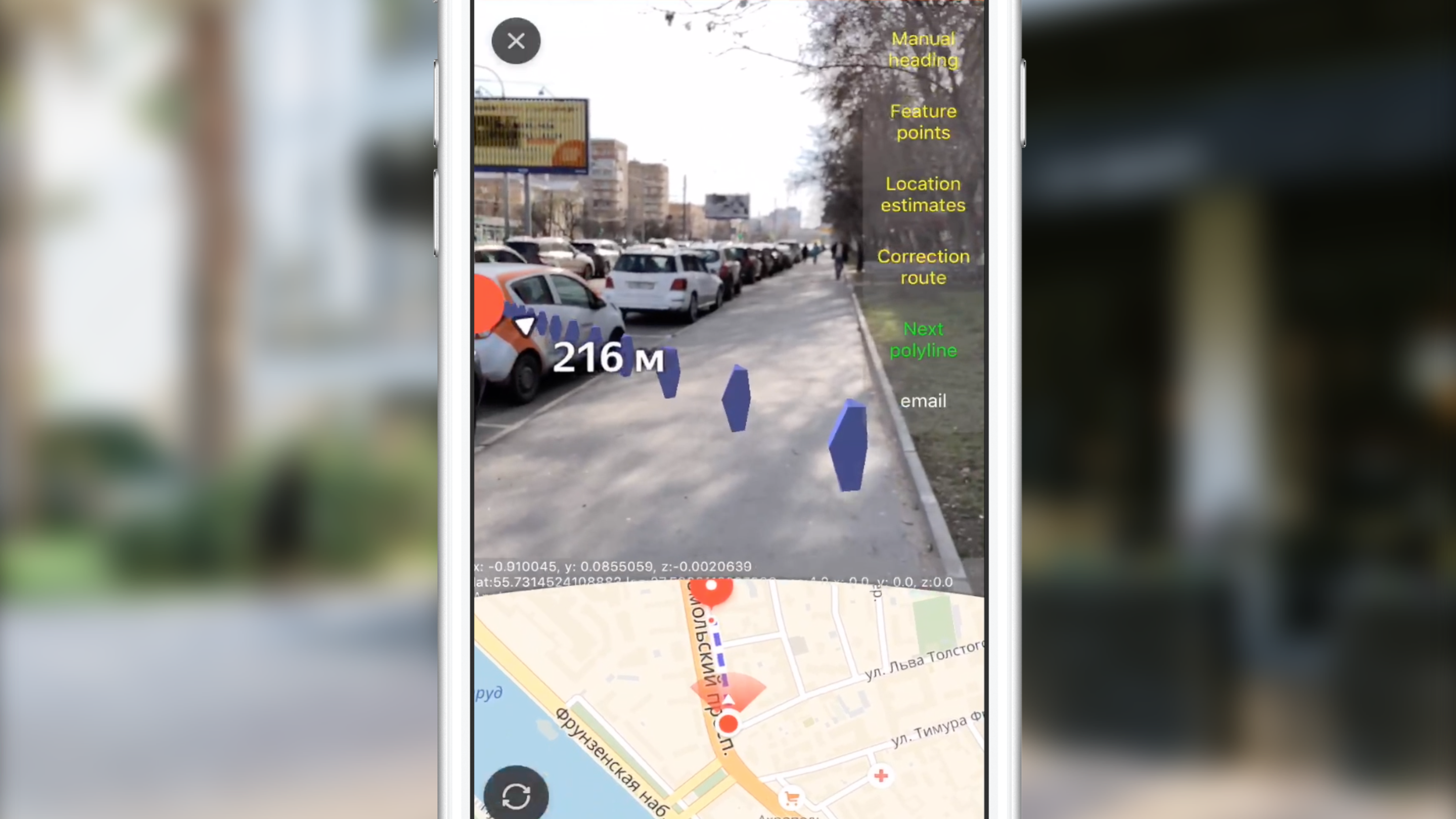
Видно, как картина меняется после первого срабатывания алгоритма.

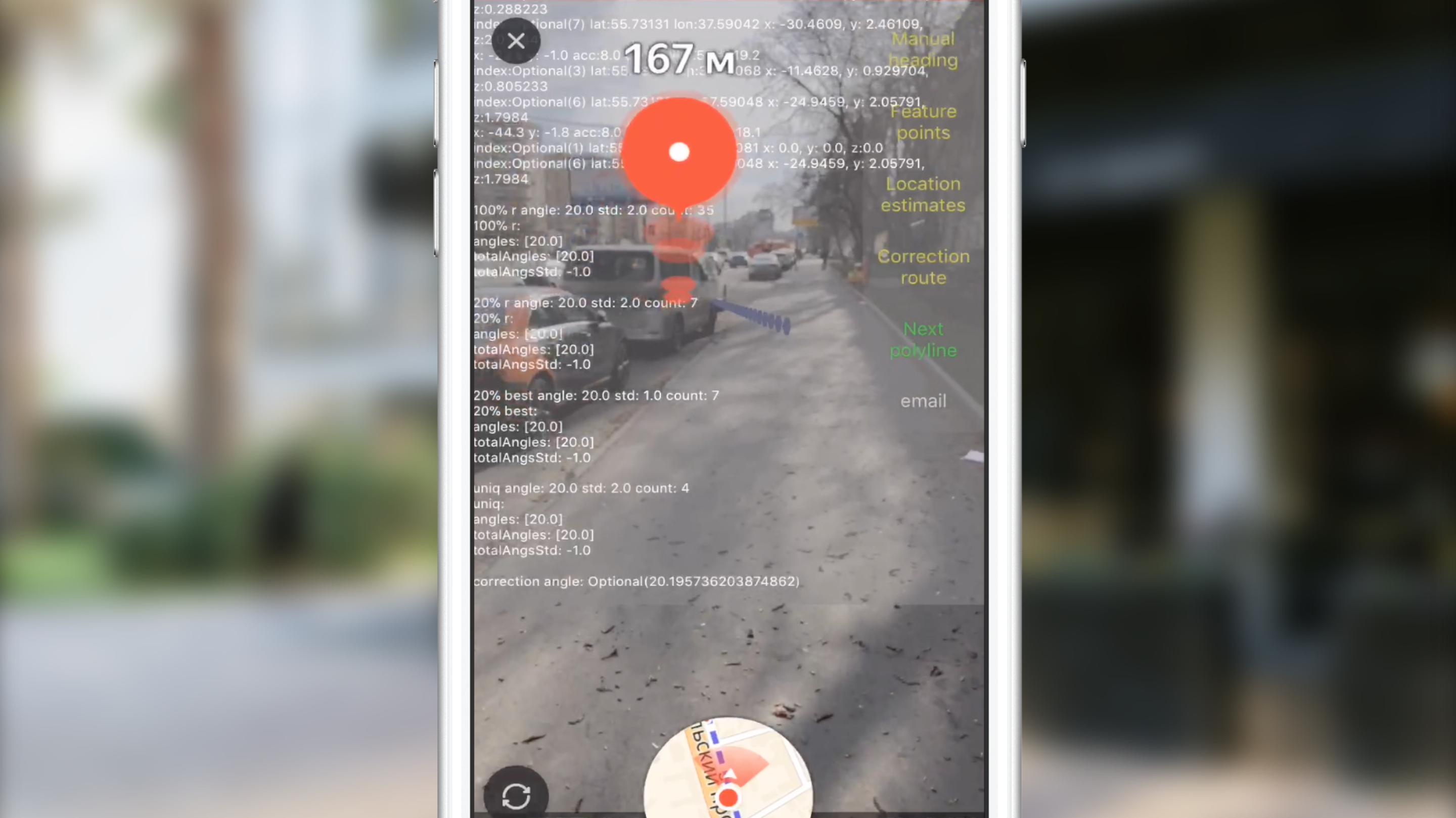
В конечном итоге (после 3-4 срабатываний) угол коррекции колеблется вблизи нуля и конечная точка маршрута отображается там, где и должна быть.

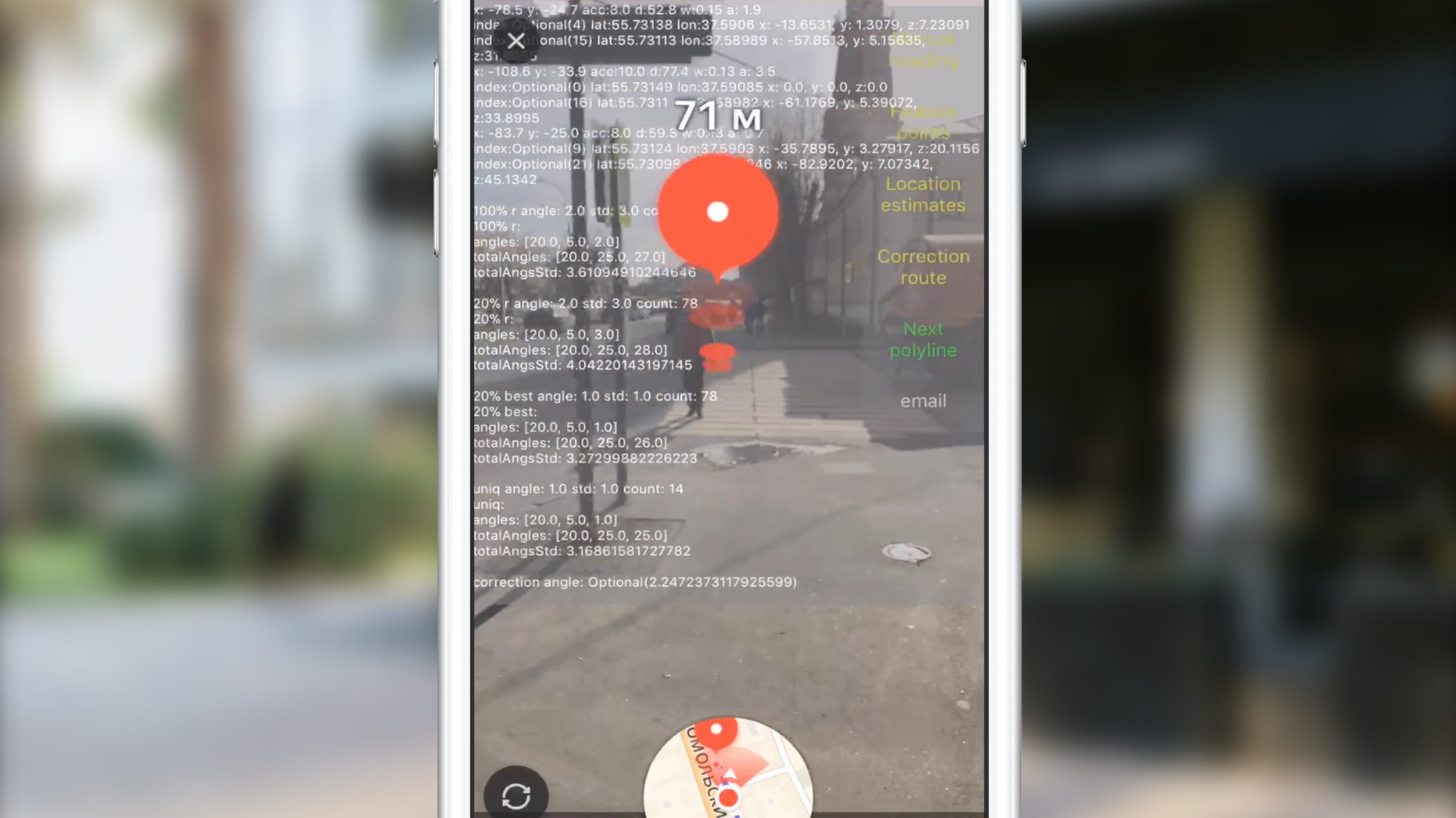
При необходимости мы загружали данные в небольшой скрипт на JS, который рендерил нам страничку с треками AR и CoreLocation.

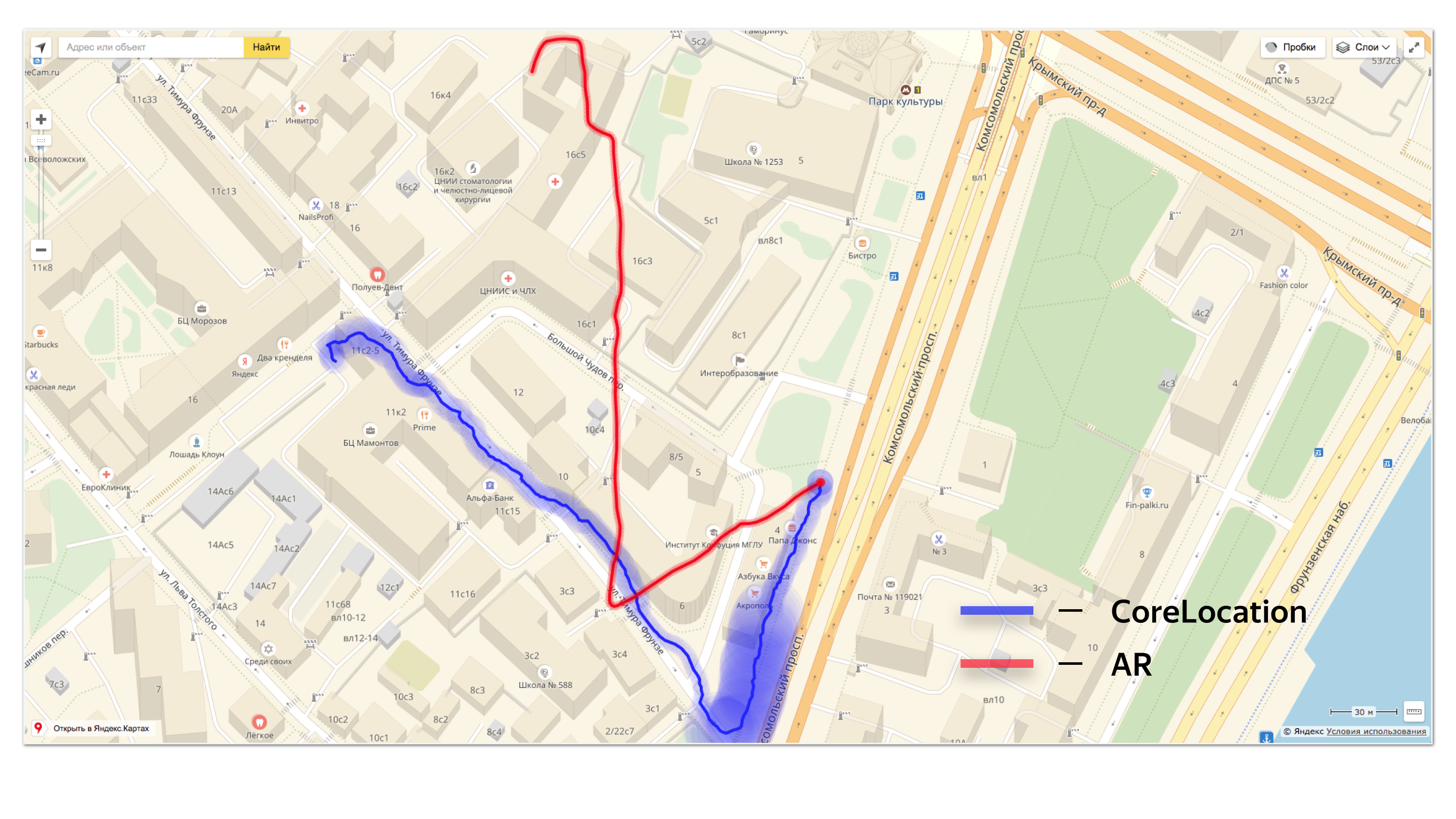
Также одним из видов тестирования являлась прогулка с заранее неправильно заданным направлением осей — когда мы использовали значение gravity для свойства worldAlignment и в ручную задавали направление осей. В этом случае мы также проверяли, что через определенное время алгоритм скорректирует направление осей должным образом. В конечном счете мы подобрали необходимый набор параметров и запустили наше решение в прод.

Вместо заключения

Если зайти в тематические каналы Slack, например, в этот, вы увидите, что люди до сих пор пытаются решить аналогичные проблемы. Для команды Карт проект пешеходной маршрутизации с дополненной реальностью стал отличным стартом и хорошим подспорьем для внедрения других возможностей с использованием AR. Приложение Яндекс.Карты попало в список лучших приложений с AR в AppStore в 2017 году. Надеюсь, наша история будет полезна сообществу Хабра.

Полезные ссылки

• сэмплы
• формулы конвертации
• ARKit+CoreLocation проект и туториалы
• много интересного про ARKit
• другие тоже корректируют направление осей
• история AR в одной картинке

Если наш опыт показался вам интересным, у нас есть что еще вам рассказать в нашем уютненьком блоге Яндекс.Карт.

Автор: trimonovds

Источник