Пара слов о том, что же такое филиппинский кроссворд
Филиппинский кроссворд – это такой вид графических головоломок, в которых с помощью множества пар чисел зашифрована картинка. Все кроссворды должны иметь единственное решение. Необходимо подобрать и соединить пары одинаковых чисел линиями так, результат удовлетворял следующим условиям (на которые я буду неоднократно ссылаться при дальнейшем изложении статьи):
- длина каждой линии должна соответствовать числам, расположенным на ее концах;
- линии не должны пересекаться друг с другом и проходить через одни и те же клетки;
- линии могут идти в вертикальном и горизонтальном направлениях, могут преломляться, но не могут проходить по диагонали.
Так как единица не имеет пары, то она закрашена по умолчанию. В результате решения кроссворда, когда все пары чисел (кроме единиц) соединены линиями, получается некоторый рисунок. Ознакомление с нижеприведенной gif-кой прольет свет на процесс решения филиппинского кроссворда:
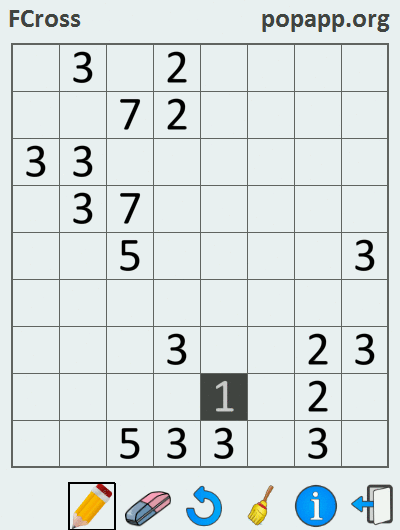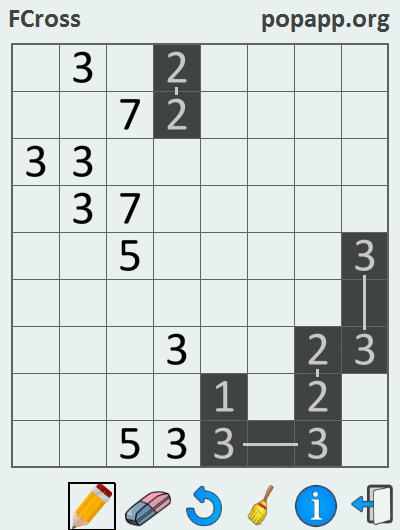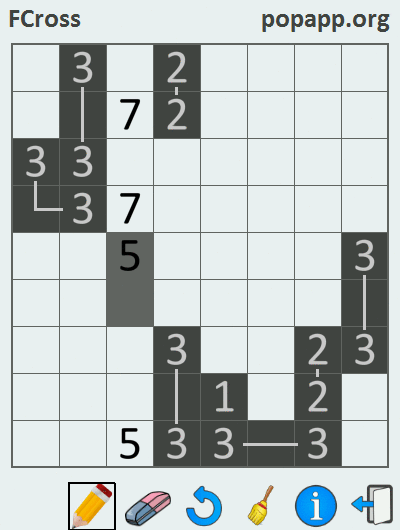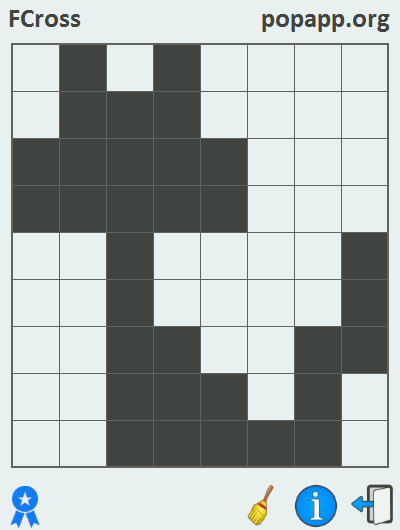
Данная задача решалась в среде Marmalade SDK с использованием языка программирования C++, в результате чего были собраны версии приложения под iOS и Android.
Представление состояния кроссворда в оперативной памяти
Сетка кроссворда состоит из ячеек, каждая из которых может быть закрашена или не закрашена (в разный момент времени), а так же иметь или не иметь в себе число (это свойство ячейки не меняется).
Минимальное число, используемое в моих кроссвордах – 1, максимальное – 9. В зависимости от того, каким образом линия проходит через клетку, она может быть закрашена несколькими способами (т.е. иметь несколько различных состояний).
Перечислим их:
- 1 – клетка не закрашена, т. е. линия через нее не проходит;
- 2 – клетка закрашена, но линия через нее также не проходит. В таком состоянии находятся все клетки с числом 1.
- 3 – линия проходит через клетку вертикально;
- 4 – линия проходит через клетку горизонтально;
- 5 – линия проходит через верхнюю и левую сторону квадрата клетки;
- 6 – линия проходит через нижнюю и левую сторону квадрата клетки;
- 7 – линия проходит через верхнюю и правую сторону квадрата клетки;
- 8 – линия проходит через нижнюю и правую сторону квадрата клетки;
- 9 – клетка является крайней клеткой линии и линия проходит через левую сторону квадрата клетки;
- 10 – клетка является крайней клеткой линии и линия проходит через правую сторону квадрата клетки;
- 11 – клетка является крайней клеткой линии и линия проходит через верхнюю сторону квадрата клетки;
- 12 – клетка является крайней клеткой линии и линия проходит через нижнюю сторону квадрата клетки.

В результате решения кроссворда пользователь получает следующее изображение:

Первое, что приходит на ум в качестве способа представления состояния кроссворда — это двумерный массив, т. е. матрица char-элементов. Тип char имеет размерность в 1 байт, т. е. позволяет хранить одно из 2^8 = 256 состояний.
Разобьем 8 бит байта на две группы: младшие и старшие биты. Получаем 4 бита в каждой группе, каждая группа дает возможность хранить 2^4 = 16 состояний.
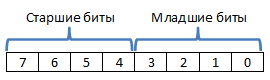
Таким образом, выделяем 4 старших бита для хранения информации о способе закрашивания ячейки, а 4 младших бита для хранения информации о числе, указанном в ячейке.
#define BYTE_NUMBER_PART 15 // в двоичной системе 00001111
#define BYTE_FLAG_PART 240 // в двоичной системе 11110000
struct JCStruct
{
bool Resolved; // признак решенности кроссворда
char FileName[255]; // имя файла задания
char W; // ширина сетки
char H; // высота сетки
char M[MAX_PUZZLE_HW][MAX_PUZZLE_ HW]; // матрица состояния ячеек
char Vector[CHANGE_VECTOR_SIZE][3]; // вектор изменений для возможности отмены действий [i, j, old_value]
int Vector_s; // vector start pointer (ссылается на первый элемент в очереди)
int Vector_e; // vector end pointer (ссылается на первый пустой элемент очереди)
int DigitsCnt; // Кол-во чисел в кроссворде (нужно для оптимизации алгоритма рисования чисел)
};
Объявляем функции, позволяющие с помощью побитового умножения получить значение старшей (флаг закраски) и младшей (число в ячейке) группы бит.
char GetNumberFromByte(char c) // функция возвращает число, указанное в ячейке. Если числа нет, то функция вернет 0
{
return c & BYTE_NUMBER_PART;
}
char GetFlagFromByte (char c) // функция возвращает флаг закраски ячейки. Вернет 0, если ячейка не закрашена
{
return c & BYTE_FLAG_PART;
}
Кодируем возможные флаги закрашивания ячеек кроссворда:
#define LN_ONE 16 // 00010000 клетка закрашена, но линия ч/з нее не проходит. для клеток с числом 1
#define LN_VERTICAL 32 // 00100000 линия проходит ч/з клетку вертикально;
#define LN_HORIZONTAL 48 // 00110000 линия проходит ч/з клетку горизонтально;
#define LN_LEFT_TOP 64 // 01000000 линия проходит ч/з нижнюю и правую сторону квадрата клетки;
#define LN_LEFT_BOTTOM 80 // 01010000 линия проходит ч/з верхнюю и правую сторону квадрата клетки;
#define LN_RIGHT_TOP 96 // 01100000 линия проходит ч/з нижнюю и левую сторону квадрата клетки;
#define LN_RIGHT_BOTTOM 112 // 01110000 линия проходит ч/з верхнюю и левую сторону квадрата клетки;
#define LN_RIGHT 128 // 10000000 клетка является крайней клеткой линии и линия проходит ч/з левую сторону клетки;
#define LN_LEFT 144 // 10010000 клетка является крайней клеткой линии и линия проходит ч/з правую сторону клетки;
#define LN_TOP 160 // 10100000 клетка является крайней клеткой линии и линия проходит ч/з нижнюю сторону клетки;
#define LN_BOTTOM 176 // 10110000 клетка является крайней клеткой линии и линия проходит ч/з верхнюю сторону клетки.
JCStruct* jc;
...
if (GetFlagFromByte(jc->M[i][j]) == LN_HORIZONTAL) // если клетка закрашена и линия проходит через нее по горизонтали
{
}
Далее весь функционал по отрисовке и изменению кроссворда реализуем используя вышеприведенные константы и функции.
Сценарий соединения двух чисел линиями
Пользователь тапает пальцем на какую-либо клетку с числом и ведет от нее линию до другой клетки с таким же числом. При отжатии пальца, если линия соответствует трем правилам, описанным в начале статьи, то линия фиксируется, результатом чего является фиксация состояния клеток матрице, через которые она проходит.
Текущая линия, которую пользователь ведем пальцем, в отражается в структуре CurrentLineStackStruct:
struct PointStruct
{
int x; // координата ячейки в сетке по горизонтали
int y; // координата ячейки в сетке по вертикали
};
struct CurrentLineStackStruct // стек, где будет храниться текущая линия
{
char num; // число, с которого начали линию
PointStruct stack[9]; // стек, в котором отражаются ячейки, через которой проходит текущая линия
char len; // указатель стека
};
CurrentLineStackStruct LineStack;
При инициализации, а также при каждом «отжатии» пальца от экрана этот стек инициализируется в исходное состояние вызовом следующей функции:
void ClearCurrentStack()
{
LineStack.len = 0; // длину стека обнуляем
LineStack.num = 0; // число, с которого стартует стек обнуляем
}
Обработка ведения пальца/стилуса по сетке кроссворда осуществляется функцией Redraw, которая возвращает true, если после обработки кроссворд требуется перерисовать, и false — в противном случае.
/*
jc - указатель на структуру JCStruct
DrawContext - структура-контекст, которая хранит текущие геометрические параметры отрисовки, в частности:
jc_screen_x - координата x левого верхнего угла сетки кроссворда
jc_screen_y - координата y левого верхнего угла сетки кроссворда
cell_wh - высота и ширина ячейки кроссворда
jc_screen_w - ширина всей сетки кроссворда
jc_screen_h - высота всей сетки кроссворда
*/
bool Redraw(int x, int y) // x,y -- координаты пальца-стилуса
{
if (!jc->Resolved) // Решенный кроссворд нельзя менять, можно только стереть все
if ((DrawContext.jc_screen_x <= x) && (x < DrawContext.jc_screen_x + DrawContext.jc_screen_w))
if ((DrawContext.jc_screen_y <= y) && (y < DrawContext.jc_screen_y + DrawContext.jc_screen_h))
{
// получаем координаты ячейки
int i = (x - DrawContext.jc_screen_x) / DrawContext.cell_wh;
int j = (y - DrawContext.jc_screen_y) / DrawContext.cell_wh;
// Если стек еще не начат, а на ячейке нет числа, то выходим
char n = GetNumberFromByte(jc->M[i][j]);
if ((LineStack.len == 0) && (n == 0)) return false;
// Если ячейка уже закрашена, то выходим
if (GetFlagFromByte(jc->M[i][j]) > 0) return false;
// смотрим, может мы вернулись назад на одну из предыдущих клеток стека
for (int s = 0; s < LineStack.len; s++)
if ((LineStack.stack[s].x == i) && (LineStack.stack[s].y == j))
{
// укорачиваем стек
LineStack.len = s + 1;
return true;
}
// Если стек еще не начат, то начинаем его с того числа, на которое нажали (то что это число следует из условия выше)
if (LineStack.len == 0)
{
// Стартуем стек
LineStack.len++;
LineStack.num = n; // запоминаем число, с которого начали
// записываем первую точку в стек
LineStack.stack[LineStack.len - 1].x = i;
LineStack.stack[LineStack.len - 1].y = j;
return true;
}
else // если стек уже начат, то значит это очередная ячейка
{
// смотрим, чтобы не было переполнения
// если есть еще куда добавлять ячейку (длина линии не может быть больше num)
if (LineStack.len < LineStack.num)
{
// смотрим, чтобы новая ячейка была соседней, по отношению к последней добавленной
if ((abs(LineStack.stack[LineStack.len - 1].x - i) == 1 && LineStack.stack[LineStack.len - 1].y == j)
||
(LineStack.stack[LineStack.len - 1].x == i && abs(LineStack.stack[LineStack.len - 1].y - j) == 1)
)
{
// соседняя ячейка должна быть либо пустой, либо иметь такое число, как и то,
// с которого начали, при этом длине линии не должно хвать именно этой одной клетки
if (n == 0 || LineStack.num == n && LineStack.len == n - 1)
{
LineStack.len++;
LineStack.stack[LineStack.len - 1].x = i;
LineStack.stack[LineStack.len - 1].y = j;
return true;
}
return false;
}
// Если новая ячейка не соседняя, но лежит на одной горизонтали с последней
if ((LineStack.stack[LineStack.len - 1].x != i) && (LineStack.stack[LineStack.len - 1].y == j))
{
int len = abs(i - LineStack.stack[LineStack.len - 1].x); // определяем длину приращения
int d = (i - LineStack.stack[LineStack.len - 1].x) / len; // определяем направление (знак приращения)
for (int s = 0; s < len; s++)
{
if (LineStack.len < LineStack.num)
{
// Если наткнулись на закрашенную ячейку
if (GetFlagFromByte(jc->M[LineStack.stack[LineStack.len - 1].x + d][j]) > 0)
{
if (s > 0) return true; // Если перед этим уже что-то добавили, то делаем перерисовку
else return false; // Если ничего еще не добавили, то перерисовка не нужна
}
n = GetNumberFromByte(jc->M[LineStack.stack[LineStack.len - 1].x + d][j]);
if (n > 0) // Если наткнулись на числовую ячейку
{
if (n != LineStack.num) // Если ее значение не равно числу, с которого начали
{
if (s > 0) return true; // Если перед этим уже что-то добавили, то делаем перерисовку
else return false; // Если ничего еще не добавили, то перерисовка не нужна
}
else // Если число в ячейке равно числу, с которого начали, т.е. n == LineStack.num
{
if (LineStack.num != LineStack.len + 1) // Если как раз не хватает только одной ячейки
{
if (s > 0) return true; // Если перед этим уже что-то добавили, то делаем перерисовку
else return false; // Если ничего еще не добавили, то перерисовка не нужна
}
}
}
LineStack.len++;
LineStack.stack[LineStack.len - 1].x = LineStack.stack[LineStack.len - 2].x + d;
LineStack.stack[LineStack.len - 1].y = j;
}
}
return true;
}
// Если новая ячейка не соседняя, но лежит на одной вертикали с последней
if ((LineStack.stack[LineStack.len - 1].x == i) && (LineStack.stack[LineStack.len - 1].y != j))
{
int len = abs(j - LineStack.stack[LineStack.len - 1].y); // определяем длину приращения
int d = (j - LineStack.stack[LineStack.len - 1].y) / len; // определяем направление (знак приращения)
for (int s = 0; s < len; s++)
{
if (LineStack.len < LineStack.num)
{
// Если наткнулись на закрашенную ячейку
if (GetFlagFromByte(jc->M[i][LineStack.stack[LineStack.len - 1].y + d]) > 0)
{
if (s > 0) return true; // Если перед этим уже что-то добавили, то делаем перерисовку
else return false; // Если ничего еще не добавили, то перерисовка не нужна
}
n = GetNumberFromByte(jc->M[i][LineStack.stack[LineStack.len - 1].y + d]);
if (n > 0) // Если наткнулись на числовую ячейку
{
if (n != LineStack.num) // Если ее значение не равно числу, с которого начали
{
if (s > 0) return true; // Если перед этим уже что-то добавили, то делаем перерисовку
else return false; // Если ничего еще не добавили, то перерисовка не нужна
}
else // Если число в ячейке равно числу, с которого начали, т.е. n == LineStack.num
{
if (LineStack.num != LineStack.len + 1) // Если как раз не хватает только одной ячейки
{
if (s > 0) return true; // Если перед этим уже что-то добавили, то делаем перерисовку
else return false; // Если ничего еще не добавили, то перерисовка не нужна
}
}
}
LineStack.len++;
LineStack.stack[LineStack.len - 1].x = i;
LineStack.stack[LineStack.len - 1].y = LineStack.stack[LineStack.len - 2].y + d;
}
}
return true;
}
return false;
}
else // если переполнение, то выходим
{
return false;
}
}
}
return false;
}
При «отжатии» пальца/стилуса делам обработку стека текущей линии. Необходимо понять, правильно ли нарисована линия, т. е. проверить ее на корректность, и в случае корректности обновить соответствующие ячейки матрицы.
/* тут мы должны принять решение о том,
что делать с текущим стеком линии - заносить ее в основную матрицу перед тем, как стереть
*/
void CheckCurrentLineStack()
{
// Если стек не пуст, если длина стека соответствует первому числу,
// если число, с которго начинали, равно числу в последней ячейке, то значит линия корректна
if ((LineStack.len > 0) && (LineStack.len == LineStack.num) &&
(LineStack.num == GetNumberFromByte(jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y]))
)
{
// Добавляем линию в вектор отмены
SetMatrixElement(jc, LineStack.stack[0].x, LineStack.stack[0].y/*, 1*/);
// перерисовываем текущий стек в матрицу М
// признаки того, где находится предыдущая/следующая клетка [0 - слева, 1 - справа, 2 - сверху, 3 - снизу]
char l_prev, l_next;
// сначала рисуем всю линию, кроме первой и последней клетки
for (int i = 1; i < LineStack.len - 1; i++)
{
// определяем положение пред клетки
if (LineStack.stack[i - 1].x + 1 == LineStack.stack[i].x) l_prev = 0;
if (LineStack.stack[i - 1].x - 1 == LineStack.stack[i].x) l_prev = 1;
if (LineStack.stack[i - 1].y + 1 == LineStack.stack[i].y) l_prev = 2;
if (LineStack.stack[i - 1].y - 1 == LineStack.stack[i].y) l_prev = 3;
// определяем положение след. клетки
if (LineStack.stack[i + 1].x + 1 == LineStack.stack[i].x) l_next = 0;
if (LineStack.stack[i + 1].x - 1 == LineStack.stack[i].x) l_next = 1;
if (LineStack.stack[i + 1].y + 1 == LineStack.stack[i].y) l_next = 2;
if (LineStack.stack[i + 1].y - 1 == LineStack.stack[i].y) l_next = 3;
l_prev = MAX(l_prev, l_next) * 10 + MIN(l_prev, l_next);
switch (l_prev)
{
case 32: jc->M[LineStack.stack[i].x][LineStack.stack[i].y] =
jc->M[LineStack.stack[i].x][LineStack.stack[i].y] + LN_VERTICAL; break;
case 31: jc->M[LineStack.stack[i].x][LineStack.stack[i].y] =
jc->M[LineStack.stack[i].x][LineStack.stack[i].y] + LN_LEFT_TOP; break;
case 30: jc->M[LineStack.stack[i].x][LineStack.stack[i].y] =
jc->M[LineStack.stack[i].x][LineStack.stack[i].y] + LN_RIGHT_TOP; break;
case 21: jc->M[LineStack.stack[i].x][LineStack.stack[i].y] =
jc->M[LineStack.stack[i].x][LineStack.stack[i].y] + LN_LEFT_BOTTOM; break;
case 20: jc->M[LineStack.stack[i].x][LineStack.stack[i].y] =
jc->M[LineStack.stack[i].x][LineStack.stack[i].y] + LN_RIGHT_BOTTOM; break;
case 10: jc->M[LineStack.stack[i].x][LineStack.stack[i].y] =
jc->M[LineStack.stack[i].x][LineStack.stack[i].y] + LN_HORIZONTAL; break;
}
}
// определяем для первой клетки
if (LineStack.stack[1].x + 1 == LineStack.stack[0].x)
jc->M[LineStack.stack[0].x][LineStack.stack[0].y] = jc->M[LineStack.stack[0].x][LineStack.stack[0].y] + LN_RIGHT;
if (LineStack.stack[1].x - 1 == LineStack.stack[0].x)
jc->M[LineStack.stack[0].x][LineStack.stack[0].y] = jc->M[LineStack.stack[0].x][LineStack.stack[0].y] + LN_LEFT;
if (LineStack.stack[1].y + 1 == LineStack.stack[0].y)
jc->M[LineStack.stack[0].x][LineStack.stack[0].y] = jc->M[LineStack.stack[0].x][LineStack.stack[0].y] + LN_BOTTOM;
if (LineStack.stack[1].y - 1 == LineStack.stack[0].y)
jc->M[LineStack.stack[0].x][LineStack.stack[0].y] = jc->M[LineStack.stack[0].x][LineStack.stack[0].y] + LN_TOP;
// определяем для последней клетки
if (LineStack.stack[LineStack.len - 2].x + 1 == LineStack.stack[LineStack.len - 1].x)
jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] =
jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] + LN_RIGHT;
if (LineStack.stack[LineStack.len - 2].x - 1 == LineStack.stack[LineStack.len - 1].x)
jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] =
jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] + LN_LEFT;
if (LineStack.stack[LineStack.len - 2].y + 1 == LineStack.stack[LineStack.len - 1].y)
jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] =
jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] + LN_BOTTOM;
if (LineStack.stack[LineStack.len - 2].y - 1 == LineStack.stack[LineStack.len - 1].y)
jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] =
jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] + LN_TOP;
DrawContext.need_save = true;
}
}
Отрисовка кроссворда и текущей линии
Отрисовка кроссворда делится на следующие этапы:
- Рисование закрашенных ячеек матрицы;
- Рисование ячеек стека текущей линии;
- Рисование линий на закрашенных ячейках матрицы;
- Рисование линий на ячейках стека текущей линии;
- Рисование чисел на ячейках.
Дабы не излишне не перегружать статью кодом, приведем только листинг самого из интересного из вышеуказанных пунктов.
if (jc->Resolved == false) // Если кроссворд не решен
{
//Рисуем на клетках соединительные линии
Iw2DSetColour(ColorSchema.JCCellLineColor);
for (int i = 0; i < jc->W; i++)
for (int j = 0; j < jc->H; j++)
{
n1 = jc->M[i][j] & BYTE_FLAG_PART;
switch (n1)
{
case LN_HORIZONTAL:
Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + 0,
DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1
),
CIwFVec2(DrawContext.cell_wh - 0, 3)
);
break;
case LN_VERTICAL:
Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1,
DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + 0),
CIwFVec2(3, DrawContext.cell_wh - 0)
);
break;
case LN_RIGHT:
Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + 0,
DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1),
CIwFVec2(4, 3)
);
break;
case LN_LEFT:
Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i + 1)* DrawContext.cell_wh - 4,
DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1),
CIwFVec2(4, 3)
);
break;
case LN_BOTTOM:
Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1,
DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + 0),
CIwFVec2(3, 4)
);
break;
case LN_TOP:
Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1,
DrawContext.jc_screen_y + (j + 1)* DrawContext.cell_wh + 0 - 4),
CIwFVec2(3, 4)
);
break;
case LN_RIGHT_BOTTOM:
// горизонтальная полулиния
Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + 0,
DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1),
CIwFVec2(DrawContext.cell_wh / 2 - 1 + 3, 3)
);
// вертикальная полулиния
Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1,
DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + 0),
CIwFVec2(3, DrawContext.cell_wh / 2 - 1 + 3)
);
break;
case LN_RIGHT_TOP:
// горизонтальная полулиния
Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + 0,
DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1),
CIwFVec2(DrawContext.cell_wh / 2 - 1 + 3, 3)
);
// вертикальная полулиния
Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1,
DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1),
CIwFVec2(3, DrawContext.cell_wh / 2 - 1 + 3)
);
break;
case LN_LEFT_BOTTOM:
// горизонтальная полулиния
Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1,
DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1),
CIwFVec2(DrawContext.cell_wh / 2 - 1 + 3, 3)
);
// вертикальная полулиния
Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1,
DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + 0),
CIwFVec2(3, DrawContext.cell_wh / 2 - 1 + 3)
);
break;
case LN_LEFT_TOP:
// горизонтальная полулиния
Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1,
DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1),
CIwFVec2(DrawContext.cell_wh / 2 - 1 + 3, 3)
);
// вертикальная полулиния
Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1,
DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1),
CIwFVec2(3, DrawContext.cell_wh / 2 - 1 + 3)
);
break;
}
}
}
Проверка решенности кроссворда
В связи с тем, что корректность каждой нарисованной линии проверяется в момент ее рисования, все существующие линии соответствуют трем правилам, приведенным в начале статьи. А это в свою очередь означает, что для проверки решенности кроссворда нам достаточно убедиться, что все клетки с числами закрашены.
/* функция вернет 0, если кроссворд решен,
иначе координату первой встретившейся некорректной ячейки,
не соответствующей требуемому конечному решению
*/
int CheckJC(JCStruct * p)
{
for(int i = 0; i < p->W; i++)
for(int j = 0; j < p->H; j++)
if(GetNumberFromByte(p->M[i][j]) > 1) // считаем, что цифра 1 всегда закрашена по умолчанию, по этому ее не проверяем
if(GetFlagFromByte(p->M[i][j]) == 0) // если ячейка не закрашена
return 100 * (i + 1) + (j + 1);
return 0;
}
Автор: akk0rd87





