
Современные криптографические устройства требуют надежной системы генерации и хранения ключей. В этой статье мы рассмотрим одну из наиболее перспективных и рассматриваемых сейчас решений: физически неклонируемые функции, основанные на частотах.
Физически неклонируемые функции (англ. Physical unclonable function, PUF) позволяют конструировать качественные системы генерации и хранения ключа, устойчивые к взломам. Также технология PUF широко используется в аутентификации данных из ненадежных источников и верификации подлинной продукции: нелегальный рынок подделок, вносящий немалый вклад в теневую сферу и приносящий многомиллионные убытки компаниям-производителям, - большая проблема для современной экономики.
Краткое описание принципа работы и применений физически неклонируемых функций
Пусть мы имеем систему, содержащую на неком физическом носителе секретный ключ, с помощью которого входные данные преобразуются в выходные. Если мы получим ключ, то будем в состоянии для любых входных данных получить валидные выходные данные. В случае физически неклонируемой функции физическая среда и есть ключ, несущий в себе некую уникальную информацию.
Физически неклонируемая функция (ФНФ, PUF) - функция, использующая необратимые уникальные особенности физической среды. Используется принцип того, что невозможно получить две абсолютно идентичные физические системы. Это можно пояснить на следующем наглядном для представления, но сложном для производства примере.
![Строение оптической ФНФ. Взято из [3] Строение оптической ФНФ. Взято из [3]](https://www.pvsm.ru/images/2021/12/13/fizicheski-nekloniruemye-funkcii-osnovannye-na-chastotah-2.png)
Возьмем расплавленной стекло и добавим в него пузырьки воздуха, затем охладим его и вырежем брусок. Пустим на полученный брусок стекла лазерный луч, который будем считать аргументом нашей функции, а возникшую в результате этого интерференционную картину, вызванную множественными преломлениями луча в наполненном пузырьками бруске - значением функции при данном аргументе. Обычно аргументы PUF называют запросом (англ. challenge), а значения функции - ответом (англ. response).
Практически невозможно идентичными действиями получить два одинаковых бруска, поэтому каждая такая функция будет уникальна, и ее невозможно будет скопировать, т.е. она неклонируема.
К ФНФ предъявляют следующие требования:
-
Невозможность математического описания модели. Нельзя, чтобы, имея достаточно большое количество пар запрос-ответ, можно было как-то математически описать или смоделировать функцию.
-
Уникальность. Множество пар запрос-ответ должно быть случайным и не должно быть двух запросов, которые отвечают одному ответу.
-
Достижение «лавинного эффекта», т. е. изменение единственного входного бита запроса должно в равной степени изменять все биты ответа. Иными словами, все выходные биты должны зависеть от каждого входного бита.
Область применений ФНФ очень широка, например генерация и хранение случайного ключа шифрования. Также они используются для аутентификации устройств: произведенное изделие оснащается PUF и производитель сохраняет приватный список пар запрос-ответ, полученный от PUF. Затем, при верификации устройства производитель проверит записанные данные с теми парами, которые выдает исследуемое устройство. Если оно было незаконно скопировано, то они будут различаться из-за невозможности клонирования.
Физические принципы, используемые для построения ФНФ, разнообразны:
-
Особенности физических сред, такие как структура бумаги, оптические среды и т. д.;
-
Уникальные параметры цифровых схем и элементов, такие как времена задержек сигналов, пороговые напряжения транзисторов;
-
Состояние памяти после включения или сброса;
-
Частоты компонентов, такие как кварцевые резонаторы и генераторы.
Рассмотрим в нашей статье подробнее последнюю группу решений.
Решения, основанные на частотах
Как и в общем случае, методы построения подобных схем довольно разнообразны. Рассмотрим основные и наиболее часто применяемые из них.
Ring oscillator PUF
Кольцевой генератор состоит из нечетного числа последовательно включенных инверторов, замкнутых в «кольцо». Любая комбинационная схема не работает мгновенно, т. е. есть некая задержка распространения (англ. propagation delay) сигнала между входом и результатом на выходе, связанная с неидеальностью элементов (наличием паразитных емкостей и сопротивлений, ведущих к инерционности работы).
![Модель кольцевого генератора. Взято из [4] Модель кольцевого генератора. Взято из [4]](https://www.pvsm.ru/images/2021/12/13/fizicheski-nekloniruemye-funkcii-osnovannye-na-chastotah-3.png)
Мысленно разорвем цепь и представим, что на ее входе присутствует прямоугольный сигнал. На выходе цепи из-за нечетного количества инверторов возникнет инвертированный сигнал, но не сразу, а с задержкой
где τ - задержка одного инвертора. Таким образом, сигнал на входе и на выходе будет полностью совпадать, если общая задержка инверторов будет составлять ровно полпериода прямоугольного сигнала, и подобный сигнал может распространяться в исходной замкнутой цепи. Его частота составит
Данная модель также имеет вход включения (enable), разрешающий или запрещающий колебания генератора. При единице на входе элемент И-НЕ превращается в инвертор и дополняет генератор, а при нуле элемент И-НЕ всегда на выходе выдает единицу и генератор выключается.
Частота генерируемого сигнала напрямую зависит от задержек, вносимых инверторами - полупериод колебаний равен их сумме. Таким образом, в данной модели построения ФНФ измеряемая частота генерации, зависящая от индивидуальных особенностей инверторов, является уникальным и неклонируемым параметром.
Рассмотрим наиболее распространенную модель построения самой функции, рассмотренной в [5] и основанной на кольцевых генераторах. она представлена на следующем рисунке.
![Модель ring oscillator PUF. Взято из [5] Модель ring oscillator PUF. Взято из [5]](https://www.pvsm.ru/images/2021/12/13/fizicheski-nekloniruemye-funkcii-osnovannye-na-chastotah-6.png)
Имеются два множества кольцевых генераторов, из которых в зависимости от входного запроса, подаваемого на мультиплексоры, выбирается по одному и при помощи асинхронных счетчиков измеряются их частоты. Затем результаты сравниваются на компараторе, и один из выходных битов отклика является результатом сравнения. Следующие биты отклика формируются на мультиплексорах выбором (в зависимости от запроса) следующих двух генераторов.
Loop и TERO PUF
Модель Loop PUF формирует замкнутую цепочку n блоков задержек, которые в схожей с ring-oscillator PUF манере колеблются с определенной частотой. Каждый блок задержки из m настраиваемых задерживающих элементов, которые в зависимости от входного бита настраивают прохождение сигнала по одному из двух возможных путей. Таким образом, блок задержек управляется m-битной частью входного запроса размера nm бит и измерением частоты генератора.
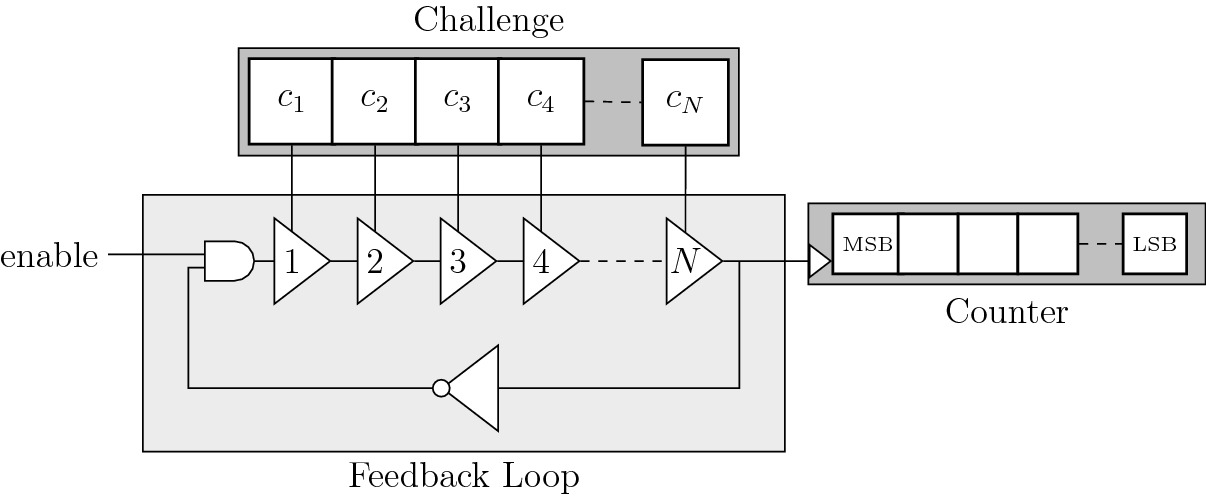
n-битный выходной отклик формируется последовательным проходом по n блокам входного запроса. Недостаток данного метода заключается в том, что для разных запросов используются одни и те же структуры, что представляет собой уязвимость для взлома.
Модель TERO PUF использует неизбежное кратковременное появление осцилляций при переходе двух скрещенных инверторов в стабильное состояние, и формирует выходной отклик из количества этих осцилляций.
Список литературы
[1] Alexander Wild, Georg T. Becker, Tim Güneysu, A Fair and Comprehensive Large-Scale Analysis of Oscillation-Based PUFs for FPGAs. 27th International Conference on Field Programmable Logic and Applications (FPL), 2017.
[2] Shitai Joshi, Elias Kougianos, Saraju P.Mohanty, Everything You Wanted to Know about PUFs. IEEE Potentials, 2017.
[3] Roel Maes, Ingrid Verbauwhede, Physically Unclonable Functions: A Study on the State of the Art and Future Research Directions. 2010.
[4] Michael Patterson, Joseph Zambreno, Chris Sabotta, Sudhanshu Vyas, Aaron Mills, Ring Oscillator PUF Design and Results. Reconfigurable Computing Laboratory, Iowa State University.
[5] Venkata P. Yanambaka, Saraju P. Mohanty, Elias Kougianos, Prabha Sundaravadivel, Jawar Singh, Dopingless Transistor Based Hybrid Oscillator Arbiter Physical Unclonable Function. University of North Texas, 2017.
Автор:
tmbengnr






