Из этой статьи вы узнаете:
-
Что такое схемы разделения секрета и с чем их едят
-
Чем хороши пороговые схемы
-
Идея схемы Миньотта
-
Идея схемы Карнина-Грина-Хеллмана
-
Где применяются такие схемы
Что такое схемы разделения секрета и зачем они нужны?
Начну свое повествование с примера, описанного в книге неизвестного бельгийского автора "Gent und seine Schönheiten". В городе Генте была построена ратушная башня, в одной из комнат которой хранились очень важные документы. Эти документы лежали в шкафу, закрывавшемся на три замка, шкаф - в яйце, яйцо - в утке, утка - в зайце... Один ключ от шкафа хранился у фогта, а два других – у главного шеффена. В секретной комнате было две двери, каждая с тремя замками. Ключи от этих замков находились во владении различных цехов. Таким образом, получить доступ к документам могли только совместно собравшиеся представители трех цехов, фогт и шеффен.
На этом ярком примере можно понять основной смысл схем разделения секрета. Чтобы получить доступ к зашифрованным данным, необходимо присутствие нескольких доверенных лиц, у каждого из которых будет часть секрета. Собрав все части вместе, пользователи могут довольствоваться расшифрованной информацией.
Такие протоколы используются в случае возможности компрометации одного или нескольких участников схемы разделения секрета. Чем больше хранителей различных "ключей от шкафов и дверей", тем больше вероятность того, что секрет восстановится честным способом и информация не окажется в руках злоумышленников.
Основные понятия
В своей статье я буду использовать следующие установившиеся термины:
-
Доля секрета - некоторая уникальная для каждого участника процесса информация, помогающая восстановить секрет
-
Дилер - доверенное лицо, которое производит распределение долей секрета между участниками
-
Разделение секрета - фаза подсчета и раздачи долей секрета
-
Восстановление секрета - фаза сбора долей секрета и подсчета самого́ секрета
Пороговые схемы разделения секрета
В городе Генте для получения доступа к документам обязательным условием было присутствие всех хранителей ключа. Но что если фогт заболеет, а представитель одного из цехов потеряет ключ? Неужели тайны города Генте будут навсегда утеряны?
Что было с городскими документами история умалчивает, но понимая последствия подобных протоколов разделения секрета, люди придумали пороговые (t, n) схемы. Имея n частей секрета, можно восстановить его, используя только t из них. Если любая группа из t-1 или меньше сторон не могут восстановить секрет, то такая схема называется совершенной. В случае, когда размер долей секрета такой же, как и у самого секрета, то схема называется идеальной.
Если бы работники администрации города Генте знали о таком методе, они бы выбрали n хранителей ключей, но построили бы систему безопасности таким образом, что нужно было бы не менее t из n участников процесса чтобы получить доступ к секрету. Однако, в случае заговора, несколько хранителей ключа, количество которых было бы меньше t, не смогли бы открыть двери и украсть документы.
Рассмотрим далее несколько пороговых схем, которые не так популярны, как, например, схема Блэкли и схема Шамира.
Схема Миньотта
Данный метод основан на китайской теореме об остатках. Звучит она следующим образом:
Если натуральные числа
взаимно просты, то для любых чисел
таких, что <img class="formula inline" source="0leq r_i <a_i" alt="0leq r_i при всех
найдется число
которое при делении на
дает остаток
для всех
. Более того, если найдутся два таких числа
и
, то
.
Иными словами, теорема позволяет утверждать о единственности решения системы:
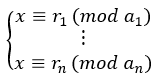
В схеме Миньотта используются так называемые последовательности Миньотта – последовательности взаимно простых положительных чисел
<img class="formula inline" source="p_1<p_2<⋯<p_n " alt="p_1<p_2<⋯
такие, что <img class="formula inline" source="prod _{i=0} ^{t-2} p_{n-i}< prod _{i=1} ^{t} p_{i}" alt="prod _{i=0} ^{t-2} p_{n-i}при том, что n – целое, 
и 
.
Наконец, опишем алгоритм схемы разделения секрета. Имеется открытая последовательность Миньотта, из которой выбирается случайным образом секрет S. Обозначим
и потребуем чтобы <img class="formula inline" source="β<S<α" alt="β<S.
Задача дилера в этом случае заключается в вычислении долей секрета 
по формуле 
и распределении их между участниками.
Восстанавливается секрет с помощью t значений 
. Составляется система:
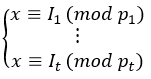
По китайской теореме об остатках она имеет единственное решение, лежащее в пределах 
так как <img class="formula inline" source="S<α" alt="S. В случае попытки решить систему имея t-1 долей секрета, можно считать, что 
где 
– единственное решение системы с t-1 уравнениями. Отсюда следует, что подобрать секрет будет тем сложнее, чем больше будет последовательность Миньотта, то есть чем выше значение 
.
Очевидно, что схема разделения секрета Миньотта не обладает высокой криптографической стойкостью, так как в худшем случае может быть взломана перебором, то есть не является совершенной. Более того, во многих случаях данный метод может быть неудобен требованиями ограничения секрета и генерации больших последовательностей Миньотта, что является довольно ресурсоемкой задачей. Так как размер секрета совпадает с его долей, то схема – идеальная.
Схема Карнина-Грина-Хеллмана
Следующая схема основана на том, что невозможно однозначно решить систему c t неизвестными, имея меньше, чем t уравнений. Все действия происходят в конечном поле. На этапе разделения секрета случайным образом выбирается n+2 различных векторов 
размерности t так, чтобы ранг любой матрицы размером t x t, составленной из этих векторов, был равен t (то есть все вектора выбираем попарно линейно независимыми). При этом значения 
являются открытыми. Секретом S будет служить скалярное произведение 
а долями секрета – скалярные произведения 
.
Восстановление секрета происходит с помощью решения системы линейных алгебраических уравнений из t уравнений и t неизвестных относительно компонент вектора U:
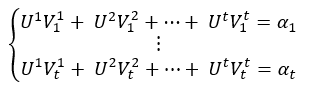
Система имеет единственное решение, так как на этапе распределения секрета выбирались линейно независимые векторы, значит определитель матрицы не равен нулю. Найдя вектор U, легко восстановить секрет путем вычисления скалярного произведения 
.
Если злоумышленник получит меньше, чем t значений, система будет иметь бесконечное количество решений и любое из них равновероятно может быть искомым секретом. Это означает, что схема Карнина-Грина-Хеллмана является совершенной. Однако, размер каждой доли секрета в t раз больше самого секрета, что делает схему не идеальной.
Применение схем разделения секрета
Пороговые (t, n) схемы разделения секрета используются в пороговых криптосистемах. Такие криптосистемы позволяют расшифровать сообщение некоторой группой из не менее, чем t участников, между которыми распределен секрет. В качестве секрета в пороговых криптосистемах используется ключ расшифрования, в то время, как ключ шифрования является общим и открытым.
Для создания пороговых криптосистем могут использоваться такие системы открытого шифрования, как:
-
Криптосистема RSA
-
Криптосистема Эль-Гамаля
Пороговые криптосистемы используются во многих областях, например, для хранения секретного ключа центра сертификации, в государственной и военной сферах, облачных средах и схемах электронного голосования.
Источники
-
Karnin E. D., Greene J. W., Hellman M. E. “On Secret Sharing Systems” // IEEE, 1983.
-
Шнайер Б. “Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си” – Триумф, 2002
-
http://cryptowiki.net/index.php?title=Схемы_разделения_секрета._Пороговая_криптография
Автор: Анастасия Шеренешева
