Привет, %username%!
Мне, как ни разу не профессиональному математику и криптографу, редко бывает сразу понятно как устроен тот или иной алгоритм. И тем более, почему его выбирают.
Так и с новым стандартом SHA-3. Выбрали какой-то Keccak, спасибо камраду NeverWalkAloner, привел его описание. Но лично мне так и не стало понятно как он работает и в чем его фишка. Давайте разбираться.
В конце статьи будет небольшой бонус параноикам в виде информации к размышлению о стойкости SHA-2
Для начала, скажу, что все хэши стремятся быть максимально похожими на так называемый «Случайный оракул». Поэтому, для начала немного про него.
Случайный оракул — это абстрактный черный ящик, обладающий бесконечной памятью и работающий по следующему алгоритму:
- Получает на вход строку и смотрит, работал ли он с ней ранее.
- Если нет, то генерирует истинно случайное число (м.б. фиксированной длины, а может и вообще любое в диапазоне 0 -бесконечность, тут формулировки разнятся) и сохраняет в себе пару строка-число.
- Если да, то выдает ранее сохраненное число для этой строки.
Похоже на хэш, да? Только с тем фундаментальным отличием, что связь между хешируемой строкой и результатом вычислить в принципе невозможно. Идем дальше.
Еще один бич всех хэш функций — это коллизии. Не те, что могут по определению быть, потому что у хэша размер фиксированный, а те которые случаются гораздо раньше, плохии коллизии (1 и 2 рода). У большинства современных реализаций хэшей используются различные т.н. функции сжатия, преобразующие блок текста размером, скажем, n, в блок размером, скажем, n/2. И пока что никто не доказал, что можно построить функцию сжатия, устойчивую к коллизиям.
И тут авторы Keccak пошли другим путем. Они решили использовать псевдослучайные перестановки, в которых коллизий не может быть по определению. Остановимся на этом моменте подробнее.
Вспомним как работает любой блочный шифр.
Он берет блок открытого текста фиксированной длины, ключ, и сопоставляет им шифротекст такой же длины. Это сопоставление однозначно, иначе мы бы не смогли расшифровать блок обратно. Таким образом, идеальный блочный шифр(скажем, с размером блока 128 бит) можно представить как нефиговых размеров таблицу, в первой строке которой будут все возможные ключи(2128), в первой колонке — все возможные открытые тексты(тоже 2128), а на пересечении строк и столбцов будут стоять истинно случайным образом сгенерированные шифроблоки, причем отношение открытый блок-ключ-зашифрованный блок будет однозначным.
В математике такое взаимно однозначное отношение называется биекцией.
Заметьте, что в любой строке и любой колонке можно встретить все возможные комбинации бит (длины 2128 для нашего случая) в случайном порядке, причем каждая комбинация будет встречаться единожды. Это и есть перестановки. Ну а в реальной жизни используются псевдослучайные перестановки, описываемые алгоритмами. Потому что такую вот таблицу сгенерировать нереально.
Думаю, теперь и неспециалистам ясно, что коллизиям тут просто неоткуда взяться. Иначе, различным шифроблокам мог бы сопоставляться один и тот же открытый блок и наоборот.
А каким местом тут хэши и Keccak?
Авторы Keccak придумали простую (если разобраться) схему, т.н. Sponge функцию, или по-русски губку.
Внутри этой «губки» имеется состояние(размером в 1600 бит для SHA-3), к которому на каждом раунде применяется одна и та же функция, реализующая псевдо-случайную перестановку.
То есть, это по сути, блочный шифр без ключа с размером блока 1600 бит. И если мы заполним состояние нулями, выполним 10 раундов (10 раз применим их функцию f) в одну сторону, а потом столько же в обратную(с функцией, обратной f), то опять получим нули. Биекция во всей красе. Но это еще не всё.
Чтобы захэшировать строку, нужно сначала разбить её на куски определенного размера и на каждом раунде ксорить(подмешивать) их не ко всему 1600 битному состоянию, а только к его началу размера r. Тут уж я вставлю ту самую картинку, теперь она имеет смысл.
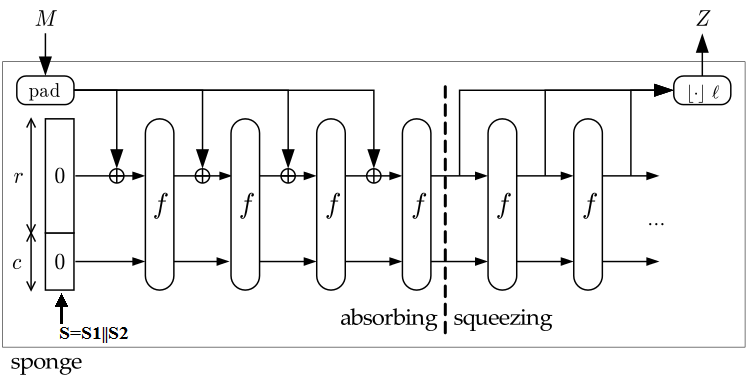
То есть, на каждом раунде очередной кусок строки подмешивается только к части состояния, тогда как псевдо-случайная перестановка f обрабатывает всё состояние целиком, размазывая таким образом строку по состоянию и делая его зависимым от всей строки.
Это так называемый этап «впитывания». И теперь понятно, почему он так называется. Надеюсь, вам тоже. Осталось чуть-чуть!
Чтобы получить собсно хэш, мы продолжаем применять функцию перестановки f к состоянию, и на каждом этапе копируем из него лишь кусок размера r до тех пор, пока не получим хэш необходимой длины(эти куски мы конкатенируем). Это т.н. «отжатие» губки. Вот и всё.
Из-за того, что мы используем не всё состояние, а лишь его часть, мы не можем ничего сказать о связи входных и выходных данных. И авторы Keccak доказали, что стойкость такой конструкции неотличима от случайного оракула с размером «ответа», равным с/2 (всё состояние имеет размер с+r) при условии, что f — идеальная функция перестановки(та табличка из идеального блочного шифра, только из двух столбцов, потому, что ключа нет). То есть, чтобы получить хэш с доказанной математически стойкостью в 512 бит, нужно сделать размер параметра с (независимой части состояния) 512*2=1024 бита. Таким образом, при состоянии размером 1600 бит для 512 битного хэша мы 1024 бита не трогаем, а к первым 576 подмешиваем часть хэшируемой строки на каждом раунде.
Не обошлось без ложки дёгтя:
функция f у авторов хорошо описана, она состоит из пяти довольно простых обратимых операций(даже анимашки есть), внешне хорошая и её пока не поломали, нет гарантий, что её не поломают в будущем. Зато, если это произойдет, нужно будет заменить лишь f(например на нормальный блочный шифр вроде AES, только без ключа), а «губку» можно оставить, т.к. она (доказано) стойкая при стойкой f.
На этом у меня всё, надеюсь, получилось более-менее разложить всё по полочкам. Спасибо ребятам с pgpru за консультацию про биекции, а авторам keccak за код обратных функций, из которых состоит функция f(есть в пакете keccak-tools на их сайте).
На java выглядит примерно так
int func(int x, int a, int b, int c)
{
return (ror(x, a) ^ ror(x, b) ^ (x >>> c));
}
Потом выяснилось, что это 2 функции sigma1 и sigma2 из SHA-2.
И я чего то заморочился, потому что выглядят они красиво, а как работают – хз.
Оригинальные a,b, с из SHA-2 и HC-128
{7, 18, 3} и {17, 19, 10}
Я решил посчитать хитрый период, взяв бесконечный цикл f(f(f(f...(1)))) и ища повтор. Оказалось, что у функции с оригинальными константами такой «период» был равен 49146, а мне удалось найти кучу пар, у которых «период» был 131070. И, как и у оригинальных констант, множества, которые генерировались при таком цикле, не пересекались. Например
{22, 13, 3} и {18, 4, 9},
{24, 15, 2} и {18, 3, 4}
Так вот, функция func, если посчитать период нормально, пробегая от 0 до 232-1 имеет период 232, то есть опять же, биективна.
Далее цитата из топика с pgpru:
Вот даже известные криптографы пытались исследовать этот АНБ-шный трюк, но к какому-то определённому мнению вроде не пришли.
The σ0 and σ1 GF(2)- linear mappings are one to one (in order to check this property, we computed the 32x32 GF(2) matrices representing σ0 and σ1, and checked that the kernel of this matrix was restricted to the null vector).
«Evaluation Report Security Level of Cryptography – SHA-256» © Dr. Helena Handschuh, Dr. Henri Gilbert
σ0 and σ1 have both the property to increase the Hamming weight of low-weight inputs. This increase is upper bounded by a factor of 3. The average increase of Hamming weight for low-weight inputs is even higher if three rotations are used instead of two rotations and one bit-shift. However, a reason for this bit-shift is given by the next observation. In contrast to all other members of the MD4-family including SHA-1, rotating expanded message words to get new expanded message words is not possible anymore (even in the XOR-linearized case). This is due to the bitshift being used in σ0 and σ1.
«Preliminary Analysis of the SHA-256 Message Expansion» © Norbert Pramstaller, Christian Rechberger, Vincent Rijmen
We show that the disturbance-correction strategy is applicable to the SHA-256 architecture and we prove that functions Σ, σ are vital for the security of SHA-256 by showing that for a variant without them it is possible to find collisions with complexity 264 hash operations
The S-boxes σ0 and σ1 play a similar role: they provide nonlinearity and better diffusion for the message expansion.
«Analysis of simplified variants of SHA-256» © Krystian Matusiewicz, Josef Pieprzyk, Norbert Pramstaller, Christian Rechberger, Vincent Rijmen.
В общем, это линейные или слабонелинейные S-блоки размером 32x32, описанные простой комбинацией операций. Как их точно подбирали — непонятно.
Вот такие пироги. Напихали каких то констант, протолкнули свой алгоритм как стандарт и ничего никому не объяснили. И чем черт не шутит, может тот псевдопериод, который я нашел, позволяет дядькам из АНБ подделывать хэши как два пальца. А может и не позволяет.
Автор: Scratch






