Привет!

Эта статья станет вступительной в моем небольшом цикле заметок, посвященном такой технике анализа программ, как pointer analysis. Алгоритмы pointer analysis позволяют с заданной точностью определить на какие участки памяти переменная или некоторое выражение может указывать. Без знания информации об указателях анализ программ, активно использующих указатели (то есть программ на любом современном языке программирования — C, C++, C#, Java, Python и других), практически невозможен. Поэтому в любом мало-мальски оптимизируещем компиляторе или серьезном статическом анализаторе кода применяются техники pointer analysis для достижения точных результатов.
В данном цикле статей мы сосредоточимся на написании эффективного межпроцедурного алгоритма pointer analysis, рассмотрим основные современные подходы к задаче, ну и, конечно же, напишем свой очень серьезный алгоритм pointer analysis для замечательного языка внутреннего представления программ LLVM. Всех интересующихся прошу под кат, будем анализировать программы и многое другое!
Алгоритмы оптимизации и анализа программ
Представьте на секунду, что вы пишете компилятор для вашего любимого языка программирования. Позади написание лексических и синтаксических анализаторов, уже построено синтаксическое дерево модуля трансляции и исходная программа записана в терминах некоторого внутреннего представления (например, в виде байткода JVM или LLVM). Что дальше? Можно, например, попробовать интерпретировать полученное представление на некоторой виртуальной машине или транслировать это представление дальше, уже в машинный код. А можно сначала попробовать оптимизировать это представление, а потом уже заняться скучной трансляцией, верно? К тому же, программа будет работать быстрее!
Какие оптимизации мы можем применить? Рассмотрим, например, такой фрагмент кода.
k = 2;
if (complexComputationsOMG()) {
a = k + 2;
} else {
a = k * 2;
}
if (1 < a) {
callUrEx();
}
k = complexComputationsAgain();
print(a);
exit();
Обратите внимание на то, что переменная a принимает значение, равное 4, вне зависимости от того, какое значение вернула функция complexComputationsOMG, а это значит, что вызов этой функции из представления программы можно смело убрать (исходя из предположения, что все у нас функции чистые, в частности, не обладают побочными эффектами). Более того, раз в точке программы, в которой осуществляется сравнение переменной a с единицей, переменная a всегда принимает значение 4, то вызов callUrEx можно осуществлять безусловно, то есть избавиться от ненужного ветвления.
Кроме того, значение переменной k, присваемое в строчке k = complexComputationsAgain() нигде не используется, поэтому эту функцию можно и не вызывать! Вот что у нас получается после всех преобразований.
callUrEx();
print(4);
exit();
По-моему, неплохо! Все что нам осталось — научить наш оптимизатор осуществлять такие преобразования кода автоматически. Тут нам на помощь и приходит все многообразие алгоритмов dataflow analysis, и собственнолично очень крутой дядька Gary Kildall, который в своей монументальной рукописи «A unified approach to global program optimization» представил универсальный фреймворк для анализа программ, точнее так называемых dataflow problems.
Описательно, алгоритм итеративного решения dataflow problems, звучит очень просто. Все что нам нужно — определить набор свойств переменных, которые мы хотим отслеживать в процессе анализа (например, возможные значения переменных), функции интерпретации таких наборов для каждого базового блока и правила, по которым мы эти свойства будем распространять между базовыми блоками (например, пересечение множеств). В процессе итеративного алгоритма мы вычисляем значения этих свойств переменных в различных точках графа потока управления (Control Flow Graph, CFG), обычно в начале и конце каждого базового блока. Итеративно распространяя указанные свойства, мы должны в конечном итоге достигнуть неподвижной точки (fixpoint), в которой алгоритм заканчивает свою работу.

Разумеется, лучше один раз увидеть, чем сто раз услышать, поэтому подкрепим слова примером. Рассмотрим следующий фрагмент кода и попробуем отследить возможные значения переменных в различных точках программы.
b = 3;
y = 5;
while (...) {
y = b * 2;
}
if (b < 4) {
println("Here we go!");
}
Во врезке ниже решается классическая задача анализа программ, а именно — распространение констант (constant propagation) для рассматриваемого фрагмента кода.
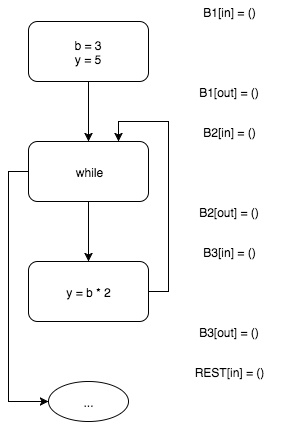
Интерпретируя входной блок B1, получаем, что на выходе этого блока b=3 и y=5. Функция f1 (аналогичные функции определяются для остальных блоков) — функция интерпретации блока.
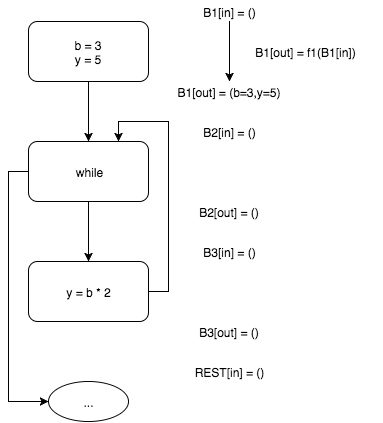
Блок входа в цикл в while B2 имеет двух предков — входной блок B1 и блок B3. Поскольку блок B3 пока не содержит возможных значений переменных, на текущем этапе алгоритма считаем, что на входе и выходе блока B2 b=3 и y=5. Функция U — правило распространения множеств свойств переменных (обычно — точная нижняя грань частично упорядоченного множества, а точнее — полной решетки).
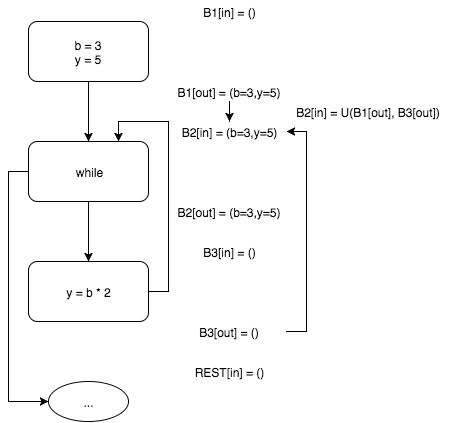
На выходе у базового блока B3 — b=3 и y=6.
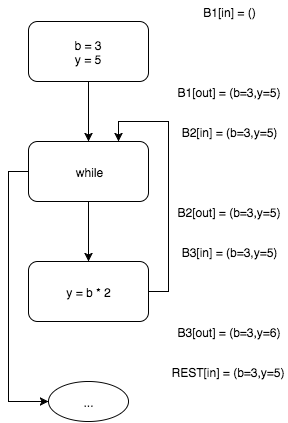
Поскольку информация о возможных значениях переменных была изменена (по сравнению с начальным состоянием, то есть как бы 0-й итерацией алгоритма), запускаем следующую итерацию алгоритма. Новая итерация повторяет предыдущую за исключением шага вычисления входного набора блока B2.
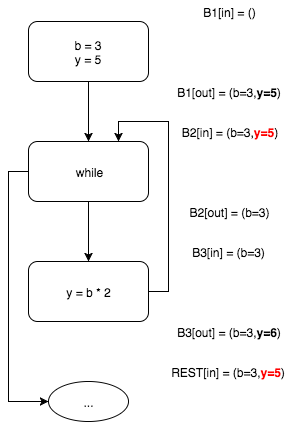
Как видим, на этот раз мы вынуждены как бы «пересечь» выходные наборы блоков B1 и B3. У этих наборов есть общая часть b=3 которую мы оставим и разнящиеся части y=5 и y=6, которые мы вынуждены отбросить.
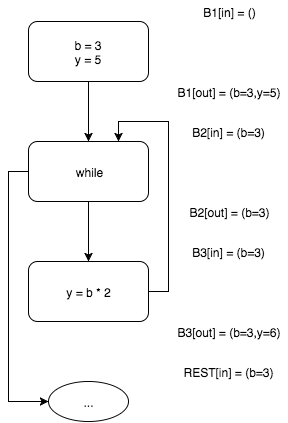
Поскольку продолжая вычисления далее мы не получаем никаких новых значений, работу алгоритма можно считать завершенной. Это и означает, что мы достигли неподвижной точки.
В своей работе Gary Kildall показал, что такой итеративный алгоритм всегда будет заканчивать свою работу и, более того, давать самый полный из возможных результатов, в случае если соблюдены следующие условия:
- домен отслеживаемых свойств переменных представляет собой полную решетку;
- функции интерпретации блока обладает свойством дистрибутивности на решетке;
- для «встречи» базовых блоков-предшедственников используется оператор точной нижней грани (то есть функция meet частично упорядоченного множества).
Таким образом, для оптимизации программ мы можем применять всю мощь алгоритмов dataflow analysis, используя, например, итеративный алгоритм. Возвращаясь к нашему первому примеру, мы использовали constant propagation и liveness analysis (live variable analysis) для осуществления оптимизации dead code elimination.
Более того, алгоритмы dataflow analysis могут использоваться при осуществлении статического анализа кода в контексте информационной безопасности. Например, в процессе поиска уязвимостей класса SQL-injection, мы можем отмечать специальным флагом все переменные, на которые каким-либо образом может повлиять злоумышленник (например, параметры HTTP-запроса и т.п.). Если окажется, что переменная, помеченная таким флагом, участвует в формировании SQL-запроса без надлежащей обработки — мы, скорее всего, нашли серьезную дыру в безопасности приложения! Останется лишь показать сообщение о возможной уязвимости и красиво уйти в горизонт предоставить пользователю рекомендации по диагностике и устранению такой уязвимости.
Умножаем скорбь
Иван кивает на Петра, а Петр на Ивана
Подводя итоги предыдущего пункта, алгоритмы dataflow analysis — хлеб насущный (и масло!) любого компиляторщика. Так причем здесь, собственно, pointer analysis, и зачем он, собственно, нужен?
Спешу испортить вам настроение следующим примером.
x = 1;
*p = 3;
if (x < 3) {
killTheCat();
}
Вполне очевидно, что не зная, куда указывает переменная p, мы не можем с уверенностью заявить, чему будет равняться значение выражения x < 3 в условном операторе if. Ответ на этот вопрос мы можем дать лишь выяснив контекст, в котором данный фрагмент кода появляется. Например, p может быть глобальной переменной из другого модуля (которая в языках программирования семейства C может указывать на что угодно и когда угодно) или локальной переменной, указывающей куда-то в кучу. Даже зная контекст, нам все еще необходимо знать множество локаций (абстрактных ячеек памяти), на которые эта переменная может указывать. Если, например, перед указанным фрагментом кода переменная p инициализировалась как p = new int, тогда мы должны удалить из оптимизированной программы условный переход и вызвать метод killTheCat безусловно.
Раз так, ни одной оптимизации мы применить к этому коду не сможем, пока не найдем какой-либо способ раз и навсегда выяснить, куда могут указывать переменные в анализируемой программе!
Думаю, сейчас уже стало очевидным, что без применения алгоритмов pointer analysis нам не обойтись (и по какой причине вообще возникла необходимость решать эту сложную, а точнее, алгоритмически неразрешимую задачу). Pointer analysis — это метод статического анализа кода, который определяет информацию о значениях указателей или выражений, имеющих тип указатель. В зависимости от решаемых задач, pointer analysis может определять информацию для каждой точки программы или для программы целиком (flow-sensitivity) или в зависимости от контекста вызова функции (context-sensitivity). Более подробно о типах pointer analysis я расскажу в одной из следующих статей цикла.
Результат анализа обычно представляется в виде отображения из множества указателей во множество наборов локаций, на которые эти указатели могут ссылаться. То есть, проще говоря, каждому указателю p сопоставляется множество объектов, на которые он может указывать. Например, во фрагменте кода, приведенном ниже, результатом анализа будет отображение p -> {a, b}, q -> {p}.
int a, b, c, *p, **q;
p = &a;
q = &p;
*q = &b;
Важно отметить, что отображение, вычисляемое pointer analysis, должно отвечать критерию безопасности, то есть быть максимально консервативным. В противном случае, мы можем просто испортить семантику исходной программы своими оптимизациями. Например, безопасным приближением результата pointer analysis для фрагмента программы выше, может быть p -> {a, b, c}, q -> {unknown}. Значение unknown используется для того, чтобы показать, что указатель может ссылаться на все доступные объекты программы.
Например, в рассматриваемом ниже фрагменте кода, разыменование переменной p потенциально может изменить значение любого объекта программы!
extern int *offensiveFoo();
p = offensiveFoo();
*p = 77;
Мы ничего не знаем про функцию offensiveFoo, поскольку она была импортирована из другого модуля трансляции, а потому вынуждены предположить, что p может указывать совершенно на что угодно!
В дальнейшем будем считать, что все рассматриваемые функции и глобальные переменные принадлежат анализируемому модулю трансляции, за исключением случаев, когда обратное явно обговорено словами.
Poor Man's Pointer Analysis

Впервые столкнувшись с проблемой алиасинга указателей, я, не долго думая, решил попробовать решить задачу используя уже известный итеративный алгоритм на решетке (тогда я и понятия не имел, что решаю задачу ту же задачу, что и решают алгоритмы pointer analysis). Действительно, что нам мешает отслеживать объекты, на которые могут ссылаться указатели как набор свойств этих указателей? Давайте попробуем отследить работу алгоритма на простом примере. Правила распространения множеств объектов пусть соответствуют «естественной» семантике программы (например, если p = &a, то p -> {a}), а распространять эти наборы между базовыми блоками мы будем простым объединением множеств (например, если q -> {a, b} и q -> {c} подаются на вход некоторому базовому блоку, то входным набором для такого блока будет q -> {a, b, c}).
Рассмотрим работу алгоритма на простом примере.
x = &a;
a = &z;
if (...) {
x = &b;
} else {
c = &x;
}
Дождемся пока итеративный алгоритм закончит работу и посмотрим на результаты.
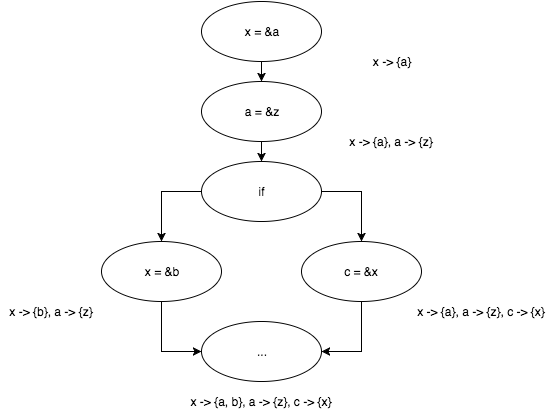
Работает! Не смотря на простоту алгоритма, представленный подход имеет право на жизнь. Скажу больше, именно так (разумеется, со значительными улучшениями) решали задачу алиасинга указателей до появления работы Андерсена «Program Analysis and Specialization for the C Programming Language». Кстати, именно этой работе и будет посвящена следующая статья цикла!
Основные недостатки описанного подхода — плохая масштабируемость и слишком консервативные результаты, поскольку при анализе реальных программ нужно обязательно учитывать вызовы других функций (то есть анализ должен быть межпроцедурным) и, зачастую, контекст вызова функции. Существенный же плюс такого подхода в том, что информация об указателях доступна для каждой точки программы (то есть алгоритм flow-sensitive), тогда как алгоритмы Андерсена и его последователей вычисляют результат для программы целиком (flow-insensitive).
Вместо заключения

На этом завершается первый кусочек моего цикла заметок об алгоритмах pointer analysis. В следующий раз напишем простой и эффективный межпроцедурный pointer analysis алгоритм для LLVM!
Всем большое спасибо за уделенное статье время!
Автор: Solar Security






