Продолжаем разбирать задания online-этапа NeoQUEST-2016 и готовимся к "очной ставке", куда приглашаем всех желающих! Вас ждут интересные доклады, демонстрации атак, конкурсы, призы и многое другое!
Продолжаем разбирать задания online-этапа NeoQUEST-2016 и готовимся к "очной ставке", куда приглашаем всех желающих! Вас ждут интересные доклады, демонстрации атак, конкурсы, призы и многое другое!
Редкий хак-квест обходится без криптографии, ну и NeoQUEST-2016 не стал исключением! В задании online-этапа наш выбор пал на криптосистему RSA, о безопасности которой можно говорить много и долго. В образовательно-познавательных целях, мы взяли не самую популярную атаку на RSA – атаку Хастада.
Кроме этого, мы порядком запутали участников, не предоставив им (на первый взгляд!) никаких исходных данных к заданию. О том, где нужно было искать, что делать с найденным и как реализовать атаку Хастада – читаем под катом!
А где задание?
… с таким вопросом обращались на support@neoquest.ru наши участники. Их можно было понять: тексты обеих легенд толком не говорили ничего.
После прозрачных намеков участники вспоминали о карте на главной странице сайта и шли изучать ее.
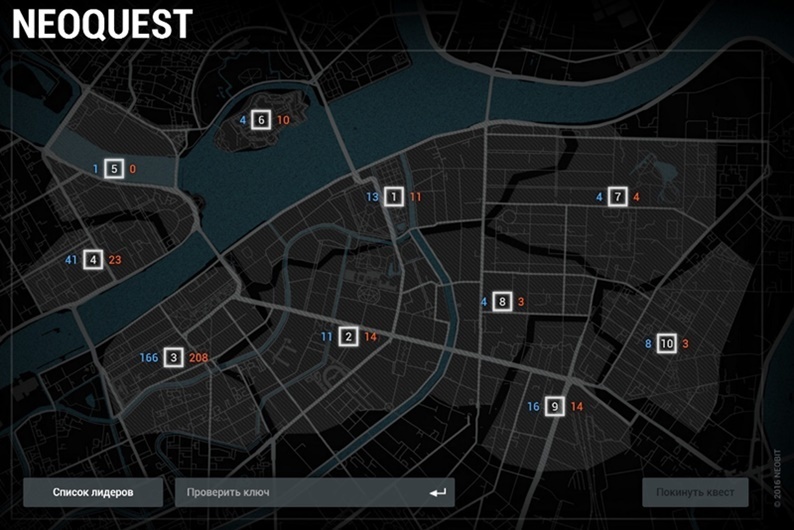
Найти исходные данные для задания можно было несколькими путями. Очень внимательные везунчики замечали, что если поводить по карте курсором мышки, то в некоторых точках (а точнее, в трёх!) курсор меняется на руку, которая обычно появляется при наведении на ссылку. По клику скачивался файл формата .asn1.
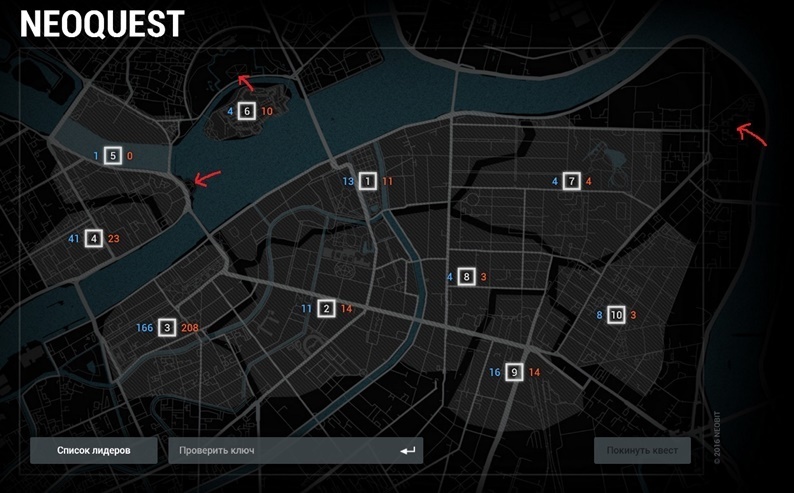
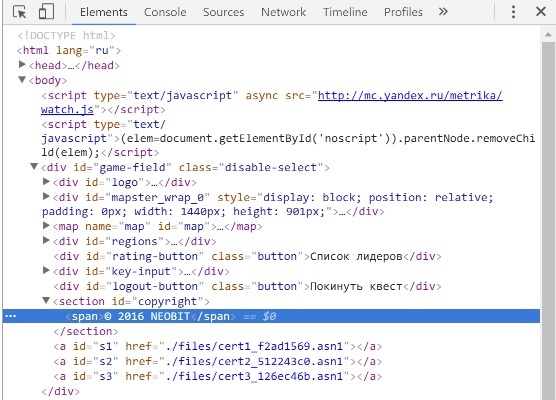
Другие участники решили не напрягать глаза и просматривали сайт «инспектором», и вскоре где-то под копирайтом обнаруживали те самые три спрятанные файла: cert1_f2ad1569.asn1, cert2_512243c0.asn1, cert3_126ec46b.asn1.
Парсим ASN.1
ASN.1 представляет собой стандарт кодирования информации, широко используемый, в том числе, в криптографии. Подробнее почитать о стандарте можно как на Хабре (детальная, написанная понятным языком статья), так и на сторонних ресурсах (тут и там). Любые данные в ASN.1 представляются в виде последовательности «Тэг – Длина – Значение». При этом «Тэг» определяет тип данных, а «Длина» задает размер следующего поля «Значение».
Для того, чтобы узнать, что же за информация находится в этих трех .asn1 файлах, их нужно распарсить. Для этого существует множество программ, например, ASN.1 JavaScript decoder или приложение командной строки dumpasn1.
Используем dumpasn1, открыв в нем по очереди все три файла, видим следующее:
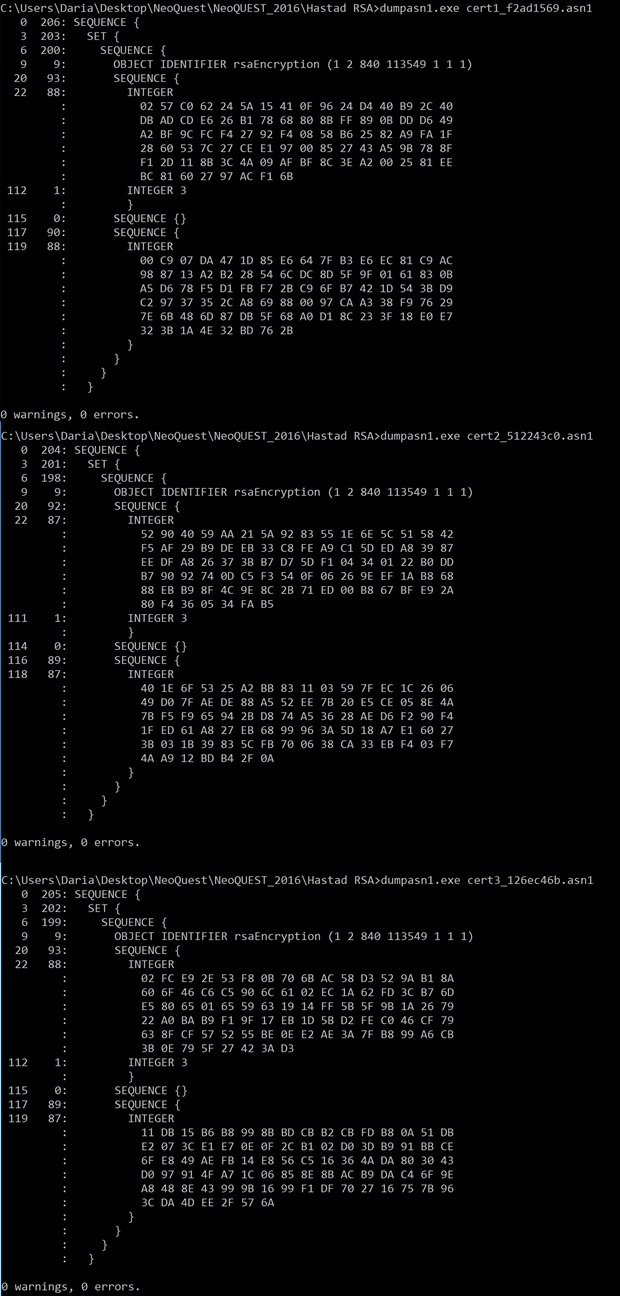
Структура всех трех файлов одинакова, строка OBJECT IDENTIFIER rsaEncryption во всех трех файлах ясно указывает на RSA. Каждый файл содержит, по-видимому, по 3 параметра RSA, и один параметр у всех трех файлов одинаковый и равный 3. Начинаем изучать возможные атаки на RSA (например, на Вики), и параметр 3, заметно маленький по сравнению с двумя другими параметрами, наталкивает на мысль о том, что это — ни что иное, как открытая экспонента e! А значит, можно реализовать атаку Хастада.
Реализуем атаку Хастада
Исходные данные к атаке
Подробно прочитать про атаку Хастада можно здесь. Условия для реализации атаки следующие: пользователь А отсылает зашифрованное сообщение m нескольким пользователям. в данном случае, трём (по числу файлов): P1, P2, P3. У каждого пользователя есть свой ключ, представляемый парой «модуль-открытая экспонента» (ni, ei), причём M < n1, n2, n3. Для каждого из трех пользователей А зашифровывает сообщение на соответствующем открытом ключе и отсылает результат адресату.
Атакующий же реализует перехват сообщений и собирает переданные шифртексты (обозначим их как C1, C2, C3), с целью восстановить исходное сообщение M. Внимательно смотрим на наши .asn1 файлы: первый параметр, очевидно, модуль RSA n, второй, как мы уже выяснили — открытая экспонента, а значит, третий параметр и есть шифртекст. Значит, по имеющимся трем шифртекстам нужно восстановить сообщение, которое либо будет ключом. либо даст подсказку к тому, где искать ключ к заданию.
Почему точно сможем ее реализовать?
Как известно, шифрование сообщения по схеме RSA происходит следующим образом: C = Me mod n. В случае с открытой экспонентой, равной 3, получение шифртекстов выглядит так:
C1 = M3 mod n1
C2 = M3 mod n2
C3 = M3 mod n3
Зная, что n1, n2, n3 взаимно просты, можем применить к шифртекстам китайскую теорему об остатках.
Получим в итоге некоторое C', корень кубический из которого и даст нам искомое сообщение M!
C' = M3 mod n1n2n13
Вспоминаем, что M меньше каждого из трёх модулей ni, значит, справедливо равенство:
C' = M3
Так мы и найдем наше искомое сообщение M.
Программная реализация атаки Хастада
Один из наших участников реализовал скрипт на Python, его подробный writeup лежит тут, мы же приведем только код скрипта оттуда:
import math
c_flag1 = 258166178649724503599487742934802526287669691117141193813325965154020153722514921601647187648221919500612597559946901707669147251080002815987547531468665467566717005154808254718275802205355468913739057891997227
N1=770208589881542620069464504676753940863383387375206105769618980879024439269509554947844785478530186900134626128158103023729084548188699148790609927825292033592633940440572111772824335381678715673885064259498347
c_flag2 = 82342298625679176036356883676775402119977430710726682485896193234656155980362739001985197966750770180888029807855818454089816725548543443170829318551678199285146042967925331334056196451472012024481821115035402
N2=106029085775257663206752546375038215862082305275547745288123714455124823687650121623933685907396184977471397594827179834728616028018749658416501123200018793097004318016219287128691152925005220998650615458757301
c_flag3 = 22930648200320670438709812150490964905599922007583385162042233495430878700029124482085825428033535726942144974904739350649202042807155611342972937745074828452371571955451553963306102347454278380033279926425450
N3=982308372262755389818559610780064346354778261071556063666893379698883592369924570665565343844555904810263378627630061263713965527697379617881447335759744375543004650980257156437858044538492769168139674955430611
def chinese_remainder(n, a):
sum = 0
prod = reduce(lambda a, b: a*b, n)
for n_i, a_i in zip(n, a):
p = prod / n_i
sum += a_i * mul_inv(p, n_i) * p
return sum % prod
def mul_inv(a, b):
b0 = b
x0, x1 = 0, 1
if b == 1: return 1
while a > 1:
q = a / b
a, b = b, a%b
x0, x1 = x1 - q * x0, x0
if x1 < 0: x1 += b0
return x1
def find_invpow(x,n):
"""Finds the integer component of the n'th root of x,
an integer such that y ** n <= x < (y + 1) ** n.
"""
high = 1
while high ** n < x:
high *= 2
low = high/2
while low < high:
mid = (low + high) // 2
if low < mid and mid**n < x:
low = mid
elif high > mid and mid**n > x:
high = mid
else:
return mid
return mid + 1
flag_cubed = chinese_remainder( [N1, N2, N3], [c_flag1, c_flag2, c_flag3] )
flag=find_invpow(flag_cubed,3)
print hex(flag)[ 2 : -1 ].decode("hex")
Как видно из кода, сначала из файлов были получены параметры ni и Ci, которые из HEX-формата были трансформированы в целые большие числа. Затем была реализована китайская теорема об остатках и, наконец, извлечен кубический корень — для получения искомого сообщения.
key=bff149a0b87f5b0e00d9dd364e9ddaa0
Полученное сообщение содержит в себе ключ, задание пройдено!
В заключение
В продолжение к заданиям NeoQUEST прошлых лет, где участникам требовалось найти ошибку в реализации схемы RSA или провести атаку разложения модуля (разбор задания здесь), реализовать атаку Винера , была выбрана атака Хастада, не основанная на разложении на множители.
Как показала статистика обращения участников online-этапа NeoQUEST-2016 в support, основную проблему для них представила непонятная формулировка задания и спрятанные исходные данные. Однако формат файлов также поставил в тупик некоторых участников.
Лучшие участники online-этапа уже совсем скоро встретятся на «очной ставке» 7 июля в Санкт-Петербурге! А мы приглашаем всех — специалистов ИБ-фирм, хакеров и гиков, абитуриентов и студентов IT-специальностей — отлично провести время, слушая доклады и участвуя в конкурсах, пока ребята-участники в поте лица проходят задания! Вход свободный, нужна только регистрация на сайте. NeoQUEST — еще одна причина посетить Питер этим летом!
Автор: НеоБИТ