Продолжим серию статей «ИИ для чайников». Если в прошлой статье мы попробовали отграничить людей, решающих задачи «оракулов сильного ИИ» от задач «слабого ИИ», и показать решение какого рода задач дает больше, чем лирические «откровения». Одну из таких задач мы назвали «задача двух учителей».
То теперь мы посмотрим на неё под другим углом зрения. Как я говорил эта задача встречается в разных аспектах. А заодно мы посмотрим как глубоко заблуждаются инженеры «слабого ИИ» в текущей тенденции понимания задач ИИ. К сожалению, теперь образование в этой области поощряет создавать убогие формализмы и зауживать взгляд на проблематику ИИ. С одним из «выкидышей» такого рода образования мы и дискутировали в прошлой статье. Но таких людей много и напрягает тенденция при «штамповке» такого рода «образованных студентов».
Суть задачи адаптации
Тут я попробую пересказать основы. Они взяты из монографии Л. А. Растригин «Адаптация сложных систем».
Разъяснение понятия адаптации как приспособления к новым условиям, которое вполне удовлетворяет биологов и социологов, совершенно неудовлетворительно с точки зрения инженера.
Понятие адаптации можно разделить на два вида (в действительности оба вида адаптации встречаются одновременно и взаимодействуют друг с другом):
Пассивная адаптация — приспособление к фиксированной среде. Адаптирующаяся система функционирует так, чтобы выполнять свои функции в данной среде наилучшим образом, т. е. максимизирует свой критерий эффективности функционирования в данной среде. Пример пассивной адаптации можно наблюдать у растений.
Активная адаптация — поиск среды, адекватной данной системе. При этом подразумевается либо изменение среды с целью максимизации критерия эффективности, либо активный поиск такой среды, в которой достижим желаемый комфорт. Пример активной адаптации можно наблюдать у животных.
Чем замечательна работа Растригина, тем что он математически ввел понятие субъекта, в то время как все остальные говорят лишь о задачах так сказать объективных. А соответственно, раз у них нет математического понятия субъекта — соответственно все эти теории далеки от ИИ. Точнее отсутствие математического понятия субъекта позволяет говорить только в рамках слабого ИИ. Имея философское, психологическое понятие ИИ — еще хуже — проблема «оракулов сильного ИИ».
Для наших целей, нет необходимости разбираться что такое субъект математически. Главное, что такое понятие есть и оно позволяет выделить разные уровни адаптации, которые применимы к: (1) формулировке целей управления, (2) определении объекта управления, (3) структурном синтезе модели (4) параметрическом синтезе модели.
Современное состояние науки ИИ заключается в том, что автоматически мы умеем осуществлять только параметрический синтез модели, и соответственно, автоматически происходит только параметрическая адаптация.
О первых двух уровнях (целях управления и определении объекта управления) мы вообще говорить не будем, т.к. нет даже близко понимания того, как это осуществлять. Нам достаточно рассмотреть хотя бы разницу между структурной и параметрической адаптацией.
Параметрическая и структурная адаптация
Параметрическая адаптация связана с коррекцией, подстройкой параметров модели. Необходимость в такого рода адаптации возникает ввиду дрейфа характеристик управляемого объекта. Адаптация позволяет подстраивать модель на каждом шаге управления, причем исходной информацией для нее является рассогласование откликов объекта и модели, устранение которого и реализует процесс адаптации.
Адаптивное управление, в процессе которого не только достигаются цели, но и уточняется модель, называют дуальным. Здесь путем специальной организации управления сразу достигаются две цели — управления и адаптации модели.
Именно о таком роде адаптации мы говорили в статье Резюме проблемы «двух и более учителей» и субъективное мнение о ИИ-сообществе, когда разбирались как и зачем задавать функцию пригодности с помощью искусственной нейронной сети.
Чем же отличается структурная адаптация?
Любая модель F состоит из структуры и параметров: F = ‹St, C›, где St — структура модели F, C = (C_1, ..., C_k) — ее параметры.
Далеко не всегда адаптация модели путем коррекции ее параметров позволяет получить адекватную модель объекта. Неадекватность возникает при несовпадении структур модели и объекта. Если в процессе эволюции объекта его структура изменяется, то такая ситуация складывается постоянно.
Горькая пилюля на субъективном примере
Современных ИИ-инженеров учат осуществлять структурную адаптацию самим — т.е. выполнять работу за машину. Причем это происходит с таким самопожертвованием и себялюбием, что они даже не понимают что они делают. Вот характерные фразы (лулзы), которые можно тут словить:
1. Для решения вашей задачи не нужно ничего, кроме него.
2. Зачем вам скрытый слой, если с этой задачей справляется один нейрон?
3. Я умею решать задачи и выбираю под них подходящий инструмент, вместо «универсального решателя».
Имеем классическое начало — человек не понимает задачи необходимости структурной адаптации. С помощью своих знаний пытается сам решить задачу «синтеза структуры модели». При этом отвергает необходимость научить этому машину. И все заканчивается абсолютно феерично — объявляет себя «умным», а остальных «дураками» только потому, что он якобы умеет выбирать «подходящий инструмент».
Нет это не «выбор инструмента», увы, это текущие кредо современных ИИ-инженеров, которые остановились в своем развитии и не видят интеллектуальной задачи в том, что они делают за машину. Это такие ИИ-инженеры которые с гордостью будут только и делать, что толкаться на ступенях нашей пирамиды, и мешать другим идти по направлению к беседке на вершине пирамиды.
Отношение у меня лично к таким ИИ-инженерам ровно такое же как и к оракулам сильного ИИ, и меня даже иногда радует, когда оракулы сильного ИИ за дело критикуют такого рода ИИ-инженеров. Ибо не ведают что творят, и в чем состоит их задача как спецмалистов в области ИИ.
Немного о «чистом обобщении»
Розенблатт так сформулировал понятие чистого обобщения:
Модели предъявляются N различных стимулов и требуется, чтобы она реагировала на них различным образом. Вначале проводится обучение во время которого модели предъявляется некоторая последовательность образов, в которую входят представители каждого из классов, подлежащих различению. Затем предъявляется контрольный стимул и определяется вероятность получения правильной реакции для стимулов данного класса.
Если контрольный стимул не совпадает ни с одним из обучающих стимулов, то эксперимент связан не только с «чистым различением», но включает в себя элементы «обобщения». Если контрольный стимул возбуждает некоторый набор сенсорных элементов, совершенно отличных от тех элементов, которые активизировались при воздействии ранее предъявленных стимулов того же класса, то эксперимент является исследованием «чистого обобщения».
Почему сейчас эти задачи не решаются ни представителями сильного ИИ, не представителями слабого ИИ? У меня есть лишь один ответ: первые не понимают суть подобных экспериментов, вторые не понимают значимость таких экспериментов. И в итоге мы топчемся на месте.
Вот посмотрим в этом разрезе на то как мы решали задачу сложения в статье Резюме проблемы «двух и более учителей» и субъективное мнение о ИИ-сообществе.
Когда мы указали, что имеем 256 выходов, а обучающая выборка это лишь половина возможных вариаций, то оказывается:
* Нарушается следующие положение: проводится обучение во время которого модели предъявляется некоторая последовательность образов, в которую входят представители каждого из классов, подлежащих различению
* Мы показали перцептрону только как получаются нечетные числа. Он понятия не имел о том, что существуют в природе четные числа. Весовые коэффициенты после обучения к четным числам были нули. Именно поэтому там такой плохой прогноз. Но все равно перцептрон сделал кое какой прогноз, несмотря на то что он не мог знать о существовании четных чисел. Он попробовал без какой-либо классификации, лишь на основании вида слагаемых в двоичном представлении — в том месте, где должно было быть четное число дать хоть какое-то известное ему нечетное число, но такое что оно близко к четному. По сути о выполнил «наивную» кластеризацию.
* Поэтому сравнивать результаты прогноза как это сделал ererer с алгоритмом MLP+BackProp тут не релевантно
* Т.е. перцептрон решал задачу как задачу с элементами «обобщения», а MLP+BackProp знал о задаче слишком много — он решал задачу аппроксимации. Перцептрону же не было дано такое структурное знание (помним о структурной адаптации?) какого рода эта задача. И по сути перцептрон просто физически не мог тут обобщать.
Изменим немного условия задачи
Попробуем следующим шагом немного изменить условия задачи, чтобы перцептрон имел бы основания для обобщения. Вначале уменьшим размерность задачи с 64х64 до 32х32, это не повлияет на выводы, но зато рассчитывается быстро.
Теперь наша функция будет не c= a + b, в которой существует выше описанная особенность, что научившись на нечетных числах, нет возможности вывести наличие четных чисел.
Теперь мы возьмем функцию c= (int) (a + b)/4 с округлением до целого числа. Визуально это выглядит так (чтобы отличать задачи возьмем на этот раз в градации зеленного):

(слева полная функция, справа обучающие точки для перцептрона)
Теперь давайте проанализируем, как исследуемая нами функция c= (int) (a + b)/4 способствует прогнозу. Понятно, что чем больше примеров образов на каждый класс тем прогноз будет лучше. Это можно отобразить следующим квадратом:

Синие квадратики это точки о которых перцептрон ничего не знает и их надо ему спрогнозировать. Но рядом ему известны зеленные, чем зеленый более яркий тем больше примеров ему известно. В крайних углах известно всего по одной точке, а в центральной диагонали 62 примера. Соответственно, ожидать, что перцептрон будет равномерно обобщать эту функцию — не приходится. Его качество прогноза будет зависеть от вида прогнозируемой функции.
И будет таким:
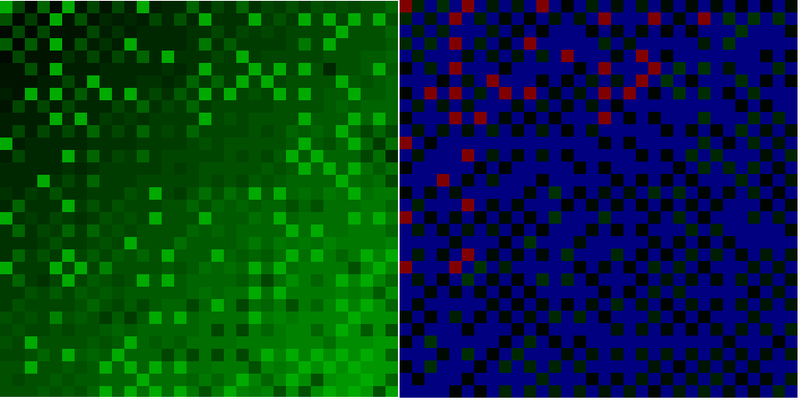
Слева полная карта прогноза, справа распределение величины ошибки (синие точки — отсутствие ошибки, градации от черного до зеленого — ошибка до 10 единиц, красные ошибка выше 10 единиц). Или распределение ошибок в цифрах:
Величина ошибки = Число соответствующих точек
0 = 631
1 = 114
2 = 63
3 = 23
4 = 45
5 = 25
6 = 28
7 = 19
8 = 19
9 = 10
10 = 14
11 = 9
12 = 4
13 = 8
14 = 6
15 = 3
16 = 2
17 = 1
Это немного хуже, чем при MLP+BackProp, но разница в том, что перцептрон исходит только из статистики появления образов, а при применении MLP+BackProp экспериментатором выполняется дополнительно задача структурной адаптации.
Теперь если бы мы научились осуществлять структурную адаптацию, то и перцептрон смог бы прогнозировать не только на основании статистики обучающей выборки, но и учитывая структуру / вид функции.
Автор: tac

