Сфера Блоха для бройлеров

В этой публикации мы попробуем подробно разобрать, что же такое сфера Блоха, иллюстрирующая пространство состояний одного двухуровневой квантовой системы, что в области квантовых вычислений зовётся "кубитом". Для тех, кто желает понять, зачем на математике мучают бесполезными комплексными числами, узреть одно из красивейших применений комплексных чисел и сферической системы координат.

Центральной идеей квантовых компьютеров является переход от использования кодировки информации в виде последовательности битов, которые могут принимать значения 0 и 1, к последовательностям кубитов. Каждый кубит -- это двухуровневая квантовая система (далее мы будем использовать эти определения как эквивалентные понятия): у нас есть состояние |0⟩, являющееся аналогом 0 бита, и состояние |1⟩, аналог 1 бита. Вариантов того, что из себя могут представлять |0⟩ и |1⟩, очень много: спины |0⟩ = |↑⟩, |1⟩= |↓⟩ ("вверх"/"вниз"), состояния ангармонического осциллятора, поляризации фотонов (см. подробнее, например, здесь). Но в квантовой механике, согласно принципу суперпозиции, все подобные кубиты описываются при помощи волновой функции, вектора состояния |ψ⟩:

Поскольку наша система по нашему же предположению, имеет только два возможных состояния для финального измерения, то получается, что состояние описывается двумерным вектором комплексных коэффициентов перед состояниями c₀ и c₁, т.е. (c₀,c₁)^T, а наши состояния |0⟩ и |1⟩ являются базисными векторами, причём перпендикулярными друг другу, записывается это как

Но не всё так просто с этим выражением, по своему смыслу, коэффициенты c₀ и c₁ связаны с вероятностью обнаружить кубит в состоянии |0⟩ или |1⟩, обозначим их p₀ и p₁:

Мы, конечно, можем позволить себе выбирать эти коэффициенты какими угодно, но физически значимыми являются т.н. нормированные коэффициенты, такие что

Т.е. полная вероятность найти систему в состоянии |ψ⟩ равна единице, в этом случае квадрат модуля каждого из коэффициентов -- это просто вероятность найти кубит в соответствующем базисном состоянии |n⟩ (p_n=|c_n|², n=0,1). Выражение |c₀|²+|c₁|²=1 можно легко параметризовать при помощи основного тригонометрического тождества:

Любое комплексное число z=a+b·i можно представить в показательной форме:

где A=|z|≥0 -- это модуль комплексного числа, а φ -- фаза z, вычисляемая через преобразование в полярные координаты:

Отсюда видно, что модули коэффициентов c₀ и c₁ должны быть неотрицательными. Исходя из основного тригонометрического тождества, мы можем определить коэффициенты волновой функции |ψ⟩ как

При такой параметризации, из условия |c_n|≥0, у нас получается, что угол θ может меняться от 0 до π, и мы выбираем это, осознанно, чтобы этот угол был похож на полярный азимутальный угол в сферических координатах, собственно, для этого и нужна двойка в θ/2. Но на самом деле для этого есть и более физические предпосылки

И, само, собой, используя показательную форму комплексных чисел, мы можем представить коэффициенты волновой функции в виде:

Где по смыслу углы φ_n -- это полярные углы. Вроде всё хорошо, но у нас оказывается, что состояние |ψ⟩ определяют три числа: азимутальный угол (θ) и два полярных (φ₀ и φ₁). Но возникает резонный вопрос: а все ли они нужны, и ответ, как все уже догадались, нет.

В квантовой механике нас интересуют наблюдаемые величины, а представляются они в виде операторов, например, если у нас есть величина O от слова "observable", то её оператор обозначается добавлением сверху крышечки. В случае двухуровневой системы, оператор -- это по-сути, матрица, действующая на вектор коэффициентов (c₀,c₁)^T, и превращающая его в вектор новых коэффициентов:

причём ⟨0|O|1⟩=⟨1|O|0⟩* звёздочка обозначает комплексное сопряжение. Для нас важно, что среднее значение любой произвольной наблюдаемой для заданного состояния было бы одним и тем же числом, т.е. если

то мы разницы между состояниями |ψ⟩ и |ψ'⟩ не увидим: для нас они будут наблюдаемо одним и тем же состоянием. Теперь предположим, что |ψ'⟩=e^iφ·|ψ⟩, тогда ⟨ψ'|=e^-iφ·⟨ψ|, а значит

т.е. фаза всего состояния даёт нам то же самое наблюдаемое состояние. Поэтому мы можем переписать наше двухуровневое состояние

как

Соответственно, исходя из вышесказанного, можно спокойно проигнорить множитель e^iφ0, и тогда единственным полярным углом, который у нас останется, будет разность фаз φ=φ₁-φ₀, и только сий угол определяет наше квантовое состояние.

В сухом остатке, наше состояние |ψ⟩ имеет вид:

и параметризуется двумя параметрами:

• углом φ в интервале от 0 до 2π имеющим смысл разности фаз между двумя двумя базисными состояниями,

• углом θ, от 0 до π, задающим относительное "содержание" базисных состояний |0⟩ и |1⟩ в нашей волновой функции |ψ⟩.

Но вся наша конструкция очень подозрительно напоминает сферические координаты, которые, традиционно, задаются следующим образом:

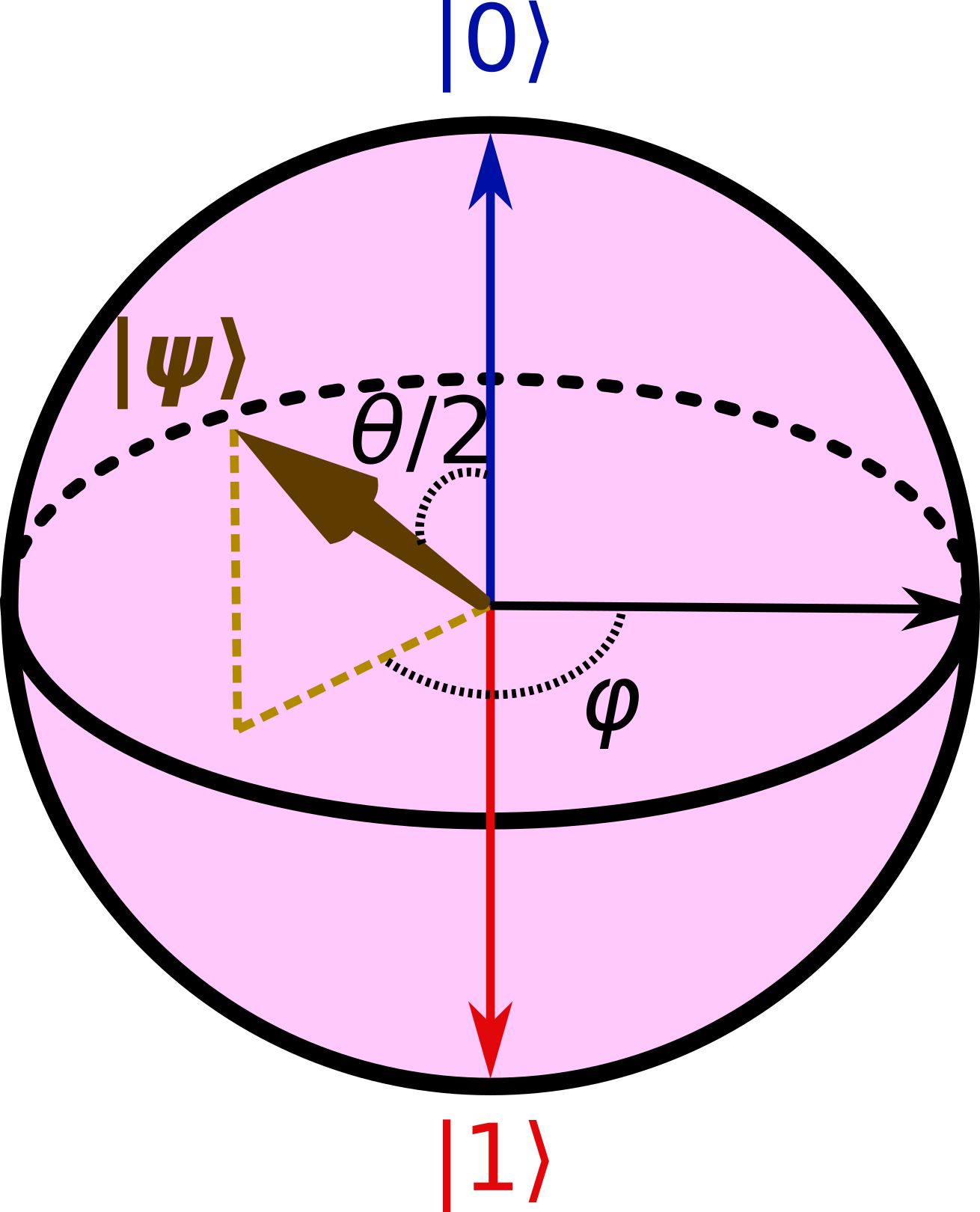
где r -- радиус, φ -- полярный угол (от 0 до 2π), а θ -- азимутальный угол (от 0 до π). Если мы зафиксируем радиус, то изменение углов опишет нам сферу в трёхмерном пространстве, а поскольку углы определены точно так же, как и для нашей волновой функции для двухуровневой системы, то мы можем отобразить все возможные состояния, как точки на сфере фиксированного радиуса r, и такое представление состояний двухуровневой системы зовётся сферой Блоха, в честь Нобелевского лауреата по физике Феликса Блоха.

Разберёмся как эта сфера устроена (см. рисунок в самом начале статьи), разобрав, какие вектора (x,y,z)^T в трёхмерном пространстве соответствуют каким состояниям |ψ⟩.

• При θ=0 (и любом значении φ) мы получим состояние |ψ⟩=|0⟩, это будет соответствовать вектору (0,0,r)^T, это верхняя точка сферы, её "северный полюс".

• Напротив "северного полюса" будет южный полюс (0,0,-r)^T, при θ=π (и любом значении φ), это соответствует состоянию |ψ⟩=|1⟩. В этом смысле, наши базисные состояния -- это уникальные противоположности.

• При θ=π/2 и каком-то значении φ, мы окажемся на экваторе (z=0, x²+y²=r²), когда в нашем состоянии |ψ⟩ ровно 50/50 вкладов от состояний |0⟩ и |1⟩.

• Соответственно, в "северном полушарии" (выше экватора, при z>0) у нас будет больше |0⟩ в состоянии |ψ⟩, а в "южном полушарии" (ниже экватора, при z<0), наоборот, больше |1⟩.

Вот таким вот нехитрым способом можно легко и просто визуально изображать всякие весёлости, происходящие с состоянием двухуровневой системы. Конечно, физический смысл этого изображения существенно богаче: например, для частиц со спином 1/2 эта сфера будет давать пространственное направление спина, но это уже отдельный интересный вопрос.