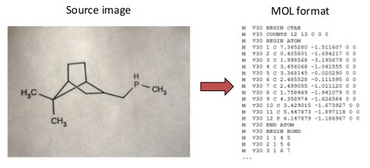
В настоящей заметке я расскажу о том, как можно построить систему оптического распознавания структурной информации, опираясь на алгоритмы, применяющиеся в обработке изображений и их реализации в рамках библиотеки OpenCV. За описанием системы стоит активно развивающийся open source проект Imago OCR, который может быть непосредственно полезен в распознавании химических структур, однако в заметке я не буду говорить о химии, а затрону более общие вопросы, решение которых поможет в распознавании структурированной информации различного рода, например таблицы или графики.
Структура движка распознавания
Одним из самых общих вариантов изображения структуры движка системы оптического распознавания можно выбрать следующий:
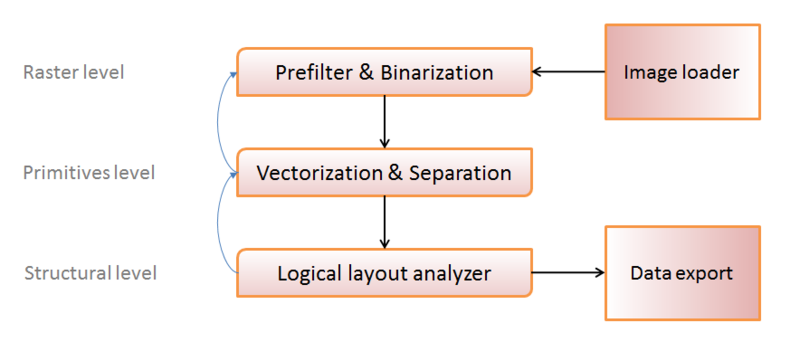
Условно методы обработки можно поделить на три уровня:
- Уровень растра (работаем с набором пикселей изображения);
- Уровень примитивов (отождествляем группы пикселей с определенными примитивами, — символами, линиями, окружностями и т.п.);
- Структурный уровень (собираем группы примитивов в логические единицы — «таблица», «ячейка таблицы», «метка» и т.п.)
Черными стрелками я изобразил основное направление передачи данных: загружаем изображение, преобразуем в удобный для обработки вид, получаем примитивы, организуем примитивы в структуры, записываем результат.
Голубые стрелки изображают «обратную связь» — в ряде случаев распознать объект на определенном уровне становится невозможно (собрать из примитивов хоть какую-то логически допустимую структуру, или же из набора точек вычленить хоть какой-либо примитив). Это свидетельствует либо о «плохом» исходном изображении, либо же об ошибке на предыдущем шаге, и чтобы избежать подобных ошибок, мы пробуем обработать объект заново, возможно с другими параметрами, на предыдущем структурном уровне.
На данном этапе мы не будем углубляться в детали, но этим системы оптического распознавания структурной информации существенно отличаются от «общего распознавания», — у нас есть возможность скорректировать некоторые ошибки благодаря пониманию необходимой выходной структуры. Это обстоятельство несколько меняет подход к конструированию частных методов распознавания, позволяя создавать адаптивные алгоритмы, зависящие от некоторых изменяемых в процессе обработки допусков, и обладающие метриками качества, которые можно вычислить на этапе структурной обработки.
Уровень растра: загрузка изображения
Поскольку мы использовали замечательную библиотеку OpenCV, этот этап максимально прост. OpenCV умеет грузить множество популярных растровых форматов: PNG, JPG, BMP, DIB, TIFF, PBM, RAS, EXR, причем фактически одной строкой:
cv::Mat mat = cv::imread(fname, CV_LOAD_IMAGE_GRAYSCALE);
Выбранный параметр CV_LOAD_IMAGE_GRAYSCALE позволяет загрузить картинку в виде матрицы интенсивностей пикселей (преобразование в градации серого будет происходить автоматически). В ряде задач необходимо использование цветовой информации, но в нашей — это не нужно, что позволяет существенно сэкономить выделение памяти. Из подвохов, разве что загрузка «прозрачных» PNG, — прозрачный фон будет трактоваться как черный, что легко обходится загрузкой с параметром CV_LOAD_IMAGE_UNCHANGED и ручной обработкой цветовой BGRA-информации (да, OpenCV хранит данные цвете именно в таком порядке).
Пусть на данном этапе мы получим что-то вроде такого: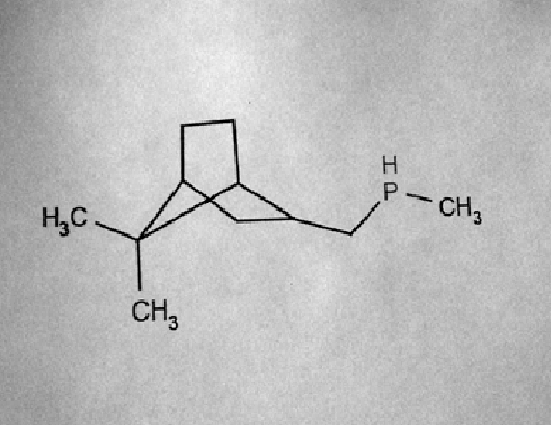 
Я совершенно сознательно выбрал картинку «похуже», чтобы показать, что оптическое распознавание связано с многочисленными сложностями, которые мы будем решать дальше, но она из «реальной жизни» — камеры мобильных телефонов «и не такое могут».
Уровень растра: предварительная фильтрация
Основная задача предварительной фильтрации — улучшить «качество» изображения: убрать шум, без потерь в детализации и восстановить контрастность.
Вооружившись графическим редактором можно прикинуть много хитрых схем, как улучшить качество изображения, но здесь важно понимать границу между тем, что можно сделать автоматически, а что — является вымыслом, применимым ровно к одному изображению. Вот примеры более-менее автоматизированных подходов: разреженные маски, медианные фильтры, для тех, кто любит гуглить.
Хотелось бы провести сравнение методов, и показать, почему мы выбрали определенный, но практически — это сложно. На различных изображениях у определенных методов есть свои преимущества и свои недостатки, «в среднем» лучшего решения тоже нет, посему в Imago OCR мы спроектировали стек фильтров, каждый из которых может применяться в определенных случаях, а выбор результата будет зависеть от метрики качества.
Но хочется рассказать об одном интересном решении: Retinex Poisson Equation
К преимуществам метода можно отнести:
- Довольно высокую скорость работы;
- Параметризуемое качество результата;
- Отсутствие размывания в ходе работы, и как следствие, «чуткость» к деталям;
- И главная интересная особенность — нормализация локальных уровней освещенности.
Последнее свойство отлично иллюстрируется изображением из статьи, а важным для распознавания оно является из-за возможной неоднородности освещения объектов при съемке (листок бумаги, повернутый к источнику света так, что свет падает неравномерно):
Поверхностное описание алгоритма:
- Локальной пороговой фильтрации изображения (laplacian threshold) с порогом T;
- Дискретном косинусном преобразовании полученного изображения;
- Фильтрации высокочастотных характеристик и решении специального уравнения для низких и средних частот (Retinex Equation);
- Обратном дискретном косинусном преобразовании.
Сам алгоритм довольно чутко зависит от параметра T, но мы использовали его адаптацию:
- Считаем Retinex(T) для T=1,2,4,8
- Выполняем попиксельную медианную фильтрацию между результатами Retinex
- Нормализуем контрастность
Чем поможет OpenCV: есть готовая функция вычисления дискретного косинусного преобразования:
void dct(const Mat& src, Mat& dst, int flags=0); // flags = DCT_INVERSE for inverse DCT
И она по скорости работает не хуже, чем аналогичная из libfftw, хоть и не берусь утверждать это в общем случае (тестировалось на Core i5, Core Duo).
Для исходной картинки вышеописанный метод дает довольно приятный результат:
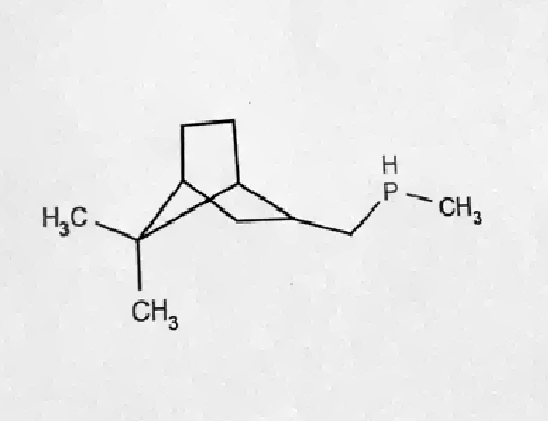
Теперь мы примерно понимаем, что должна делать предварительная фильтрация, и у нас уже появился один параметр, который может меняться в механизме обратной связи: индекс используемого фильтра.
Здесь и далее: по факту, конечно есть множество других параметров (например, те самые, «магические» T=1,2,4,8), но, дабы «не забивать голову», не будем про них говорить сейчас. Их много, упоминания про них всплывут в разделе о машинном обучении, но конкретику я опущу, дабы не перегружать изложение количеством параметров.
Уровень растра: бинаризация
Следующим шагом является получение черно-белого изображения, где черный будет отвечать наличию «краски», а белый — ее отсутствию. Делается это потому, что ряд алгоритмов, например получение контура объекта, конструктивно не работают с полутонами. Одним из самых простых способов бинаризации является пороговая фильтрация (выбираем t в качестве порогового значения, все пиксели с интенсивностью больше t — фон, меньше — «краска»), но в силу ее низкой адаптивности чаще используется otsu threshold или adaptive gaussian threshold.
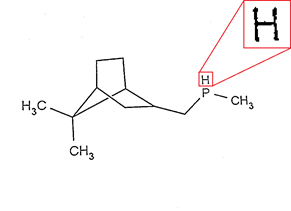
Несмотря на адаптивность более продвинутых методов, они все равно содержат пороговые значения, определяющие «количество» выходной информации. В случае более жестких порогов — часть элементов может быть потеряна, в случае «мягких» — может вылезти «шум».
| Strong thresholding | Weak thresholding |
 |
 |
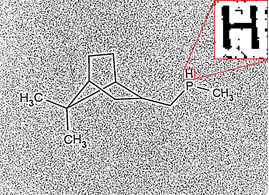Можно пытаться точно угадать пороги для каждого изображения, но мы пошли другим путем — использовали корреляцию между полученными изображениями с различными адаптивными порогами бинаризации:
- Считаем strong и weak бинаризацию (с заданными порогами t1 и t2);
- Разбиваем изображения на набор связных попиксельно областей (маркировка сегментов);
- Удаляем все «слабые» сегменты, имеющие корреляцию с соответствующими сильными, меньше заданной (cratio);
- Удаляем все «слабые» сегменты небольшой плотности (пропорции черных/белых пикселей меньше заданной bwratio);
- Оставшиеся «слабые» сегменты — результат бинаризации.
В результате в большинстве случаев получаем изображение, лишенное шума и без потерь в детализации:
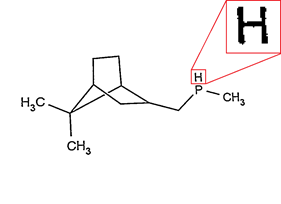
Описанное решение может выглядеть странно, в свете того, что мы хотели «избавиться» от одного параметра, а ввели целую кучу других, но основная идея в том, что корректность бинаризации теперь обеспечивается, в случае, если «настоящий» порог бинаризации попадает в интервал, заключенный между выбранными нами t1 и t2 (хотя мы не можем «бесконечно» увеличивать этот интервал, на разницу t1 и t2 тоже есть ограничение).
Идея вполне жизнеспособна при применении с различными методами пороговой фильтрации, а OpenCV «помогла» наличием встроенных функций адаптивной фильтрации:
cv::adaptiveThreshold(image, strongBinarized, 255, cv::ADAPTIVE_THRESH_GAUSSIAN_C, CV_THRESH_BINARY, strongBinarizeKernelSize, strongBinarizeTreshold);
cv::threshold(image, otsuBinarized, otsuThresholdValue, 255, cv::THRESH_OTSU);
Если итоговое изображение вообще не содержит сегментов, то вероятно, произошла ошибка фильтрации и стоит рассмотреть другой предварительный фильтр («обратная связь»; «те самые» голубые стрелки в изображении структуры движка).
Уровень примитивов: векторизация
Следующим шагом в процессе распознавания является преобразование наборов пикселей (сегментов) в примитивы. Примитивами могут быть фигуры — окружность, набор сегментов, прямоугольник (конкретный набор примитивов зависит от решаемой задачи), или же символы.
Пока мы не знаем к какому классу отнести каждый объект поэтому пытаемся векторизовать его различными способами. Один и тот же набор пикселей может быть успешно векторизован и как набор сегментов и как символ, например «N», «I». Или же окружность и символ — «O». На данном этапе нам не нужно знать достоверно, какой класс имеет объект, но необходимо иметь определенную метрику схожести объекта с его векторизацией в определенном классе. Обычно это решается набором распознающих функций.
Например для набора пикселей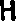 
мы получим набор следующих объектов (не думайте о конкретных числах метрики, они приведены для изображения того, чего мы хотим от процесса распознавания, но сами по себе пока не имеют смысла):
- векторизация в виде символа «H» с значением метрики (расстояния) в 0.1 (возможно это именно H);
- векторизация в виде символа «R» с значением метрики в 4.93 (маловероятно, но возможно это и R);
- векторизация в виде трех сегментов "|", "-", "|" с значением метрики в 0.12 (вполне возможно, что это три сегмента);
- векторизация как прямоугольник с размерами сторон x, y с значением метрики в 45.4 (совсем не похоже на прямоугольник);
- векторизация как окружности с значением метрики +inf (гарантировано не является окружностью);
- ...
Для того чтобы получить список векторизаций необходимо реализовать примитивы распознавания для каждого конкретного класса.
Распознавание набора сегментов
Обычно растровая область векторизуется в набор сегментов следующим образом:
- Выполнение thinning фильтра (
-> 
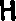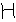); - Разбиение на сегменты (decorner) (
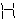); - Аппроксимация точек каждого сегмента;
- Результат — набор аппроксимаций и отклонение аппроксимации от оригинала.
Готового thinning фильтра в OpenCV нет, но реализовать его совсем не трудно. Разбиения на сегменты (decorner) тоже, но это и вовсе тривиально: выкидываем из области все точки, у которых больше двух соседей. А вот аппроксимация точек как набора сегментов в OpenCV присутствует, ей мы и воспользовались:
cv::approxPolyDP(curve, approxCurve, approxEps, closed); // approximation of curve -> approxCurve
Важным параметром является допуск аппроксимации (approxEps), при увеличении которого в качестве результата мы получим большее число сегментов, а при уменьшении — более грубое приближение, и, как следствие, большее значение метрики. Как правильно его выбирать?
Во-первых он достаточно сильно зависит от средней толщины линии (интуитивно — чем больше толщина линии, тем меньше детализация; рисунок нарисованный острым карандашом может быть значительно более детализован, чем нарисованный маркером), что мы и использовали в нашей реализации:
approxEps = averageLineThickness * magicLineVectorizationFactor;
Во-вторых, с учетом вышеописанного подхода к классификации объектов есть возможность пытаться векторизовать сегменты с разными approxEps (с определенным шагом) и уже на этапе анализа логической структуры выбрать «более подходящий».
Распознавание окружностей
Довольно просто:
- Ищем центр окружности (среднее по координатам точек) — (x,y);
- Ищем радиус (среднее расстояние точек от центра) — r;
- Считаем погрешность: среднее расстояние по точкам до окружности с центром (x,y) и радиусом r и толщиной averageLineThickness;
- Считаем дополнительный штраф за разрывы окружности: magicCirclePenalty * (%разрывов).
После подбора magicCirclePenalty с этим кодом совершенно не было проблем, как и с похожим на него распознаванием прямоугольников.
Распознавание символов
Значительно более интересная часть, т.к. это challenge problem — нет ни одного алгоритма, претендующего на «самые оптимальные» показатели распознавания. Есть совсем простые методы, опирающиеся на эвристику, есть более сложные, например с использованием нейронных сетей, но никакие не гарантируют «хорошего» качества распознавания.
Поэтому довольно естественным казалось решение использовать несколько подсистем распознавания символов и выбора агрегатного результата: если p1 = метрическое значение того, что алгоритмом 1 область A распознается как символ s, а p2 = метрическое значение того, что алгоритмом 2 область A распознается как символ s, то итоговое значение p = f(p1,p2). Нами было выбрано два алгоритма, обладающие удобно сравниваемыми значениями, высокой скоростью и достаточной стабильностью:
- распознавание на базе дескрипторов Фурье;
- маски квадратичного отклонения точек.
Распознавание символов на базе дескрипторов Фурье
Подготовка:
- Получение внешнего контура объекта;
- Преобразование координат точек контура (x;y) в комплексные числа x+iy;
- Дискретное преобразование Фурье набора этих чисел;
- Отбрасывание высокочастотной части спектра.
При выполнении обратного преобразования Фурье мы получаем набор точек, описывающий исходную фигуру с заданной степенью аппроксимации (N — количество оставленных коэффициентов):
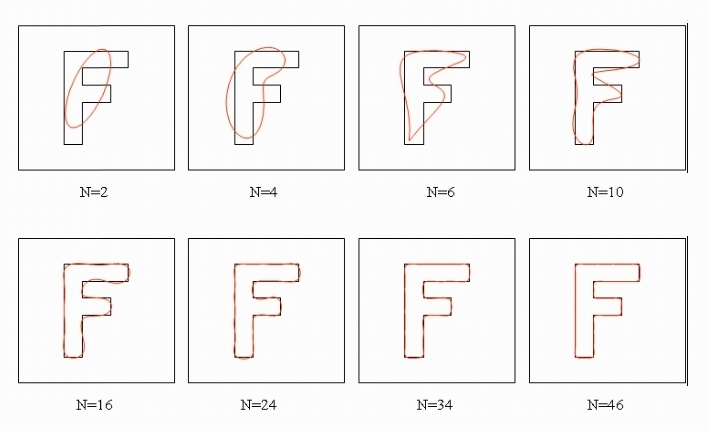
Операция «распознавания» заключается в вычислении дескрипторов Фурье для распознаваемой области и сравнение их с предопределенными наборами, отвечающими за поддерживаемые символы. Чтобы получить метрическое значение из двух наборов дескрипторов необходимо выполнить операцию, называющуюся сверткой: d = sum((d1[i]-d2[i])*w[i], i=1,N), где d1 и d2 — наборы дескрипторов Фурье, а w — вектор весов для каждого коэффициента (мы получали его машинным обучением). Значение свертки инвариантно относительно масштаба сравниваемых символов. Кроме того, функция устойчива к высокочастотному шуму (случайных пикселях, не меняющих «геометрию» фигуры).
OpenCV довольно сильно помогает в реализации этого метода; есть готовая функция получения внешних контуров объектов:
cv::findContours(image, storage, CV_RETR_EXTERNAL);
И есть функция вычисления дискретного преобразования Фурье:
cv::dft(src, dst);
Остается только реализовать свертку и промежуточные преобразования типов, сохранение набора дескрипторов.
Метод хорош для рукописных символов (пожалуй наверное потому, что на него фоне другие дают менее качественные результаты), однако плохо пригоден для символов небольшого разрешения из-за того, что высокочастотный шум, то бишь «лишние» пиксели становятся большими по отношению к изображению целиком и начинают влиять на те коэффициенты, которые мы не отбрасываем. Можно пытаться уменьшить количество сравниваемых коэффициентов, но тогда становится сложнее делать выбор из схожих небольших символов. И поэтому был введен еще один метод распознавания.
Распознавание символов на базе масок квадратичного отклонения
Это довольно-таки интуитивное решение, которое, как оказалось, прекрасно работает для печатных символов любых разрешений; если у нас есть два черно-белых изображения одинакового разрешения, то можно научиться сравнивать их попиксельно.
Для каждой точки изображения 1 считается штраф: минимальное расстояние до точки изображения 2 того же цвета. Соответственно, метрика — это просто сумма штрафов с нормализующим коэффициентом. Такой метод будет значительно более устойчив на изображениях небольшого разрешения с наличием шума — для изображения с длиной стороны n отдельные пиксели в числе до k процентов не «испортят» метрику более чем k * n в худшем случае, а в практических — не более чем на k, ибо в большинстве случаев прилегают к «правильным» пикселям изображения.
Минусом метода, в том изложении как я описал, будет являться низкая скорость работы. Для каждого пикселя (O(n2)) мы считаем минимальное расстояние до пикселя того же цвета другой картинки (O(n2)), что дает O(n4).
Но это довольно легко лечится предвычислением: построим две маски penalty_white(x,y) и penalty_black(x,y) в которых будут храниться предвычисленные значения штрафов за то, что пиксель (x,y) оказывается white или black соответственно. Тогда процесс «распознавания» (то есть вычисления метрики) укладывается в O(n2):
for (int y = 0; y < img.cols; y++)
{
for (int x = 0; x < img.rows; x++)
{
penalty += (image(y,x) == BLACK) ? penalty_black(y,x) : penalty_white(y,x);
}
}
Остается только хранить маски (penalty_white, penalty_black) для каждого написания каждого символа и в процессе распознавания их перебирать. OpenCV в реализации этого алгоритма нам практически не поможет, но он тривиален. Но, как я уже говорил, сравниваемые изображения должны быть одинакового разрешения, поэтому чтобы привести одно к другому возможно потребуется функция:
cv::resize(temp, temp, cv::Size(size_x, size_y), 0.0, 0.0);
Если вернуться к общему процессу распознавания символов, то в результате прогона обоих методов мы получаем таблицу метрических значений:
Значение распознавания — не один элемент, а вся таблица, из которой мы знаем, что с самой большой вероятностью — это символ «C», но возможно это «0», или «6» (или «O», или «c», которые не влезли на экран). А если это скобка, то с большей вероятностью открывающая, нежели закрывающая. Но пока мы даже не знаем, символ ли это вообще…
Уровень примитивов: сепарация
Если бы мы жили в идеальном мире сверхпроизводительных (квантовых?) компьютеров, то скорее всего этот шаг не был бы необходим: у нас есть набор некоторых объектов, для каждого из которых есть таблица «вероятностей», определяющая, что именно это. Перебираем все элементы в таблице для каждого объекта, строим логическую структуру, и выбираем самую вероятную (по сумме метрик отдельных объектов) из валидных. Делов-то, кроме разве что экспоненциальной сложности алгоритма.
Но на практике обычно требуется определить тип объекта по-умолчанию. То есть выбрать некоторую готовую трактовку объектов на изображении, а затем, возможно незначительно ее изменить. Почему мы не могли выбрать тип объектов на предыдущем шаге (векторизации)? У нас не было достаточно статистической информации о всех объектах, и если трактовать определенный набор пикселей изолированно от всей картинки, то достоверно определить его смысл становится проблематично.
Это один из самых важных вопросов распознавания структурной информации. У человека с этим все обстоит значительно лучше, чем у машины, ибо он просто не умеет видеть пиксели по отдельности. И одним из начальных этапов разочарования в построении OCR системы является попытка алгоритмизировать вроде бы человеческий подход «по шагам» и получение при этом неудовлетворительных результатов. Кажется что вот-вот уже, стоит немного улучшить алгоритмы распознавания примитивов, чтобы они «не ошибались», и мы получим более качественные результаты, но всегда находится несколько картинок, которые «ломают» любую логику.
И вот, мы спрашиваем человека, что это — 
Конечно, это просто изогнутая линия. Но если нужно причислить ее либо к символам, либо к набору сегментов прямой линии, то что это? Тогда это, скорее всего, либо буква «l», либо две прямые линии под углом (просто угол нарисован скругленным). Но как выбрать правильную трактовку? Примерную задачу могла решать и машина на предыдущем шаге, и решить ее верно с вероятностью 1/2. Но 1/2 это полный крах для системы распознавания структурной информации, мы просто испортим структуру, она не пройдет валидацию, придется исправить «ошибки», которые по счастливой вероятности могут не совпасть с истинной проблемой. Мы можем получить все что угодно.
Но если мы посмотрим на соседние объекты, то многое может стать понятным:
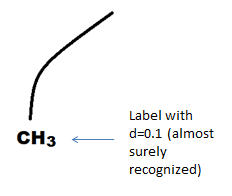
И пусть вы даже не сталкивались с структурными формулами в химии никогда, но из этой картинки почему-то становится очевидно что это связь (линия, прямая или две прямых с скругленным углом). Мы видим изображение трех символов, видим какие они аккуратные, оцениваем примерный их размер, понимаем что «скругленная штука» — не символ.
Есть и другой вариант:
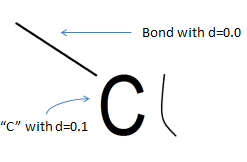
Мы увидели линию, которая является абсолютно прямой, увидели стоящий рядом «идеальный» символ, наш объект похож по размеру, хотя и отрисован менее качественно. Здесь сложнее сказать наверняка, но если мы знаем, что связи должны соединять объекты, а в направлении концов нашего объекта ничего нет — то он вряд ли связь. А если вспомнить, что «Cl» (хлор) вполне вероятное сочетание символов в нашей предметной области, то да, это все-таки символ «l».
Здесь я практически и изложил в свободном стиле наброски алгоритма сепарации. А теперь более формально.
Пороговая часть:
- Если в таблице метрик для объекта только одно значение является «хорошим» (близким к нулю), а все остальные отличаются минимум на константу C, то маркируем его соответствующим классом.
Это здорово, но так бывает не всегда.
Для оставшихся объектов прибегаем к статистическому анализу:
- Определение среднего размера потенциальных символов и отклонения от него;
- Определение средней длины потенциальных линий, отклонение от него;
- Определение средней кривизны потенциальных линий;
- Определение средней толщины линий, символов;
- И другие статистические критерии, например hu moments (которые кстати OpenCV умеет считать).
Мы все еще не знаем, для каждого объекта — какой класс он имеет, просто смотрим в таблицу метрик, и выбираем наиболее близкий по значению к нему объект — это я и вкладываю в понятие "потенциальный".
Затем строим дерево классификации, в узлах которого могут стоять следующие условия: (если высота объекта лежит в диапазоне от средняя_высота_символа-1 до средняя_высота_символа+2, при этом обладает кривизной превосходящей 3*средняя_кривизна_линии и его длина менее 0.5*средняя длина линий), то он маркируется как символ. Метод построения деревьев классификации хорошо описан здесь, и я позволю себе не повторять.
После прохождения статистической части некоторые объекты будут промаркированы предположительными классами. В большинстве практических случаев — почти все объекты. Если нам не удалось промаркировать хотя бы половину объектов, то скорее всего, что-то у нас пошло не так (и такое часто бывает для рукописных картинок). Но не будем «отчаиваться» и просто выберем половину объектов с наименьшими метрическими значениями и промаркируем их без учета статистической информации (для этой странной загогулины из примера — просто посмотрим в таблицу расстояний, и если к «l» она ближе, то назначим ее символом «l». Какие при этом могут возникать проблемы я уже описал, но это вынужденное решение).
Для оставшихся объектов применим локальный анализ:
- Найдем всех соседей для выбранного объекта;
- Если часть соседей уже имеет выбранный класс, то выберем из таблицы вероятности локальных конфигураций более вероятную;
- Дополнительно: если в направлении концов объекта не стоит стоит других объектов, то он символ.
Для оставшихся объектов класс выберем «по умолчанию» — тот что по метрическому значению ближе.
В результате всех мучений мы можем разделить изображение к набор объектов, предположительно являющихся символами и часть, отвечающую за структуру.
Структурный уровень
Теперь осталось собрать из набора элементов готовую структуру. Здесь, конечно сами алгоритмы начинают сильно зависеть от предметной области.
Не вдаваясь в химические детали, в Imago OCR мы работаем с изображениями молекул, которые по сути представляют граф связей, в вершинах которого стоят метки (набор символов), поэтому сама задача сборки структуры довольно тривиальна. Но не любая комбинация символов является валидной меткой атома, и не из любого набора отрезков можно построить корректный граф. Метки могут использовать нижние и верхние индексы, знаки зарядов и скобочные последовательности. Для дальнейшего изложения я выберу самые интересные, и возможно потенциально полезные моменты.
Обработка графа структуры
Первым важным шагом, является собственно получение этого графа. После векторизации, все что мы имеем — набор разрозненных сегментов, у каждого из которых есть «начало» и «конец», которые я на изображении структуры промаркировал окружностями:
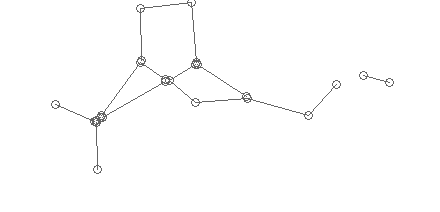
Статистически мы определяем средний радиус возможной склейки, и «собираем» отрезки, концы которых лежат в этом радиусе в вершины графа:
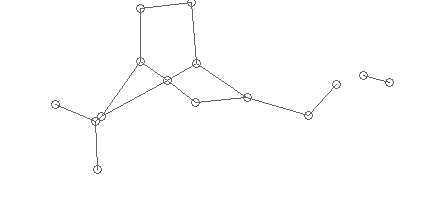
Радиус можно определить так — для каждой вершины посчитать минимальное расстояние до соседей и найти пик гистограммы. В случае, если этот пик дает радиус, больший среднего размера символа, то можно считать, что все отрезки не связаны.
Затем удаляем слишком короткие ребра:
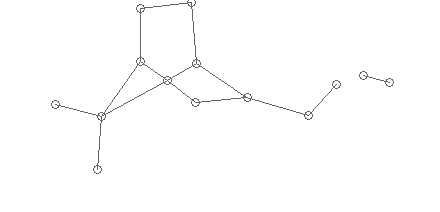
Слишком короткие ребра — результат векторизации линий с артефактами (изгибы, пиксельный шум). У нас есть средний размер символа, можно считать, что длина связей, меньшая размера символа — невозможна (за рядом исключений, которые проверяются специальным образом — химическая специфика).
Вышеописанные пункты будут полезны и при распознавании таблиц, к примеру. А у нас есть еще поиск кратных ребер, нахождение «мостов» (планарного изображения непересекающихся ребер), нахождение изображения «стрелок». Все это значительно удобнее делать, работая с структурой графа, а не с промежуточными результатами распознавания — не стоит добиваться «идеальной» векторизации.
Сборка и обработка меток
Для символов необходимо выполнить объединение в группы и здесь применяется решение, аналогичное «сборке» графа. Каждую собранную метку необходимо распознать, а поскольку могут присутствовать верхние и нижние индексы — задача становится интереснее.
Для начала вычисляется «базовая линия» метки: 
Это прямая (по сути просто определенное значение baseline_y), над которой лежат заглавные символы метки, а под которой — индексы. Для определения baseline_y нам поможет статистика:
- определение среднего размера заглавного символа (у большинства символов написание заглавных и прописных различаются);
- при анализе каждой конкретной метки выбираем среднее значение координаты y для всех символов, размер которых находится в пределах среднего.
Почему мы берем среднее, а не максимум (линия же должна идти под символами метки)? Так стабильнее; если мы ошиблись с трактовкой символа как заглавного, мы можем ошибочно причислить индекс к заглавным, провести под ним черту, и соответственно «индексов у нас больше не будет». Выбор среднего же с одной стороны не значительно меняет значение baseline_y в хороших случаях, а с другой — цена ошибки неправильного выбора заглавных символов падает.
Затем распознаем символы, один за другим. Для каждого символа вычисляем:
- % его высоты, лежащей под базовой линией;
- отношение к средней высоте заглавных символов.
Довольно неудачным было бы пороговое решение относительно этих параметров: если под базовой линией находится минимум 30% символа — то он индекс. А если 29? Вообще весь процесс распознавания как нельзя лучше можно описать идеей duck test. Если что-то похоже на индекс, то скорее всего — оно индекс. А похоже оно на индекс, если на что-то другое оно похоже еще меньше.
Что увеличивает вероятность символа быть индексом? Чем меньше он, и чем ниже относительно базовой линии. А еще у цифр вероятность быть индексом больше. Одной из хороших идей при распознавании было использование набора изменений списка метрик (вы еще помните, что для каждого объекта мы храним все возможные похожие на него объекты?). Теперь в этот набор метрик добавляются еще и трактовки как нижние индексы. Это значения метрики, изначально скопированные из обычных значений в процессе распознавания изменяются:
- Если символ лежит на k% ниже базовой линии, то метрика для его трактовок как нижнего индекса уменьшается в f(k) раз;
- Если символ на n% меньше по высоте, чем средняя высота, то метрика для его трактовок как символ a..z уменьшается в g(n) раз.
Соответственно в процессе распознавания, после применения всех правил мы просто выбираем трактовку с наименьшим значением метрики — это победивший символ, самый похожий. Но мы все еще не будем «забывать» остальные трактовки.
Валидация меток
Следующим шагом после получения готовых трактовок меток целиком — является их валидация. В каждой предметной области — она своя: для русского языка — это проверка по словарям, для ряда идентификаторов это могут быть контрольные суммы, а в химии — набор допустимых элементов. Для реализации именно этой части мы все еще держим полный набор альтернатив для каждого объекта.
Пусть наша метка состоит из двух символов: {c1, c2}
Причем c1 — это «Y» с значением метрики 0.1 и «X» с значением метрики 0.4;
c2 — это «c» с значением метрики 0.3 и «e» с значением метрики 0.8
Я бы просто мог написать, что наша метка — Yc. Но метка Yc не валидна. Чтобы получить валидную метку мы можем перебрать возможные альтернативы и выбрать валидную. Среди валидных ту — у которое суммарное значение метрик минимально.
В данном случае из всех 4 вариантов, валиден только один "Xe", дающий итоговую метрику 1.2.
Вроде бы мы решили проблему, теперь значение метки валидное. Но как быть, если именно «Yc» и хотел использовать автор картинки, вопреки корректности. Для того чтобы это понять, мы вычитаем новое значение метрики (1.2) из старого (0.4), и трактуем полученную разницу (0.8). Ее можно сравнить с определенным порогом, и запретить коррекцию, если она его превосходит. Но как выбрать этот порог?
Машинное обучение
Как вообще выбирать многочисленные константы, пороговые ограничения, используемые в процессе распознавания? Начальные значения, конечно можно выбрать исходя из здравого смысла, но будут ли они оптимальными?
Решение подобных проблем можно частично поручить машине — выполнять случайные изменения параметров и выбирать те, которые дают в среднем лучший результат. Случайные изменения можно систематизировать, используя модификацию генетического алгоритма, что мы и сделали.
Но следует понимать, что процесс распознавания с вычислительной точки зрения — черный ящик, и на некоторых наборах параметров он может работать неопределенно долго. Для этого мы использовали замеры времени выполнения и ограничение тех наборов, на которых это время значительно увеличивалось. Этот подход показал свою эффективность в большинстве случаев.
Тематика заслуживает отдельной заметки, но сейчас в качестве тезиса, скажу, что обучение системы, собранной из адаптивных функциональных блоков работает значительно эффективнее, чем обучение нейронной сети, основанной на пороговых функциях активации; констант меньше и у каждой есть непосредственное (и обычно объяснимое) влияние на результат. Их можно было бы выбрать и вручную, но взаимосвязь параметров, и правильное их изменение после частичного изменения алгоритмов — сложная для человека задача.
Вместо заключения
Многое осталось «в тени» и до создания руководства построения системы OCR еще далеко, если вообще ставить подобную цель. Хотелось бы, что бы из заметки было понятно, какие проблемы могут возникнуть, какие возможные пути их решения существуют, и что между алгоритмом распознавания символов и построением полноценной системы оптического распознавания структурной информации есть существенная разница. Я буду рад конструктивной критике и предложениям по дополнению заметки.
Кроме того, если будет интересна реализация изложенных в заметке методов, продублирую ссылку на open-source проект Imago OCR, обсуждение и предложения по развитию которого приветствуются в соответствующей группе google.
Автор: sic
