В ставших уже традиционными ежемесячных конкурсах по функциональному программированию всем желающим предлагается поразмять свои и представить на суд общественности своё решение конкурсной задачи на каком-либо языке программирования (кстати, совсем не обязательно функциональном — многие конкурсанты используют и такие экзотические языки, как Java и даже Python). В апрельском конкурсе в качестве задачи была предложена задача по поиску цепочки трансмутаций между словами в заданном словаре. Конечно, это есть задача по поиску [кратчайшего] пути в графе, рёбра которого представляют возможность перехода от слова к слову по заданному правилу (должна быть изменена и только изменена одна и только одна буква), однако задача заинтересовала участников, и в качестве результатов было представлено 22 решения на 9 различных языках (C++, Clojure, D2, Erlang, F#, Go, Haskell, Mathematica и Perl).
Словарь, по которому осуществлялся поиск, можно получить здесь. Впрочем, можно воспользоваться услугами сайта «Слова из букв», с которого, собственно, и получен словарь. Конечно, многие слова там очень странные, однако какая нам разница, на каком словаре строить граф для конкурса? Пусть это будут просто формальные цепочки символом. А по результатам конкурса вообще появлялись такие предложения от участников: «Надо написать новое определение слова «АХЧЕ» — это слово, которое используется в конкурсах по программированию, для порождения самых длинных метаграмм».
Ну а поскольку конкурс был назван «Кельтская алхимия», занимались мы трансмутациями следующих пар слов (метаграмм):
- МУХА — СЛОН
- ДЕНЬ — НОЧЬ
- СНЕГ — ВОДА
- ОТЕЦ — МАТЬ
- РУКА — НОГА
- ЗИМА — ЛЕТО
- СВЕТ — ТЬМА
- ЛИПА — КЛЁН
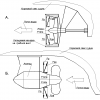
Как видно, здесь имеет место попытка подобрать слова, часто противоположные по смыслу. Это придало конкурсу некоторую изюминку, хотя, конечно, все участники подошли к этому вопросу абсолютно по программистски — все разработали алгоритмы поиска путей в графе. А кое-кто даже граф визуализировал:
Итак, если вам интересна задача, и вы хотите узнать, как организовывался конкурс и как можно решить поставленную задачу, то милости прошу дальше…
Составление словаря
Первым делом я озаботился составлением единого словаря для конкурса, ведь все участники должны решать одну и ту же задачу, если мы хотим сравнивать их решения. Беглый поиск по этим вашим интернетам показал, что более или менее годный словарь содержится только на указанном выше сайте. Его надо было обработать, предварительно выкачав. Выкачку я осуществил вручную, а вот для обработки была написана маленькая утилита. Разберём её подробнее.
Для работы нам потребуется описание такой структуры данных, как ByteString, причём в двух инкарнациях — обычной ленивой и восьмибитовой. Вот и импортируем необходимые модули:
module Vocabulary where
import Data.ByteString (ByteString)
import qualified Data.ByteString as BS
import qualified Data.ByteString.Char8 as BS8 (pack, takeWhile)
import System.IO
Исповедуя принцип разработки сверху-вниз, с самого начала напишем функцию main:
main :: Int -> Int -> IO ()
main l n = do hs <- mapM (`openFile` ReadMode) $ createFileNames l [1..n]
mapM_ (`hSetEncoding` utf8) hs
cnts <- mapM BS.hGetContents hs
saveVocabulary l $ getWords $ BS.concat cnts
mapM_ hClose hs
Что же тут? А тут показан один из мощнейших приёмов монадических вычислений, к тому же удостоверяющий, что это именно вычисления в функциональном стиле, а не простая подделка под императивный стиль, как обычно говорят про монаду IO в учебниках и справочниках для начинающих. К тому же, эта монада ленива в языке Haskell, так что ничто не мешает нам выполнить такие интересные конструкции, а именно: создав список имён файлов при помощи функции createFileNames (на её определение мы посмотрим позже), мы открываем файлы всем списком, устанавливаем для всех скопом требуемую кодировку, читаем их содержимое, «склеиваем» содержимое всех файлов вместе, после чего выделяем слова, записываем их и опять же скопом закрываем все файлы-исходники. Красота!
Итак, функция main получает на вход два параметра. Первый — это количество букв в выделяемых словах. Второй — количество файлов, из которых надо выделить слова. Оба этих параметра используются для создания списка имён файлов-исходников. Вот её определение:
createFileNames :: Int -> [Int] -> [FilePath]
createFileNames l = map (n -> show l ++ "-" ++ (if n < 10
then ('0' :)
else id) (show n) ++ ".htm")
Здесь всё просто. Функция создаёт список строк вида «l-nn.htm». Да, это очень частно, поскольку получается, что таких файлов может быть не более 99 (от 1 до 99). Но для быстрого сбора данных пойдёт. Впрочем, сделать функцию более универсальной было бы хорошо. Оставляется это на усмотрение вдумчивым читателям.
Следующая функция, которую надо реализовать, сохраняет список выделенных слов в файле. Первым параметром ей задаётся размер слов (в буквах), и это число используется в названии сохраняемого файла. Вот её определение:
saveVocabulary :: Int -> [ByteString] -> IO ()
saveVocabulary l ws = do h <- openFile ("Vocabulary-" ++ show l ++ ".txt") WriteMode
hSetEncoding h utf8
mapM_ (BS.hPutStrLn h) ws
hClose h
Опять же, в данном определении ничего сложного нет. Открывается файл на запись, при этом имя файла представляет собой строку вида «Vocabulary-l.txt», где l — размер слов в буквах. Не забываем про кодировку, ибо работаем мы, в общем-то, с русским языком. Опять же скопом при помощи прекрасной функции mapM сохраняем все найденные строки в файле, после чего закрываем его. Нигде здесь нет обработки ошибок и исключений, которые могут возникнуть в процессе ввода-вывода, так что эта проблема опять ложится на плечи вдумчивого чистателя :).
Осталось реализовать функцию, выделяющую слова из файлов-исходников. При её определении и становится ясно, для чего нам понадобились строки типа ByteString, а не обычные String, которые вполне бы справились со всем, что описано ранее. Посмотрим на определение, чтобы стало понятно:
getWords :: ByteString -> [ByteString]
getWords cnt = map (i -> BS8.takeWhile (/= '.') $ BS.drop (i + BS.length semaphore) cnt) $
BS.findSubstrings semaphore cnt
Видите? Функция BS.findSubstrings реализована для строк типа ByteString, для обычных строк такой прекрасной функции нет. Не, конечно можно написать самостоятельно (язык Haskell тем и хорош, что если что-то надо написать, то зачастую быстрее написать это самостоятельно, чем лазать по архиву Hackage в поисках готовой реализации; стоимость велосипедиков очень мала). Но в данном случае стоимость велосипеда внушительна (и, кстати, далее это будет ещё раз видно), так что используем готовый модуль с реализацией.
Что у нас здесь? Всё опять же просто. Из огромной строки, созданной при помощи конкатенации содержимого всех файлов-исходников, выделяются индексы начал всех подстрок, задаваемых константной функцией semaphore. Далее при помощи пары функций BS.drop и BS.takeWhile выделяются сами слов. Их список и составляет результат выполнения этой функции. Ну а константа semaphore определяется тривиально (после «ручного» изучения файлов-исходников):
semaphore :: ByteString
semaphore = BS8.pack "<br /><a href="/"
Остаётся привести диаграмму вызова функций. Памятуя о прошлой статье, в комментариях к которой меня отругали за то, что я непочтительно отнёсся к страдающим дальтонизмом, исправляю свою оплошность и вместе с более дружественной раскраской привожу легенду:
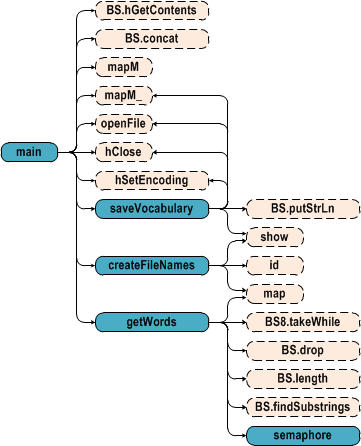
Надеюсь, что теперь всё хорошо.
Решение задачи
Поскольку я часто делаю одновременно тысячу дел, иногда меня на что-то начинает не хватать. Поэтому на этот раз ко мне поспешил на помощь мой добрейший друг lomeo, который не стал мудрствовать лукаво и для реализации решателя поставленной задачи использовал алгоритм A*, пакет для которого уже давно есть в архиве Haskage. Здесь остаётся только кратко рассмотреть реализованные функции на языке Haskell. Опять же, используем разработку сверху-вниз и начинаем с функции main. Но для начала импорт и один синоним типа:
module Alchemy where
import Control.Monad.State
import Data.Char (toUpper)
import Data.Graph.AStar
import Data.Function (on)
import Data.List (intercalate, sortBy, tails)
import Data.Maybe (catMaybes, fromMaybe)
import Data.Ord (comparing)
import System.IO
import qualified Data.Map as M
import qualified Data.Set as S
type SolvingState a = State (M.Map String (S.Set String)) a
Этот синоним используется для сокращения записи монадического типа в монаде State. В качестве состояния используются словарные значения (Map), ключами в которых являются маски (слово с заменённой одной из букв на маску подстановки (_)), а значениями — множества строк, которые могут получиться из этой маски путём подстановки вместо символа (_) какой-либо буквы. Всё это станет понятно из дальнейших определений.
Ну а вот, собственно, определение функции main:
main :: String -> String -> IO ()
main src dst =
if ((/=) `on` length) src dst
then putStrLn "Заданы слова разной длины. Решение задачи невозможно.n"
else catch (do ws <- loadData $ length src
let ps = evalState (createGraph ws >> (solve `on` uppercase) src dst) M.empty
case ps of
Nothing -> putStrLn "Решений не найдено.n"
Just p -> do putStrLn "Решение найдено:"
mapM_ putStrLn p
putStrLn "")
(_ -> putStrLn "Файл со словарём не найден.n")
Тут больше обвязки для обработки всяких нетипичных ситуаций, чем необходимого для решения задачи кода. Самое же главное выражение по существу здесь такое: evalState (createGraph ws >> (solve `on` uppercase) src dst) M.empty. Итак, здесь у нас используются вычисления с состоянием (монада State), причём в качестве состояния выступает граф, составленный из слов (как он создаётся будет показано далее). Функция evalState запускает вычисления с состоянием, передавая в качестве начального состояния пустой граф (M.empty). А граф создаётся при помощи функции createGraph, которой, в свою очередь, передаётся словарь. Ну а словарь надо загрузить. Это делается при помощи функии loadData:
loadData :: Int -> IO [String]
loadData l = do h <- openFile ("Vocabulary-" ++ show l ++ ".txt") ReadMode
hSetEncoding h utf8
cnt <- hGetContents h
return $ lines $ uppercase cnt
Функция ничем не примечательна. Разве что только надо отметить то, что все слова из словаря переводятся в верхний регистр. Это делается для исключения различий между строчными и заглавными буквами при создании графа и поиска решения.
Теперь пришло время для определения самых главных функций — функции создания графа и функции поиска решения. Вот последовательно их определения:
createGraph :: [String] -> SolvingState ()
createGraph = mapM_ addWord
where
addWord word = mapM_ (modify . M.alter (Just . upsert word)) (masks word)
upsert word Nothing = S.singleton word
upsert word (Just wordSet) = S.insert word wordSet
Ой-ёй-ёй, вот в таких определениях, конечно, запутаться можно легко. Но, собственно, ничего страшного тут нет. Надо только помнить, что работа ведётся в рамках монады State. Именно к ней относятся вызовы функции mapM_. Так что пойдём с самого начала. Функция принимает на вход список слов (то есть словарь, на котором надо построить граф). Применяет к каждому слову локально определённую функцию addWord и собирает результаты в состоянии вычислений. Сама же функция addWord обновляет состояние вычислений при помощи обновлённого же графа. Граф обновляется так. По текущему слову строится список масок (вызов функции mask, которая будет описана далее), для каждой маски в этом списке в состояние вносится текущее слово с указанием, что из него можно получить такую-то маску. Каждая маска становится ключом в словаре, а слово заносится в множество, соответствующее этому ключу. Потому и выбран тип Data.Set.Set, он хранит все свои элементы в единственном числе.
Собственно, локальная функция upsert вставляет новое слово во множество. Если множество пустое, то оно создаётся на основе этого слова (вызов S.singleton). Если же множество существует, то слово туда просто добавляется, а сам тип проследит, чтобы слово содержалось в нём в единственном экземпляре.
Чтобы понять, как работает эта функция, надо рассмотреть определени функции masks. Оно несложное:
masks :: String -> [String]
masks [] = []
masks (c:cs) = ('_':cs) : map (c:) (masks cs)
Всё, что она делает, так это конструирует список из заданной строки, подставляя вместо каждой буквы символ подстановки (_). Так что из слова «МУХА» данная функция сделает список ["_УХА", "М_ХА", "МУ_А", "МУХ_"]. Рекомендуется внимательно изучить определение этой функции, чтобы понять, как она работает. Её определение очень хорошо отражает суть функционального программирования на языке Haskell.
Итак, применив функцию addWord к слову «МУХА», в состояние вычислений попадёт словарь, содержащий четыре элемента. Ключами будут перечисленные четыре элемента списка, возвращённого функцией masks, а значениями будут синглетоны (множества с одним элементом) со словом «МУХА». Что же теперь произойдёт, если применить функцию addWord к слову «МАХА»? Функция masks опять вернёт список ["_АХА", "М_ХА", "МА_А", "МАХ_"], при помощи которого обновится состояние вычислений. В словарь попадёт три новых элемента (каких?), а один будет обновлён — это будет элемент, ключём которого является маска «М_ХА». Для него значением станет множество из двух слов — «МУХА» и «МАХА». И вот этот процесс будет повторён для каждого слова в словаре. Теперь понятно, как будет составлен граф.
Теперь перейдём к изучению определения основной функции для поиска решения. Она простая, поскольку вызывает метод из пакета, в котором реализован алгоритм А*:
solve :: String -> String -> SolvingState (Maybe [String])
solve src dst = aStarM adjacent distance heuristic goal start
where
distance w1 w2 = return $ length $ filter not $ zipWith (==) w1 w2
heuristic w = return 0
goal w = return $ w == dst
start = return src
Тут особое внимание стоит уделить локальной функции distance. Она вычисляет расстояние между вершинами в графе. Собственно, кое-кто из конкурсантов пытался в данном случае прицепить расчёт расстояния Левенштейна-Дамерау, однако это не только категорически замедляет алгоритм, но и решает поставленную задачу абсолютно неправильно. Правильная реализация показана здесь — мы просто считаем количество несовпадающих букв. Опять же, рекомендую обратить внимание на это определение (особенно тем, кто только-только начинает изучать язык Haskell и функциональную парадигму программирования) — оно написано прелестно, за исключением того, что можно было бы использовать и бесточеную нотацию (как?).
Ну и напоследок определение функции adjacent, которая определяет сам граф. Помните, граф у нас находится в состоянии вычислений? Так вот эта функция должна для заданной вершины возвращать все смежные с ней. Вот её определение:
adjacent :: String -> SolvingState (S.Set String)
adjacent word = do found <- mapM (gets . M.lookup) (masks word)
return $ S.delete word $ S.unions $ catMaybes found
Опять же, ничего сложного. Берём слово, создаём по нему список масок. Для каждой маски находим все слова, из которых данная маска может быть получена. Полученные множества объединяются, из результата удаляется само слово. И полученное множество и представляет собой смежные вершины.
И последняя функция, определение которой приводится здесь только лишь для полноты:
uppercase :: String -> String
uppercase = map toUpper
Наконец, диаграмма вызовов:
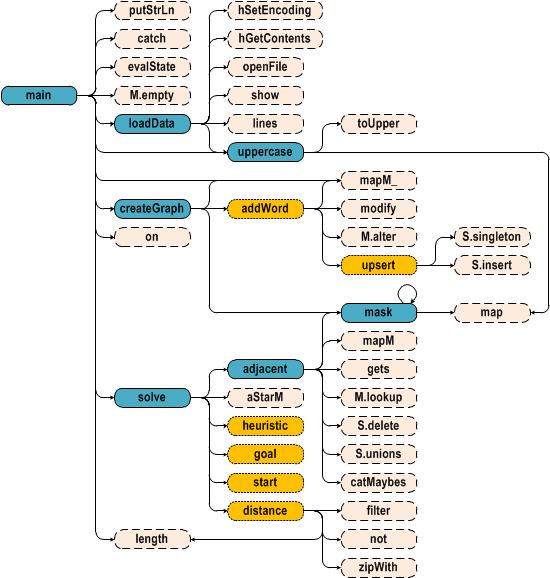
По ней видно, что сложность программы, написанной в данном модуле, намного выше, чем сложность программы из предыдущего модуля (того, который для сбора словарей). Но метрик нет, как я уже говорил, так что пока ограничиваемся визуальным сравнением.
Проверка общности
Как обычно после публикации основных программ я устроил так называемую «проверку общности» реализованных алгоритмов. Чаще всего я даю для решения обратную задачу, что вызывает у некоторых участников конкурсов нестерпимую попоболь. Тем не менее, большинство конкурсантов с обратной задачей справились.
А на этот раз надо было ответить на простой вопрос: необходимо указать длину самой длинной цепочки трансмутации, которая есть в этом словаре. Ну и саму эту цепочку тоже можно указать. Другими словами, надо было найти диаметр графа. Для нахождения ответа на этот вопрос я сам воспользовался функцией:
testGenerality :: IO ()
testGenerality
= do ws <- loadData 4
let ws' = init $ init $ tails ws
graph = execState (createGraph ws) M.empty
pairs = [(fromMaybe [] $ evalState (solve h w) graph, (h, w)) | (h:t) <- ws', w <- t]
(c', (h', w')) = last $ sortBy (comparing fst) pairs
putStrLn ("Самая длинная цепочка трансмутаций длиной " ++ show (length c') ++
" шагов ведёт от слова "" ++ h' ++ "" к слову "" ++ w' ++ "".n")
putStrLn $ intercalate " -> " (h':c')
Эта функция оказалась столь медленной, что мне пришлось ждать примерно полторы тысячи лет, прежде чем я получил результат. Но ничего, дождался…
Ну и тривиальная диаграмма вызовов:
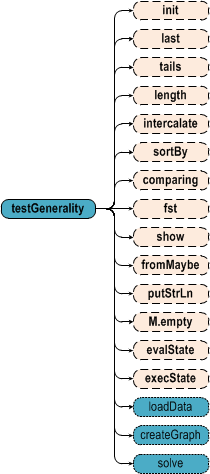
Заключение и некоторые выводы
Предваряя один интересный вопрос, сразу отвечаю, что диаграммы я рисовал при помощи MS Visio вручную. Я их рисую для того, чтобы как-то оценить сложность разработанных модулей. Пока никаких метрик нет, но я думаю над этой проблемой.
Как обычно, модули, описанные в настоящей заметке, вы можете скачать с сервиса hpaste.org (кстати, вы же знали, что он написан на языке Haskell?):
Ну и результаты работы функции поиска решения таковы:
- МУХА — СЛОН: муха маха каха кана канн каин клин клон слон
- ДЕНЬ — НОЧЬ: день мень мель моль мочь ночь
- СНЕГ — ВОДА: нет цепочки трансмутаций
- ОТЕЦ — МАТЬ: отец отек стек стук стул саул сауи сари мари марь мать
- РУКА — НОГА: рука руга нуга нога
- ЗИМА — ЛЕТО: зима зама лама лата лета лето
- СВЕТ — ТЬМА: свет сват сван хван хуан хурн турн тура тора тома тьма
- ЛИПА — КЛЁН: липа кипа кина кана канн каин клин клён
Ответ на дополнительный вопрос о самой длинной цепочке трансмутаций неоднозначен — в словаре есть несколько цепочек длиной 27 слов. Вот одна из них: яшма яшта яхта ухта уста мста мета мера гера гира гирс гиас грас грис арис арии арди эрди энди эндо андо анды анты акты акте акче ахче.
В качестве недоделок и улучшений, которые хорошо бы применить к описанным модулям, надо отметить следующие:
- Реализовать возможность автоматической выкачки всего массива файлов-исходников с сайта для заданной длины слова в буквах.
- Реализовать функцию
createFileNamesболее универсальной, чтобы она могла генерировать «красивые» имена файлов вне зависимости от их количества. - Вплести в код, работающий с вводом-выводом при составлении словарей, обработку ошибок и исключительных ситуаций.
- Для обработки исключений в модуле поиска трансмутаций использовать более мощную функцию
catchиз стандартного модуляControl.Exception. - Необходимо реализовать общую для обоих модулей функцию, возвращающую имя файла со словарём для заданной длины слова в буквах.
Также хотелось бы сообщить, что другой мой добрейший товарищ и коллега afiskon самостоятельно реализовал алгоритм A*, что описал в своей прекрасной заметке «Реализация алгоритма поиска A* на Haskell». Рекомендую.
У Фонда Поддержки Функционального Программирования ФП(ФП) теперь есть свой официальный форум, на котором невозбранно зарегистрироваться и пообщаться с единомышленниками можно здесь.
Если же вы хотите дополнительно отблагодарить автора, но не знаете как, то вам сюда.
Мои предыдущие статьи о конкурсах по ФП на Хаброхабре:
- Решение задачи о перегорающих лампочках на языке Haskell
- Фреймворк для решения задач о переправах на языке Haskell
- Конструирование и вычисление арифметических выражений на языке Haskell
- Расшифровка кода на языке Haskell (конкурс по ФП в январе 2012)
- Шахматные задачи на мат в один ход: решение на языке Haskell
- Измерение объёмов при помощи двух заданных сосудов: решение на языке Haskell
Автор: Darkus
