Как обычно, по чётным месяцам 2013 года проводятся конкурсы по функциональному программированию. Октябрь не стал исключением, и непосредственно на первой неделе был объявлен октябрьский конкурс, который на этот раз был подготовлен великолепным Дмитрием Поповым. Конкурс касался космонавтики — для интересной игры Kerbal Space Program надо было подготовить программное средство для расчёта космических аппаратов. Так что на этот раз конкурс являл собой не только интересное, но и крайне полезное как для ума, так и для прикладного космического искусства дело.
Автор конкурса добавил несколько ограничений — разработанная программа должна находить решение по введённым исходным данным не более, чем за две минуты. Победитель выявлялся на этот раз не просто по скорости публикации решения, но по сумме результатов, которые выдавала программа. Минимальная сумма выявила победителя. И он, кстати, получил, как обычно, памятный приз.
В конкурсе приняли участие четыре конкурсанта, которые успешно написали свои «специализированные калькуляторы». В качестве языков программирования использовались — Clojure, Java, Haskell и Python (перечислены в порядке расположения по занятым местам). В общем, с итогами конкурса всякий может ознакомиться здесь. А мы, пожалуй, перейдём к описанию авторского решения, которое, как обычно, выполнено на языке программирования Haskell.
Немного теории
Итак, кроссплатформенная игра Kerbal Space Program — это симулятор космической программы, где нужно конструировать космические корабли и бороздить ими просторы Вселенной, летая к другим планетам, строя космические станции и т. д. Для строительства кораблей доступно множество готовых частей (двигатели, топливные баки, кабины для космонавтов, вспомогательные маневровые двигатели, парашюты для посадки, крылья и закрылки, лестницы, солнечные батареи и всякое прочее), которые можно комбинировать множеством способов. Задача конкурса — написать программу, которая получит на вход два ключевых параметра (масса полезного груза и бюджет ∆v) и придумает ракету наименьшей массы, способную поднять этот груз в космос и доставить его до цели, обеспечив требуемый бюджет скорости.
Для космического корабля с выключенными двигателями, находящегося в гравитационном поле планеты или звезды, его дальнейшая судьба определяется только его скоростью и не зависит от массы и формы корабля. Если скорость не слишком велика, то в каждый момент времени он движется по орбите вокруг захватившего его небесного тела. Чтобы переместиться от одной планеты к другой, необходимо как минимум дважды поменять текущую орбиту — сперва перейти на эллиптическую орбиту, проходящую мимо обеих планет, затем перейти на орбиту вокруг новой планеты. Каждая такая смена орбиты есть изменение текущей скорости — к старому вектору скорости прибавляется некоторый корректирующий вектор ∆v, и получается новый вектор скорости, соответствующий новой орбите. В промежутках между сменами орбит корабль летит по инерции и топливо не тратит. Стоит заметить, что эта ∆v не зависит от характеристик корабля и зависит только от маршрута: в каком месте с какой орбиты на какую переходит корабль. При планировании межпланетной миссии составляется план маневров, и ∆v всех маневров суммируется в общий бюджет ∆v, который определяет, сколько нужно топлива — если его будет меньше, то пролететь по маршруту не получится, а если слишком много, то корабль выйдет излишне тяжёлым и дорогим.
Для расчёта изменения скорости при использовании ракетного двигателя используется уравнение Циолковского:
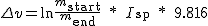
где:
- mstart — общая масса корабля в начале манёвра (в момент включения двигателя);
- mend — общая масса корабля в конце манёвра (в момент выключения двигателя);
- Isp — удельный импульс, характеристика эффективности двигателя;
- 9.816 — используемая в игре константа для g.
Разница между mstart и mend — это масса потраченного во время манёвра топлива. В mstart и mend входит и масса полезного груза, и масса двигателей, соответственно, чем легче корабль, тем больше будет ∆v при тех же затратах топлива и том же двигателе, или, другими словами, тем меньше нужно топлива для достижения заданного ∆v. Когда ракета состоит из нескольких ступеней, отстрел отработавшей ступени резко уменьшает общую массу корабля и тем самым повышает эффективность двигателей очередной ступени. Разные двигатели имеют разную массу и разный удельный импульс. Ещё один важный параметр двигателей — сила тяги, выражаемая в Ньютонах. Некоторые двигатели имеют небольшую массу и большой удельный импульс, что делает их чрезвычайно эффективными по топливу, но при этом они могут иметь совсем небольшую тягу. И если далеко в космосе это может быть приемлемо, то при взлёте с планеты этой тяги может быть недостаточно, чтобы оторваться от поверхности. Кроме того, удельный импульс двигателя может быть различным в вакууме и в атмосфере. Для простоты далее будем считать, что самая первая ступень ракеты (которая включается при старте) работает в атмосфере, а остальные ступени будем рассчитывать с удельным импульсом в вакууме.
Игра позволяет строить весьма разнообразные и причудливые корабли, но для упрощения расчётов и сужения пространства поиска далее вводится ряд ограничений на их структуру. Ракета состоит из нескольких ступеней — при старте начинают работать двигатели первой, самой нижней, ступени, используя топливо из баков первой ступени. Когда топливо в них заканчивается, первая ступень (пустые баки и двигатели) отстреливаются специальным разделителем, после чего тут же начинают работу двигатели второй ступени. И так далее, пока не будет отброшена последняя ступень ракеты-носителя и не останется один лишь полезный груз (это может быть посадочный модуль со своими двигателями, но в рамках данной задачи это уже неважно, важна лишь его масса). Каждая ступень состоит из опциональной центральной части (топливные баки и, обычно, двигатель), являющейся частью «ствола» ракеты, и 0, 2, 3, 4 или 6 боковых частей, также состоящих из топливных баков и опционального двигателя под ними. То есть всего возможны три формы ступени:
- только центральная часть (ствол);
- центральная часть + боковые части вокруг него;
- только боковые части.
Третий вариант возможен только при условии, что следующая (по времени работы) ступень — первого типа (только ствол). Фактически, первая и третья форма — это вторая, разбитая на две фазы, где сначала отрабатывают боковые двигатели, отстреливаются, и лишь затем работает центральный.
Каждая часть ступени (центральная или боковые) состоит из 1 — 3 топливных баков, поставленных вертикально друг на друга, и, опционально, двигателя под ними. В ступенях первой и третьей формы двигатели обязаны быть во всех частях. В ступени второй формы, состоящей из центральной части и N боковых, двигателей может быть либо 1 (только в центре), либо N+1 (везде). В пределах одной ступени все топливные баки и все двигатели одинаковые. Число баков во всех частях ступени тоже одинаковое.
В данной задаче используются только Liquid Fuel Engines размера Small и Large, а также топливные баки размера Small и Large. Другие двигатели и баки не используются, всякие твердотопливные бустеры игнорируются.
Программа должна получать на вход два вещественных числа — массу полезного груза в тоннах и бюджет ∆v в м/с. На выход она должна выдать конфигурацию ступеней в порядке сверху-вниз (первой выводится ступень, отрабатывающая позже всех, последней выводится ступень, отрабатывающая раньше всех) в формате JSON-списка. Параметры одной ступени:
fuel— название топливного бака, используемого в этой ступени, строка;engine— название двигателя, строка;central— есть ли в этой ступени центральная часть (true/false);numSideParts— кол-во боковых частей в этой ступени: 0, 2, 3, 4 или 6;numEngines— число двигателей в ступени (число: 1, numSideParts или numSideParts + 1);height— число топливных баков в одной части (1, 2 или 3).
Число ступеней должно быть не больше семи. И сумма высот (числа баков по вертикали) всех ступеней со стволом не должна быть больше семи. Таким образом всего в ракете-носителе может быть максимум семь ступеней единичной высоты. Или две стволовых ступени по 3 бака, одна ступень с одним, и сколько-то чисто боковых. А может быть всего лишь две ступени по два бака, например, то есть общая высота может быть и меньше семи.
Общий запас ∆v для ракеты определяется как сумма ∆v всех ступеней. При расчете ∆v одной ступени следует учитывать, что mstart есть сумма массы полезного груза, массы всех следующих (по времени) ступеней и массы текущей ступени при полных баках. mend — то же, но уже с пустыми баками текущей ступени. Суммарное значение ∆v должно получиться больше или равным заданному на входе требуемому бюджету. При этом следует минимизировать суммарную массу всей ракеты. При расчете ∆v следует брать Isp двигателя в вакууме для всех ступеней кроме стартовой (последняя в выводимом списке), для которой следует использовать значение Isp в атмосфере. Считаем, что первые 5000 м/с бюджета тратятся на подъём с Кербина и выход на его орбиту. Поэтому ступени, работающие на этом участке, обязаны давать тягу такую, которая в невесомости дала бы ускорение 15 м/с2. Тяга для ступени считается как произведение числа двигателей на тягу одного двигателя. Поскольку тяга — это сила, F = m * a, F/m = a, отношение тяги к массе mstart должно быть не меньше 15 для тех ступеней, что дают первые 5000 м/с ∆v. Для последующих ступеней минимально допустимое ускорение равно 5 м/с2, то есть отношение тяги к mstart таких ступеней должно быть не меньше 5.
В игровую физику также входит сопротивление воздуха, но им в этой задаче необходимо пренебречь.
Для участия в конкурсе необходимо было прислать решения, найденные разработанной программой, для следующих параметров:
- m = 10.4, ∆v = 7000 (codename: Mun)
- m = 1.5, ∆v = 12000 (codename: Kerbol)
- m = 11.0, ∆v = 10500 (codename: Moho)
- m = 12.0, ∆v = 14800 (codename: Laythe)
Решение на языке Haskell
В этом разделе кратко описывается решение поставленной задачи, которое подготовил автор и соорганизатор конкурса на языке программирования Haskell (надо отметить, правда, что несмотря на мою переработку и рефакторинг кода, из него всё равно время от времени выглядывают верблюжьи уши). Здесь не будет описываться каждая функция, всякий сможет найти полный модуль по ссылке в конце статьи. Будут представлены наиболее интересные функции с их описанием.
Перво-наперво подключим все необходимые модули:
import Data.Aeson (ToJSON(..), (.=), encode, object)
import Data.ByteString.Lazy.Char8 (unpack)
import Data.Function (on)
import Data.List (sortBy)
import Data.Maybe (fromJust, listToMaybe)
import System.Environment (getArgs)
Здесь мы будем пользоваться форматом JSON, для чего будем использовать готовую библиотеку. Ну и для ускорения расчётов будем проводить их не в режиме интерпретации, а подготовим исполняемое приложение, поэтому пригодится функция получения аргументов командной строки. Остальные модули импортируются по необходимости — какие функции используем, такие модули и импортируем. Хорошим тоном является импорт только тех программных сущностей, которые реально используются в коде (за исключением случаев, когда какой-либо модуль используется массово).
Далее опишем четыре специализированных алгебраических типа данных (АТД), которые необходимы для представления двигателя, топливного бака, структуры ступени и одной ступени соответственно. Все эти АТД будут представлены в виде именованных записей:
data Engine = E
{
eMass :: Double,
thrust :: Double,
isp :: Double,
ispAtm :: Double,
eName :: String
}
deriving Show
data Fuel = F
{
mFull :: Double,
mEmpty :: Double,
fName :: String
}
deriving (Show, Eq)
data StageStruct = SS
{
fuel :: Fuel,
engine :: Engine,
central :: Bool,
sideParts :: Int,
nEngines :: Int,
height :: Int
}
deriving Show
data Stage = S
{
struct :: StageStruct,
mStart :: Double,
mEnd :: Double,
stThrust :: Double
}
deriving Show
Внутреннее содержимое представленных АТД полностью соответствует постановке задачи.
Будет небезынтересным определение экземпляра класса ToJSON (перевод структуры данных в формат JSON) для описания ступени, чтобы можно было выводить это описание в качестве выходного результата работы программы. Вот оно:
instance ToJSON Stage where
toJSON st = let s = struct st
in object ["fuel" .= fuel s,
"engine" .= engine s,
"central" .= central s,
"numSideParts" .= sideParts s,
"numEngines" .= nEngines s,
"height" .= height s]
Теперь перейдём к определени функций. Здесь, как уже было сказано выше, не будут даваться определения всех функций, но только тех, которые необходимы для понимания решения задачи. Вот первая функция, которая требуется для вычисления ∆v заданной ступени при данной массе груза и наличию или отсутствию атмосферы. Возвращает ∆v и общую массу ракеты (груз и эта ступень до начала траты топлива).
calculateStage :: Bool -> Double -> Stage -> (Double, Double)
calculateStage atm pload st = (dV mst mend i, mst)
where
mst = mStart st + pload
mend = mEnd st + pload
i = if atm
then ispAtm eng
else isp eng
eng = engine . struct $ st
А вот функция для определения высоты центральной части ступени:
stemHeight :: Stage -> Int
stemHeight s = let ss = struct s
in if central ss
then height ss
else 0
Теперь напишем функцию поиска самой лёгкой ступени, удовлетворяющей заданным параметрам — наличию атмосферы, возможности использовать чисто боковую ступень, массы груза (куда входит масса более поздних ступеней), требуемого значения ∆v, минимального ускорения, максимально допустимой массы и максимально допустимой высоты центральной части. Она выбирает один из отсортированных списков возможных ступеней (в зависимости от того, можно ли использовать чисто боковую ступень), в нём ищет первую подходящую по параметрам. Перестаёт искать, если дошла в списке до ступеней, которые тяжелее, чем переданное значение mmax — это значит, что ракета с такой тяжёлой ступенью окажется тяжелее, чем какая-то из уже найденных ранее.
stageN :: Bool -> Bool -> Double -> Double -> Double -> Double -> Int -> Maybe (Stage, (Double,Double))
stageN atm possiblyRadial = findStage atm possibleStages
where
possibleStages = if possiblyRadial
then sRadStagesSorted
else stemStagesSorted
findStage atm possibleStages payload targetDV minA mmax avh = listToMaybe good
where
notTooBig = takeWhile (s -> mStart s < mmax) possibleStages
possible = map (s-> (s, calculateStage atm payload s)) notTooBig
good = filter ((s, (dv, m)) -> dv >= targetDV &&
stemHeight s <= avh &&
stThrust s > m * minA) possible
А вот функция поиска оптимальной «программы» (конфигурации — списка ступеней) из двух или более ступеней. Она ищет оптимальную верхнюю ступень с заданным ∆v, и оптимальную «программу» для последующих ступеней, с учётом массы и характеристик найденной оптимальной верхней ступени. Поскольку поиск может закончиться неудачей, результат опциональный, всё работает в монаде Maybe.
splitProgram :: Double -> Double -> Bool -> Int -> Int -> Double -> Double -> Double -> Maybe ([Stage], Double)
splitProgram payload targetDV possiblyRadial nstages avh dv bestFound ddv =
do let minA = if targetDV - dv > 5000
then 5.0
else minAKerbin
(s1, (dv1, m1)) <- stageN False possiblyRadial payload dv minA (bestFound - payload) avh
let avh' = avh - stemHeight s1
let leftTDV = let ldv = targetDV - dv1
in if ldv <= 5000 && minA < 10
then 5000.0
else ldv
(nextStages, mns) <- createRocket m1 leftTDV (stIsStemOnly s1) (nstages - 1) avh' bestFound ddv
return (s1:nextStages, mns)
Следующая функция необходима для выбора лучшей (по массе) конфигурации ракеты из одного или двух вариантов. Используется ниже в процессе поиска для определения текущего лучшего найденного варианта:
chooseProgram :: ([Stage], Double) -> Maybe ([Stage], Double) -> ([Stage], Double)
chooseProgram x Nothing = x
chooseProgram x@(p1,m1) y@(Just (p2, m2)) = if m1 < m2
then x
else fromJust y
Теперь перейдём к определению главной функция поиска оптимальной конфигурации ракеты (или её части) по заданным параметрам: массе груза, бюджету ∆v, возможности начать с чисто боковой ступени (когда вызывается рекурсивно и известно, что более верхняя ступень не имеет боковых частей), числу возможных ступеней (уменьшается при рекурсивном использовании), высоте, массе лучшего найденного решения и шагу ddv перебора ∆v. Искомая ракета должна обеспечивать суммарный бюджет скорости targetDV. Эта функция пробует по-разному распределить этот бюджет между верхней ступенью и всеми остальными. Она перебирает значения ∆v от ddv до targetDV (c шагом ddv), для каждого варианта ищет оптимальную верхнюю ступень, а для оставшегося бюджета ищет оптимальную ракету, вызывая себя рекурсивно.
Лучшее найденное решение запоминается, и его масса используется при поиске для отсечения заведомо более тяжёлых вариантов.
createRocket :: Double -> Double -> Bool -> Int -> Int -> Double -> Double -> Maybe ([Stage], Double)
createRocket payload targetDV possiblyRadial nstages avh bestFound ddv =
let minMass = payload * exp (targetDV / (800 * 9.816))
in if minMass > bestFound
then Nothing
else if targetDV < 500 || nstages == 1
then do st <- stageN True possiblyRadial payload targetDV minAKerbin (bestFound - payload) avh
return ([fst st], snd $ snd st)
else let f bst dv = chooseProgram bst $ splitProgram payload targetDV possiblyRadial nstages avh dv (snd bst) ddv
np = foldl f ([], bestFound) [ddv, ddv * 2 .. targetDV]
in if null . fst $ np
then Nothing
else Just np
Вот функция расчёта характеристик ступеней ракеты — по массе груза и списку ступеней вычисляет список их параметров: ∆v, начальной массы и ускорения:
stagesParams :: Double -> [Stage] -> [(Double, Double, Double)]
stagesParams m0 stages =
let atmSts = zip (reverse $ take (length stages) (True : repeat False)) stages
calculateStage2 atm payload st = let (dv, m) = calculateStage atm payload st
in (dv, m, stThrust st / m)
in tail . scanl ((_, m, _) (atm, st) -> calculateStage2 atm m st) (0.0, m0, 0.0) $ atmSts
Наконец, главная исполняемая функция, которая разбирает параметры и запускает поиск ракеты, выводя результат на экран:
main = do argv <- getArgs
case argv of
ms : dv : _ -> let m = read ms :: Double
tdv = read dv :: Double
plan = createRocket m tdv False 7 7 9999 (tdv / 30)
in putStrLn $ maybe "nope" (present m) plan
_ -> putStrLn "ksp mass deltaV"
Описание программы в целом окончено. Однако необходимо отметить, что для одного из двигателей («Mainsail») в этой программе использовалось другое значение тяги — 1200 вместо 1500, так как в игре на полной тяге этот двигатель перегревается. Но в задаче этот факт всё равно не отражён, и все участники использовали значение 1500. Если в представленной программе значение поменять на 1500, то на решении сказывается тот факт, что оно не учитывает массу разделителей ступеней. Это делает решение проще и обычно не мешает, но именно в данном случае при замене тяги «Mainsail» на 1500 программа находит конфигурацию, которую калькулятор ракет отбраковывает — чуть-чуть другая масса приводит к чуть-чуть другим значениям ∆v и в данном случае меняет требование к ускорению одной из ступеней.
Всякий желающий может получить описанный модуль здесь.
Мои предыдущие статьи о конкурсах по ФП на Хаброхабре:
- Конкурсы в 2011 году: Альманах конкурсов по ФП за 2011 год
- Конкурсы в 2012 году: Альманах конкурсов по ФП за 2012 год
- Игра в «кошки — мышки», поиск минимальной стратегии
- Немного стеганографии: о подготовке апрельского конкурса по ФП
- Июньский конкурс по ФП: поиск закодированной фразы мудреца
- Игра Wordament — реализация помощника на языке Haskell
Автор: Darkus
