В марте ставший уже традиционным ежемесячный конкурс по функциональному программированию начался второго числа. Всем любителям программирования была предложена следующая задача:
У Вас есть два сосуда, один объёмом 5 литров, а другой объёмом 8 литров. Вы можете наливать сосуды до края какой-то жидкостью (будьте осторожны, возможно, что она едкая или ядовитая) из крана. Вы можете выливать жидкость из сосуда в технологическую раковину. Вы можете переливать жидкость из сосуда в сосуд так, что либо в первом сосуде закончится жидкость, либо второй наполнится до краёв (что произойдёт ранее). Ваша задача — отмерить 2 литра жидкости.
Для начала надо понять, а каким это образом можно решить подобную задачу? Если поразмыслить, на ум приходит такой вариант. Из доступных операций имеются только следующие:
- Наливание жидкости в сосуд до краёв (невозможно налить некоторое заданное количество жидкости, потому что на сосудах нет маркировки промежуточных объёмов).
- Переливание жидкости из сосуда в сосуд пока либо в том, из которого переливают, не закончится жидкость, либо тот, в который переливают, наполнится полностью. И это единственный способ отмерять объёмы, не равные исходным объёмам сосудов.
- Опорожнение какого-либо сосуда полностью (поскольку опять же нет маркировки промежуточных объёмов).
Также есть два пути измерения — переливать из большего сосуда в меньший, либо переливать из меньшего в больший. Оба эти способа, в принципе, тождественны друг другу, поскольку просто выполняют одни и те же действия, только в противоположных порядках. Комбинировать действия этих способов смысла нет, поскольку мы просто будем переходить туда-сюда по графу состояний. А граф состояний представляет собой просто закольцованую цепочку переходов, которую проще всего пояснить при помощи следующих диаграмм:
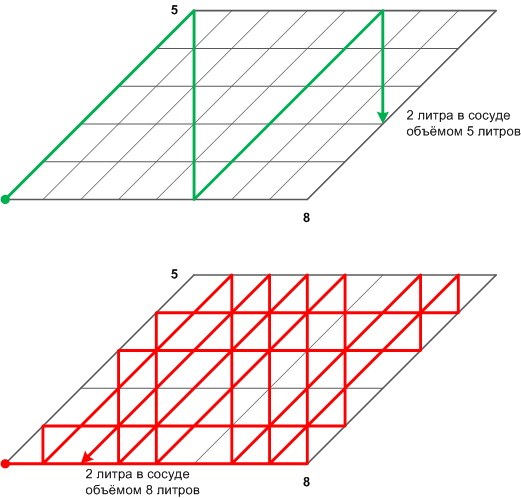
Здесь зелёным путём показано переливание из пятилитрового сосуда в восьмилитровый, а красным путём — из восьмилитрового в пятилитровый. Видно, что первый способ даёт 4 операции: налить жидкости в пятилитровый сосуд, перелить в восьмилитровый, потом опять налить в пятилитровый и снова перелить в восьмилитровый (3 литра). Таким образом, в пятилитровом сосуде останется ровнёхонько 2 литра, что и требуется.
По условиям конкурса надо было ещё осуществить вывод алгоритма переливаний на естественном языке, при этом алгоритм должен состоять из минимального числа шагов. Это было совсем несложно и представляло собой скорее свистелку, чем что-то полезное, однако большинство конкурсантов выполнили и это требование. Посмотрим и мы, как всё это можно реализовать на языке программирования Haskell. Для начала, как всегда, определяем модуль:
> module Liquids where
После этого, опять же как обычно, импортируем пару модулей и функций из них из стандартной поставки.
> import Data.Function (on)
> import Data.List (intercalate)
С функцией on мы уже неоднократно встречались, очень полезная функция, когда встречаются паттерны вроде f x `op` f y. В этом случае хорошо записывать такое выражение как (op `on` f) x y, и это читается как «операция op применяется к результатам применения функции f». Обычно такой подход используется при определении функций в бесточечной нотации, когда аргументы x и y пропускаются.
А вот функция intercalate является простым синонимом для композиции функций concat и intersperse. Последняя перемежает заданный список значений заданным значением, а функция concat сливает внутренние списки в один. Так вот функция intercalate потребуется нам, когда мы будем выводить алгоритм решения задачи в виде строки.
Далее. Определим основной тип данных для представления операций по переливанию. Как было сказано выше, таких операций всего три. Вот мы их и закодируем при помощи алгебраического типа данных:
> data Measurement a = Filling (a, a) a
> | Pouring (a, a) a a
> | Emptying (a, a) a
Первый конструктор представляет наливание жидкости в сосуд, второй — переливание из сосуда в сосуд, а третий — опорожнение сосуда соответственно. Пара в каждом конструкторе будет использоваться для хранения информации о том, сколько жидкости остаётся в обоих сосудах. Решение, конечно, не ахти какое, ибо в данном случае лучшим вариантом было бы использование монады State для таскания состояния из функции в функцию.
А вот теперь сразу определим для этого АТД экземпляр класса Show, и он как раз будет использоваться для вывода в строку (и далее на экран) алгоритма всех этих переливаний. Делается это так:
> instance Show a => Show (Measurement a) where
> show (Filling v m) = showPair v ++ "Налить жидкость из крана в сосуд объёмом " ++
> show m ++ " л."
>
> show (Pouring v m n) = showPair v ++ "Перелить жидкость из сосуда объёмом " ++
> show m ++ " л. в сосуд объёмом " ++ show n ++ " л."
>
> show (Emptying v n) = showPair v ++ "Вылить жидкость из сосуда объёмом " ++
> show n ++ " л."
Функция showPair является служебной и предназначена для преобразования пары в строку. Определяется она так:
> showPair :: Show a => (a, a) -> String
> showPair (mn, mx) = "[" ++ show mn ++ ", " ++ show mx ++ "]: "
Ничего сложного. Специальная такая функция, место которой в замыканиях. Но поскольку она используется в трёх клозах одной и той же функции show, в качестве замыкания её определить невозможно.
Теперь перейдём непосредственно к решению поставленной задачи в общем виде. Мы, естественно, не будем кодировать в программе числа 5 и 8, поскольку их будем принимать на вход в качестве параметров. Вот определение главной функции solve:
> solve :: Int -> Int -> Int -> IO ()
> solve = (((putStrLn . tryNull . zipWith zipper [1..]).).) . getMeasurements
> where
> zipper i d = "Шаг " ++ show i ++ ". " ++ show d
>
> tryNull xs | null xs = "Задача не имеет решения."
> | otherwise = intercalate "n" xs
Опять бесточечная нотация и сечения композиции. Однако тем, кто уже читал мои предыдущие статьи (см. список в конце этой заметки), такая запись уже будет не страшна. Здесь вызывается функция getMeasurements, которая получает на вход три аргумента (поэтому и имеет место двойное левое сечение композиции). Этими тремя аргументами являются объёмы имеющихся в наличии сосудов, а также потребный объём, который необходимо отмерить. Далее полученный список шагов сшивается с бесконечным списком натуральных чисел, причём для сшивки используется локальная функция zipper. Эта сервисная функция переводит шаг переливаний в строку при помощи определённого выше экземпляра класса Show, присоединяя к ней в начале номер шага переливания. Получается список строк, который передаётся на вход локальной функции tryNull. Она проверяет, не является ли он пустым, и если является, то в качестве результата возвращает строку с сигналом о том, что задача не имеет решения. Если же список шагов не пуст, то он сшивается в одну строку при помощи рассмотренной ранее стандартной функции intercalate, причём все строки с описанием шагов перемежаются переводом строки. Всё это добро (уже одна строка, кстати) передаётся на вод стандартной функции putStrLn, которая выводит строку на экран. Всё просто.
Теперь перейдём к функции getMeasurements. Как ясно из предыдущего определения, она должна получать на вход объёмы (двух сосудов и потребный), а возвращать список действий. И она предполагает, что изначально оба сосуда пусты. Посмотрим на её определение:
> getMeasurements :: Int -> Int -> Int -> [Measurement Int]
> getMeasurements m n k
> | m <= 0 || n <= 0 = []
> | k <= 0 || k > mx = []
> | d > 1 && k `mod` d /= 0 = []
> | otherwise = let mf = measureForward ((mn, 0), (mx, 0)) k
> mb = measureBackward ((mn, 0), (mx, 0)) k
> in if ((<=) `on` length) mf mb
> then mf
> else mb
> where
> d = gcd m n
> mn = min m n
> mx = max m n
Недурно, конечно. Охранные выражения, выражения let и замыкания where. Что же это? Замыкания d, mn и mx просто определяют часто встречающиеся в коде этой функции выражения. Для вычислений нам нужен наименьший общий делитель (gcd), минимальный и максимальный объёмы сосудов (так мы их просто отсортируем, чтобы их можно было бы передавать в произвольном порядке). Первые три охранных выражения определяют граничные случаи, когда решений нет. Само собой разумеется, решений нет, когда задаются отрицательные объёмы, либо когда потребный объём больше максимального объёма среди двух сосудов (с этим, конечно, можно немного поспорить, но пусть будет так, поскольку получение объёма от mx до mx + mn в целом тривиально и оставляется в качестве дополнительного упражнения пытливым читателям). Третье охранное выражение не такое тривиальное. Но по представленным ранее диаграммам можно понять, что задача не имеет решения, если объёмы двух сосудов представляют собой взаимно непростые числа, а потребный объём не делится нацело на НОД объёмов двух сосудов. Это можно доказать математически, но опять же дело это оставляется в качестве разминки ума читателям.
Если все три охранных условия успешно пройдены, то ищется решение. Для этого используются две функции: measureForward и measureBackward. Они представляют два способа наливания, о которых говорилось ранее и которые представлены на диаграммах. Собственно, минимальное количество шагов по переливанию и выбирается при помощи сравнения длин списков шагов (использование выражения ((<=) `on` length)).
Так что перейдём к определению функций measureForward и measureBackward. Вот они:
> measureForward :: ((Int, Int), (Int, Int)) -> Int -> [Measurement Int]
> measureForward ((mn, mn'), (mx, mx')) k
> | mn' == k || mx' == k = []
> | mn' == 0 = Filling (mn, mx') mn :
> measureForward ((mn, mn), (mx, mx')) k
> | mn' == mn && mx - mx' >= mn' = Pouring (0, mx' + mn') mn mx :
> measureForward ((mn, 0), (mx, mx' + mn')) k
> | mn' == mn && mx - mx' < mn' = Pouring (mn - (mx - mx'), mx) mn mx :
> measureForward ((mn, mn - (mx - mx')), (mx, mx)) k
> | mx' == mx = Emptying (mn', 0) mx :
> measureForward ((mn, mn'), (mx, 0)) k
> | otherwise = Pouring (0, mn') mn mx :
> measureForward ((mn, 0), (mx, mn')) k
>
> measureBackward :: ((Int, Int), (Int, Int)) -> Int -> [Measurement Int]
> measureBackward ((mn, mn'), (mx, mx')) k
> | mn' == k || mx' == k = []
> | mn' == mn = Emptying (0, mx') mn :
> measureBackward ((mn, 0), (mx, mx')) k
> | mx' == 0 = Filling (mn', mx) mx :
> measureBackward ((mn, mn'), (mx, mx)) k
> | mx' >= mn - mn' = Pouring (mn, mx' - (mn - mn')) mx mn :
> measureBackward ((mn, mn), (mx, mx' - (mn - mn'))) k
> | mx' < mn - mn' = Pouring (mn' + mx', 0) mx mn :
> measureBackward ((mn, mn' + mx'), (mx, 0)) k
> | otherwise = Pouring (mx', 0) mx mn :
> measureBackward ((mn, mx'), (mx, 0)) k
Тут просто закодированы различные варианты состояний системы из двух сосудов. Например, в функции measureForward если в каком-либо из сосудов набирается потребный объём жидкости, то рекурсия останавливается. Если сосуд меньшего объёма пуст, то его надо налить полностью, и т. д. Рассматривать все охранные выражения обеих функций смысла нет, поскольку каждый может пройтись по диаграммам и проверить правильность охранных выражений. Кстати, надо отметить, что их порядок крайне важен, и это можно увидеть, сравнив обе функции.
Обе функции принимают на вход пару, обоими элементами которой являются также пары. Первая пара представляет собой максимальный и текущий объём минимального сосуда, а вторая — то же самое для максимального сосуда. Тоже не очень себе решение, но городить новый АДТ ради этого тоже было бы нецелесообразно.
Для проверки общности реализованных алгоритмов участникам конкурса было предложено найти решение обратной задачи, а именно: «Сколько литров надо попытаться отмерить при помощи сосудов объёмами 1010 и 1011 литров, чтобы минимальное количество шагов измерения равнялось 2012?». Некоторые занудные читатели начали возмущаться, некоторые не смогли организовать перебор для поиска ответа на обратную задачу, поскольку их функции работали очень медленно, и для решения обратной задачи потребовалось бы время, большее времени жизни Вселенной. Но большинство участников стоически выдержали и это испытание. А вот и моя функция для этого:
> testGenerality :: Int
> testGenerality = head [i | i <- [1..1011], length (getMeasurements 1010 1011 i) == 2012]
А вот диаграмма вызовов функций:
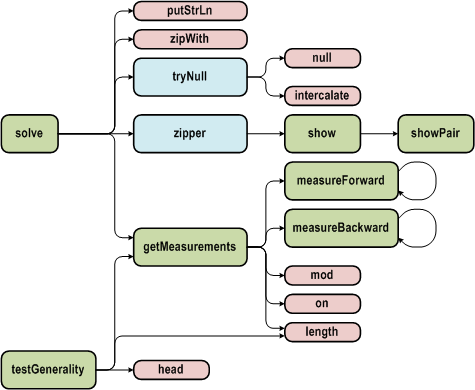
На ней зелёными прямоугольниками показаны реализованные функции, синими — локальные функции (кроме тех, что определены в функции getMeasurements), а красным — функции из стандартных модулей. Не показаны всякие операции типа (<=) и (++), поскольку это также загромоздило бы диаграмму.
Осталось написать, каковы результаты работы написанных функций. Вот результат решения поставленной в конкурсе задачи:
solve 5 8 2
Шаг 1. [5, 0]: Налить жидкость из крана в сосуд объёмом 5 л.
Шаг 2. [0, 5]: Перелить жидкость из сосуда объёмом 5 л. в сосуд объёмом 8 л.
Шаг 3. [5, 5]: Налить жидкость из крана в сосуд объёмом 5 л.
Шаг 4. [2, 8]: Перелить жидкость из сосуда объёмом 5 л. в сосуд объёмом 8 л.
А вот результат проверки общности:
507
Наконец, надо упомянуть, что текст данной статьи представляет собой исходный код на языке Haskell в так называемом литературном стиле. Еси вы скопируете весь текст в файл с расширением .lhc (и не забудьте про кодировку, она должна быть UTF-8), то компилятор GHC с удовольствием откомпилирует этот модуль для вас. Ну или взять полноценный модуль можно здесь.
Вдумчивым читателям предлагаются для самостоятельной проработки следующие задачи:
- Использовать монаду
Stateдля таскания состояния сосудов из функции в функцию. - Использовать монаду
Writerдля вывода алгоритма переливаний. Соответственно для двух монад надо использовать трансформатор. Как это сделать, написано в моей статье про N-граммы. - Доказать, что в функции
getMeasurementsнет смысла находить минимальный и максимальный объёмы сосудов, всё будет прекрасно работать и без этого. - Обобщить алгоритм поиска шагов для переливаний на произвольное количество сосудов. Для подсказок можно воспользоваться решениями конкурсантов, некоторые из которых обобщены подобным образом.
- Построить математически безупречное доказательство того, что для двух сосудов не существует решения, если объёмы сосудов не представляют собой взаимно простых чисел, а потребный объём при этом не делится нацело на НОД объёмов сосудов.
Если вы хотите дополнительно отблагодарить автора, но не знаете как, то вам сюда.
Мои предыдущие статьи о конкурсах по ФП на Хаброхабре:
- Решение задачи о перегорающих лампочках на языке Haskell
- Фреймворк для решения задач о переправах на языке Haskell
- Конструирование и вычисление арифметических выражений на языке Haskell
- Расшифровка кода на языке Haskell (конкурс по ФП в январе 2012)
- Шахматные задачи на мат в один ход: решение на языке Haskell
Автор: Darkus






