Полиморфия и классы в Haskell

Здравствуй, дорогой читатель!

Cегодня мы поговорим о полиморфизме функций и о классах в языке Haskell, как их использовать и для чего они нужны. Все мы использовали метод полиморфизма, например, в языке Java. А как это можно применить к Haskell? Haskell не является объектно-ориентированным языком, но в нём всё же присутствуют классы. Хотя классы в Haskell и имеют некоторые свойства классов объектно-ориентированных языков, они более абстрагированы и от этого намного мощнее. Проводя аналогию с языком Java дальше, классы в Haskell являются ничем другим как интерфейсы — в класс записываются лишь декларации функций, а сами реализации этих функций будут сделаны позже.
Хочется выразить благодарность пользователю Darkus за прочтение и исправление всех недочётов и неточностей в статье, а также за дельные советы и помощь в написании.

Полиморфизм функций

В Haskell существует два вида полиморфизма — параметрический и специальный (в английском языке называют термином «ad hoc», который пришел из латинского языка).

Параметрический

Если вы хоть раз программировали на языке Haskell, то непременно встречали примеры параметрического полиморфизма в функциях length, head, teal, curry, uncurry, map, filter, .... Что объединяет все эти функции? Давайте посмотрим на реализацию некоторых из них:

length :: [a] -> Int
length []	= []
length (_:xs) 	= 1 + length xs

head :: [a] -> a
head (x:_) = x

tail :: [a] -> [a]
tail (_:xs) = xs

curry :: ((a,b) -> c) -> (a -> b -> c)
curry f x y = f (x,y)

uncurry :: (a -> b -> c) -> ((a,b) -> c)
uncurry g (x,y) = g x y

У первых трёх функций входной параметр типа a, а у curry и uncurry еще b и c. Вместо конкретного типа данных (Int, Bool, Char,...) используется типизация. Пример на java:

public class Test<A> {...}

Здесь тоже используется А — неизвестный тип данных, который будет определён во время компиляции. Полиморфизм используется тогда, когда неизвестно какого типа данных будет параметр, но известны операции, которые над ним (илм с ним) будут производиться.

Все идентификаторы типовых переменных в языке Haskell должны начинаться с маленькой буквы (например a, abc, aA101), а все конкретные типы (конструкторы) начинаются с большой буквы (например String, Int, Node).

Параметр a может принимать любые типы, будь то Int, String или даже функции (например, length [f, g, h], где f, g, h — функции, которые имеют одинаковые типы). Стоит заметить, что тип b может также принимать любые типы, в том числе и тип параметра a.

Тип функции в интерпретаторе GHCi (и в Hugs) всегда можно узнать с помощью команды :t, например:

Main>:t length
length :: [a] -> Int

Специальный (ad hoc)

Синонимом специального полиморфизма является термин «перегруженные функции». Это более слабый тип полиморфизма, чем параметрический. Возьмём для примера оператор (функцию) сложения (+). Выражения такого вида
(+) 2 3 ->> 5
(+) 2.5 3.85 ->> 6.35
отличаются от выражений
(+) True False
(+) [1,2,3] [3,2,1]
тем, что в первом случае были использованы численные значения, а во втором значения типа Bool и [Int]. Оператор сложения не определён для нечисленных типов. Всё потому, что эта функция имеет тип не
(+) :: a -> a -> a
а такой
(+) :: Num a => a -> a -> a. То есть здесь вводится ограничение на тип вводимых (и выводимых) данных.

Ограничение, которое наложено на тип a: Num a говорит, что тип a должен быть элементом класса Num. Такие классы типов очень важны в Haskell, так как они добавляют дополнительную защиту от ошибок при программировании, а также могут уменьшить количество написанного кода в разы. Это мы увидим в следующем примере.

Даны следующие типы двоичных деревьев:
Двоичное дерево, которое может хранить любой тип данных

data Tree1 a = Nil | Node1 a (Tree1 a) (Tree1 a)

Двоичное дерево, которое может хранить два элемента, и каждое ответвление оканчивается «листом» c одним элементом (а не Nil):

data Tree2 a b = Leaf2 b | Node2 a b (Tree2 a b) (Tree2 a b)

Двоичное дерево, которое может хранить данные типа String и тоже оканчивается листом:

data Tree3 = Leaf3 String | Node3 String Tree3 Tree3

И, скажем, есть еще два вида списков:
обычный

type Lst a = [a]

и тип “верёвка”

data Rope a b = Nil | Twisted b (Rope b a)

Имея все эти структуры данных, хотелось бы написать функцию size, которая независимо от структуры данных, выводила бы либо её глубину (для деревьев), либо длину (для списков), или одним словом — размер. Наивным решением было бы написать для каждого свою функцию:

sizeT1 :: Tree1 a -> Int --считаем кол-во узлов
sizeT1 Nil		= 0
sizeT1 (Node1 _ l r) 	= 1 + sizeT1 l + sizeT1 r

sizeT2 :: (Tree2 a b) -> Int --считаем кол-во элементов
sizeT2 (Leaf 2 _)	= 1
sizeT2 (Node2 _ _ l r)	= 2 + sizeT2 l + sizeT2 r

sizeT3 :: Tree3 -> Int --считаем длины элементов типа String
sizeT3 (Leaf3 m)= length m
sizeT3 (Node m l r)	= length m + sizeT3 l +sizeT3 r

-- и для списков:
sizeLst :: [a] -> Int
sizeLst = length

sizeRope :: (Rope a b) -> Int
sizeRope Nil			= 0
sizeRope (Twisted _ ls)	= 1 + sizeRope ls

Теперь если появится еще какая-нибудь структура данных, то придется делать новую функцию, которая будет подходить только для этой структуры. А нам хотелось бы, чтобы одной функцией можно было получить размер любой структуры данных. Как у функции (+) было ограничение классом Num, так и нам надо сделать ограничение классом Size, а для этого надо его сначало создать:

class Size a where
	size :: a -> Int

Осталось только сделать экземпляры (инстанции) этого класса под конкретные значения a (=под конкретные типы данных):

instance Size (Tree1 a) where
	size Nil		= 0
	size (Node1 _ l r)	= 1 + size l + size r
	
instance Size (Tree2 a b) where
	size (Leaf2 _)		= 1
	size (Node2 _ _ l r)	= 2 + size l + size r
	
instance Size Tree3 where
	size (Leaf3 m)	= length m
	size (Node3 m l r)	= length m + size l + size r
	
instance Size [a] where
	size = length

instance Size (Rope a b) where
	size Nil	 	= 0
	size (Twisted _ ls)	= 1 + size ls

Готово! Теперь если мы в GHCi напишем :t size, то увидим size :: Size a => a -> Int. Мы получили что хотели:

size Nil ->> 0
size (Node1 "foo" (Node1 "bar" Nil Nil) Nil) ->> 2
size (Leaf 2 "foo") ->> 1
size (Node3 "foo" (Node3 "bar" (Leaf3 "abc") (Leaf "cba")) (Leaf "tst")) ->> 15 --3*5
size [1..5] ->> 5
size (Rope 2 (Rope ‘a’ (Rope 5 Nil))) ->> 3

Каждый экземпляр класса Size реализовал функцию size, которая применима лишь к значениям определённого типа (=структурам данных). В данном случае эта функция, как и другие предопределённые операторы (+), (*), (-), перегружена.

Но есть и свои минусы у такого решения. Например, нам бы хотелось узнать количество элементов в парном списке, то есть

size [(1,2), (3,4)] ->> 4
size [('a','b'), ('c','d'), ('e','f')] ->> 6 

Очевидно было бы сделать следующее:

instance Size [(a,b)] where
	size = (*2) . length

Но здесь у нас возникнет проблема, из-за того у нас уже есть инстанция для обычного списка (instance Size [a] where), нам более нельзя использовать другое определение, потому что, как уже говорилось ранее, тип a может быть любым типом, в том числе и (b,c), то есть. [a] == [(b,c)] Для решения данной проблемы можно использовать Overlapping Instances (англ. перекрывающие экзепляры класса). У этого решения есть и свои минусы (импорт одного из модулей может поменять значение программы, может вызвать сбивающие с толку ошибки, и так далее).
Теперь немного подробнее о классах.

Классы

В предыдущем примере мы сдалали класс Size, а вот неполная декларация класса в Haskell: (tv = type variable):

class Name tv where
	сигнатура включающая переменную tv

Неполная потому, что в декларацию класса также могут быть введены ограничения на tv (например, tv должна быть элементом класса Ord). Сигнатур может быть сколько угодно, но каждая из них должна включать (как входной и/или выходной параметр) переменную tv.
Типовые классы — это коллекции типов, для которых определены специальные функции. Вот некоторые (одни из важнеших) классы в Haskell:

• Eq — класс для теста на равенство (неравенство) двух типов данных (операции ==, /=)
• Ord — класс для определения порядка типов, то есть какой элемент больше, какой меньше (операции >, >=, <, <=, min, max...)
• Enum — класс для типов, чьи значения можно «посчитать» (например, [1..10])
• Bounded — класс тоже используется для типов класса Enum. Используется для наименования низжшей и высшей границы типа.
• Show — класс для типов, значения которых можно преобразовать в строку, (=можно представить как символы)
• Read — класс для типов, значения которых можно преобразовать из строки

Только эти классы можно автоматически наследовать любому типу данных (= поместить в секцию deriving). Между классами существует тоже зависимость. Например, если мы знаем как сравнивать два элемента (класс Ord), то мы должны заранее уметь определять равен ли один элемент другому (класс Eq). Ведь для реализации оператора (>=) надо иметь реализованный оператор (==). Поэтому, можно сказать, что класс Ord зависит (наследует) от класса Eq. Вот более подробная схема зависимости классов:

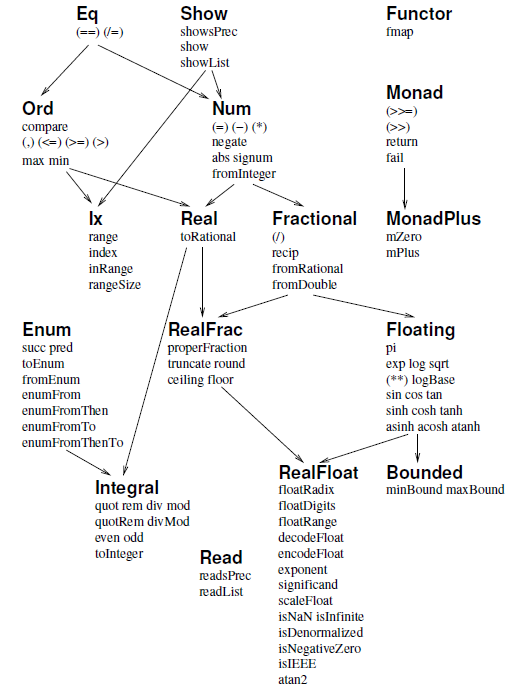
Давайте посмотрим на класс эквивалентности Eq более детально. Как уже ранее было упомянуто, этот класс должен иметь две функции (==) и (/=):

class Eq a where
	(==), (/=) :: a -> a -> Bool --так как сигнатуры (==) и (/=) одинаковы, их можно записать в 1 строчку
	x /= y = not (x == y)
	x == y = not (x /= y)

Из кода видно, что для любой инстанции класса Eq, достаточно реализовать одну из двух функций. Например, для типа Bool (два типа равны лишь тогда, когда они оба True или False) это сделано следующим образом:

instance Eq Bool where
	(==) True True		= True
	(==) False False 		= True
	(==) _ _			= False 

Как видно, случай True False и False True (так же как и последнюю строку) не обязательно писать, т.к. неравенство является обратной операцией равенства. Если до этого у нас было так, что тип является кокретизацией другого типа (например, [Int] является инстанцией типа [a]), то теперь тип может являться экземпляр класса (например, Bool является инстанцией класса Eq). По этой же аналогии, можно написать функции равенства тех двоичных деревьев, что мы использовали выше. Например, для Tree2:

instance (Eq a) => Eq (Tree2 a) where --накладываем условие на a, что этот тип может сравниваться
	(==) (Leaf2 s) (Leaf2 t)		= (s==t)
	(==) (Node2 s t1 t2) (Node2 t u1 u2)= (s==t) && (t1 == u1) && (t2 == u2)
	(==) _ _				= False

Для (Tree3 a b) мы уже должны будем накладывать условие как на a, так и на b, то есть
instance (Eq a, Eq b) => Eq (Tree3 a b)

Всё что левее символа => называется контекстом, всё что правее этого символа должно быть либо базовым типом (Int,Bool,...), либо конструкторы типов (Tree a, [...],...). Оператор (==) является перегруженной функцией (ad-hoc полиморфия).

Равенство (==) является типозависимым свойством, которое требует реализации под каждый тип (как например реализация равенства двоичных деревьев). Хотелось бы, чтобы можно было сравнивать две функции таким образом:

(==) fac fib ->> False --где fac - факториал числа, а fib - число Фибоначчи
(==) (x -> x+x) (x -> 2*x) ->> True
(==) (+2) (2+) ->> True

Это требовало бы в Haskell написания такого кода:

instace Eq (Int -> Int) where
(==) f g = ... --где f и g являются какими-то функциями

Возможно ли написать такую функию, которая бы выдавала результат равенства двух любых функций (True или False)? К сожалению, из тезиса Чёрча-Тьюринга следует, что равенство двух любых функций нельзя определить. Не существует алгоритма, который бы для двух любых данных функций, всегда и через конечное количество шагов решал, являются ли две функции равными или нет. Такой алгоритм нельзя запрограммировать ни на одном языке программирования.

Вместо реализации своей функции для равенства, например двоичных деревьев, можно всегда поместить те классы, которые наследуются данным типом автоматически после ключевого слова deriving. То есть мы могли бы вполне спокойно написать:

data Tree a = Nil | Node a (Tree a) (Tree a) deriving Eq

Это позволяет нам не писать собственноручно инстанцию класса Eq (instance Eq a => Eq (Tree a) where ...). Но для любой функции, тогда придется накладывать условие на переменную a, что эта переменная является элементом класса Eq. Иногда, всё-таки приходится самому писать эти функции, так как «автоматическое» сравнение не всегда работает так как мы бы того хотели. Например для двоичного дерева

data Tree3 a b = Leaf3 bl | Node3 a b (Tree3 a b) (Tree3 a b) deriving Eq

будет реализована (автоматически) следующая функция:

instance (Eq a, Eq b) => Eq (Tree3 a b) where
(==) (Leaf3 q) (Leaf3 s) 			= (q==s)
(==) (Node3 _ q t1 t2) (Node3 _ s u1 u2)	= (q==s)&&(t1==u1)&&(t2==u2)
(==) _ _					= False 

Как мы видим, первый аргумент Node3 был опущен, чего нам бы не хотелось в некоторых случаях.

Заключение

Неформальное отличие двух типов полиморфии:

• параметрическая — один и тот же код независимо от типа.
• ad-hoc — разный код, хотя одинаковые имена функций.

Автор: IvanP

Источник