Сегодня я хотел бы рассказать про ноябрьский конкурс по функциональному программированию, несмотря на то, что с момента его проведения уже прошло практически два месяца. Соорганизатором конкурса выступил наш уважаемый коллега Алексей Кишкин, который предложил задачу, реализовал её решение на нескольких языках программирования, а также подготовил некоторую вспомогательную инфраструктуру для проверки решений.
Задача на кункурс была вынесена крайне известная. Необходимо было решить банальную проблему раскраски карты, то есть поиска хроматического числа графа. Предполагалось, что конкурсанты представят на суд общественности общее решение, которое они проверяли на задаче раскраски карты России на уровне субъектов федерации. Ну и так вышло, что задача, несмотря на свою известность и давнишность, заинтересовала многих участников, так что на конкурс были присланы решения на многих языках программирования.
Ну а мы, как обычно, далее в этой краткой заметке мы рассмотрим решение указанной задачи на языке программирования Haskell. Впрочем, я сразу хочу оговориться — программа написана соорганизатором конкурса, который обычно пишет свои программы на языке OCaml, так что сегодня, как я ни старался, в определениях функций мы будем постоянно видеть торчащие верблюжьи уши OCaml'я :).
Алгоритм
Не мудрствуя лукаво, воспользуемся уже известным алгоритмом раскраски графов, который основан на подходе с использованием метода неявного перебора. Работа этого алгоритма подразделяется на две последовательные фазы.
Во время первой фазы строится начальная допустимая раскраска графа по следующему правилу — первая вершина красится в первый цвет, а далее для каждой вершины выбирается такой минимальный по номеру цвет, чтобы никакая из смежных с данной ранее окрашенных вершин не имела этого цвета.
Во время второй фазы, если это возможно, достигается «лучшая» раскраска, использующая меньшее число цветов. На первом шаге второй фазы отыскивается первая по номеру вершина, окрашенная в цвет, от которого мы хотим избавиться. И из неё осуществляется так называемый шаг возвращения, а именно — во множестве вершин, смежных с данной, с меньшим чем у неё номером, находим максимальную (она была окрашена позже остальных, пусть это N-ая вершина) и пытаемся перекрасить её в другой допустимый цвет с номером большим её собственного, но меньшим номера «лишнего» цвета. Если это удаётся, то далее по правилу первой фазы перекрашиваются следующие вершины с (N + 1)-ой до конца. Если ни одна из них не потребует цвета, от которого мы избавляемся, значит мы добились оптимальной раскраски с меньшим количеством цветов и остановимся.
А если какая-то вершина потребует — мы осуществляем шаг возвращения из неё. В ситуации, когда та самая N-ая вершина не может быть перекрашена в другой допустимый цвет — сразу же делаем шаг возвращения из неё. Алгоритм завершает работу, если на шаге возвращения достигается первая вершина.
Как видно, во время такого перебора вершин осуществляется движение по дереву поиска в глубину. Несмотря на то, что алгоритм переборный, он нисколько не хуже других известных методов и вполне эффективен.
Реализация
Начнём с определения типов данных. Это всё будут только синонимы, и это более или менее просто:
type RegionNumber = Int
type Color = Int
type Regions = Map RegionNumber [RegionNumber]
type Picture = Map RegionNumber Color
Здесь у нас два раза переобозначается тип Int, которым мы кодируем номера цветов и номера регионов на карте. Что-то иное использовать в этом деле — себе дороже, поскольку цвета даже в алгоритме кодируются целыми числами, а для кодирования регионов вполне достаточно использовать номер региона, хотя можно было бы использовать его код в виде строки. Но это немного замедлило бы само решение, а для больших карт такое замедление было бы критичным. Так что оставим так.
Тип Regions представляет собой перечень соседних регионов для заданного. Вся эта информация хранится в словаре (Map), причём кодом является номер региона, а значением — список тех регионов, с которым граничит регион, чей номер является кодом. В свою очередь, вся карта тоже является словарём, но в нём в качестве кода также хранится номер региона, а в качестве значения — номер цвета.
Перейдём к определению функций и начнём с самого верха. Вот определение функции main:
main fn = do
s <- readFile fn
let fileData = map loadData $ lines s
names = zip [1..] $ map fst fileData
codes = Map.fromList $ map ((a, b) -> (b, a)) names
nodes = foldl (acc (x, nl) -> Map.insert (codes Map.! x)
[codes Map.! n | n <- nl] acc) Map.empty fileData
solution = paint nodes 1 Map.empty
nsl = optimizeLoop nodes solution $ numberOfColors solution
if validPicture nodes nsl
then printSolution nsl $ Map.fromList names
else putStrLn "ОШИБКА: Некорректный результат работы программы."
Ну тут всё просто. Сначала мы загружаем весь файл в память и проводим его первичную обработку при помощи функции loadData. Она для каждой строки файла возвращает пару вида (регион, список граничащих с ним регионов). Затем список таких пар преобразуется в структуру данных, содержащую не идентификаторы регионов, а их номера (за это отвечают строки, в которых рассчитываются образцы codes и nodes). После этого проводится первая фаза описанного ранее алгоритма при помощи вызова функции paint. Результат её работы передаётся во вторую фазу алгоритма, в функцию optimizeLoop. После этого делается проверка того, что полученная раскраска карты валидна, и в случае успешного прохождения проверки на экран выводится решение.
Вот определение функции loadData, осуществляющей первичную обработку файла с данными:
loadData :: String -> (String, [String])
loadData l =
case splitOn ":" l of
[rgn, nbrs] -> (rgn, filter (n -> length n > 0) $ splitOn " " nbrs)
_ -> error "ОШИБКА: Некорректный формат входного файла."
Как видно, здесь вовсю используется функция splitOn из модуля Data.List.Split, который необходимо подключить, предварительно установив пакет split. Этот модуль содержит функции, использующиеся для разделения списков по различным критериям. В частности, функция splitOn берёт список и возвращает список списков, полученных при помощи разделения исходного списка на подсписки при помощи какого-либо заданного элемента. Например, если функции splitOn задан символ (:) и, скажем, строка "moscow: moscowregion, kaluga". В результате функция вернёт список ["moscow", " moscowregion, kaluga"]. Именно на этом свойстве основана функция loadData — сначала строка разделяется на две подстроки по символу (:), а потом второй подсписок разделяется по символу пробела.
Теперь переходим к функции paint, которая раскрашивает карту (на первой фазе алгоритма). Вот её определение:
paint :: Regions -> Color -> Picture -> Picture
paint rgn clr pct = if null np
then pct
else paint rgn (clr + 1) $ paintWith clr rgn pct np
where
np = Set.toList $ Set.difference (Map.keysSet rgn)
(Map.keysSet pct)
Эта функция берёт карту (аргумент pct) и раскрашивает её всеми возможными цветами. При вызове из функции main определяется, что номера цветов пока ничем не граничены, и можно использовать их столько, сколько получится по результатам работы первой фазы алгоритма. В замыкании np рассчитывается список тех регионов, которые ещё не окрашены ни в один цвет. А функция paintWith окрашивает все неокрашенные регионы карты в заданный цвет, если каждый соответствующий регион возможно покрасить в этот цвет (нет соседей этого же цвета). Вот её определение:
paintWith :: Color -> Regions -> Picture -> [RegionNumber] -> Picture
paintWith _ _ pct [] = pct
paintWith clr rgn pct np = case filter validRegions np of
[] -> pct
(r:rs) -> paintWith clr rgn (Map.insert r clr pct) rs
where
validRegions rgn' = case Map.lookup rgn' rgn of
Just n -> all (differentColors clr) n
Nothing -> False
differentColors c r = case Map.lookup r pct of
Just c' -> c' /= c
Nothing -> True
Ну тут всё просто. Ищем среди заданных непокрашенных регионов те, которые можно покрасить в заданный цвет. Это делается при помощи локально определённого предиката validRegions. Если этот предикат находит регионы, то первый из них окрашивается в заданный цвет, а по остальным опять пробегается этой же функцией paintWith, поскольку среди оставшихся неокрашенных регионов могут появиться такие, которые уже нельзя красить в заданный цвет (они граничат с только что покрашенным).
Теперь мы плавно переходим ко второй фазе алгоритма. Она реализована в функции optimizeLoop. Вот её определение:
optimizeLoop :: Regions -> Picture -> Color -> Picture
optimizeLoop rgn pct maxClr =
case optimize rgn pct maxClr of
Just npl -> let newMaxClr = numberOfColors npl
in if newMaxClr >= maxClr
then optimizeLoop rgn npl newMaxClr
else npl
Nothing -> pct
Как даже следует из её названия, эта функция циклически пытается удалить цвет с максимальным номером из раскраски карты. Она делает это при помощи прохода функции optimize, которая либо находит оптимальную раскраску, и тогда в ней берётся максимальный цвет, и ежели он меньше текущего максимального цвета, то цикл оптимизации проходится вновь по новой оптимизированной раскраске. В противном случае мы берём полученную оптимизированную раскраску карты. А ежели функция optimize не может найти оптимальную раскраску, то результатом полагается текущая. Всё.
Переходим к функции optimize:
optimize :: Regions -> Picture -> Color -> Maybe Picture
optimize rgn pct clrToRemove =
case [x | (x, c) <- Map.toList pct, c == clrToRemove] of
[] -> Just pct
toCheck -> stepBack (minimum toCheck) rgn pct clrToRemove
Эта функция как раз реализует первый шаг второй фазы алгоритма — она пытается удалить заданный цвет. Делает она это чётко по алгоритму путём возвращения на шаг назад из региона. Это осуществляет функция stepBack. Вот её определение:
stepBack :: RegionNumber -> Regions -> Picture -> Color -> Maybe Picture
stepBack 1 _ pct _ = Nothing
stepBack node rgn pct clrToRemove = repaint rgn pct clrToRemove $
reverse $
sort $
filter (< node) (rgn Map.! node)
Тут так. Берём список регионов, граничащих с заданным. Фильтруем их так, чтобы их цвет был меньше, чем у заданного региона. Сортируем, обращаем и перекрашиваем. Перекраска осуществляется при помощи функции repain, которая определена следующим образом:
repaint :: Regions -> Picture -> Color -> [RegionNumber] -> Maybe Picture
repaint _ pct _ [] = Nothing
repaint rgn pct clrToRemove (c:cs) =
case repaintWith rgn pct ((pct Map.! c) + 1) clrToRemove c of
Nothing -> repaint rgn pct clrToRemove cs
ok -> ok
Эта функция последовательно пробует перекрасить все заданные регионы при помощи функции repaintWith, которая перекрашивает регионы в заданный цвет (в то время как описываемая функция пытается использовать все возможные цвета, которые доступны — по номеру меньшие, чем номер цвета текущего региона). Вот определение функции repaintWith:
repaintWith :: Regions -> Picture -> Color -> Color -> RegionNumber -> Maybe Picture
repaintWith rgn pct clrFrom clrTo cnd
| clrFrom >= clrTo = Nothing
| otherwise = if validPicture rgn np
then if numberOfColors np < clrTo
then Just np
else optimize rgn np clrTo
else repaintWith rgn pct (clrFrom + 1) clrTo cnd
where
np = paint rgn 1 $
Map.filterWithKey (n _ -> n <= cnd) $
Map.insert cnd clrFrom pct
Тут мы дополнительно проверяем валидность цветов, в случае того, что всё нормально, проверяем валидность раскраски. Если раскраска валидна и при этом номер цвета, в который необходимо перекрасить регионы, меньше, чем максимальное количество цветов в текущей раскраске, то функция вызывает уже рассмотренную функцию optimize, которая пытается оптимизировать раскраску. Если же раскраска получается невалидной, то мы снова пытаемся перекрасить, только увеличиваем номер цвета на один.
Осталось рассмотреть две служебные функции. Первая — numberOfColors. Вот её определение:
numberOfColors :: Picture -> Int
numberOfColors = maximum . map snd . Map.toList
Это тривиальная функция, несмотря на бесточечную нотацию. Она просто возвращает максимальный номер цвета в заданном словаре. Получает на вход словарь, преобразует его в список пар, вычленяет вторые элементы (номера цветов) и берёт максимальное число.
А вот функция validPicture, которая представляет собой предикат, проверяющий валидность раскраски карты:
validPicture :: Regions -> Picture -> Bool
validPicture rgn pct = all (uncurry validRegion) $ Map.toList pct
where
validRegion rgn' clr = all (differentColors clr) (rgn Map.! rgn')
differentColors c r = case Map.lookup r pct of
Just c' -> c' /= c
Nothing -> True
Этот предикат просто проверяет условие того, что ни один регион не имеет соседа, окрашенного в тот же самый цвет. Он пробегается по всем регионам карты и для каждого из них смотрит, есть ли у него соседи, окрашенные в тот же цвет. Если хоть одна такая пара находится, то предикат возвращает значение False.
Всё.
Результаты
Посмотрим, что будет в результате выполнения этой программы. В этом нам поможет сайт, подготовленный соорганизатором как раз для этих целей: Хроматическое число карты. Это крайне специализированный сайт — он расскрашивает только карту России и ничего больше. Однако для проверки решений, которые присылались на конкурс, этого хватит.
Исходные данные для работы надо взять по этой ссылке. Там лежит файл, в котором как раз записано описание административного состава России в том формате, который ранее описан в этой статье. И если этот файл скормить функции main, то мы получим что-то типа следующего:
magadan 3
volgograd 3
altaikrai 3
tuva 2
saratov 2
kaliningrad 1
altai 1
ryazan 1
novgorod 4
penza 4
arkhangelsk 4
kabardinobalkaria 3
moscow 2
tula 4
...
Если затем полученный результат внести в поле вводе на указанном выше сайте, то результатом будет следующая карта:
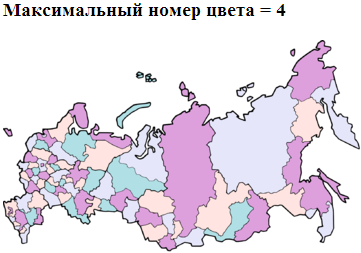
Таким образом были собраны результаты со всех участников конкурса, и сводку по этим результатам можно посмотреть здесь. Кто участвовал, тот — молодец.
Заключение
Всех читателей, как обычно, благодарю за интерес к моим материалам. Всех опять приглашаю к участию в конкурсах по функциональномо программированию — это не только интересно, весело и познавательно, но и можно получить разнообразные призы. Количество и качество призов постоянно растёт, так что конкурсанты всегда довольны.
Описанный модуль на языке Haskell, как обычно, можно получить по следующей сылке: MapPainting.
Мои предыдущие статьи о конкурсах по ФП на Хаброхабре:
- Конкурсы в 2011 году: Альманах конкурсов по ФП за 2011 год
- Расшифровка кода на языке Haskell (конкурс по ФП в январе 2012)
- Шахматные задачи на мат в один ход: решение на языке Haskell
- Измерение объёмов при помощи двух заданных сосудов: решение на языке Haskell
- Трансмутации слов друг в друга: решение на языке Haskell
- Решение арифметических задач — вероятностный подход против регулярных выражений
- Поиск кратчайшего расстояния между точками в трёхмерном пространстве
- Управление лифтами: решение на языке Haskell
- Решение логических задач на языке Haskell: в своём ли уме Валет?
- Поиск скрывающегося Доктора X среди пациентов — решение более сложных логических задач
- Шарики и дырки — один из вариантов плотной упаковки на языке Haskell
Автор: Darkus
