Традиционный конкурс по функциональному программированию, который ежемесячно проводится под эгидой ФП(ФП), в октябре выдался неудачным. Неудачи сопутствовали с самого начала и до конца. Мало того, что вызвавшийся ещё в начале прошедшего лета соорганизатор не смог подготовить задачу, так он ещё и пропал (видимо, как и грозился, уехал на сборы, но не уведомил). А в резерве у меня ничего не было, поэтому пришлось готовить задачу в экстренном порядке. В итоге задача, по всей видимости, показалась потенциальным конкурсантам достаточно сложной — то ли условия были сформулированы кое-как, то ли ещё что. В общем, в конкурсе принял участие всего один человек, который представил решение на языке Haskell, при этом он утверждает, что учил язык специально для этого случая.
Ну а я в недоумении, поскольку сам я реализовал решение на том же самом языке в течение получаса чистого времени, причём решение основано на методе грубой силы, но работает в режиме интерпретации всего полминуты, находя все решения поставленной задачи. Не знаю, как так сошлись звёзды, но пока этот конкурс поставил своеобразный рекорд по участию. Ну а мы давайте перейдём к постановке задачи и описанию решения.
Постановка задачи
Поскольку задачу надо было придумывать срочно, я пошёл за советом к старшему сыну. Он показал мне на свою коллекию головоломок со словами: «Выбирай». Среди всего множества мне особенно приглянулась головоломка, состоящая из шести планок и шариками и дырками в них. Эти планки надо было уложить в два ряда друг на друга и крест-накрест по три планки в каждом ряду. Уложить надо было так, чтобы шарики легли в дырки, ничего не топорщилось и не выпирало. То есть, по сути, это была головоломка на поиск плотной упаковки. Всё дело осталось за реализацией, а дьявол, как известно, прячется именно в деталях. Подразумеваю, что именно этот детальный дьявол и отпугнул конкурсантов, хотя задача и проста, в чём мы сейчас сможем убедиться.
Итак, вот все планки, как они есть:
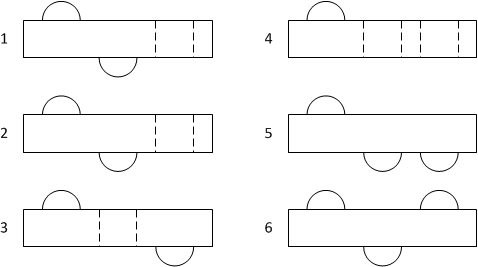
Соответственно, из этих шести планок надо составить пару троек — из первой тройки выкладывается первый уровень, а из второй — второй соответственно. Планки кладутся друг на друга крест-накрест, и шарики утапливаются в дырки. Выглядит это дело следующим образом:
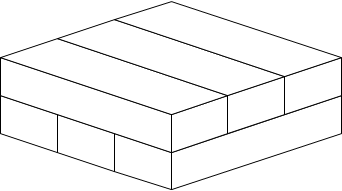
То есть, другими словами, необходимо получить вот такой брусок. Само собой разумеется, что здесь на диаграмме не показаны дырки и шарики на планках, иначе это было бы сразу предоставлением решения.
Реализация
Собственно, здесь ничто не удерживает от использования метода грубой силы. Если я ничего не путаю в комбинаторике, то здесь имеется 46 * 6! комбинаций расположения планок друг относительно друга, в которых учитываются все повороты и отражения правильных решений. Это составляет всего около трёх миллионов комбинаций, что можно перебрать чуть ли не вручную. Скорее всего, именно это послужило тем фактором, который заставил признать задачу неинтересной для конкурсантов.
Так что так и будем решать — подготовим полный список вариантов, после чего банально выберем из него те, которые подходят под условия задачи. То есть основная проблема заключается в реализации комбинаторики. И тут можно даже не заниматься обработкой всех поворотов и отражений, хотя и это можно было бы сделать. Ну-с, начали-с…
Начнём с описания типа, который представляет одну ячейку на планке. Каждая ячейка может быть в одном и только одном из следующих состояний: шарик наверху, шарик внизу и дырка. Других состояний нет. Так что тип будет представлять собой банальное перечисление:
data Cell = Up
| Down
| Hole
deriving Eq
Дополнительно определим два синонима, которые позволят красиво записывать сигнатуры функций. Нам нужны синонимы для представления планки и одного уровня. И тут нас ждёт хороший сюрприз. Я могу сказать, что впервые со времени моей работы с языком Haskell я встречаю реальную необходимость использовать идентификатор Bar в качестве имени типа. И это:
type Bar = [Cell]
type Plane = [Bar]
Тип Bar, то есть «планка», представляет собой банальный список. Можно было бы сделать кортеж из трёх элементов, но такое решение было бы очень узким. А тут — обобщённое. Но обобщение влечёт и неприятность — следить за длинами списков, представляющих планки, придётся вручную. Ну а тип Plane представляет собой один уровень, то есть, по сути, матрицу ячеек. Этим и воспользуемся позже, когда будем поворачивать планки крест-накрест.
Теперь займёмся функциями. Для начала определим функцию, которая возвращает планки исходного задания. Ну и для определённых целей определим константу, которая определяет количество планок в первоначальном задании:
nofBars :: Int
nofBars = 6
bar :: Int -> Bar
bar 1 = [Up, Down, Hole]
bar 2 = [Up, Down, Hole]
bar 3 = [Up, Hole, Down]
bar 4 = [Up, Hole, Hole]
bar 5 = [Up, Down, Down]
bar 6 = [Up, Down, Up ]
bar _ = []
Определять функции, подобные функции bar, хорошо. Такие функции позволяют использовать конструкции типа map bar [1..nofBars] для получения списка всех планок. Единственное, что здесь может повлечь логическую ошибку, которая не может быть обнаружена компилятором, так это последний клоз определения функции bar. Ограничивать применение этой функции точным количеством планок в задании придётся вручную, равно как и следить за этим. Ну, конечно, можно покрыть программу модульными тестами, это немного поможет.
Теперь определим две функции, которые по заданной планке возвратят все возможные её повороты в трёхмерном пространстве. Каждая планка может быть использована четырьмя способами — прямо (как нарисовано на диаграмме выше), и повёрнутой по одной из осей. В итоге, получаются такие функции:
variations :: Bar -> [Bar]
variations b = map ($ b) [id,
reverse,
turnover,
reverse . turnover]
turnover :: Bar -> Bar
turnover = map inverse
where
inverse Up = Down
inverse Down = Up
inverse Hole = Hole
Функция turnover поворачивает заданную планку вокруг оси X (направленной горизонтально слева направо). Обращение списка просто поворачивает планку вокруг вертикальной оси Y. А вот одновременное обращение и переворот задают вращение вокруг оси Z, которая направлена от читателя в экран.
Наконец, нам потребуется функция, которая по заданной планке даёт для неё некорый идентификатор, по которому можно понять, как расположена планка. Вот её определение:
barID :: Bar -> String
barID b = if null candidates
then "??"
else snd $ head candidates
where
candidates = filter ((b', s) -> b' == b) $
concatMap ((b', s) -> zip (variations b') $ map (s ++) ["N", "Y", "X", "Z"]) $
map (bar &&& show) [1..nofBars]
Если планка неизвестна этой функции, то она возвращает строку "??". Если же переданная планка находится среди изначальных шести (в том числе и среди всех поворотов), то возвращается номер планки и ось, вокруг которой она повёрнута. Символ N добавляется к номеру для неповёрнутой планки. Тут единственная незадача — из-за того, что первая и вторая планки в условиях задачи абсолютно одинаковые, данная функция для них вернёт номер 1. Но это не беда, поскольку идентифицировать такую планку можно.
В общем, всё готово для реализации решения. Вот функция:
solver :: [([String], [String])]
solver = nub $
map ((map barID *** map barID) . transposeSecondPlane) $
filter canStack $
map (transposeSecondPlane . splitAt (nofBars `div` 2)) $
concatMap (mapM (variations . bar)) $
permutations [1..nofBars]
where
transposeSecondPlane (f, s) = (f, transpose s)
Рассмотрим её подробно. Локальная функция transposeSecondPlane транспонирует второй уровень. Здесь мы пользуемся тем, что уровень определён в виде матрицы, то есть списка списков, а для транспонирования матрицы в таком представлении есть стандартная функция transpose из модуля Data.List. Запомним — эта локальная функция потребуется пару раз.
Ну и теперь алгоритм решения. Для начала строится список всех возможных комбинаций чисел от 1 до nofBars (которое равно 6 в этой задаче). Далее к каждой такой комбинации применяется сложная функция mapM (variations . bar). Эта функция сначала применяет к числу функци bar и получает описание планки. Затем для каждой планки получается список её возможных ориентаций в трёхмерном пространстве (функция variations). Далее при помощи монадической функции mapM для списка возвращается список комбинаций элементов, каждый из которых берётся из списков вариантов ориентаций. Чтобы понять, что делает эта функция, можно рассмотреть один пример. Допустим, есть комбинация [1, 2, 3, 4, 5, 6]. Для этой комбинации функция mapM вернёт что-то вроде [["1N", "2N", "3N", "4N", "5N", "6N"], ["1N", "2N", "3N", "4N", "5N", "6Y"], [...], ...], и именно этот список будет состоять из трёх миллионов комбинаций. Комбинаторный взрыв в самом его непосредственном проявлении. (Впрочем, здесь надо отметить, что тут приведены идентификаторы планок, в то время как на деле в памяти будут храниться сами планки). Применение функции concatMap снимает один уровень списка, поскольку в приведённом примере все элементы сгруппированы по 4 (по количеству вариантов ориентации планки).
Далее мы к каждому элементу, состоящему из 6 возможных вариантов планок применяем такую конструкцию. Список из 6 элементов разделяется на пару из двух списков по 3 элемента в каждом. Ко второму элементу применяется транспонирование. И так опять же ко всем трём миллионам вариантов. После этого фильтруем полученный список из трёх миллионов элементов при помощи функции canStack. Она просто проверяет для всех ячеек матрицы возможность их сопряжения. Определение довольно-таки банально:
canStack :: (Plane, Plane) -> Bool
canStack = uncurry ((and .) . zipWith ((and .) . zipWith canStack'))
where
canStack' Up Up = False
canStack' Up Down = False
canStack' Up Hole = True
canStack' Down Up = True
canStack' Down Down = False
canStack' Down Hole = True
canStack' Hole Up = True
canStack' Hole Down = True
canStack' Hole Hole = True
Вся вот эта магия с (and .) . zipWith требуется для разворачивания двух уровней списков и подучения доступа к ячейкам на каждой планке. Ну а функция uncurry требуется потому, что аргументы приходят в эту функцию в паре, а не каррированным способом.
Возвращаемся к рассмотрению функции solver. Далее, после фильтрации, производится обратное транспонирование второго уровня, а за ним — получение идентификаторов всех планок для более хорошего представления решений для пользователя. Впрочем, такое представление тоже несколько негодное, но пока простим. Ну и, наконец, при помощи функции nub осуществляется выкидывание из результирующего списка всех повторных решений. Вот, собственно, и всё.
Осталось только подключить пару модулей и импортировать из них требуемые функции:
import Control.Arrow ((&&&), (***))
import Data.List (nub, permutations, transpose)
На этом точно всё.
Заключение
Описанный в данной заметке модуль можно получить здесь: BallsAndHoles.hs. Если запустить функцию solver, то на консоль будет выведен следующий список решений (здесь он для пущего удобства структурирован):
[(["5N","1X","4Z"], ["1Z","3N","6N"]),
(["4Z","1X","5N"], ["1X","3Y","6N"]),
(["5Y","1Z","4X"], ["6N","3N","1Z"]),
(["1Y","6X","4X"], ["5X","3N","1Z"]),
(["4X","6X","1Y"], ["5Z","3Y","1X"]),
(["4X","1Z","5Y"], ["6N","3Y","1X"]),
(["5Y","3N","1N"], ["4N","6N","1Z"]),
(["1N","3N","5Y"], ["4Y","6N","1X"]),
(["1N","3N","6X"], ["4Y","1N","5X"]),
(["6X","3N","1N"], ["4N","1Y","5Z"]),
(["1N","6X","4Z"], ["1Z","3N","5X"]),
(["4Z","6X","1N"], ["1X","3Y","5Z"]),
(["1Y","3Y","6X"], ["5X","1N","4Y"]),
(["1Y","3Y","5N"], ["1X","6N","4Y"]),
(["5N","3Y","1Y"], ["1Z","6N","4N"]),
(["6X","3Y","1Y"], ["5Z","1Y","4N"])]
Эти решения даны вразнобой и соответствуют двум следующим:
|
|
Осталось перечислить некоторые недочёты, исправление которых остаётся на усмотрение читателя :). Вот они:
- Желательно, конечно, сделать автоматическое удаление из списка решений всех повторов, связанных с поворотами и отражениями. Это можно сделать при помощи сравнения, какие планки используются для формирования плоскостей, без учёта их ориентации в пространстве и расположения в верхней или нижней плоскости.
- Сделать более человеческий вывод о том, как должны быть расположены планки для решения. Для этого можно, например, перекодировать строки типа
"1Y","5N"и т. д. в человеческое описание на естественном языке.
Всем прочитавшим статью — уважение и благодарность.
Мои предыдущие статьи о конкурсах по ФП на Хаброхабре:
- Решение задачи о перегорающих лампочках на языке Haskell
- Фреймворк для решения задач о переправах на языке Haskell
- Конструирование и вычисление арифметических выражений на языке Haskell
- Расшифровка кода на языке Haskell (конкурс по ФП в январе 2012)
- Шахматные задачи на мат в один ход: решение на языке Haskell
- Измерение объёмов при помощи двух заданных сосудов: решение на языке Haskell
- Трансмутации слов друг в друга: решение на языке Haskell
- Решение арифметических задач — вероятностный подход против регулярных выражений
- Поиск кратчайшего расстояния между точками в трёхмерном пространстве
- Управление лифтами: решение на языке Haskell
- Решение логических задач на языке Haskell: в своём ли уме Валет?
- Поиск скрывающегося Доктора X среди пациентов — решение более сложных логических задач
Автор: Darkus
