Как-то давно хотелось чего-то написать, но всё уж было. А тут представился случай, да тем более интернет сразу ничего не выдал…
Я хотел бы сказать большое спасибо А. Дайняк за прочитанный курс и добавить, что это лишь изложение кусочка курса, и на большее я не претендую.
Всюду в статье дерево = бинарное дерево
Действительно нетрудно отрисовывать маленькие деревья (напр. 5-10) листов. И для них можно использовать естественное представление (которое типа ЛКП). И это получается довольно неплохо.
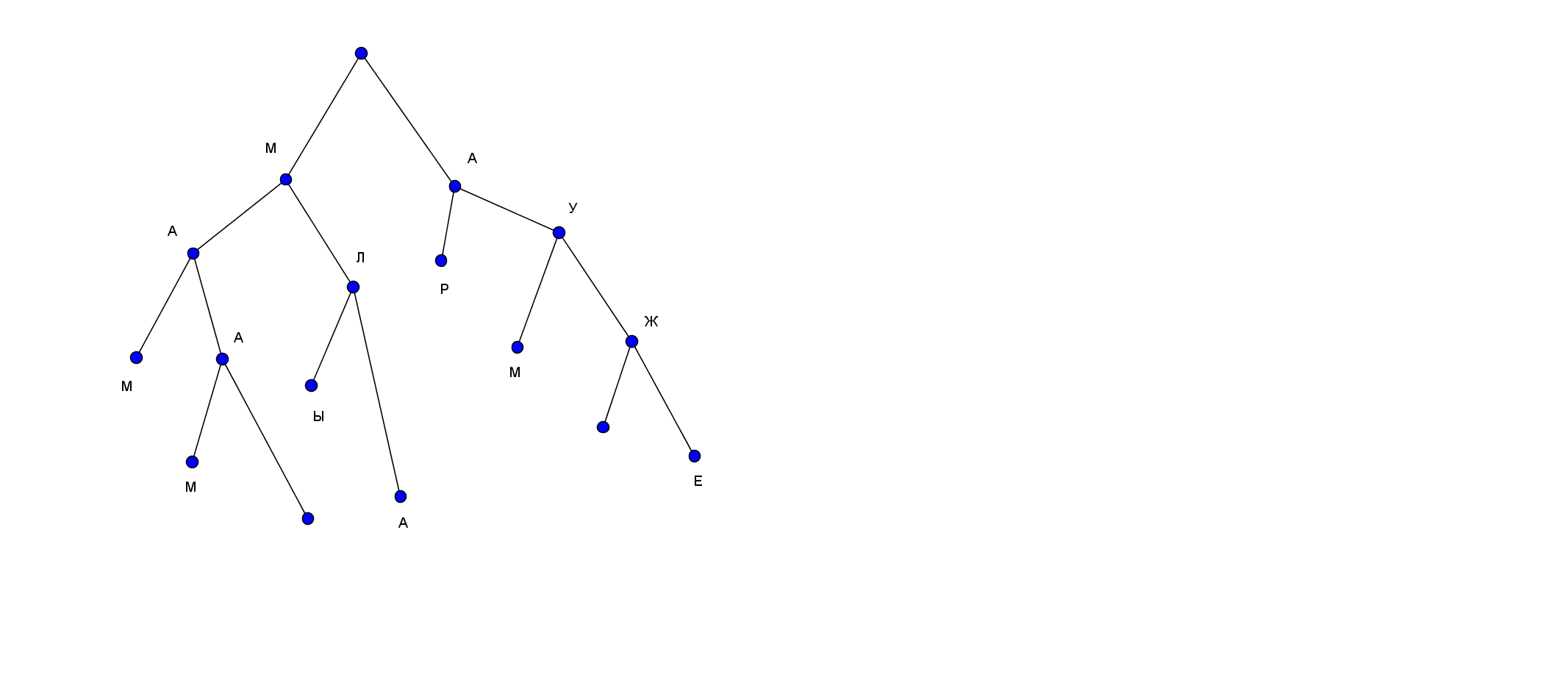
Может быть даже можно попробовать нарисовать дерево из 100 узлов. Но вот если узлов больше — например 1000, то можно рисовать деревья. Но вот читать их (и понимать) будет совсем неудобно. Причём под чтением мы понимаем именно изображение дерева на экране, такое чтобы их просто не замазало бесконечно сильно, т.е. в одно большое пятно.
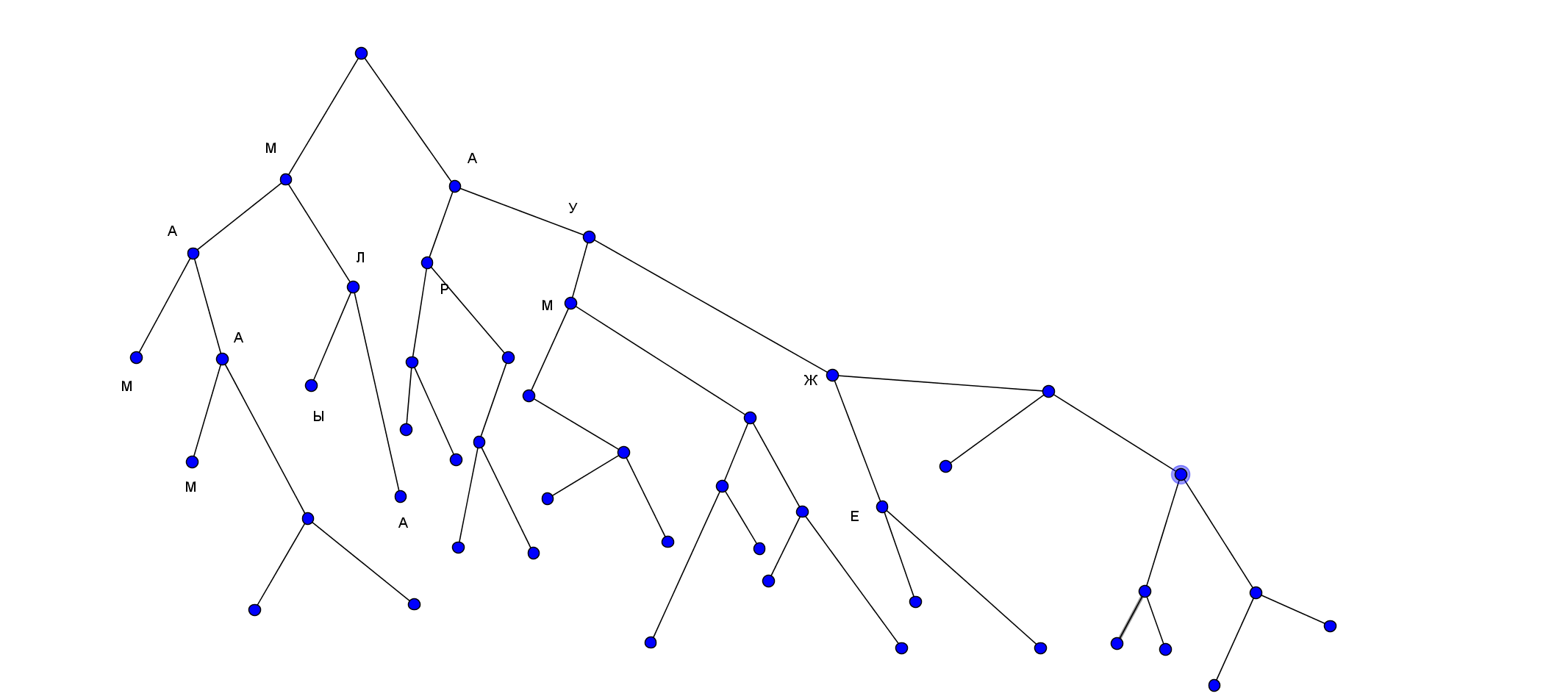
Одним из вариантов борьбы с этим, но наверно даже не сколько борьбы, а просто какой-то структуры нормальной визуализации — Horisontal Vertical-дерево. То есть для визуализации используется вот что:
- Мы гуляем только в
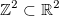. Хотя это совершенно необязательно с точки зрения реализации. Просто так будет удобно нам. - Нам бы хотелось чтобы мы как-то удачно выигрывали в площади и читаемости. (Но рассказывать об этом сейчас не хочется, может быть только сказать, что суперузкая и длинная полоска-дерево совсем не читается.)
Так вот — концепция представления HV-tree проста (и рекурсивна): если у нас есть дерево 1 и дерево 2 и мы хотим объединить их (т.е. сделать поддеревьями одного и того же дерева, то вот как будет делаться такая операция:
То есть как происходит склейка совершенно формально:
1. У нас есть заданная длина ребра (что в общем-то естественно). И склеивать мы можем во по какому правилу. Что мы делаем:
Встаём в корень, S=0. Идём из корня до всех листов и каждый раз как идём вправо (от экрана) S=S+1.
2. То же самое со вторым деревом.
3. Вниз мы закрепляем дерево, которое шире (у которого S больше). А вправо — оставшееся.
Если они равны — нам не принципиально как вешать (хотя конечно нам бы лучше длинное вниз, если мы всё-таки хотим как-то ограничивать рисунок, но если мы не ограничены в представлении — стоит попробовать сделать наоборот — видеть будет удобнее).
Вот именно так мы определяем такие деревья и процесс и построения.
Ну и в качестве примера — сравнение представления в стд виде и HW-укладке.
- Неполное дерево в стд. представлении.
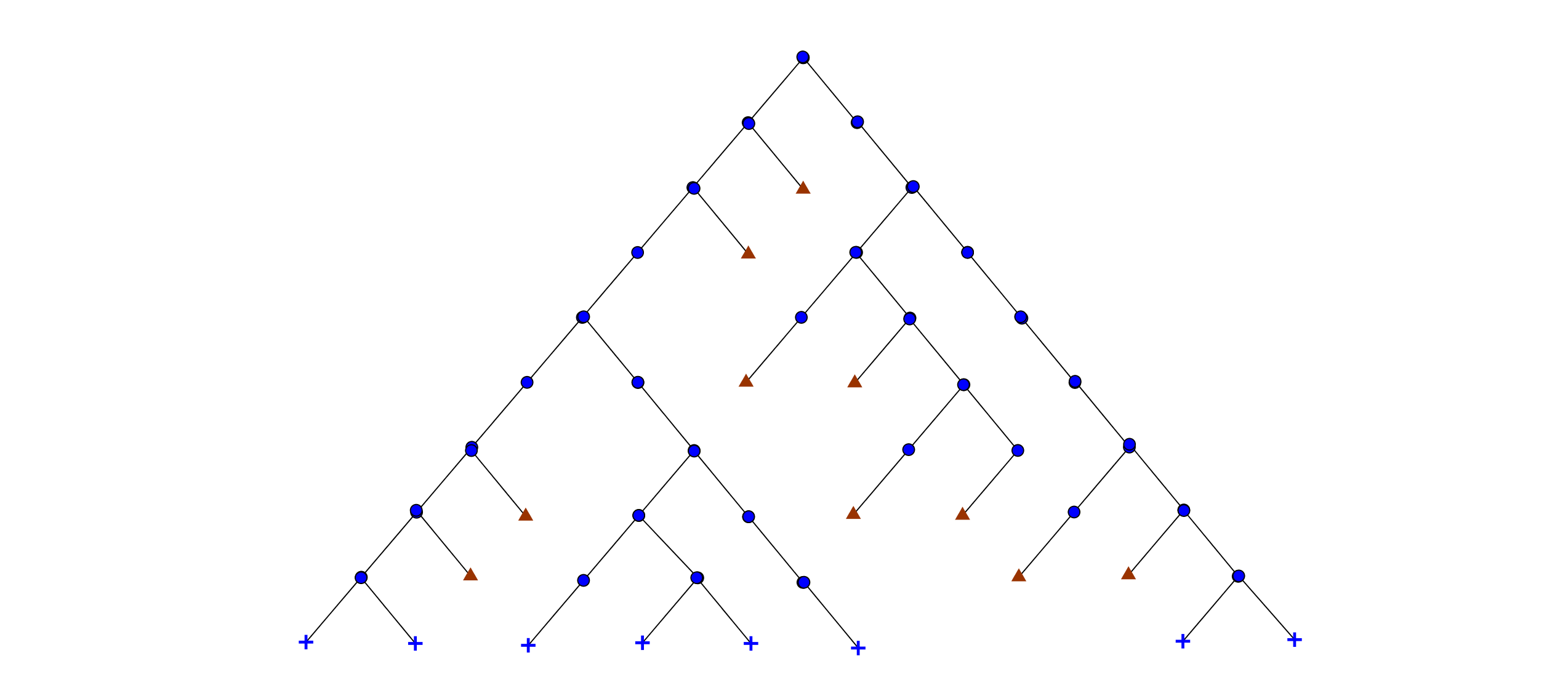
- Полное дерево в стд. представлении: Надо сказать, что мы не сумеем представить всё дерево рёбрами одной ширины. (А точнее — если ребро идёт из узла на n снизу уровне (лист — уровень 0, предлист — 1), то длина ребра должна бы быть n*s, где s-- единичное ребро. (В моём рисунке не сразу так, потому что я подвигал углы рёбер.)
- Первое дерево в HV-представлении. Это то же дерево, что и на первой картинке.
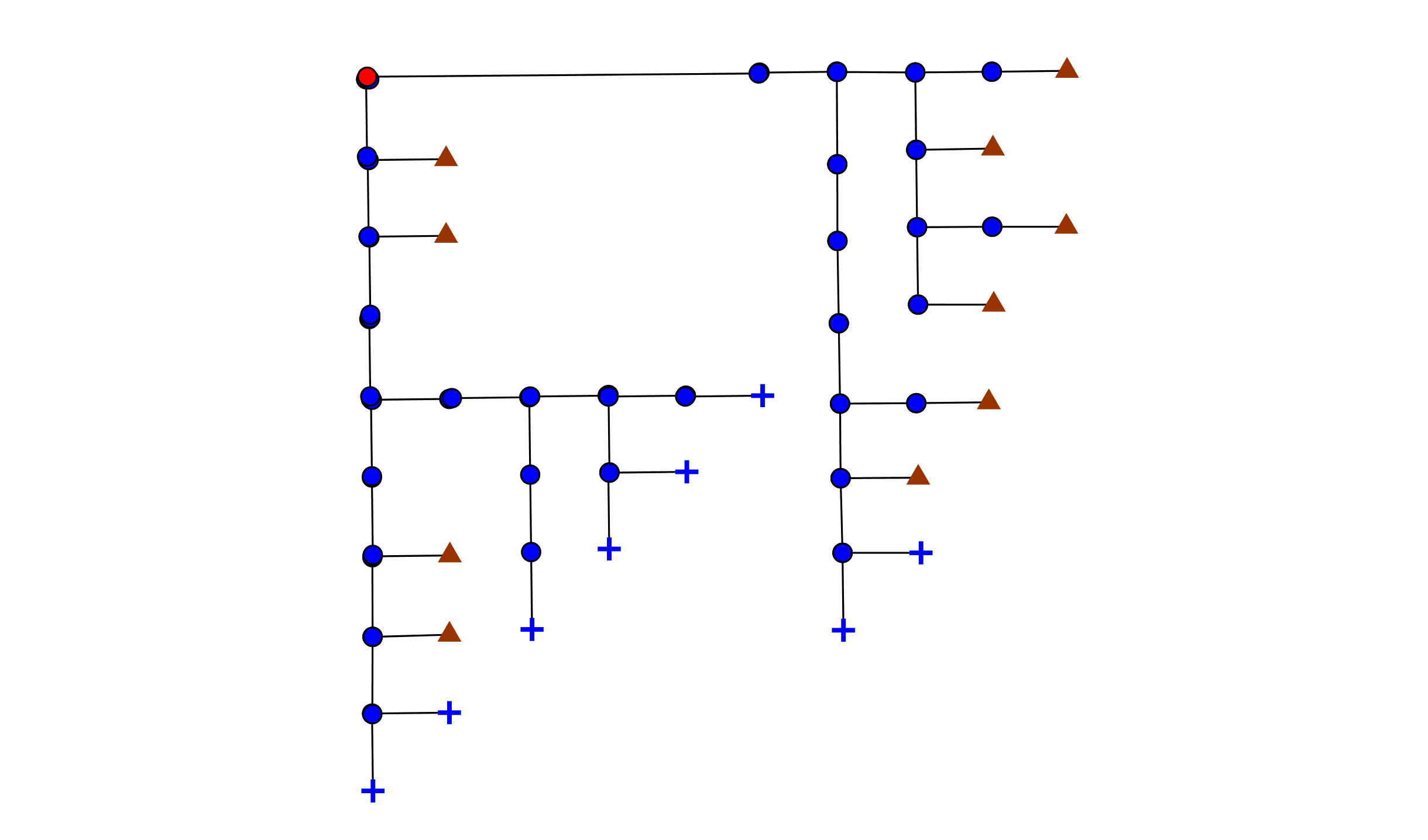
Вот. Такое вот представление, которое в принцип читается несколько лучше, чем стандартное представление.
Автор: Zhe_Ver
