Аннотация
В данной статье хочу рассказать как можно эффективно распараллелить алгоритм BFS — поиск в ширину в графе с использованием графических ускорителей. В статье будет приведен подробный анализ полученного алгоритма. Вычисления выполнялись на одном GPU GTX Titan архитектуры Kepler.
Введение
В последнее время все большую роль играют графические ускорители (GPU) в не графических вычислениях. Потребность их использования обусловлена их относительно высокой производительностью и более низкой стоимостью. Как известно, на GPU хорошо решаются задачи на структурных сетках, где параллелизм так или иначе легко выделяется. Но есть задачи, которые требуют больших мощностей и используют неструктурные сетки. Примером такой задачи является Single Shortest Source Path problem (SSSP) – задача поиска кратчайших путей от заданной вершины до всех остальных во взвешенном графе. Решение данной задачи рассмотрено мной в этой статье. Вторым примером задачи на неструктурных сетках является задача Breadth First Search (BFS) — поиска в ширину в неориентированном графе. Данная задача является основной в ряде алгоритмов на графах. Также она немного проще, чем поиск кратчайшего пути. На данный момент алгоритм BFS используется как основной тест для рейтинга Graph500. Далее рассмотрим, как можно использовать идеи решения задачи SSSP в задаче BFS. Про архитектуру GPU компании Nvidia и об упомянутых алгоритмах уже много написано, поэтому в этой статье я не стану дополнительно писать про это. Так же, надеюсь, что понятия warp, cuda блок, SMX, и прочие базовые вещи, связанные с CUDA читателю знакомы.
Формат используемых данных
Так же как и в задаче SSSP будем использовать те же самые преобразования, для того, чтобы увеличить нагрузку на один SMX и снизить количество одинаковых данных, находящихся в глобальной памяти GPU. Основное отличие — для алгоритма BFS не нужны веса в графе. Так же стоит отметить, что нам необходимо хранить не кратчайшие расстояния, а номер уровня, в котором находится данная вершина:
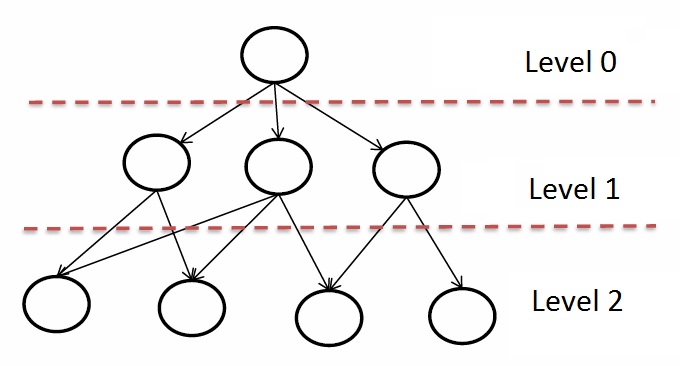
После проведения тестовых запусков выяснилось, что количество уровней в RMAT графах со средней степенью связности 32 не превосходит 10. Поэтому для хранения данных значений будет достаточно unsigned char. Тем самым массив уровней будет занимать в 8 раз меньше места, чем массив расстояний, что очень важно, так как размер кэша в архитектуре Kepler всего 1,5МБ.
Реализация алгоритма на CPU
На CPU был реализован нативный вариант алгоритма обхода в ширину, а именно создание очереди еще не просмотренных вершин. Код CPU реализации выглядит следующим образом:
queue<vertex_id_t> q;
bool *used = new bool[G->n];
for (unsigned i = 0; i < G->n; ++i)
used[i] = false;
used[root] = true;
q.push(root);
dist[root] = 0;
while (!q.empty())
{
vertex_id_t nextV = q.front();
q.pop();
for (unsigned k = G->rowsIndices[nextV]; k < G->rowsIndices[nextV + 1]; ++k)
{
if (used[G->endV[k]] == false)
{
used[G->endV[k]] = true;
q.push(G->endV[k]);
dist[G->endV[k]] = dist[nextV] + 1;
}
}
}
Данный код достаточно прост и, вполне возможно, не оптимален. Он был использован для проверки правильности работы алгоритма на GPU. Цели написать оптимальный алгоритм на CPU не было, поэтому производительность на CPU будет получена данным алгоритмом. Хочу добавить, что на данный момент оптимальных CPU реализаций много и их легко найти. Также предложено множество других подходов и идей реализации алгоритма BFS.
Реализация алгоритма на GPU
За основу реализации был взят все тот же алгоритм Форда-Беллмана и ядро в рассмотренной задаче SSSP. Основное вычислительное ядро для BFS будет выглядеть следующим образом:
if(k < maxV)
{
unsigned en = endV[k];
unsigned st = startV[k];
if(levels[st] == iter)
{
if(levels[en] > iter)
{
levels_NR[en] = iter + 1;
modif[0] = iter;
}
}
else if(levels[en] == iter)
{
if(levels[st] > iter)
{
levels_NR[st] = iter + 1;
modif[0] = iter;
}
}
}
Идея алгоритм в следующем. Пусть массив levels изначально заполнен максимальным для выбранного типа значением (255 для unsigned char). Будем передавать в ядро номер текущей итерации — iter. Далее необходимо просмотреть все ребра и проверить, является ли начальная или конечная вершина текущим родителем, то есть принадлежит ли она уровню iter. Если да, то необходимо пометить противоположную вершину просматриваемой дуги значением на единицу больше, чтобы «включить» эту вершину в список родителей на следующей итерации. Также как и в SSSP, остается переменная modif, показывающая необходимость продолжения разметки графа.
Данный код уже содержит примененные оптимизации в задаче SSSP — использование const __restrict для массива levels и использование другой ссылки levels_NR, указывающей на тот же самый участок памяти, необходимой для записи. Вторая оптимизация в виде перестановки для лучшей локализации данных в кэше тоже была использована. Для алгоритма BFS длина оптимальной кэш линии равна 1024КБ или примерно 1млн элементам массива levels (1024 * 1024) независимо от размера графа.
Анализ полученных результатов
Для тестирования использовались синтетические неориентированные RMAT-графы, которые хорошо моделируют реальные графы из социальных сетей и Интернета. Графы имеют среднюю связность 32, количество вершин является степень двойки. В таблице ниже приведены графы, на которых проводилось тестирование:
| Количество вершин 2^N | Количество вершин | Количество дуг | Размер массива levels в МБ | Размер массива ребер МБ |
| 14 | 16 384 | 524 288 | >0.125 | 2 |
| 15 | 32 768 | 1 048 576 | >0.125 | 4 |
| 16 | 65 536 | 2 097 152 | >0.125 | 8 |
| 17 | 131 072 | 4 194 304 | 0,125 | 16 |
| 18 | 262 144 | 8 388 608 | 0,250 | 32 |
| 19 | 524 288 | 16 777 216 | 0,5 | 64 |
| 20 | 1 048 576 | 33 554 432 | 1 | 128 |
| 21 | 2 097 152 | 67 108 864 | 2 | 256 |
| 22 | 4 194 304 | 134 217 728 | 4 | 512 |
| 23 | 8 388 608 | 268 435 456 | 8 | 1024 |
| 24 | 16 777 216 | 536 870 912 | 16 | 2048 |
Из-за использования самого маленького типа данных для хранения значений уровня, для графа с количеством вершин 220 необходимо 1МБ для кэширования массива levels, в то время как для такого же графа в задаче SSSP необходимо 8МБ. Тестирование производилось на GPU Nividia GTX Titan, у которого 14 SMX и 2688 CUDA-ядер и на процессоре Intel core i7 3го поколения с частотой 3,4ГГц и 8МБ кэша. Для сравнения производительности на CPU использовалась нативная реализация алгоритм поиска в ширь. Никаких оптимизаций в виде перестановки данных перед работой на CPU не производились. Вместо времени показателем производительности будем считать количество дуг, обработанных за секунду времени. В данном случае, необходимо поделить полученное время на количество дуг в графе. В качестве конечного результата бралось среднее значение по 32 точкам. Также вычислялись максимальное и минимальное значения. Для компиляции использовались компиляторы Intel 13й версии и NVCC CUDA 5.5 с флагами –O3 –arch=sm_35.
График средней производительности различных вариантов на GPU и CPU выглядит следующим образом:
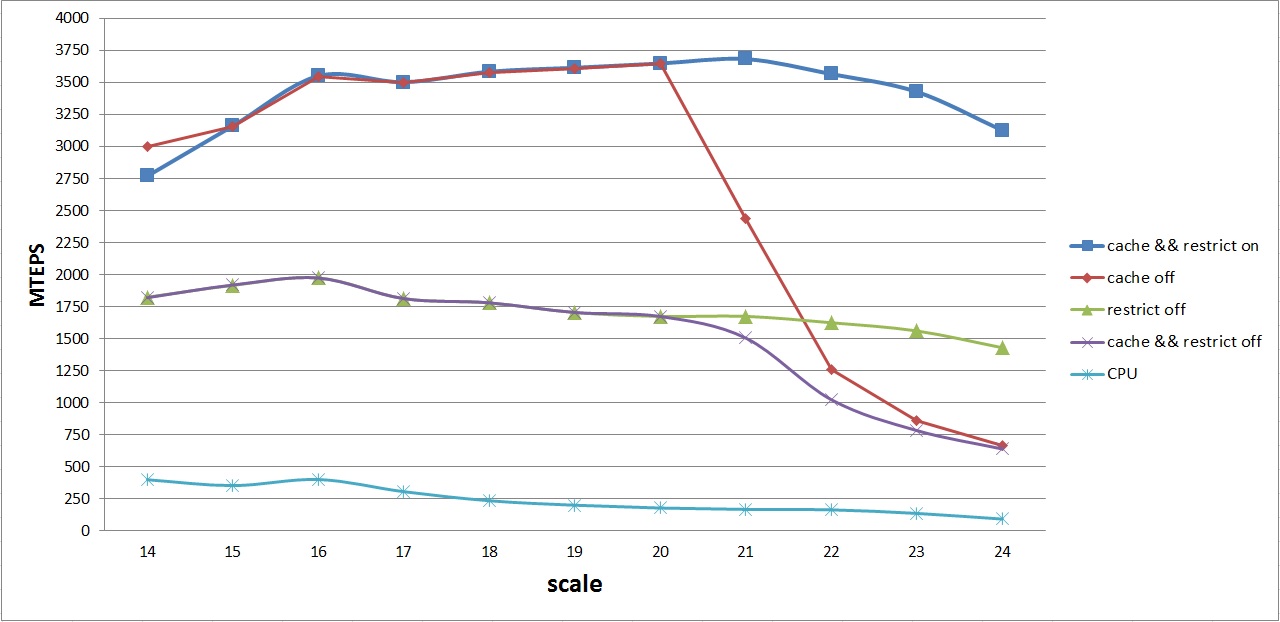
На данном графике изображены кривые средней производительности для следующих алгоритмов:
- cache && restrict on — алгоритм GPU со всеми оптимизациями (1)
- cache off — алгоритм GPU без оптимизации перестановок для улучшенного кэширования (2)
- restrict off — алгоритм GPU без оптимизации текстурного кэша (3)
- cache && restrict off — базовый алгоритм GPU без оптимизаций (4)
- CPU — базовый алгоритм на CPU
Первое, что бросается в глаза — одинаковое поведение алгоритмов (1) — (2) и (3) — (4). Как было отмечено выше, это связано с тем, что массив levels для графов с количеством вершин до 220 помещается в L2 кэш. Поэтому можно не делать перестановку дуг, если рассматривать алгоритмы (1) и (2), и не использовать текстурный кэш в случае (3) и (4).
Далее, можно заметить, что как только массив levels не помещается в L2 кэш, отключение перестановки дает сильный проигрыш в производительности, несмотря на то, что используется const __restrict. Это связано прежде всего со случайным доступом в массив levels. Аналогичная картина наблюдается и в случае отключения опции const __restirict.
Не плавный график в районе степеней 15-16-17 для самого лучшего алгоритма — следствие еще одной маленькой оптимизации — упаковки двух вершин одной дуги в одну переменную типа unsigned int. Так как максимальный номер вершины занимает 16 бит, а unsigned int — 32 бита, то можно упаковать данные о ребре заранее в один unsigned int, а в ядре делать его распаковку, считывая при этом в два раза меньше данных из глобальной памяти GPU.
В итоге, удалось достичь средней производительности в 3,6 GTEPS. Почти пиковая средняя производительность достигается на графах с количеством вершин 216 — 223, что довольно не плохо для данной архитектуры. Максимальная производительность получена на графе с количеством вершин 219 — 4,2 GTEPS.
Полученное ускорение по сравнению с нативной реализацией на CPU оказалось весьма не однозначным:
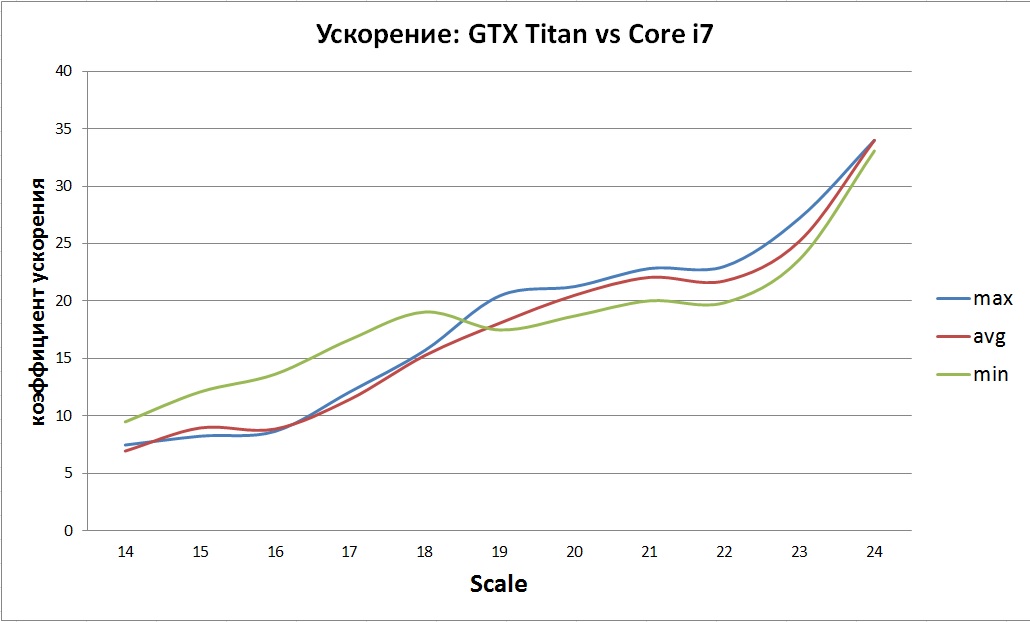
Общая тенденция видна — постепенный рост ускорения. Скорее всего это связано с не эффективной реализаций и ограниченным размером кэша CPU.
Детальный анализ реализованного ядра
В заключение хотел бы показать на сколько эффективен данный подход с точки зрения использования ресурсов GPU. Данный раздел представлен только для интереса и, может быть, для тех, кто в будущем захочет сравнить свой алгоритм с тем, что приведен в данной статье. Рассмотрим детально все то, что выводит профилировщик NVVP для двух графов — 219 и 222. Я выбрал такие графы, потому что у первого массив levels полностью помещается в L2 кэш, а у второго нет. В начале рассмотрим общую информацию:
| Scale | Количество выполненных итераций | Использование разделяемой памяти | Количество используемых регистров | Суммарное время счета ядра в ms | Время копирования массивов в ms |
| 219 | 7 | нет | 12 | 4,512 | 10,97 |
| 222 | 8 | нет | 12 | 41,1 | 86,66 |
Учитывалось копирование массивов вершин на GPU до начала счета и копирование результата на CPU после окончания. Из таблицы видно, что копирование занимает примерно в два раза больше времени, чем весь счет. Далее рассмотрим по итерациям для каждого графа.
Граф 219
| Итерация | Время в ms | GL Eff, % | GS Eff, % | WE Eff, % | NP WE Eff, % | Occupancy, % | L2 Read, GB/s | L2 Write, GB/s | Global Read, GB/s | Global Write, GB/s |
| 1 | 0.577 | 100 | 10 | 100 | 94.6 | 89.3 | 551 | 0.0002 | 110 | 0.0002 |
| 2 | 0.572 | 100 | 8.1 | 99.9 | 94.5 | 89.2 | 551 | 0.0986 | 110 | 0.0498 |
| 3 | 0.58 | 100 | 11,9 | 93.5 | 88.5 | 88.1 | 545 | 14 | 109 | 6 |
| 4 | 1.062 | 100 | 24,3 | 85.1 | 77.7 | 78.2 | 289 | 71 | 58 | 51 |
| 5 | 0.576 | 100 | 9.5 | 91.1 | 86.8 | 88.8 | 549 | 1,37 | 110 | 0.5576 |
| 6 | 0.576 | 100 | 7,8 | 99.6 | 94.2 | 89.2 | 551 | 0.0017 | 110 | 0.0010 |
| 7 | 0.572 | 100 | 0 | 100 | 94.6 | 89.3 | 551 | 0.000 | 110 | 0.000 |
Расшифровка:
- GL Eff — Global Load efficiency
- GS Eff — Global Store efficiency
- WE Eff — Warp Execution efficiency
- NP WE Eff — Non-predicated Warp Execution efficiency
- Occupancy — количество реально активных варпов / максимальное количество варпов на SMX
Из таблицы видно, что наибольшее количество вершин обрабатывается на 3 и 4 итерациях. Из-за этого на 4й итерации виден спад использования пропускной способности L2 и глобальной памяти GPU. Стоит отметить, что по специфике алгоритма на последней итерации не происходит никаких записей. Она необходима для определения завершенности разметки графа. Эффективность исполнения варпов находится в пределах 93-100 % и 85% на самой «загруженной» итерации.
Для сравнения, ниже приведена таблица для графа с 222 вершинами, размер массива levels которого не помещается целиком в L2 кэш GPU.
Граф 222
| Итерация | Время в ms | GL Eff, % | GS Eff, % | WE Eff, % | NP WE Eff, % | Occupancy, % | L2 Read, GB/s | L2 Write, GB/s | Global Read, GB/s | Global Write, GB/s |
| 1 | 4,66 | 100 | 10,4 | 100 | 94.6 | 89.1 | 556 | 0.0001 | 113 | 0.00001 |
| 2 | 4,60 | 100 | 11,8 | 100 | 94.6 | 89.1 | 556 | 0.0014 | 113,2 | 0,0011 |
| 3 | 4,61 | 100 | 11,2 | 99,8 | 94,4 | 89,1 | 555 | 0,5547 | 117 | 0,3750 |
| 4 | 6,405 | 100 | 17,8 | 83.7 | 79.1 | 82.2 | 399 | 46 | 81 | 28 |
| 5 | 7,016 | 100 | 15,8 | 83,6 | 74.1 | 79.8 | 364 | 34 | 74 | 19 |
| 6 | 4,62 | 100 | 7,9 | 90,2 | 85,5 | 89.1 | 555 | 0.0967 | 117 | 0,0469 |
| 7 | 4,60 | 100 | 7,8 | 100 | 94,6 | 89 | 556 | 0.0002 | 113 | 0.0001 |
| 8 | 4,60 | 100 | 0 | 100 | 94.6 | 89.1 | 556 | 0.000 | 113 | 0.000 |
Расшифровка приведена выше. На данном графе наблюдается примерно такая же картина, как и на 219. Пик приходится на 4-5 итерации. По мнению профилировщика NVVP пропускная способность L2 кэша 560 GB/s является высокой (есть низкая, средняя, высокая, максимальная), а глобальной памяти 117 GB/s является средней (есть низкая, средняя, высокая, максимальная).
Заключение
В результате проделанной работы был реализован и оптимизирован алгоритм поиска в ширину на RMAT-графах со средней степенью связности вершин 32. Была достигнута пиковая производительность 4,2 GTEPS и средняя 3,6 GTEPS. Как известно, важна не только производительность, но и энергоэффективность. Наряду с рейтингом Graph500 есть рейтинг Green Graph500, показывающий энергоэффективность. Самое первое место в рейтинге Graph500 по производительности на март 2014 года занимает BlueGene/Q, Power BQC 16C 1.60 GHz с количеством ядер 1048576 и количеством узлов 65536 с производительностью 15363 GTEPS. Потребляемая мощность такой системы составляет 340kW (взято из рейтинга топ 500). Эффективность полученного результата GTEPS/ kW для BlueGene/Q составляет 45. Для реализованного мной алгоритма получается порядка 18 (для расчета бралась общая мощность в 200Вт и средняя производительность 3,6 GTEPS, так как в работе участвует всего одно ядро CPU из 4х и пиковая нагрузка на GPU не достигается).
Еще хотелось бы отметить, что в рейтинге Graph500 есть похожая система Xeon E5-2650 v2, GeForce GTX TITAN, которая на графе 225 получила производительность в 17 GTEPS. К сожалению информации о том, какой был использован граф не приведена. На март 2014 года эта система находится на 58 позиции в рейтинге.
Автор: ALEX_k_s



