Задумывались ли вы, где можно применить навык решения задачек а-ля литкод изи? Я встречаюсь с ними частенько, главное просто присмотреться.
Например, на Linked.in недавно ввели "игры". Я как-то глянул на них на послеобеденном кофе.
"Ферзи" (queens)
Задача проста: расставить ферзей на доске так, чтоб в каждой строке, столбце и связной цветовой области было ровно по одному ферзю, и ферзи не должны касаться друг друга.
Например, ферзи за 28 октября:
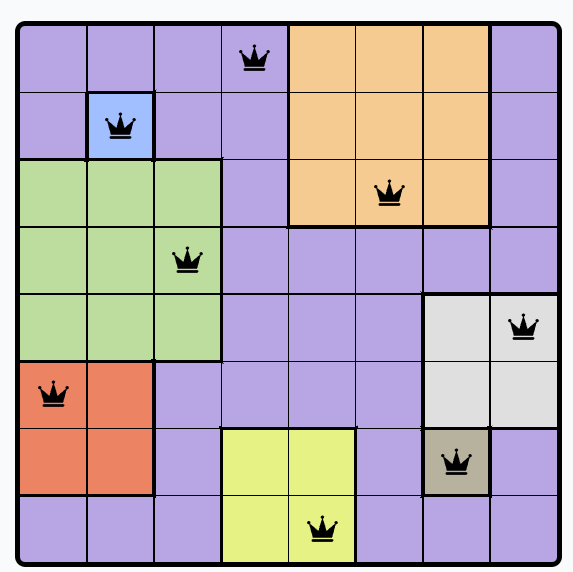
Я решил её раз. Решил другой день. На третий стало понятно, что задачка сама по себе ничего не даёт. Но! Можно развлечься созданием её решателя!
Всё, что нужно, чтобы решать такие задачи -- минимальное знание javascript на уровне синтаксиса, знание, что страница -- это дерево элементов, у которых есть классы, айдишники, и прочие параметры.
И умение формализовать свои мысли: то есть умение решать "литкод изи".
Получение данных
Чтобы решить задачу, надо её сначала получить. Открываем по Ctrl+Shift+J консоль в хроме, наводимся, разворачиваем дерево элементов:
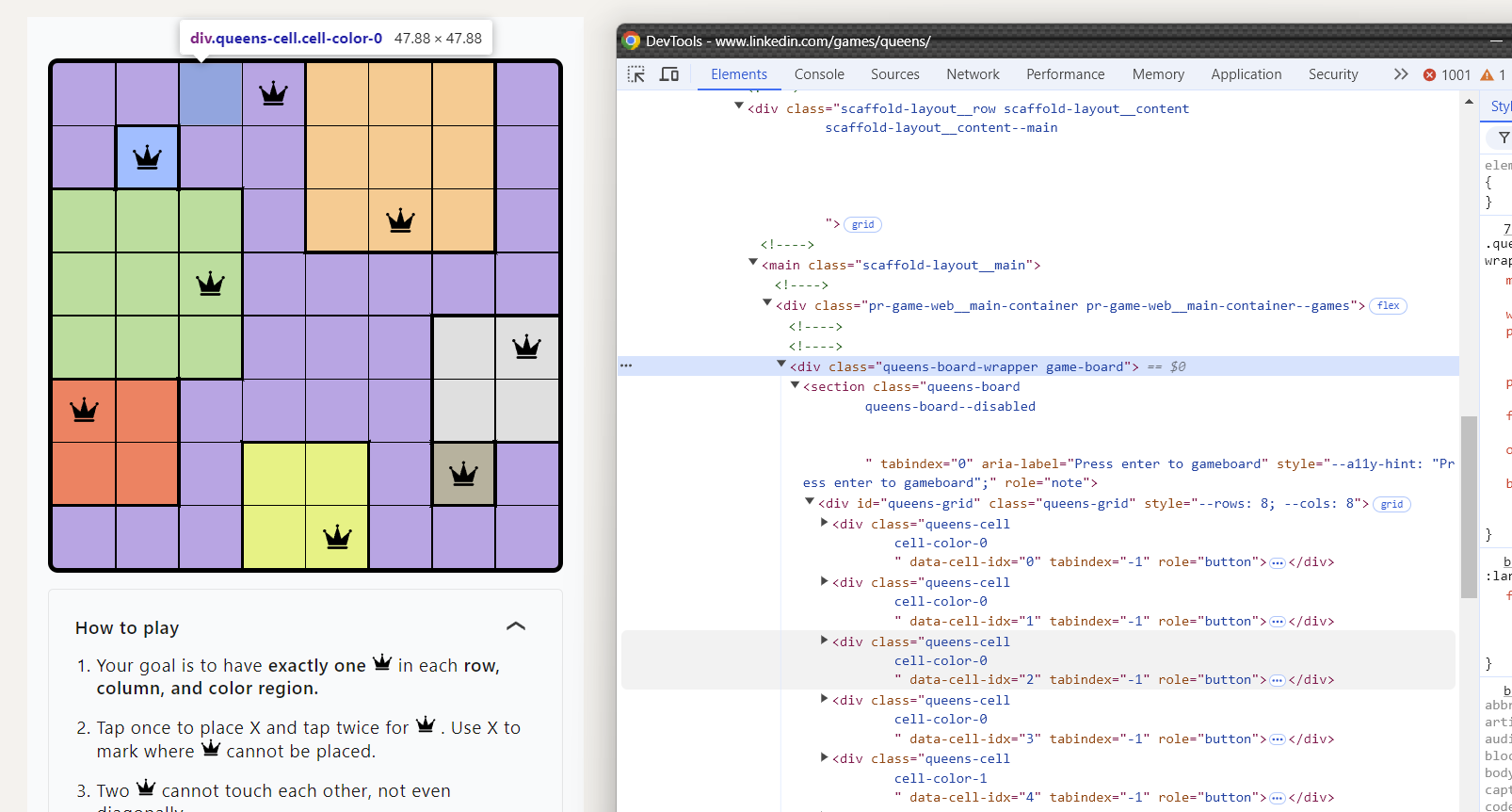
Видим, что ячейки перечислены в форме div элементов с классом queens-cell, и вторым классом cell-color-X, где X -- цвет ячейки. Проверяем, находим их все через document.getElementByClassName('queens-cell'):

Превратим все ячейки в просто номера цветов:
field=Array.from(document.getElementsByClassName('queens-cell')).map((x)=>x.classList[1].split('-')[2]|0);
[0,0,0,0,1,1,1,0
,0,2,0,0,1,1,1,0
,3,3,3,0,1,1,1,0
,3,3,3,0,0,0,0,0
,3,3,3,0,0,0,4,4
,5,5,0,0,0,0,4,4
,5,5,0,6,6,0,7,0
,0,0,0,6,6,0,0,0]Литкодим
Отлично, задача сведена к следующей. Дан одномерный массив размера N^2 элементов, где каждый элемент -- номер цвета. Выдать массив размера N^2 элементов, где 1 стоит в позициях ферзей. В каждой строке, столбце и области цвета должен быть ровно один ферзь. Ферзи не должны касаться друг друга.
Решаем буквально в лоб:
-
Для каждой позиции в первой строке пробуем поставить ферзя.
-
Если ферзя поставили -- переходим к размещению во второй строке.
-
Если не смогли найти решение -- убираем ферзя и переходим к следующей ячейке в строке.
-
Если дошли до конца строки -- возвращаем ошибку.
Получается рекурсивное жадное решение в лоб:
var solve=(r)=>{
for(var c=0;c<N;c++) {
if(ok(r,c)) {
set(r,c,true);
if(r==N-1) return true;
if(solve(r+1)) return true;
set(r,c,false);
}
}
return false;
};
solve(0);Всё, что осталось, это дополнить требуемыми проверками:
-
Вычислим размер поля
var N=Math.sqrt(field.length) -
"В каждой строке": заводим массивчик "в строке есть ферзь":
var rw=Array(N). -
"В каждом столбце":
var cl=Array(N). -
"В каждом цвете":
var cr=Array(N). -
"Не должны касаться": так, тут чуток сложнее, надо проверить, что вокруг заданной точки нет ферзя.
var sol=Array(N*N); // Массив с положением ферзей
var id=(r,c)=>r*N+c; // для удобства, конвертер пары row/col в индекс
var nei=(r,c)=>(r>0&&c>0&&sol[id(r-1,c-1)])||
(r>0&& sol[id(r-1,c)])||
(r>0&& sol[id(r-1,c+1)])||
( c>0&&sol[id(r ,c-1)])||
( sol[id(r ,c)])||
( sol[id(r ,c+1)])||
( c>0&&sol[id(r+1,c-1)])||
( sol[id(r+1,c)])||
( sol[id(r+1,c+1)]);-
Теперь мы можем проверить, можно ли поставить ферзя в клетку r,c, то есть проверки на "нет в ряду, нет в столбце, нет в поле цвета и нет соседа":
var ok=(r,c)=>!rw[r]&&!cl[c]&&!cr[field[id(r,c)]]&&!nei(r,c);-
Функция проставки и убирания ферзя с поля, обновляющая наши массивчики:
var set=(r,c,v)=>{
sol[id(r,c)]=v;
rw[r]=v;
cl[c]=v;
cr[field[id(r,c)]]=v;
};-
Проверяем:

Сложность решения? Для каждой строки до N вариантов, так что O(N^2). Для раз-в-день -- нет смысла даже думать над решением лучше!
Выводим решение
Осталось вывести решение на экран:
fld = Array.from(document.getElementsByClassName("queens-cell"));
for(var i=0;i<fld.length;i++) {
if (sol[i]) { fld[i].style = 'border: 3px solid red'; }
}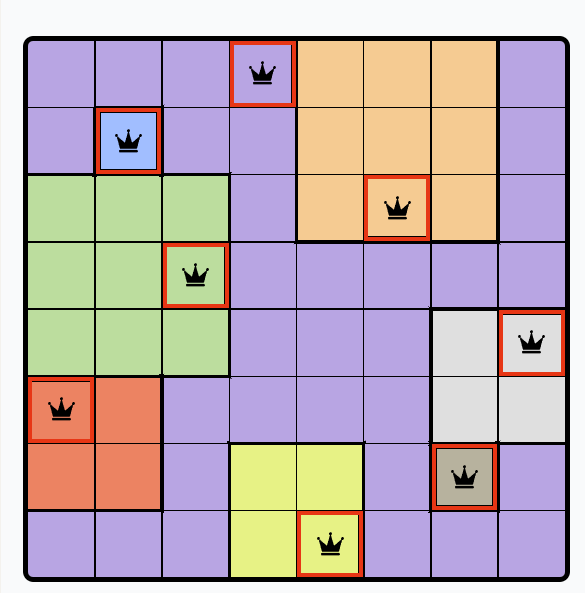
Всё, прокликиваем квадратики и задача решена. Да, можно еще найти кто и как слушает клики, как вызвать их программно (вместо подсветки клетки)... Оставлю это как упражнение для читателя :)
Сливаем всё вместе
Заворачиваем скрипт в готовый для копипасты:
Полный скрипт
((fld)=>{
var field = fld.map((x)=>x.classList[1].split('-')[2]|0);
var N=Math.sqrt(field.length);
var rw=Array(N);
var cl=Array(N);
var cr=Array(N);
var sol=Array(N*N);
var id=(r,c)=>r*N+c;
var nei=(r,c)=>(r>0&&c>0&&sol[id(r-1,c-1)])||
(r>0&& sol[id(r-1,c)])||
(r>0&& sol[id(r-1,c+1)])||
( c>0&&sol[id(r ,c-1)])||
( sol[id(r ,c)])||
( sol[id(r ,c+1)])||
( c>0&&sol[id(r+1,c-1)])||
( sol[id(r+1,c)])||
( sol[id(r+1,c+1)]);
var ok=(r,c)=>!rw[r]&&!cl[c]&&!cr[field[id(r,c)]]&&!nei(r,c);
var set=(r,c,v)=>{
sol[id(r,c)]=v;
rw[r]=v;
cl[c]=v;
cr[field[id(r,c)]]=v;
};
var solve=(r)=>{
for(var c=0;c<N;c++) {
if(ok(r,c)) {
set(r,c,true);
if(r==N-1) return true;
if(solve(r+1)) return true;
set(r,c,false);
}
}
return false;
};
solve(0);
for(var i=0;i<fld.length;i++) {
if (sol[i]) { fld[i].style = 'border: 3px solid red'; }
}
})(Array.from(document.getElementsByClassName("queens-cell")))Для удобства, засунем скрипт в любой минификатор:
Минискрипт
(_=>{var e=_.map(_=>0|_.classList[1].split("-")[2]),r=Math.sqrt(e.length),$=Array(r),s=Array(r),l=Array(r),t=Array(r*r),a=(_,e)=>_*r+e,n=(_,e)=>_>0&&e>0&&t[a(_-1,e-1)]||_>0&&t[a(_-1,e)]||_>0&&t[a(_-1,e+1)]||e>0&&t[a(_,e-1)]||t[a(_,e)]||t[a(_,e+1)]||e>0&&t[a(_+1,e-1)]||t[a(_+1,e)]||t[a(_+1,e+1)],f=(_,r)=>!$[_]&&!s[r]&&!l[e[a(_,r)]]&&!n(_,r),i=(_,r,n)=>{t[a(_,r)]=n,$[_]=n,s[r]=n,l[e[a(_,r)]]=n},o=_=>{for(var e=0;e<r;e++)if(f(_,e)){if(i(_,e,!0),_==r-1||o(_+1))return!0;i(_,e,!1)}return!1};o(0);for(var m=0;m<_.length;m++)t[m]&&(_[m].style="border: 3px solid red")})(Array.from(document.getElementsByClassName("queens-cell")));Теперь откроем вкладку закладок (Ctrl+Shift+B), правой кнопкой => add page => название "Queens Solver", в поле URL пишем javascript: и затем вставляем минимизированный код:
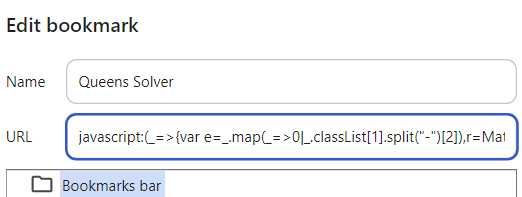
И всё, можем решать в один клик:
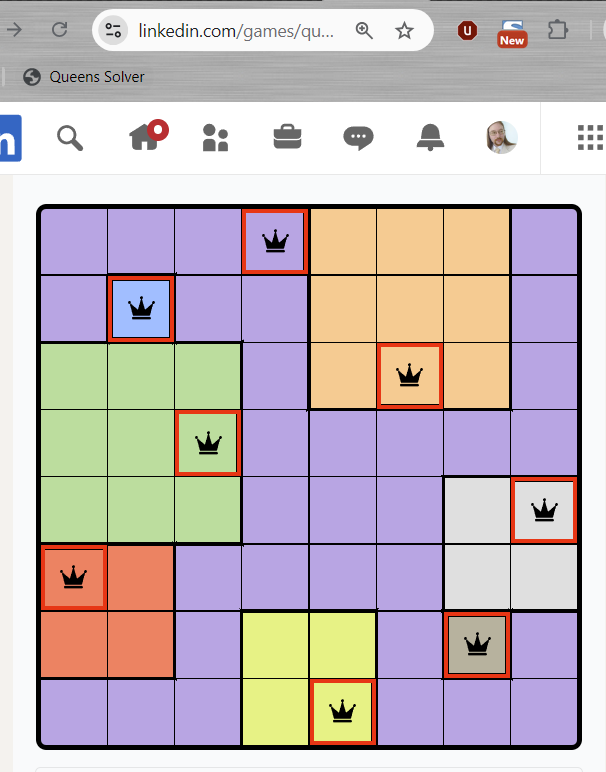
p.s.: Если не смогли сделать решатель для Tango, возьмите тут.
p.p.s.:
Кто заметил, что "в ряду" проверка излишняя? :)
Автор: datacompboy