В октябре 2021 года я опубликовал на Хабре статью «Змей и дротик. От михраба до квазикристаллов», в которой кратко рассказал об апериодических мозаиках, в том числе, составленных Роджером Пенроузом и древнеперсидскими архитекторами. Не припомню, обращался ли я после этого в моём блоге к парадоксальным геометрическим проблемам. Но уже в конце октября текущего 2024 года нашлась ещё одна подобная тема, заслуживающая отдельной статьи на Хабре. Подсказал мне эту историю уважаемый Виктор Георгиевич Сиротин @visirok мой давний собеседник, который создал отличный блог на Хабре и размышляет о программировании и о программной архитектуре как о материализации идей — одноимённую группу он также ведёт в Телеграме. Статья же будет об удивительном сходстве между сегментами раковины наутилуса и очертанием мышечных волокон, которое недавно обнаружили венгерские учёные.
О геометрии без углов
Одна из центральных задач в геометрии — замощение плоскости простыми фигурами. Известны классические замощения плоскости треугольниками, квадратами и шестиугольниками. Ранее я писал на Хабре об игре в танграм, представляющей собой более сложный набор для таких замощений. Аналогичные задачи в пространстве решаются при помощи кубов или других многогранников, и в целом стереометрия трактует фигуры для заполнения пространства как соты. Но такие фигуры обладают ровными прямолинейными рёбрами или гранями, а в природе прямые линии наблюдаются очень редко. Для замощения естественных объёмных фигур потребовались бы криволинейные фигуры с неплоскими гранями и (практически) без выраженных углов. В данном случае привычные многогранники можно расценивать как прототипы или заготовки, которые затем можно постепенно приближать к естественным контурам. Венгерские учёные под руководством Габора Домокоша из Будапештского технологического университета доказали, что существует бесконечное множество пригодных для замощения многоугольников, которые можно плавно деформировать до полного устранения углов — и в таком случае этими фигурами всё равно можно будет выстилать плоскость или другие поверхности. С геометрической точки зрения это будут области Вороного-Дирихле для точечных решёток в двух или трёх измерениях.
Ранее Домокош отметился другими замечательными исследованиями выпуклых фигур. В частности, он описал объект под названием «гёмбец», приближающийся по форме к черепашьему панцирю:

Те фигуры, которые образуются на плоскости при вышеописанном замощении, исследователи назвали «мягкими ячейками». Здесь отметим важное различие между двумя классами замощений. Те многоугольные и многогранные замощения, которые состоят из условных «сот» с плоскими гранями и чётко очерченными углами, находят применение при моделировании в геологии, физике и химии. С их помощью можно описывать сетки трещин, конвективные ячейки, вспенивание, эоловые формы рельефа и супрамолекулярные паттерны. В свою очередь, мягкие ячейки очень хорошо подходят для моделирования поверхностей, которые испытывают биологический рост, у которых постоянно увеличивается кривизна с сохранением самоподобия. В микромире такие паттерны наблюдаются при росте клеток, во флоре – при росте некоторых видов капусты, в фауне особенно типичны для моллюсков, например, для наутилуса:

Другие естественные и искусственные формы, которые можно замостить мягкими ячейками:
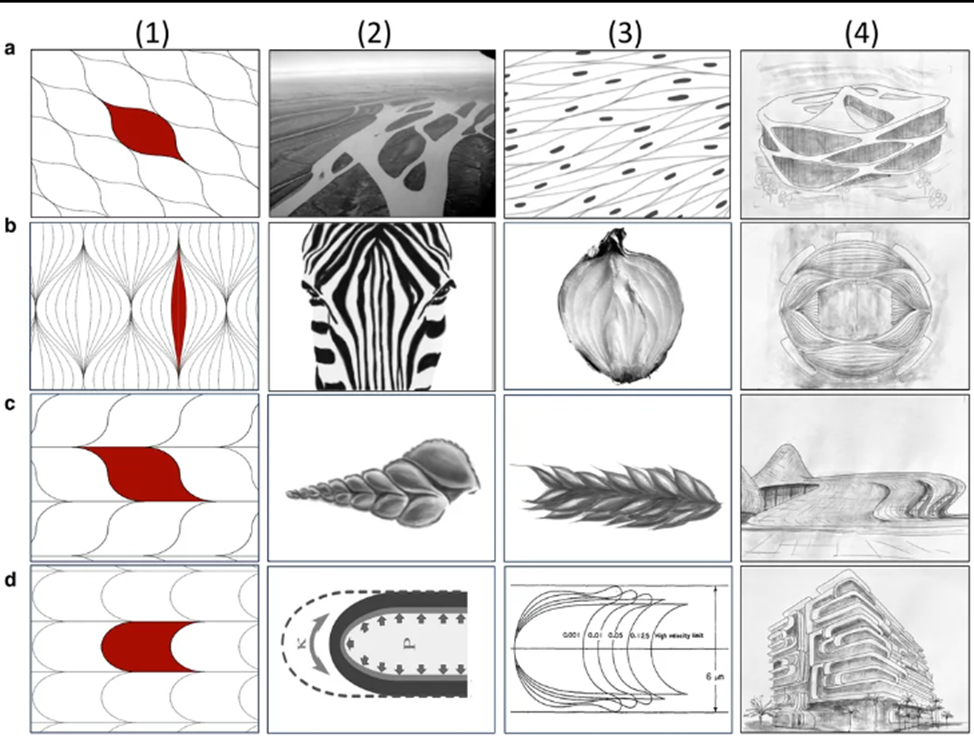
На этой иллюстрации, которую учёные приводят в своей февральской статье, показаны как объекты живой и неживой природы, моделируемые при помощи мягких ячеек, так и эскизы авангардных зданий, проектированием которых занималась Заха Хадид (1950-2016), архитектор иракского происхождения. Вот здание Центра имени Гейдара Алиева, возведённого по её проекту в Баку:

Мягкие ячейки могут фигурировать на 2D- и 3D-поверхностях. В варианте 2D для них характерны криволинейные очертания, в которых иногда встречаются острые углы (очертания островов, полосы на шкуре животных, луковая шелуха).
На 3D-поверхностях вариантов гораздо больше и геометрия усложняется, поскольку мягкие ячейки не образуют вершин. Исследователи из группы Домокоша разработали алгоритм, в котором берётся известный многогранник, все стороны которого являются многоугольниками с прямолинейными сторонами, после чего путём постепенно приближения такие многоугольники преобразуются в ближайшие по форме мягкие ячейки. Стороны многоугольников аккуратно и единообразно деформируются. В процессе такого моделирования было открыто несколько ранее не известных типов мягких ячеек. Процесс такого приближения проиллюстрирован на следующем видео:
На что похожа раковина наутилуса
Особенно интересен этот алгоритм применительно к многокамерной раковине наутилуса. Наутилус может впускать биологические газы в камеры своей раковины и, утяжеляясь таким образом, опускаться на дно. Сам моллюск живёт в передней, самой крупной камере раковины, а остальные камеры использует для впуска и откачивания воды, так, что они образуют гидростатическую систему. Жюль-верновский капитан Немо назвал свой корабль «Наутилусом», поскольку в нём воспроизводилась подобная технология. Уважаемый Максим Агаджанов @marks написал на Хабре статью «Физика в мире животных: наутилус и его осмотический насос», в которой вы можете подробнее познакомиться с этим реликтовым моллюском.
Кристина Регош из группы Домокоша показала, что поперечное сечение любой камеры наутилуса представляет собой плоскую мягкую ячейку с двумя углами, однако в объёмной ячейке вершин нет — это подтверждается на снимках компьютерной томографии. Мягкие ячейки наутилуса и аммонитов заполняют весь объём раковины, нигде не образуя углов.
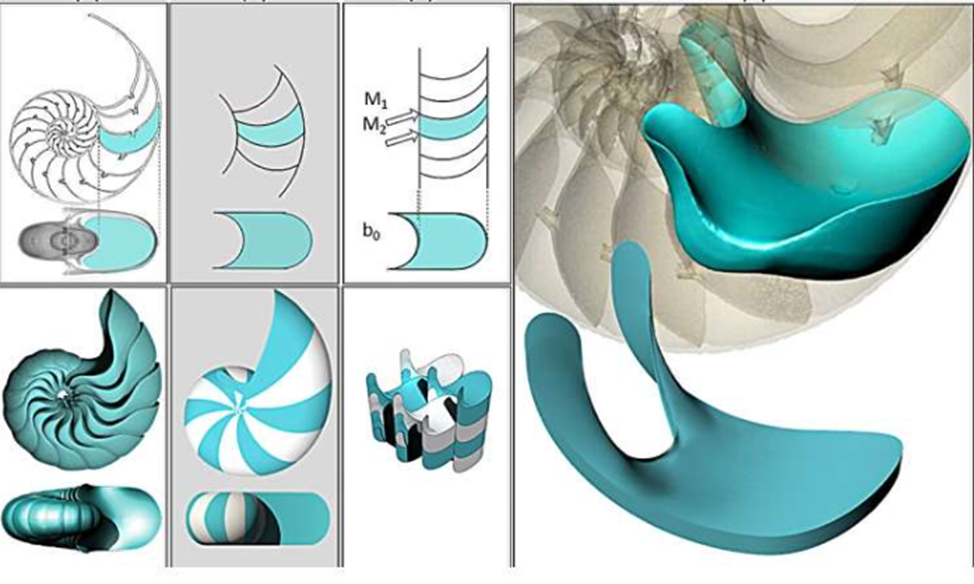
Слева показаны геометрически правильные контуры раковины наутилуса, смоделированные на компьютере, а справа — реальная форма ячейки в сравнении со смоделированной. В природе ячейки в раковине наутилуса имеют более сложную форму, чем показывает алгоритм (отчасти это обусловлено и дарвиновской изменчивостью), но всё равно поддаются описанному замощению.
Мягкие ячейки вполне соотносятся с замощениями из многоугольников путём комбинаторной эквивалентности. Если представить замощённую поверхность как гибкий и пластичный резиновый коврик, то очевидно, что он не будет рваться под действием различных эластичных деформаций. При этом будет существенно меняться форма и кривизна линий и градусная мера углов, однако с топологической точки зрения поверхность не изменится (смежные области останутся смежными, несмежные — несмежными). В соответствии с геометрией, описанной группой Домокоша, именно комбинаторная эквивалентность позволяет придавать граням выпуклость, а рёбрам — кривизну, не нарушая общей компоновки фигур на плоскости. Здесь мы находим аналогию между образованием живых клеток и образованием пузырьков — в целом неудивительную, поскольку коацерваты, вероятные предшественники клеток, представляли собой стабильные капли биохимического раствора. Обратите внимание, как выглядят образцы застывших пенистых структур:

По-видимому, именно мягкие ячейки являются первокирпичиками биологических форм и показывают, что геометрия живых форм должна принципиально отличаться от геометрии неживых. Концепция мягких ячеек позволяет объяснить не только форму биологических тканей в статике, но и рост, заживление и онтогенез организмов. Например, именно биология мягких ячеек позволяет описать развитие растительных корней или образование биологических фракталов, например, капусты романеско.
В заключение этой статьи напомню ещё об одной моей публикации, «TESSERAE — предыстория орбитального улья». В ней я описал проект постепенно наращиваемой космической станции, модули которой выстраиваются из фигур, подобных по форме додекаэдру или фуллеренам. Обратите внимание, насколько похожи изображения станции из той статьи на структуру многогранников, моделирующих пузырьки пены на иллюстрации выше. Можно предположить, что геометрия, систематизированная группой Домокоша, описывает выращивание не только живых, но и искусственных мягких ячеек. Подобно камерам наутилуса, они могут иметь углы в поперечном сечении, но не иметь их на поверхности. Если алгоритмизировать выращивание мягких ячеек в макро- и миромасштабе, это может решить проблему герметичности в космосе и под водой, а также реализовать новые методы самозалечивания материалов и произвольного изменения формы в зависимости от доступного свободного пространства.
Автор: OlegSivchenko

