Случайное распределение урона в RPG

Для вычисления урона от атаки в таких настольных ролевых играх, как Dungeons & Dragons, используются броски урона. Это логично для игры, чей процесс основан на бросках кубиков. Во многих компьютерных RPG урон и другие атрибуты (сила, очки магии, ловкость и т.д.) вычисляются по похожей системе.

Обычно сначала пишется код вызова random(), а затем результаты корректируются и подстраиваются под нужное игре поведение. В этой статье будут рассмотрены три темы:

1. Простые корректировки — среднее значение и дисперсия
2. Добавление асимметрии — отбрасывание результатов или добавление критических попаданий
3. Полная свобода в настройке случайных чисел, неограниченная возможностями кубиков

Основы

В этой статье предполагается, что у вас есть функция random(N), возвращающая случайное целое число в пределах от 0 до range-1. В Python можно использовать random.randrange(N). В Javascript можно пользоваться Math.floor(N * Math.random()). В стандартной библиотеке C есть rand() % N, но она плохо работает, так что используйте другой генератор случайных чисел. В C++ можно подключить uniform_int_distribution(0,N-1) к объекту генератора случайных чисел. В Java можно создать объект генератора случайных чисел с помощью new Random(), а затем вызывать для него .nextInt(N). В стандартных библиотеках многих языков нет хороших генераторов случайных чисел, но существует множество сторонних библиотек, например, PCG для C и C++.

Давайте начнём с одного кубика. На этой гистограмме показаны результаты бросков одной 12-сторонней кости: 1+random(12). Поскольку random(12) возвращает число от 0 до 11, а нам нужно число от 1 до 12, мы прибавляем к нему 1. На оси X расположен урон, на оси Y — частота получения соответствующего урона. Для одной кости бросок урона 2 или 12 так же вероятен, как и бросок 7.

Для броска нескольких кубиков полезно использовать запись, применяемую в играх с костями: NdS означает, что нужно бросить S-сторонню кость N раз. Бросок одной 12-сторонней кости записывается как sided 1d12; 3d4 означает, что нужно бросить 4-стороннюю кость три раза. В коде это можно записать как 3 + random(4) + random(4) + random(4).

Давайте бросим две 6-сторонние кости (2d6) и суммируем результаты:

damage = 0
for each 0 ≤ i < 2:
    damage += 1+random(6)

Результаты могут находиться в пределах от 2 (на обеих костях выпала 1) до 12 (на обеих костях выпала 6). Вероятность получения 7 выше, чем 12.

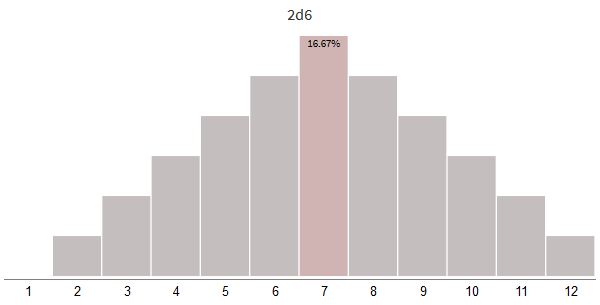
Что произойдёт, если мы увеличим количество костей, но уменьшим их размер?

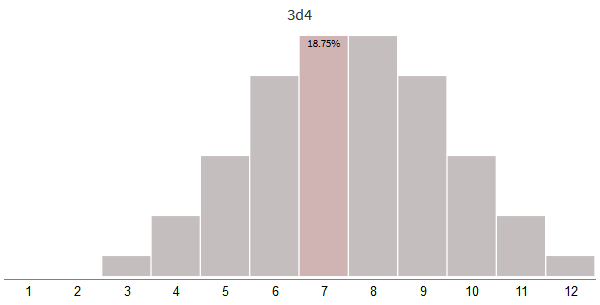
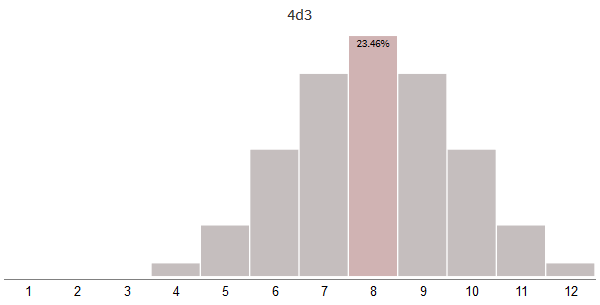
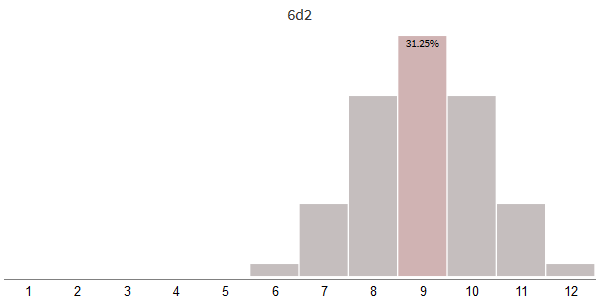
Самый важный эффект — распределение станет не широким, а узким. Есть и второй эффект — пик смещается вправо. Давайте для начала исследуем использование смещений.

Постоянные смещения

Часть оружия в Dungeons & Dragons даёт бонусный урон. Можно записать 2d6+1, чтобы обозначить бонус +1 к урону. В некоторых играх броня или щиты снижают урон. Можно записать 2d6-3, что обозначает снятие 3 очков урона (в этом примере я предположу, что минимальный урон равен 0).

Попробуем смещать урон в отрицательную (для снижения урона) или в положительную (для бонуса урона) стороны:

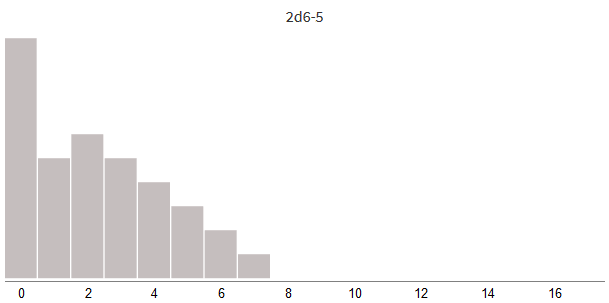
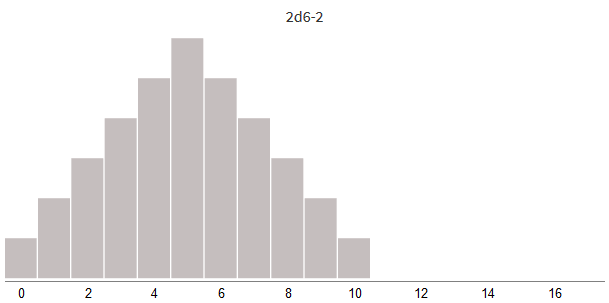
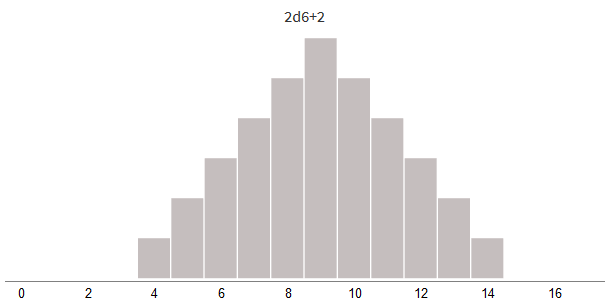
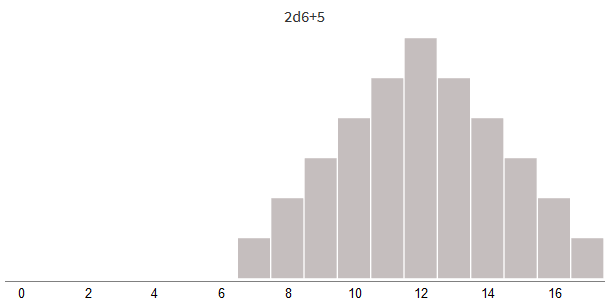
Прибавляя бонус урона или вычитая заблокированный урон, мы просто смещаем всё распределение влево или вправо.

Дисперсия распределения

При переходе от 2d6 к 6d2 распределение становится уже и смещается вправо. Как мы видели в предыдущем разделе, смещение — это простой сдвиг. Давайте рассмотрим дисперсию распределения.

Определим функцию для N бросков подряд random(S+1), возвращающую число от 0 до N*S:

function rollDice(N, S):
    # Сумма N костей, каждая из которых имеет значение от 0 до S
    value = 0
    for 0 ≤ i < N:
        value += random(S+1)
    return value

Генерирование случайных чисел от 0 до 24 с помощью нескольких костей даёт следующее распределение результатов:

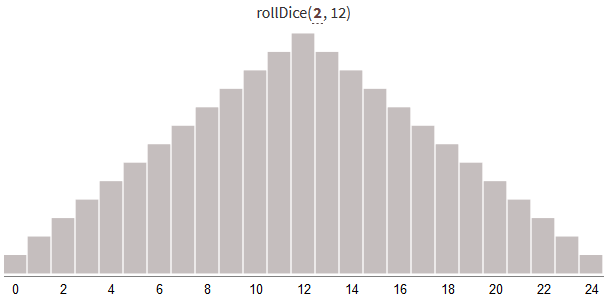
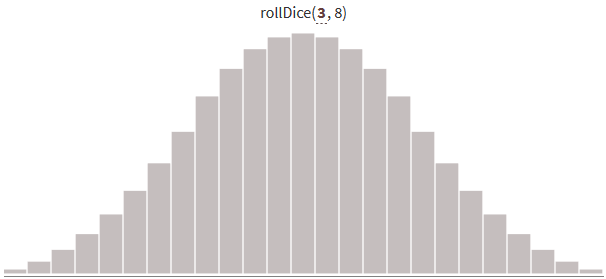
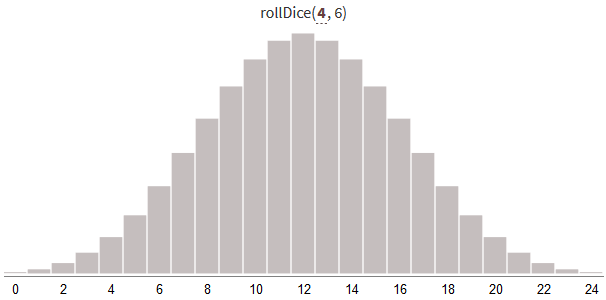
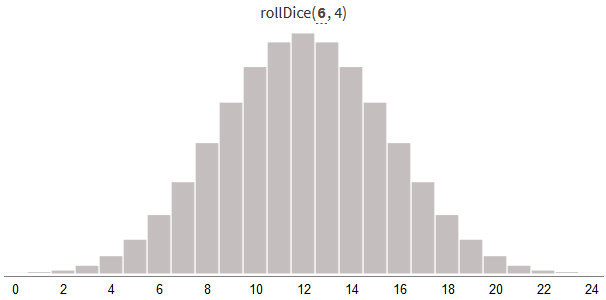
При увеличении количества бросков и сохранении постоянного диапазона от 0 до N*S распределение становится уже (с меньшей дисперсией). Больше результатов будет рядом с серединой диапазона.

Примечание: при увеличении количества сторон S (см. изображения ниже) и делении результата на S распределение приближается к нормальному. Простой способ случайного выбора из нормального распределения — преобразование Бокса-Мюллера.

Асимметрия

Распределения для rollDice(N, S) симметричны. Значения меньше среднего так же вероятны, как и значения выше среднего. Подойдёт ли это для вашей игры? Если нет, то существуют разные техники создания асимметрии.

Отсечение бросков или перебрасывание

Предположим, нам нужно, чтобы значения больше среднего были более частыми, чем меньше среднего. Такая схема редко используется для урона, но применима для таких атрибутов, как сила, интеллект и т.д. Один из способов её реализации — сделать несколько бросков и выбрать лучший результат.

Давайте попробуем бросить кубики rollDice(2,20) дважды и выберем максимальный результат:

roll1 = rollDice(2, 20)
roll2 = rollDice(2, 20)
damage = max(roll1, roll2)

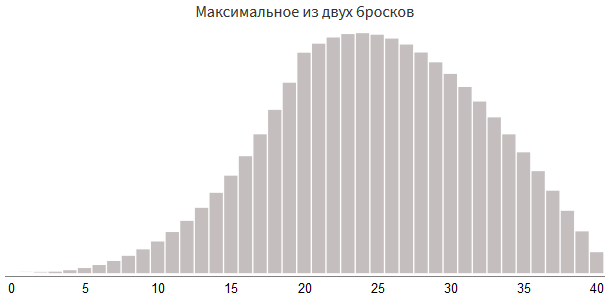
При выборе максимального из rollDice(2, 12) и rollDice(2, 12) у нас получится число от 0 до 24. Ещё один способ получения числа от 0 до 24 — использовать rollDice(1, 12) трижды и выбрать лучшие два из трёх результатов. Форма будет ещё более ассиметричной, чем при выборе одного из двух rollDice(2, 12):

roll1 = rollDice(1, 12)
roll2 = rollDice(1, 12)
roll3 = rollDice(1, 12)
damage = roll1 + roll2 + roll3
# теперь отбрасываем наименьшее:
damage = damage - min(roll1, roll2, roll3)

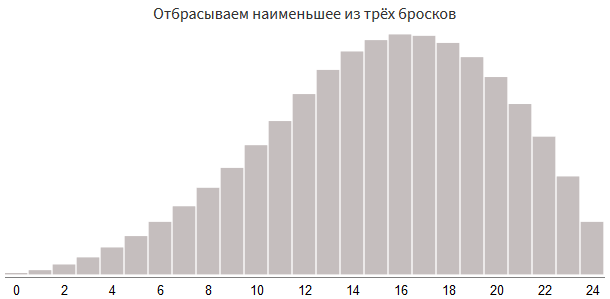
Ещё один способ — перебрасывать наименьший результат. В целом он похож на предыдущие подходы, но немного отличается в реализации:

roll1 = rollDice(1, 8)
roll2 = rollDice(1, 8)
roll3 = rollDice(1, 8)

damage = roll1 + roll2 + roll3
# теперь отбрасываем наименьшее и бросаем снова:
damage = damage - min(roll1, roll2, roll3)
                + rollDice(1, 8)

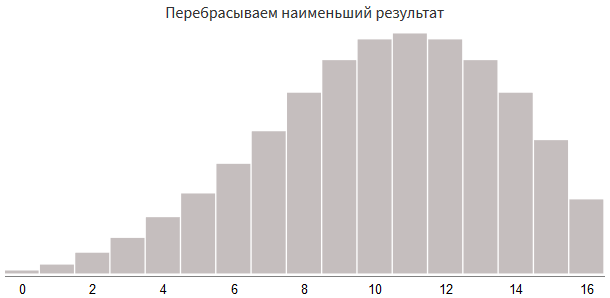
Любой из этих подходов можно использовать для обратной асимметрии, сделав более частыми значения меньше среднего. Можно также считать, что распределение создаёт случайные всплески высоких значений. Такое распределение часто используется для урона и редко — для атрибутов. Здесь max() мы меняем на min():

roll1 = rollDice(2, 12)
roll2 = rollDice(2, 12)
damage = min(roll1, roll2)

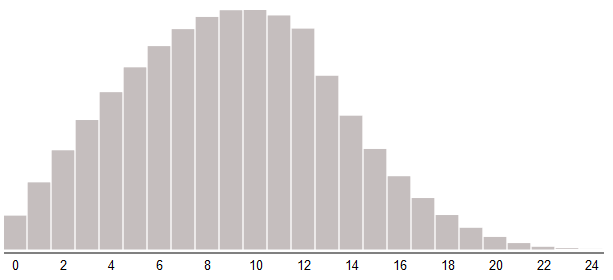
Отбрасываем наибольшее из двух бросков

Критические удары

Ещё один способ создания случайных всплесков высокого урона — их более непосредственная реализация. В некоторых играх определённый бонус даёт «критический удар». Простейший бонус — это дополнительный урон. В представленном ниже коде урон от критического удара прибавляется в 5% случаев:

damage = rollDice(3, 4)
if random(100) < 5:
    damage += rollDice(3, 4)

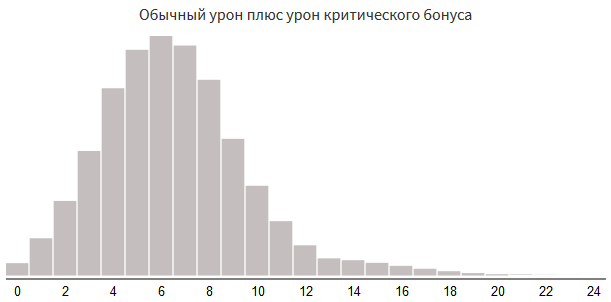
Вероятность критического урона 5%

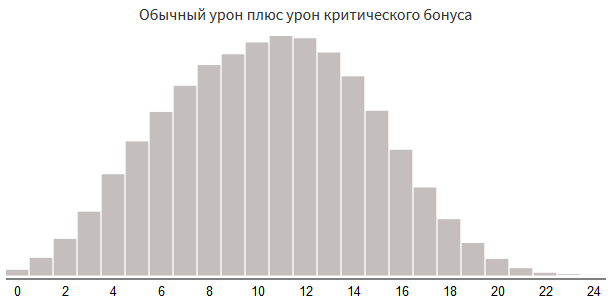
Вероятность критического урона 60%

В других подходах к добавлению асимметрии используются дополнительные атаки: при критических ударах есть шанс на срабатывание дополнительных критических ударов; при критических ударах срабатывает вторая атака, пробивающая защиту; при критических ударах противник промахивается при атаке. Но в этой статье я не буду рассматривать распределение урона при множественных атаках.

Попробуем создать собственное распределение

При использовании случайности (урон, атрибуты и т.д.) надо начинать с описания характеристик распределения, которое нам требуется для игрового процесса:

• Интервал: какими будут минимальное и максимальное значения (если они есть)? Используйте масштабирование и смещение, чтобы уместить распределение в этом интервале.
• Дисперсия: насколько часто значения должны быть близки к среднему? Можно использовать меньшее количество бросков для большей дисперсии или большее количество для меньшей дисперсии.
• Асимметрия: нужно ли, чтобы чаще встречались значения больше или меньше среднего? Используйте min, max или критические бонусы для добавления в распределение асимметрии.

Вот пара примеров с некоторыми из параметров:

value = 0 + rollDice(3, 8)
# Min с перебрасыванием:
value = min(value, 0 + rollDice(3, 8))
# Max с перебрасыванием:
value = max(value, 0 + rollDice(3, 8))
# Критический бонус:
if random(100) < 15:
    value += 0 + rollDice(7, 4)

value = 0 + rollDice(3, 8)
# Min с перебрасыванием:
value = min(value, 0 + rollDice(3, 8))

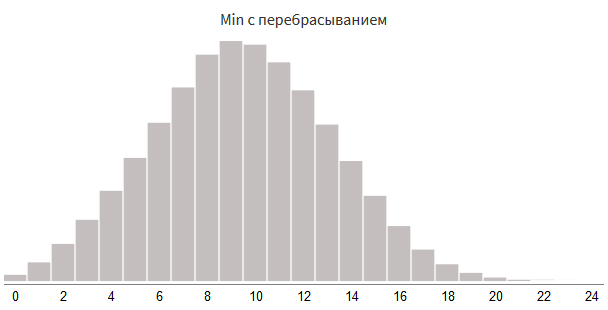
value = 0 + rollDice(3, 8)
# Max с перебрасыванием:
value = max(value, 0 + rollDice(3, 8))
# Критический бонус:
if random(100) < 15:
    value += 0 + rollDice(7, 4)

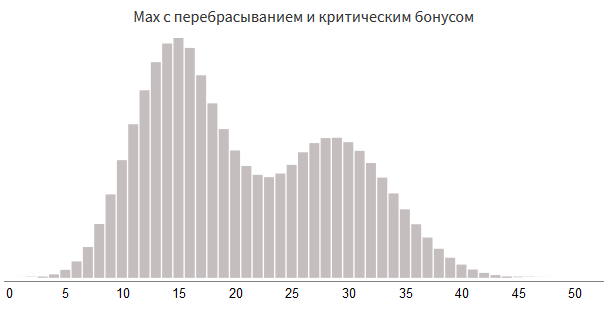
Существует множество других способов структурирования случайных чисел, но надеюсь, эти примеры дали понятие о том, насколько уже гибка система. Стоит посмотреть также на этот калькулятор бросков урона. Однако иногда сочетаний бросков кубиков недостаточно.

Произвольные формы

Мы начали с входных алгоритмов и изучения соответствующих им выходных распределений. Нам пришлось перебирать множество входных алгоритмов, чтобы найти нужный нам результат на выходе. Есть ли более прямой способ получения подходящего алгоритма? Да!

Давайте сделаем наоборот и начнём с нужных нам выходных данных, представленных в виде гистограммы. Попробуем сделать это на простом примере.

Предположим, мне нужно выбирать из 3, 4, 5 и 6 в следующих пропорциях:

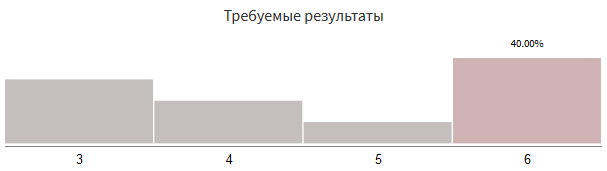
Это не соответствует ничему, что можно получить бросками костей.

Как написать код для этих результатов?

x = random(30+20+10+40)
if      x < 30:        value = 3
else if x < 30+20:     value = 4
else if x < 30+20+10:  value = 5
else:                   value = 6

Изучите этот код и разберитесь, как он работает, прежде чем переходить к следующим шагам. Давайте сделаем код более общим, чтобы его можно было использовать для разных таблиц вероятностей. Первый шаг — это создание таблицы:

damage_table = [   # массив (вес, урон)
    (30, 3),
    (20, 4),
    (10, 5),
    (40, 6),
];

В этом написанном вручную коде каждая конструкция if сравнивает x с общей суммой вероятностей. Вместо того, чтобы писать отдельные конструкции if с заданными вручную суммами, мы можем циклически перебирать все записи таблицы:

cumulative_weight = 0
for (weight, result) in table:
    cumulative_weight += weight
    if x < cumulative_weight:
        value = result
        break

Последнее, что нужно обобщить — сумму записей таблицы. Давайте вычислим сумму и используем её для выбора случайного x:

sum_of_weights = 0
for (weight, value) in table:
    sum_of_weights += weight

x = random(sum_of_weights)

Объединив всё вместе, мы можем написать функцию для поиска результатов в таблице и функцию для выбора случайного результата (можно превратить их в методы класса таблицы урона):

function lookup_value(table, x):
    # считаем, что 0 ≤ x < sum_of_weights
    cumulative_weight = 0
    for (weight, value) in table:
        cumulative_weight += weight
        if x < cumulative_weight:
            return value

function roll(table):
    sum_of_weights = 0
    for (weight, value) in table:
        sum_of_weights += weight

    x = random(sum_of_weights)
    return lookup_value(damage_table, x)

Код генерирования чисел из таблицы очень прост. Для моих задач он был достаточно быстрым, но если профайлер сообщает, что он слишком медленный, попробуйте ускорить линейный поиск двоичным/интерполяционным поиском, таблицами поиска или методом псевдонимов. См. также метод обратного преобразования.

Рисуем собственное распределение

Этот способ удобен тем, что позволяет использовать любую форму.

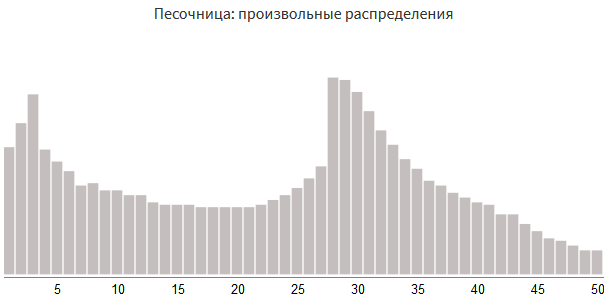
damage_table = [(53,1), (63,2), (75,3), (52,4), (47,5), (43,6), (37,7), (38,8), (35,9), (35,10), (33,11), (33,12), (30,13), (29,14), (29,15), (29,16), (28,17), (28,18), (28,19), (28,20), (28,21), (29,22), (31,23), (33,24), (36,25), (40,26), (45,27), (82,28), (81,29), (76,30), (68,31), (60,32), (54,33), (48,34), (44,35), (39,36), (37,37), (34,38), (32,39), (30,40), (29,41), (25,42), (25,43), (21,44), (18,45), (15,46), (14,47), (12,48), (10,49), (10,50)]

С помощью этого подхода мы можем выбрать распределение, соответствующее любому игровому процессу, не ограниченное распределениями, создаваемыми бросками костей.

Заключение

Случайные броски урона и случайные атрибуты реализуются просто. Вы, как гейм-дизайнер, должны сами выбирать свойства, которыми будет обладать конечное распределение. Если вы будете использовать броски кубиков:

• Для управления дисперсией используйте количество бросков. Малое количество соответствует высокой дисперсии, и наоборот.
• Для управления масштабом используйте смещение и размер кости. Если вы хотите, чтобы случайные числа находились в интервале от X до Y, то при каждом из N бросков должно получаться случайное число от 0 до (Y-X)/N, после чего к нему прибавляется X. Положительные смещения можно использовать для бонусов урона или бонусов атрибутов. Отрицательные смещения можно использовать для блокировки урона.
• Для более частых значений больше или меньше среднего используйте асимметрию. Для бросков атрибутов чаще требуются значения выше среднего, их можно получить выбором максимального, лучшего из трёх или перебрасыванием минимального значения. Для бросков урона чаще требуются значения ниже среднего, их можно получить выбором минимального или критическими бонусами. Для сложности случайных встреч с врагами тоже часто используются значения ниже среднего.

Подумайте о том, как должно варьироваться распределение в вашей игре. Бонусы атаки, блокировка урона и критические удары можно использовать для варьирования распределения с простыми параметрами. Эти параметры можно связать с предметами в игре. Воспользуйтесь «песочницей» в оригинале статьи, чтобы понаблюдать, как эти параметры влияют на распределения. Задумайтесь о том, как должно работать распределение при повышении уровня игрока; см. на этой странице информацию об увеличении и уменьшении дисперсии со временем при вычислении распределений с помощью AnyDice (о которой есть отличный блог).

В отличие от игроков в настольные игры с костями, вы не ограничены распределениями на основе сумм случайных чисел. С помощью кода, написанного в разделе «Попробуем создать собственное распределение», вы можете использовать любое распределение. Можете написать визуальный инструмент, позволяющий рисовать гистограммы, сохранять данные в таблицы, а затем отрисовывать случайные числа на основе этого распределения. Можете изменять таблицы в формате JSON или XML. Можно также редактировать таблицы в Excel и экспортировать их в CSV. Распределения без параметров обеспечивают большую гибкость, а использование таблиц данных вместо кода позволяет выполнять быстрые итерации без повторной компиляции кода.

Существует множество способов реализации интересных распределений вероятностей на основе простого кода. Сначала определитесь с теми свойствами, которые вам необходимы, а затем подбирайте под них код.

Автор: PatientZero

Источник