Как и обещал в предыдущей статье, речь в этой статье пойдет о представлении в асинхронном виде операций над адресами. В качестве примера опишу операцию дешифрации адреса. Сразу же хочу предупредить инсинуации, с которыми столкнулся после опубликования предыдущей статьи. Речь пойдет о целиком и полностью асинхронном устройстве. И прошу, не надо ссылаться на реферат узбекского университета. Якобы асинхронный дешифратор можно получить из синхронного с помощью нехитрых манипуляций. Заодно вопрос тем, кто утверждает, что асинхронный процессор произведен 20 лет назад. Как это удалось без асинхронного дешифратора?
Итак, об асинхронном дешифраторе. После размышлений я пришел к выводу, что единственный вменяемый путь синтеза асинхронного дешифратора это поэтапное удвоение разрядности адреса с помощью схемы надстройки над двумя дешифраторами вдвое меньшей разрядности. Доказать что альтернативного пути нет я не берусь. Но могу утверждать что альтернативный путь (если он есть) куда более затратен по количеству добавляемых новых сигналов.
Ввиду изложенного, речь в этой статье пойдет о двухразрядном дешифраторе. Как удвоить разрядность асинхронного дешифратора, тема следующей статьи.
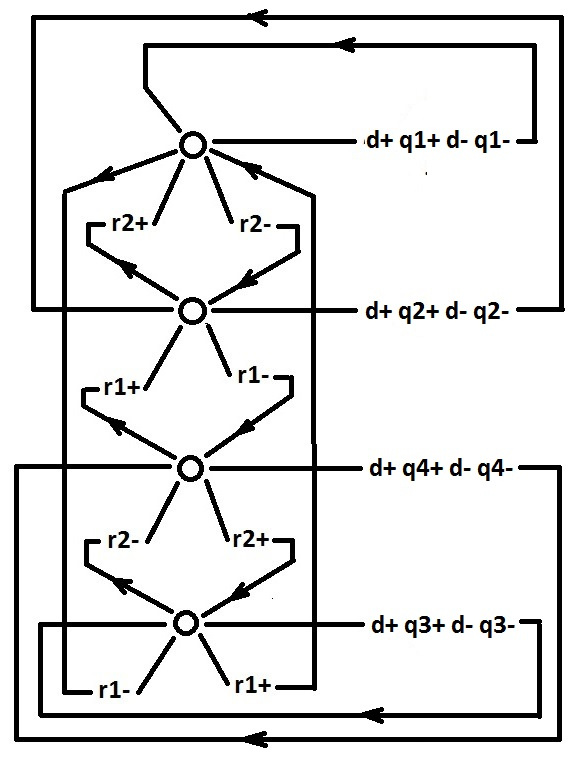
Итак, опишем исходное поведение двухразрядного асинхронного дешифратора. Как ни странно, это не сложно сделать на языке STG, и дело тут даже не в маленькой разрядности.
Входные сигналы:
d — сигнал — команда на операцию дешифрации адреса;
r1, r2 — сигналы разрядов регистра адреса.
Выходные сигналы:
q1 — переключается если r1=1 и r2=1;
q2 — переключается если r1=1 и r2=0;
q3 — переключается если r1=0 и r2=1;
q4 — переключается если r1=0 и r2=0.
Поэтапно выполнение операции дешифрации выглядит следующим образом:
0. Когда сигнал d равен 0, внешняя управляющая схема (ВУС) произвольным образом переключает сигналы r1 и r2. Схема дешифратора (СД) не отслеживает изменения сигналов r1 и r2.
1. ВУС вырабатывает сигнал d+, команду на операцию дешифрации. К этому моменту ВУС устанавливает сигналы r1 и r2 в какое-то конкретное значение. ВУС обеспечивает, что до окончания операции дешифрации сигналы r1 и r2 менять свое значение не будут.
2. В зависимости от значения сигналов r1 и r2, СД вырабатывает один из сигналов: либо q1+, либо q2+, либо q3+, либо q4+.
3. ВУС вырабатывает сигнал d-.
4. СД вырабатывает один из сигналов в соответствии с пунктом 2: либо q1-, либо q2-, либо q3-, либо q4-. Этот сигнал является сигналом окончания операции дешифрации. После этого ВУС снова может изменять сигналы r1 и r2 произвольным образом.
Немного рассуждений о том как была синтезирована схема двухразрядного асинхронного дешифратора. По сути она представляет из себя два, происходящих параллельно, «выбора по уровню» (для каждого из сигналов r1 и r2). Подробнее о «выборе по уровню» можно прочитать здесь. Затем альтернативные ветви в двух параллельных процессах попарно синхронизируются. В результате получаются четыре альтернативные ветви. В приведенном графе скорректированного итогового поведения видны только четыре альтернативные ветви. Но это дань языку STG. Описывать на нем реально происходящие процессы крайне не удобно. Все вышеуказанные «выборы по уровню» и «синхронизации альтернативных ветвей» зашифрованы в данном поведении.
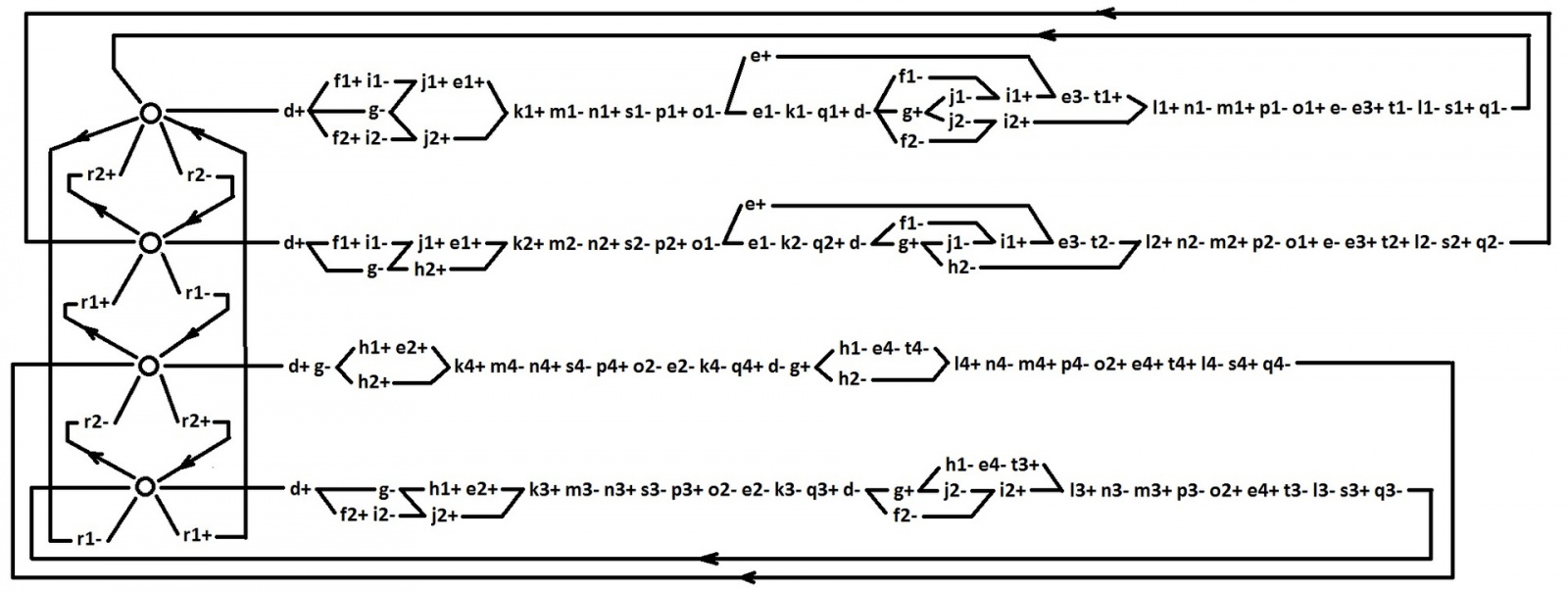
Можно добавить что синтезированное поведение не результат каких-то озарений. Это результат целенаправленного применения методологии, обзорно представленной здесь. Для каждого нового сигнала существует логическое обоснование его добавления.
В результате по представленному графу итогового поведения можно получить логические функции для каждого сигнала:
















































Как видно, все уравнения помещаются в базис 2И-НЕ, 2ИЛИ-НЕ.
А вот собственно и сама SI схема двухразрядного асинхронного дешифратора.
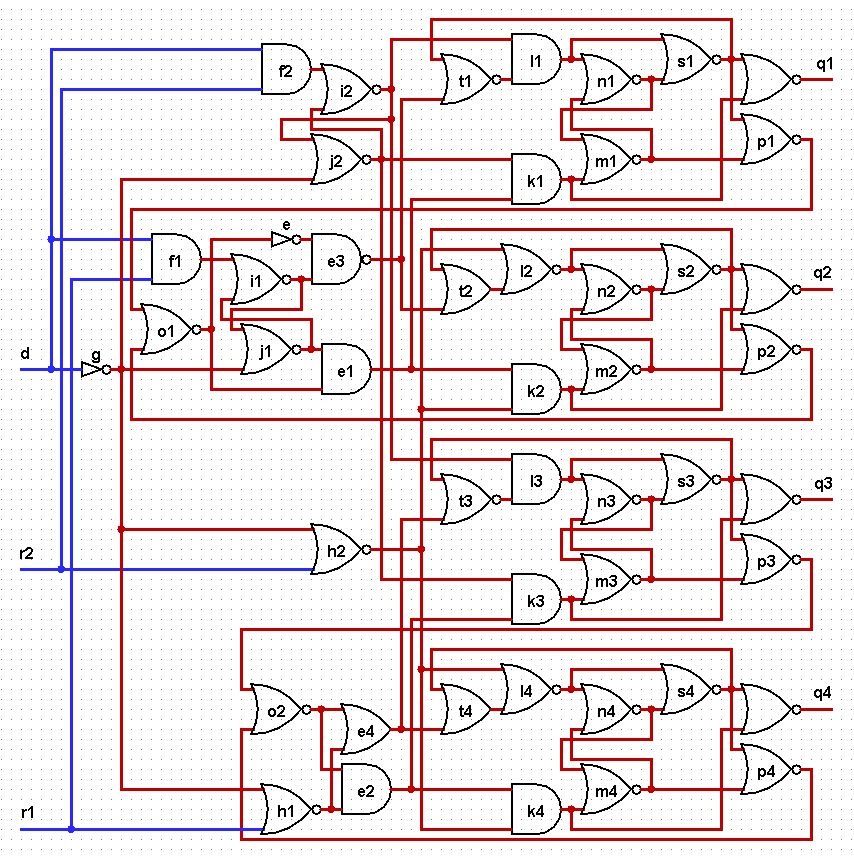
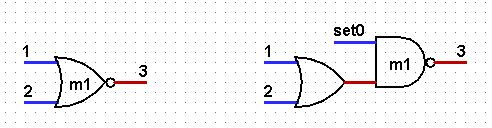
У меня нет возможности проверить схему в реальном воплощении. Но если кто-то этим заинтересуется, я буду это только приветствовать. Чтобы произвести начальную установку, надо входной сигнал d установить в 0. Внутренние сигналы m1, m2, m3, m4 надо установить в 1. Чтобы не выходить из двухвходового базиса, сделать это можно следующим образом для каждого из элементов m1, m2, m3, m4.
Элемент слева преобразуется в подсхему справа. Входные сигналы r1, r2 можно установить произвольным образом.
Автор: ajrec