Полистал недавно книжку (не всю, только то что позволили):

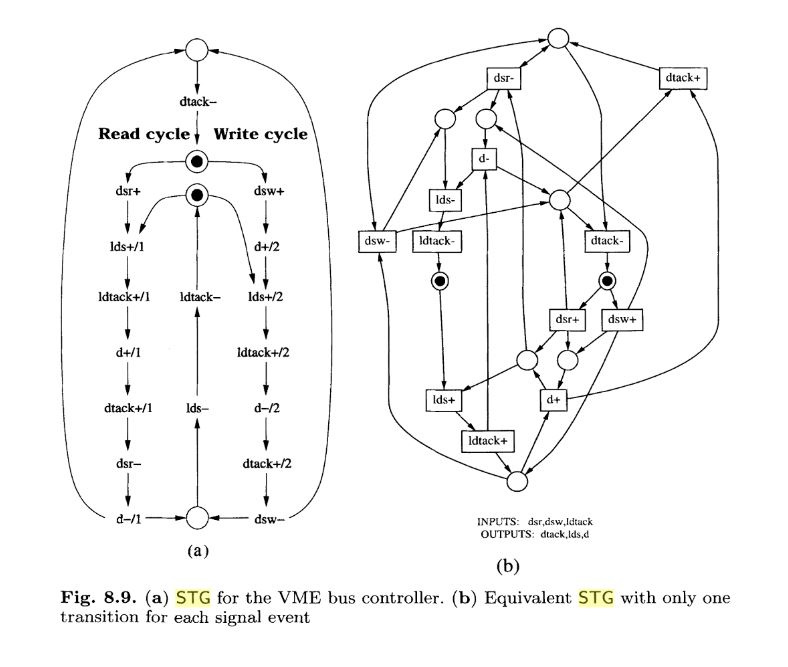
Нашел пример, как делать схемы с помощью Petrify. Исходное задание выглядит так:
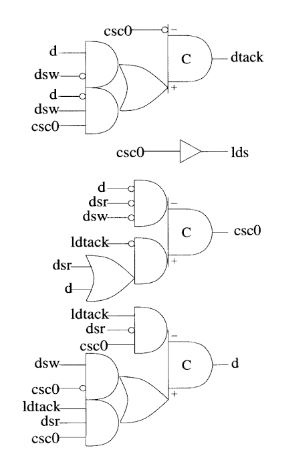
В результате получилась вот такая SI схема:
Да, от Маллера ушли не далеко, ну только что C-элементы подвесили. Думаю, все-таки надо показать, как надо делать асинхронные схемы. Для начала лучше ознакомиться с этим.
А здесь разберу приведенный пример.
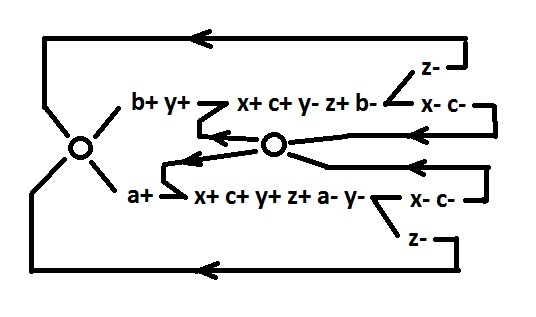
Для начала нарисую исходное поведение поудобнее и заменю длинные имена сигналов:
dsr — a
dsw — b
ldtack — c
lds — x
d — y
dtack — z
Чтобы синтезировать SI схему на двухвходовых элементах, надо дополнить исходное поведение новыми сигналами так, чтобы каждый невходной сигнал (f) можно было бы вписать в один из следующих шаблонов (или в их комбинацию):
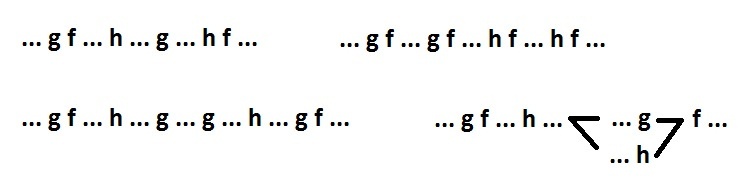
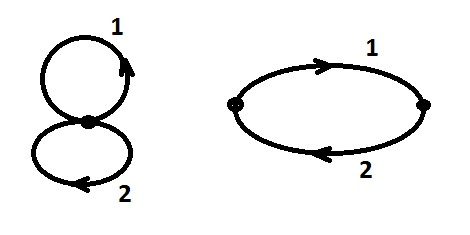
Чтобы понять, как пользоваться шаблонами применительно к поведению с выбором, рассмотрим поведение, состоящее из двух альтернативных ветвей. А потом рассмотрим поведение из тех же двух ветвей, но расположенных последовательно друг за другом.
Нетрудно проверить, что логические функции для обоих этих поведений одни и те же. Это и понятно, второе поведение это то же что и первое, только с зафиксированной дисциплиной переключений входных сигналов. Соответственно, чтобы использовать шаблон применительно к поведению с выбором, нужно последовательно хотя бы один раз пройти по всем ветвям в произвольном порядке (но только таком, который допускает исходное задание). И еще одно замечание: дополнительные сигналы будут вставляться без фиксации знака. Знаки будут расставлены в самом конце.
Итак, посмотрим на исходное поведение. Проблема, которую нужно решить в первую очередь: выбор происходит одновременно с параллельной ветвью x- c-. Необходимо синхронизировать эту ветвь. Имея в виду дальнейшее дробление поведения, лучше синхронизацию сделать отдельно для каждой альтернативной ветви. а заодно и изолировать сигнал c.
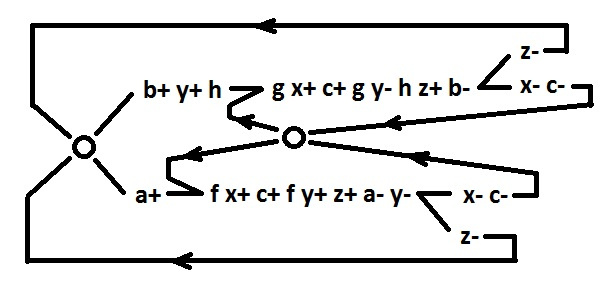
Добавленный сигнал f вписывается в шаблон (т.е. имеет двухвходовую реализацию) с помощью уже имеющихся сигналов (f= ac). Сигнал g можно было бы вписать в шаблон с помощью сигналов y и c, но лучше добавить сигнал h, который позже можно будет использовать для изоляции сигнала y. Сигналы f, g объявляем псевдовходными, т.е. запрещаем перед ними ставить новые сигналы (чтобы не испортить двухвходовую реализацию).
Исследуемое поведение четко разделяется на две альтернативные ветви. Поэтому его можно разделить на два независимых поведения, каждое из которых будет представлять из себя одну из альтернативных ветвей. Для этого нужно изолировать сигналы, встречающиеся в обеих ветвях. Изолировать сигнал x — значит получить двухвходовую реализацию (вписать в шаблон) для этого сигнала x и для всех сигналов-следствий (сигналов, переключения которых являются следствием переключения сигнала x). Таким образом мы устраним влияние сигнала x на схему и далее его можем не рассматривать.
Общими для обеих ветвей являются сигналы — c, x, y, z. Сигнал c — входной, реализации не требует. Его следствия f, g уже реализованы. Следствия сигналов x и z — входные сигналы, для них реализация не требуется. Для следствий сигнала y используем h и новый сигнал i (h=yb, i=yb). Сигналы h и i теперь псевдовходные. Для реализации сигнала y вставим новые j и k (y=jk). Сигнал z реализуем с помощью уже имеющегося сигнала i и нового сигнала m (z=im). Для реализации сигнала x добавим новые сигналы n и p (x=np). Сигналы y, z, x — теперь псевдовходные.
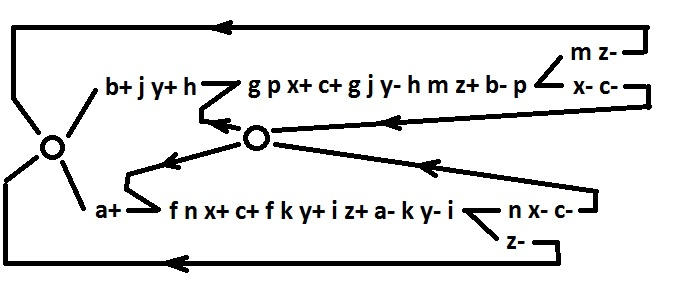
Удалим из графа изолированные сигналы. Действия такие же, как при добавлении сигнала, только последовательность обратная. Основание для удаления сигналов следующее: чтобы синтезировать схему для поведения с изолированными сигналами, достаточно построить схему для того же поведения, но с удаленными изолированными сигналами.
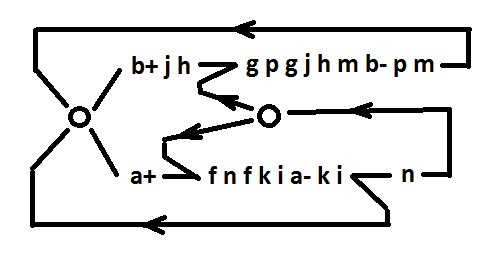
Сигналы a, b — входные, f, g, h, i — псевдовходные.
Чтобы синтезировать схему для такого поведения (с уникальными сигналами в каждой ветви), достаточно синтезировать две схемы для каждой альтернативной ветви по-отдельности. То что ветвь n параллельна точке выбора, не является препятствием, т.к. эта ветвь синхронизирована псевдовходным сигналом g.
Рассмотрим отдельно верхнюю ветвь.

Сигналы b, g, h — входные или псевдовходные.
Рассмотрим готовность к декомпозиции. Нарушений CSC нет. Сигнал m уже имеет двухвходовую реализацию (m=ph). Для сигнала j в качестве дуального можно использовать сигнал g. Для сигнала p необходимо добавить дуальный сигнал q.

Теперь найдем логические функции. Пока знаки не расставлены — вид функции условный.
m=qh
p=bq
q=gp
j=g+bp или j=g+bq
Проведем декомпозицию j (тем самым введем новый сигнал r).
j=rg
r=bp или r=bq

Запомним, что r может быть следствием p (вместо — q). Это может пригодиться при расстановке знаков.
Теперь рассмотрим отдельно нижнюю ветвь.

Сигналы a, f, i — входные или псевдовходные.
Нарушения CSC есть. Это последовательности: n f n f и k i a- k i a+. Устраняется единственно возможным способом (сигнал s).
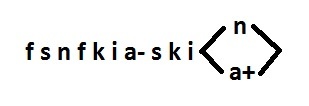
Сигналы n, k уже имеют двухвходовую реализацию (n=si, k=fs). Для сигнала s необходим дуальный сигнал t.
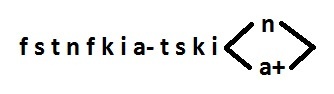
Теперь логические функции выглядят так:
n=ti
r=fs
s=ft
t=as
Для обеих альтернативных ветвей все сигналы приведены к реализуемости в двухвходовом базисе. Теперь восстановим поведение в полном объеме, со всеми добавленными сигналами.
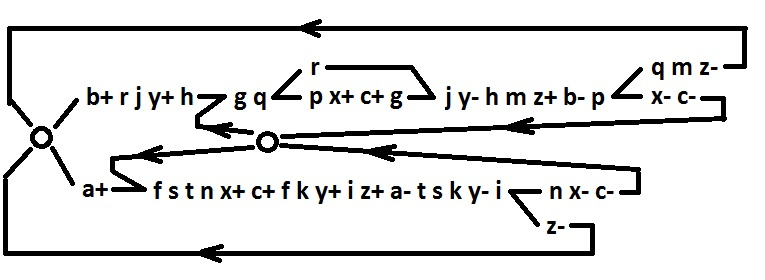
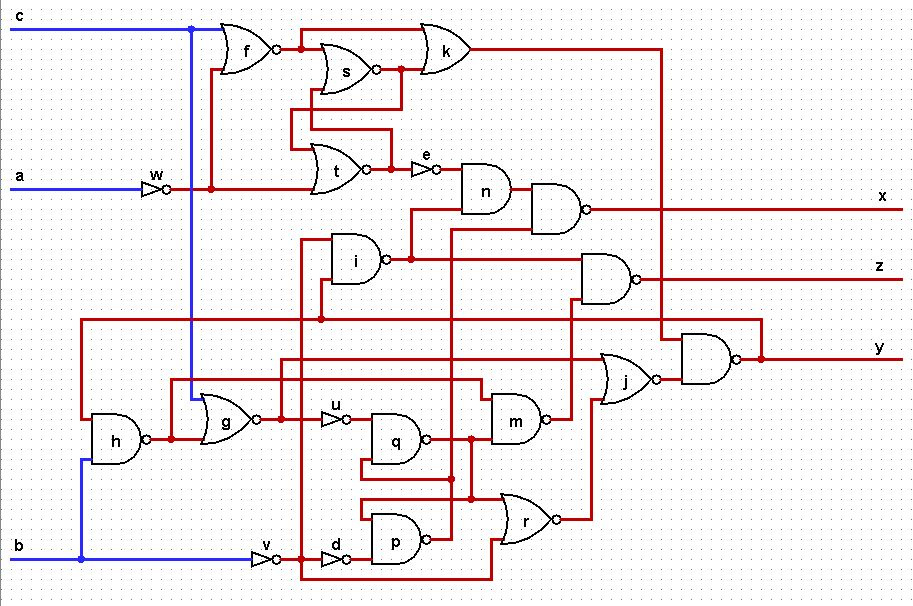
И наконец, расставим знаки. Возникшие рассогласования входов для сигналов i, f, q, p, n исправляются добавлением инверторов v, w, u, d, e соответственно.
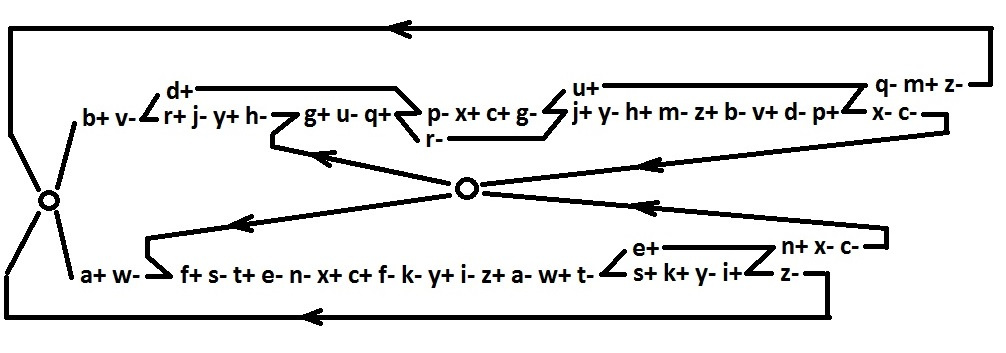
А вот логические функции для всех сигналов.
Схема выглядит так:
Посчитал транзисторные пары. Оглушительного превосходства не получилось. 78 на 94, если не ошибся. Ну, да ладно. Зря старался, что ли. Публикую.
Автор: ajrec