В предыдущем посте “Cascadeur — можно ли заменить каскадеров?” мы обещали подробнее рассказать про концепцию программы и про инструменты, позволяющие аниматорам создавать физически корректные движения персонажей.
В классической анимации законы физики нарушаются ради усиления эффекта и выразительности. Свободное обращение с законами физики и даже создание своих законов, к которым зритель привыкает — это важный инструмент анимации. Но такой стиль воспринимается зрителем как “мультяшный”.
А что будет, если в анимации строго соблюдать законы Ньютона и использовать только те анимационные приемы, которые не противоречат этим законам? Такая физическая корректность сама по себе не даст реализма, но может дать эффект целостности. Ведь в этом случае персонаж движется в пространстве строго в соответствии с нашими законами физики, он обладает массой, инерцией и все его движения обусловлены силами.
Уже давно физическое моделирование используются для реалистичной анимации пассивных конструкций: столкновение твердых тел, движение тканей, волос и т.д. Вряд ли кто-то поспорит с тем, что делать анимацию ткани вручную неоправданно сложно. Логично было бы применять физическое моделирование и в анимации тела персонажей.
Но как рассчитывать реалистичное движение персонажа, который, в отличие от пассивных конструкций, сам порождает силы, приводящие части тела в движение? Как аниматору добиться того, чтобы это движение не противоречило законам физики?
При изучении этого вопроса удалось выделить 3 понятия, правильное обращение с которыми гарантирует соблюдение законов Ньютона:
- Точки опоры
- Центр масс
- Момент импульса
Если по отношению к этим понятиям соблюдать определенные правила, то этого достаточно, чтобы даже сложный объект (с сотнями степеней свободы) подчинялся законам Ньютона целиком. Это конечно не снимает с аниматора заботу о выразительности, естественности и других характеристиках движения.
Так как в большинстве движений сопротивлением воздуха можно пренебречь, то правила можно сформулировать следующим образом:
1) Если у персонажа нет точек опоры, то:
- Центр масс движется по баллистической кривой (параболе), независимо от того какие движения совершает персонаж.
- Момент импульса сохраняется постоянным, независимо от того какие движения совершает персонаж. То есть ни ось вращения, ни количество вращения не могут измениться, пока у персонажа нет точек опоры.
2) Если же точки опоры есть, то:
- Любое изменение траектории центра масс означает, что на него действует сила равная силе воздействия персонажа на опору (например, на пол) и направленная в противоположную сторону.
- Любому изменению момента импульса соответствуют определенные силы воздействия в точках опоры, которые не должны противоречить ограничениям опоры. Например, давление на пол может быть направлено вниз, но не вверх.
Соблюдение этих правил превращается в непростую задачу для каждого движения. Обычно приходится изучать движение, чтобы понять, как оно делается в реальности.
Но даже если решение найдено, то напрашивается специальный инструмент, позволяющий управлять центром масс и моментом импульса напрямую, а это уже обратная задача динамики, и она требует итерационных методов решения. На итерационных методах и построены все алгоритмы в Cascadeur’е.
Основной итерационный метод, используемый для моделирования физики и большинства инструментов — численное интегрирование Верле. Главная особенность метода — возможность накладывать несколько различных ограничений на систему и итерационно находить решения, удовлетворяющие всем ограничениям. На этом мы, возможно, остановимся подробнее в одном из следующих постов.
Персонаж в нашей системе состоит из вершин, обладающих массой, и связей, соединяющих вершины. При редактировании кадра любые манипуляции с персонажем похожи на действия с физическим объектом в вязкой среде.
Этот подход позволил нам реализовать следующие возможности и инструменты в Cascadeur’е:
- Можно двигать персонажа за любую вершину, при этом положение связанных вершин будет меняться, так как они являются частью общей системы.
- Вершину можно закрепить, тогда манипуляции с соседними вершинами не повлияют на ее положение.
- Центр масс можно двигать — тогда сдвигаются все вершины, которые не закреплены. Если есть закрепленные вершины, то поза персонажа изменится.
- Центр масс можно закрепить — тогда движение любой вершины приводит к такому движению незакрепленных вершин, при котором центр масс останется на месте.
- Для центра масс можно автоматически построить баллистическую траекторию исходя из начальной и конечной позиции.
- Момент импульса можно “сглаживать” и делать неизменным на интервале. Это меняет положение и позу персонажа в каждом кадре.
- Момент импульса можно закрепить. Тогда сдвиг любой вершины приведет к такому повороту всего персонажа относительно центра масс, при котором момент импульса останется неизменным.
- У вершин, центра масс и момента импульса траектории движения унифицированы (заданы простыми массивами координат) и к ним можно применять различные фильтры.
- Можно рассчитать необходимое напряжение мышц на каждом кадре и отобразить эти напряжения градацией цвета мышц. Возможность видеть распределение нагрузки на персонаже помогает оценить правильность движения.
- Можно рассчитать и отобразить вектор силы в каждой точке опоры. Это также помогает оценить правильность движения.
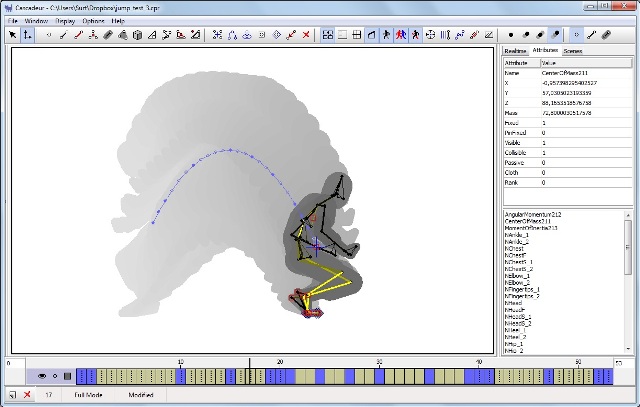
Как эти инструменты применяются в работе на примере простого прыжка можно посмотреть в этом видео:
Плюсы такого подхода:
- Анимированный персонаж воспринимается зрителем как объект с массой, а значит более реальный. В итоге легче достичь реализма.
- Движения получаются более целостными и совместимыми друг с другом, даже если сделаны разными людьми (даже с разным качеством).
- Такие движения лучше совместимы с движениями, полученными с помощью motion capture.
- Фантазия аниматора не так сильно ограничена, как при использовании motion capture. Ничто не мешает сделать движения, которые не может сделать ни один каскадер в мире.
Мы пока только развиваем этот подход и исследуем его возможности, придумываем и пробуем новые инструменты. Будем держать вас в курсе результатов наших исследований.
Автор: Nekki






