Что можно сделать с помощью двух кирпичей, обыкновенной электрической плитки и тепловизора на Arduino ? Сэкономить кучу электричества! Как все эти вещи взаимосвязаны, можно узнать из данной статьи. По ходу дела пришлось затронуть некоторые вещи из ТАУ (теория автоматического управления), но я постарался избавиться от занудной математики и подробно объяснить роль «тепловизора менее чем за 100$» в процессе.

Внимание! Под катом есть одна очень «толстая», но красивая картинка! И много текста!
Сегодня, практически у каждого в хозяйстве имеются электронагревательные приборы — плитки, чайники, обогреватели ну и кипятильники на худой конец. В целом принцип их работы можно описать так — ток течет по нихромовой нити и вызывает ее нагрев, а также нехило мотает электросчетчик. Все нагревательные приборы очень много «кушают» электричества, так уж повелось. Однако и здесь есть выход!
Дело в том, что любое тело, обладает своей собственной «тепловой инерционностью», и здесь можно привести может и не совсем точную, но понятную аналогию с большим круглым булыжником:
Представим, что булыжник нужно откатить на расстояние десять метров. Можно сразу навалиться на него всем весом, на протяжении всего участка толкать что есть сил, и таким образом переместить его до нужного места. А можно сначала усилием сдвинуть его, и далее лишь слегка подталкивать. Разумеется, во втором случае, мы устанем меньше. Так вот по аналогии первый способ — это включение нагревателя напрямую в сеть, а второй — использование энергосберегающих алгоритмов управления.
А это означает, что мы можем подать на вход электронагревательного элемента напряжение специальной формы, что позволит достичь нужной температуры, но с меньшими затратами электроэнергии (кВт*ч). Разумеется, при этом экономия не берется из воздуха. А появляется она за счет увеличения времени нагрева, и чем больше время — тем соответственно больше экономия! Как рассчитать такое управление — долгая история и в рамках данной статьи это будет затронуто лишь поверхностно (ибо матан).
Итак, возьмем, например, для исследования обыкновенную электроплитку, мощностью в 1 кВт. И положим на нее два силикатных кирпича — для повышения той самой «тепловой инерционности» (а как Вы уже поняли, чем эта условная величина больше, тем грандиознее процент экономии). Вот эта красавица:

Согласен, выглядит не очень! Она много повидала на своем веку, и, тем не менее продолжит служить во имя науки и дальше.
Для расчета энергосберегающего управления для данного электронагревательного прибора во-первых, нужно выполнить задачу составления его простейшей математической модели. Она может быть, например, дифференциальным уравнением или, как в данном случае, передаточной функцией. Говоря языком википедии, передаточная функция является дифференциальным оператором, выражающим связь между входом и выходом линейной стационарной системы. И зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал.
У электронагревательных приборов входной величиной является действующее значение напряжения, а выходной — температура объекта. И имея на руках передаточную функцию теплового объекта, мы можем, подав на вход напряжение в 220В, на выходе получать значение температуры, а значит, владеть самой настоящей математической моделью.
Открыв любой учебник по ТАУ, можно убедиться, что разновидностей передаточных функций существует великое множество. Так как же узнать какая из них наиболее точно опишет объект исследования? Для этого необходимо провести своеобразное «опознание», по научному — идентификацию объекта. Звучит серьезно, а на практике выглядит так: включить в сеть и замерить температуру на протяжении всего времени нагрева. Вот что получится в случае с электроплиткой:
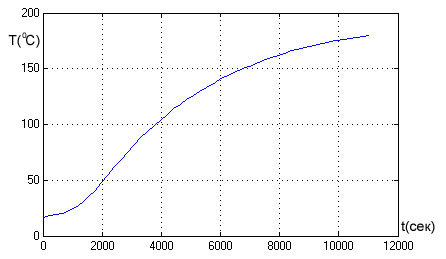
Исходя из вида функции, смело можно сделать вывод, что электроплитка точно описывается передаточной функцией, под названием апериодическое звено второго порядка. Вот так она выглядит:
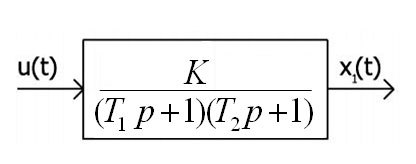
Здесь входная величина U(t) обозначает напряжение, которое может быть как постоянным во времени (220В, имеется в виду действующее значение), так и изменяющимся по какому либо закону. Выходная величина x(t) — температура. Из картинки можно понять, что у данного звена есть свои параметры — K, T1 и T2, которые называются соответственно коэффициентом усиления и постоянными времени. Как следует из их названий, значение K отражает величину изменения сигнала, прошедшего через такое звено, а постоянные времени напрямую зависят от той самой «тепловой инерционности» объекта. Эти коэффициенты можно приблизительно вычислить из предыдущего графика. И, очевидно, что они влияют на точность математической модели, а значит и на величину сэкономленной электроэнергии.
Забегая вперед, скажу — для данной плитки уже не один год студенты рассчитывали то самое энергосберегающее управление (поэтому она такая потрепанная). И раз за разом, для идентификации объекта (ну чтобы получить тот график сверху) располагали термопару строго посередине между кирпичами. Ну и возник закономерный вопрос — а что если взять и переместить датчик температуры в совсем другое место, как изменятся параметры объекта? Каждый раз проводить опыт с различным положением термопары было бы чрезвычайно долго — как можно понять из графика выше, один эксперимент идет почти три часа. И тут в самый раз подходит использование того самого тепловизора на Arduino.
Главный недостаток только что упомянутого устройства — долгое время получения изображения в инфракрасном диапазоне здесь практически не играет роли — эксперимент идет очень долго по сравнению с временем сканирования. Но в результате, получается не один график изменения температуры в одной точке, а целых 768! В соответствии с разрешением термограммы 32x24 пикселя.
Таким образом, используя тепловизор, был произведен подобный эксперимент по идентификации объекта — 25 термограмм было снято за несколько часов. Область сканирования охватывала практически всю боковую поверхность кирпичей, как показано на картинке:

А вот так выглядит процесс нагрева в инфракрасном диапазоне (этакий инфракрасный time-lapse):
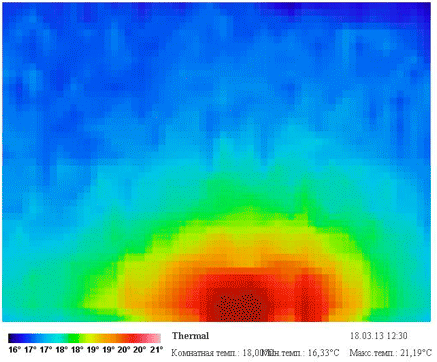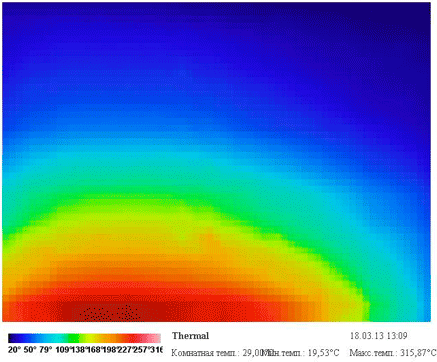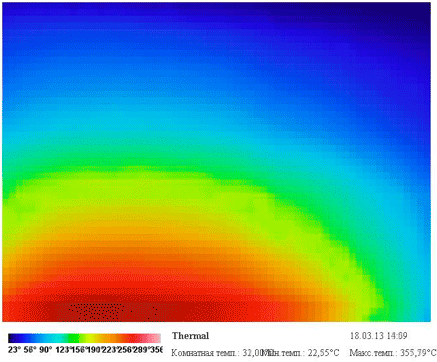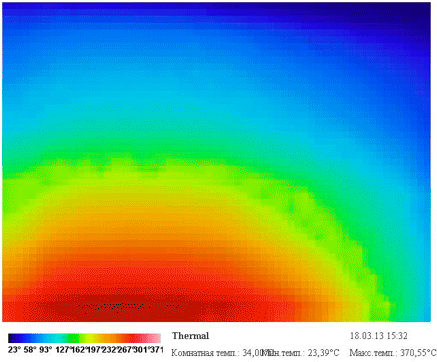
Стоит обратить внимание, что ложные цвета в термограмме назначаются автоматически в зависимости от максимальной и минимальной измеренной температуры, и градиент соответствия также динамически меняется.
Открытием стало то, что центр нагрева смещен влево, хотя камера была направлена строго по центру кирпичей. Вероятно, это происходит из-за неоднородностей внутри нижнего кирпича, либо конструкцией нагревательного элемента плитки.
Тепловизор на базе Arduino работает следующим образом — сначала составляется пространственная матрица температур, затем по ней уже визуализируется картинка в ложном цвете. Это оказалось огромным плюсом — так как на выходе системы есть не только красивая картинка но и файл матрицы, которая и играет главную роль в исследовании. Взяв навскидку пять точек на таких матрицах (их 25), можно отследить динамику изменения температуры:

Вот так будут выглядеть графики переходных процессов (так эти зависимости температуры от времени называются) в пяти выбранных точках и с термопары для сравнения:
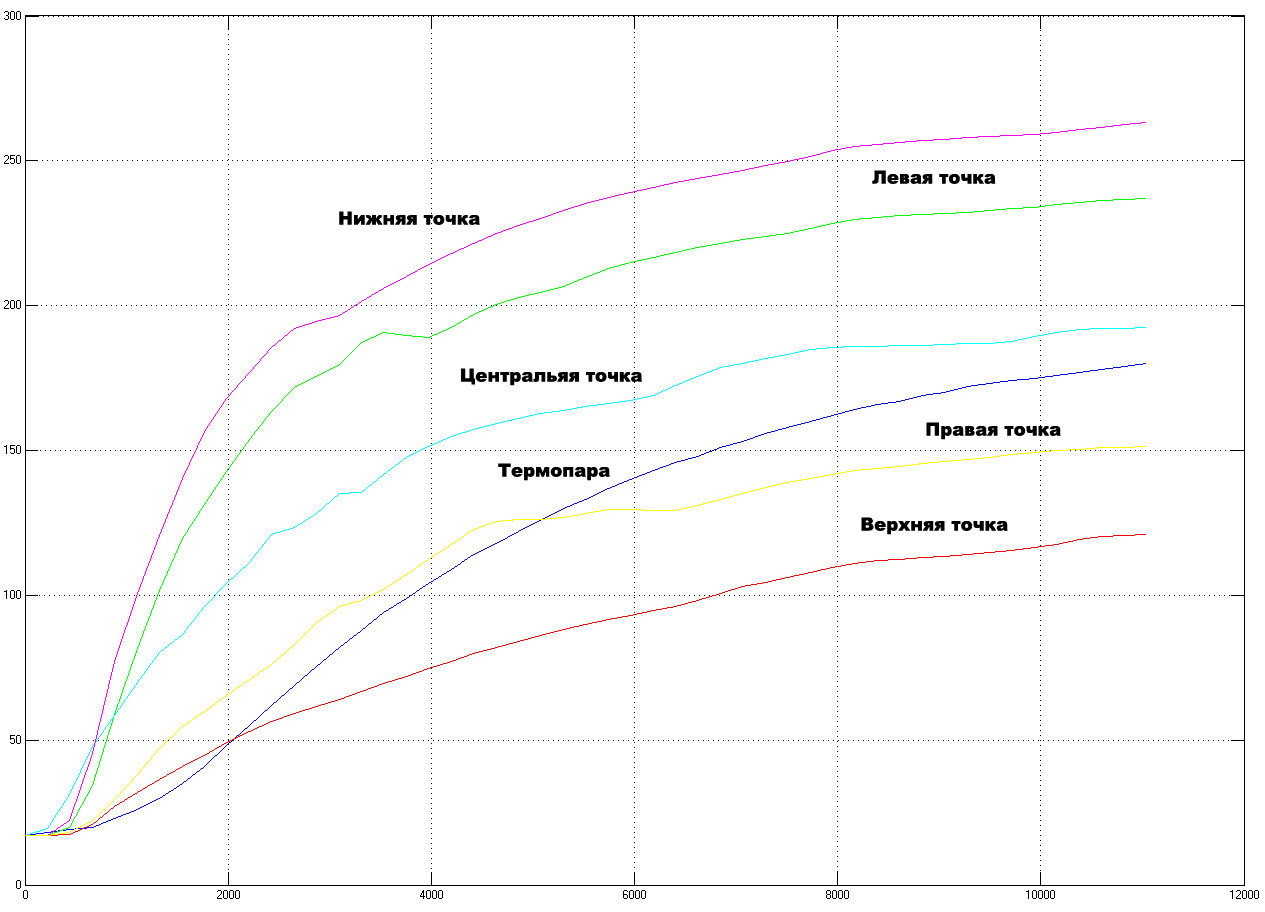
Графики с тепловизора более корявые, так как основаны всего навсего на 25 точках, тогда как данные с термопары поступают каждые две секунды. Кроме того, невооруженным взглядом можно отметить различие в графиках температуры с термопары и тепловизора. Возможно это связанно с физическим различием методов измерения — если термопара расположена как-бы «внутри» объекта, то инфракрасный датчик тепловизора сканирует именно поверхность, на которую в свою очередь влияют процессы испарения влаги и конвекция воздуха.
Далее из этих графиков можно получить те самые коэффициенты (К, Т1 и Т2) для создания математической модели электроплитки. Однако на этот раз, у нас будет не одна, а целых шесть моделей!
Опустив математическую часть стоит отметить, что в процессе исследования была замечена интересная особенность — значения коэффициентов зависят от расположения точки на термограмме относительно предполагаемого центра нагрева — эта та красная область внизу термограммы. Причем зависимость их практически линейная:
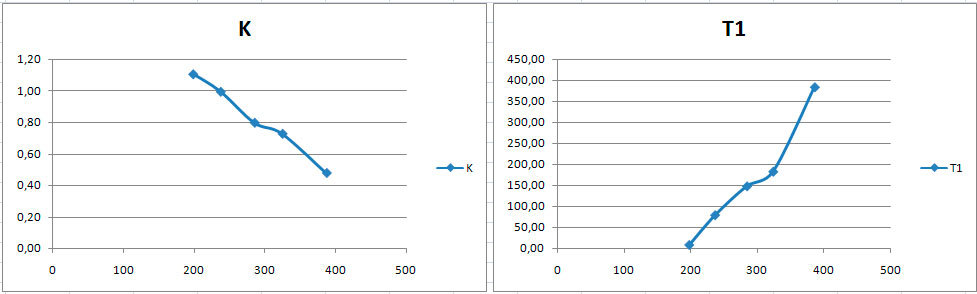
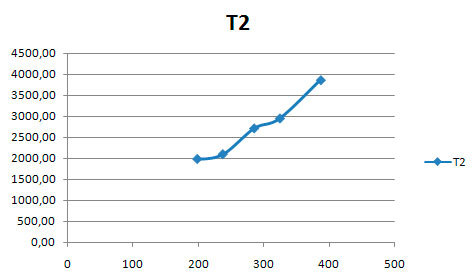
А так как известно, что графики не лгут, ориентируясь на положении точки измерения в принципе, можно определить коэффициенты практически для любой точки объекта, не прибегая к построению графиков для всех 768 точек.
И тем не менее, из этих пяти ранее выбранных точек, лучшие результаты в экономии энергии показала левая точка. В составе системы с регулятором, настроенным на основе данных, полученных из этой точки:
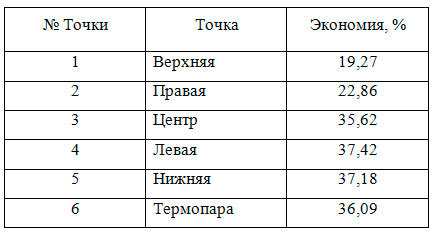
Процент экономии считается по сравнению с энергией, потраченной на нагрев электроплитки до 80 градусов путем простого включения в розетку. Как должно изменяться напряжение на электроплитке, чтобы сэкономить почти 40% электроэнергии, можно посмотреть на данном графике:
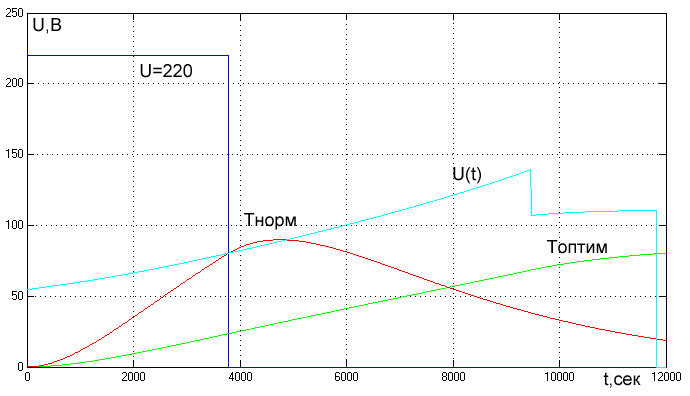
Здесь оптимальное управление обозначено U(t), соответствующая температура плитки при таком управлении — T(оптим). Для сравнения также приведены графики напряжения и температуры плитки при простом включении в сеть. Как видно, экономия получается за счет увеличения времени нагрева почти в три раза.
Подводя итоги:
Итак, если Вас всю статью мучал вопрос, зачем нужно греть кирпичи на плитке и считать какую то мифическую экономию, если на практике это никому не нужно, то вот вам достойный ответ: дело в том что данная плитка является прямым аналогом такого объекта исследования как печь сопротивления. Этот промышленный монстр мощностью в 800 кВт (например) потребляет не просто много, а катастрофически много электричества. И соответственно энергосбережение очень к месту.
Тепловизор в данном случае сыграл огромную роль, позволив построить наиболее полную картину процессов, происходящих при работе электронагревательных приборов, и на основе этих данных получить еще более точную с точки зрения энергосбережения модель объекта, а кроме того, найти наконец, серьезное применение в качестве полноценного устройства.
Автор: Astrei






