Целью физики как классической науки является изучение закономерностей нашего мира. Большинство таких закономерностей уже достаточно изучены, чтобы применять их в повседневной жизни. И современные физики решили изменить масштаб исследований, как в одну, так и в другую сторону.
Рассмотрим две фундаментальные физические теории. Первая из них – хорошо знакомая всем общая теория относительности. Теория относительности отвечает на вопросы происхождения и развития Вселенной и хорошо объясняет крупномасштабное поведение космоса. Вторая — квантовая механика — напротив, добилась большого успеха в объяснении физики микромира. Объединим эти две теории и получим практически полную картину Вселенной: от межъядерных взаимодействий до поведения галактик.
Однако в получении единой картины мира есть одна загвоздка: эти масштабные теории, подтвержденные множеством расчетов и экспериментов, полностью несовместимы между собой. У каждой теории свои основы, свои математические и физические принципы. Применение квантовой механики к галактическим взаимодействиям, как и использование теории относительности для изучения ядерных взаимодействий приводит к абсурдным результатам. Выход один: придумать новую теорию, которая бы согласовывалась как с теорией относительности, так и с квантовой механикой, и в то же время объединяла их. Создание единой теории всего сущего – главная задача физиков со времен Эйнштейна. Одним из кандидатов на звание единой теории и является теория струн.
Немного истории
Началось все, как обычно, с математики. В 18 веке знаменитый математик Леонард Эйлер занимался изучением свойств функций, которые сам же и придумывал. Одна из таких функций получила название бета-функции Эйлера. Выглядит она так:
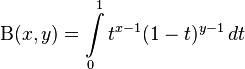
Не так уж сложно для людей, знакомых с интегральным исчислением. Эйлер описал свойства функции, и, не найдя практического применения, на два века бета-функция была забыта.
В 1968 году молодой физик Габриель Венециано, работающий в швейцарском ЦЕРНе, случайно обнаружил, что все свойства частиц, участвующих в ядерном взаимодействии, можно описать с помощью бета-функции Эйлера. Формула отлично работала для описания взаимодействий частиц, но никто не понимал почему. Если взять знаменитую формулу Эйнштейна, то ее физический смысл можно выразить фразой «энергия пропорциональна массе». У формулы Эйлера физического смысла не было – просто переменные, при присваивании которым определенных значений получался результат, согласующийся с экспериментом. Через два года такой смысл был найден – физики обнаружили, что если заменить элементарные частицы колеблющимися одномерными струнами, то взаимодействие таких струн как раз и представляется в виде формулы Эйлера. Одномерность означает, что толщина такой струны по сравнению с длиной бесконечно мала.
Поскольку струны достаточно малы, то они выглядят как элементарные частицы, следовательно, не противоречат уже проведенным экспериментам. Сейчас теория струн сильно изменилась по сравнению с изначальным видом, однако основная идея осталась такой же.
Струны как механизм работы Вселенной
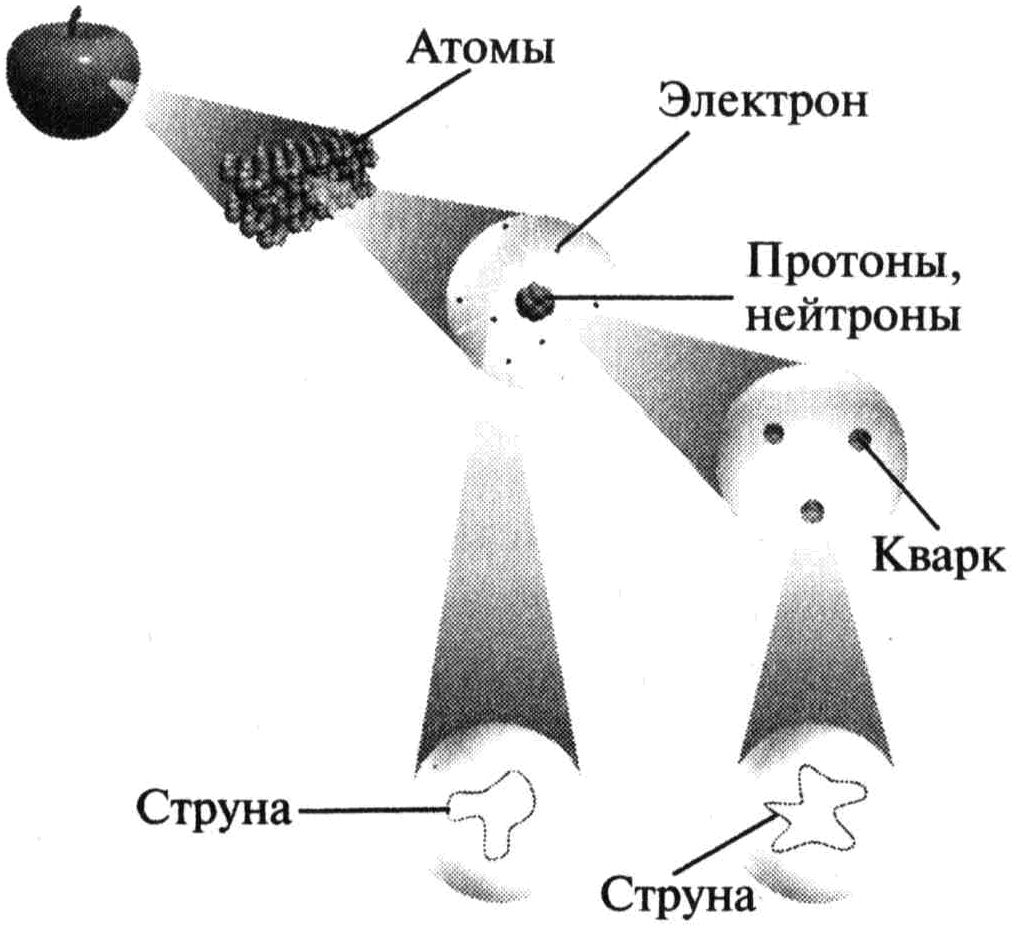
Эта картинка достаточно хорошо изображает представления типичного обывателя о теории струн. В действительности же все обстоит с точностью до наоборот: из теории струн следует все, она отлично согласуется как с квантовой механикой, так и с теорией относительности. Вдобавок к этому, теория также находит объяснение гравитации, которое ищется со времен Ньютона. Такая многогранность перевешивает некоторую абсурдность идеи о том, что вся материя состоит из мельчайших струн.
Для объяснения основной идеи теории струн одномерные струны можно представить в виде привычных для нас струн музыкальных инструментов. Возьмем, к примеру, гитару. Колебание каждой струны обладает двумя важными свойствами:
1. Амплитудой, ответственной за громкость звука.
2. Частотой, которая определяет высоту звука.
Звуки, частоты которых различаются менее на 1 Гц, практически неразличимы для человеческого уха. Чем больше частота звука, тем менее уловимы изменения этой частоты. Поэтому в музыке разность частот соседних нот варьируется от 1 Гц для низких звуков до нескольких сотен герц для высоких звуков. В целом, для исполнения музыкальных произведений мы получаем только определенный ограниченный набор частот, соответствующих принятым нотам. Мы можем сыграть ми с частотой 330 Гц или фа с частотой 349 Гц, но частоты между ними в музыке нам недоступны. Такой конкретный вид колебания называется модой, а совокупность всех возможных мод – спектром колебаний.
От громкости звука и моды его колебания зависит энергия колебания. Интуитивно можно понять, что громкий и высокий звук обладает большей энергией, чем тихий и низкий. А теперь дадим нашу гитару в руки Эйнштейну, который заметит, что энергия вообще-то говоря пропорциональна массе. В теории струн как раз и используется это соотношение: масса элементарной частицы определяется энергией колебаний ее струны.
Используя более абстрактные рассуждения, физики установили, что существуют и другие связи между модой струны и характеристиками частицы, такими как заряд, отклик частицы на гравитационное воздействие и т.д. Более того, тот же принцип справедлив не только для свойств частиц, но и для самих частиц. Фотоны, глюоны, u-мезоны и другие экзотические частицы являются всего лишь различными модами колебаний одинаковых струн.
Это приводит к следующему выводу: зная все возможные моды колебания струны, «ноты», которые на ней можно сыграть, мы могли бы объяснить все свойства всех элементарных частиц. Серьезная заявка на единую теорию поля, не правда ли?
Девятимерная гитара
Рассмотрим нашу гитару со стороны гитариста. Конструкция гитары позволяет струнам колебаться только в некоторых определенных направлениях. Можно ударить по струнам сверху-вниз или снизу-вверх, либо оттянуть струну от себя и отпустить. Если бы струна была закреплена между двумя точками в свободном 3-хмерном пространстве, количество возможных направлений колебаний бы увеличилось. Имея в своем распоряжении большее число измерений, чем три, мы бы также увеличили количество возможных направлений колебаний. Однако мы жестко ограничены тремя измерениями.
Но не в теории струн. При дальнейшем исследовании возникла новая загвоздка: некоторые вычисления приводили к невозможным результатам, например, отрицательной вероятности. Физики долго бились над этой проблемой и нашли решение, с которым согласовывались все расчеты: Вселенная должна иметь десять измерений – девять пространственных и одно временное.
Если с временным измерением кое-как можно примириться, то откуда берутся еще шесть измерений, которые мы даже представить себе не можем? Эти шесть измерений являются свернутыми – они настолько малы, что в привычном масштабе мы можем не принимать их в расчет. Автомобиль, сделав круг, вернется в те же координаты в трехмерном пространстве. За этот круг он бесчисленное количество раз пересечет шесть свернутых измерений. Однако для очень малых струн координаты в свернутых измерениях начинают принимать серьезное значение.
А что дальше?
Развитие теории струн уже не остановить. Теория с десятью измерениями получила название теории суперструн. Когда измерения снова начали не согласовываться с ожидаемыми, было введено новое, одиннадцатое измерение. Так появилась М-теория: упоминание о струнах исчезло из названия, поскольку появились аналоги двумерных струн – мембраны, трехмерные, четырехмерные струны. Сложность теории увеличивается с каждым годом, но до сих пор ее развитие не зашло в тупик, и она имеет все шансы когда-нибудь стать единой теорией всего.
Что почитать?
1. Стивен Хокинг, «Краткая история времени», «Мир в ореховой скорлупке», «Теория всего» — популярным языком рассказывает о современной картине мира.
2. Брайан Грин, «Элегантная Вселенная. Суперструны, скрытые размерности и поиски окончательной теории» — отличная книга по теории струн без лишней физики.
3. Митио Каку, «Введение в теорию суперструн» — серьезный учебник для тех, кто знает физику и хочет знать еще больше.
Автор: Wakes
