На Хабре периодически появляются статьи и комментарии о чудесах квантовой физики: квантовом ластике и слабых измерениях. К сожалению, слишком часто о них говорят как о загадочных и непонятных явлениях, позволяющих творить чуть ли не магию, хотя на самом деле нет в них ровным счетом ничего удивительного. В этом посте я перевожу статью Шона Кэрролла о квантовом ластике с отложенным выбором. Пусть он будет отправной точкой для обсуждения в комментариях всяких хитростей квантовой механики.
От переводчика. Шон Кэрролл — профессор в Caltech, занимающийся космологией и основами квантовой физики. Он последовательный сторонник многомировой интерпретации (ММИ) квантовой механики, о которой недавно выпустил книгу Something Deeply Hidden. Соответственно, объяснение эксперимента в посте будет с позиций ММИ. Хотя по большому счету это не столь важно для самого объяснения. Вы можете почитать мой недавний пост про ММИ, если хотите освежить в памяти основы.
А еще Кэрролл ведет прекрасный подкаст Mindscape. Этот подкаст оказался без малого главным событием моей интеллектуальной жизни в последний год, и, честное слово, это лучшее, что вы можете вынести из этого поста.
Disclaimer! Я местами адаптировал немного текст, и чуть-чуть добавлял от себя для пущей ясности. Все ошибки на моей совести (и в личке, надеюсь).
Эта статья — глава из книги Something Deeply Hidden, не вошедшая в финальный вариант текста.
Давайте представим, что вы студент-физик, сидите на курсе по экспериментальной работе, а профессор в особенно плохом настроении. Она заставляет вас проводить особенно странную версию опыта Юнга, объясняя, что эта версия называется «квантовый ластик с отложенным выбором». Кажется, вы что-то такое видели на YouTube однажды.
В традиционном опыте Юнга с двумя щелями пучок электронов проходит через две щели и попадает на регистрирующий экран. Каждый электрон по отдельности оставляет точку на экране, но если мы подождем, пока наберется много таких событий, мы увидим интерференционную картинку со светлыми и темными полосами. Это происходит потому, что волновая функция электронов проходит через обе щели и интерферируют сама с собой.
Если мы измерим, через какую щель проходит каждый электрон, интерференционная картинка исчезнет, и мы увидим сглаженное распределение на экране. Учебники по квантовой механики традиционно нам расскажут, что это произошло из-за коллапса волновой функции при ее наблюдении нами на щелях. Многомировая интерпретация говорит, что это потому что электрон перепутался с измерительным прибором, а прибор — с окружением (произошла декогеренция), и волновая функция разделилась на два отдельных мира, в каждом из которых электрон прошел только через одну из щелей.
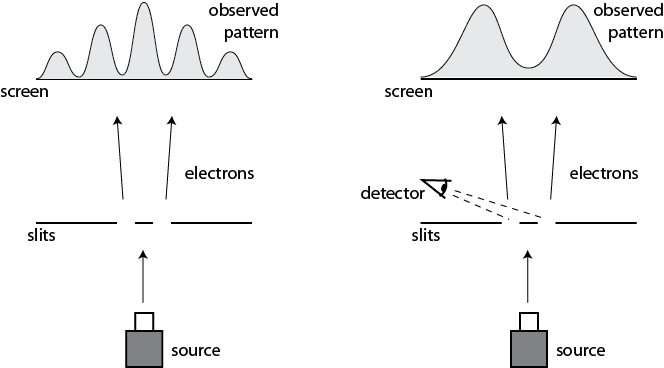Интерференционная картинка видна когда электрон проходит через две щели (слева), пока не производится попытка измерить, через какую именно щель проходит электрон (справа).
Ваш же эксперимент усложнен: вы будете измерять, через какую щель проходит электрон, но не с помощью большого макроскопического прибора, а с помощью квантового прибора, и хранить информацию в кубите. Например, на каждый «главный» электрон, проходящий через щели, у нас есть второй «вспомогательный» электрон, запутанный с первым. Пара запутанна следущим образом: если главные электрон проходит через левую щель, вспомогательный электрон оказывается в состоянии со спином вверх, а если через правую — со спином вниз:
Ψ = (Л)[↑] + (П)[↓].
Ваш профессор, кто очевидно не в настроении сегодня, настаивает, чтобы бы не производили измерения над «вспомогательными» электронами, и даже не давали им улететь и врезаться во что-нибудь в комнате. Вы аккуратно ловите и храните их, например, в магнитной ловушке.
Что же мы увидим на экране, если повторим такой эксперимент со многими электронами? Конечно, сглаженное распределение без интерференционной картинки, конечно. Интерференция может возникнуть только если две части являются составляющими одной и той же волновой функции, а раз два главных электрона теперь запутаны с вспомогательными, пути через левую и правую щель оказываются различимыми, и мы не видим интерференционной картинки. В этом случае оказывается безразлично, что у нас не было настоящего измерения (и декогеренции), а лишь запутанность. Важно только то, что главные электроны оказались в состоянии запутанности с вспомогательными электронами. Любая запутанность убивает интерференцию.
Конечно, мы можем измерить спины вспомогательных электронов, если захотим. Если мы измерим их вдоль вертикальной оси, мы получим [↑] или [↓]. В отношении квантового состояния Ψ это поместит нас либо во вселенную, где главный электрон прошел через левую щель, либо во вселенную, где он прошел через правую. Наконец, если мы повторим эксперимент множество раз, мы не увидим интерференции.
Ладно, говорит, ваш профессор с садистскими наклонностями, потирая руки со злодейской ухмылкой. Давайте теперь измерим наши вспомогательные электроны, но не по вертикальной, а по горизонтальной оси. Состояние в вертикальном и горизонтальном базисах связаны как:
[↑] = [→] + [←],
[↓] = [→] – [←].
(Для простоты мы отбросим нормировочные факторы). В этом базисе то же состояние, что сверху будет выглядеть так:
Ψ = (Л)[→] + (Л)[←] + (П)[→] – (П)[←]
= (Л + П)[→] + (Л – П)[←].
Когда мы измеряли вспомогательный спин в вертикальном направлении, мы получали определенный путь главного электрона: [↑] был запутан с (Л), а [↓] был запутан с (П). Производя измерение, мы узнавали, прошел ли главный электрон через левую или правую щель. Теперь же мы измеряем спин вдоль горизонтального направления, и эта определенность исчезает. После измерения мы вновь оказываемся в ветви волновой функции, где главный электрон проходит сразу через две щели. Если мы измерили спин «лево», главный электрон получит фазовый сдвиг при прохождении через правую щель (знак минус), но это чисто математическая особенность.
Итак, выбирая такой способ измерения, мы «стерли» информацию о том, через какую щель прошел электрон. Это так называемый «квантовый ластик». Сам процесс стирания не меняет общего распределения точек на экране. Оно остается гладким, и интерференции не возникает: результаты измерения «влево» и «вправо» по-прежнему случайны.
Но теперь у нас есть не только общее распределение электронов на экране. Для каждой точки на экране мы знаем также результат измерения для вспомогательного электрона: был он в состоянии «спин налево» или «спин направо». Так-с, расцветает ваш профессор, давайте теперь пойдем к компьютеру и разделим наши измерения на две части: часть, для которой вспомогательный электрон имел спин налево, и часть, для которой он был направо. Что мы теперь увидим?
Любопытно, что теперь интерференция снова возникает. Главные электроны, ассоциированные с вспомогательными электронами с левым спином, формируют интерференционную картинку, так же как и те, для которых вспомогательный электрон имел спин влево. (Помните, что интерференционная картинка возникает не сразу, а появляется по мере набора статистики одиночных электронов). Но эти две картинки оказываются сдвинуты друг относительно друга, так что пики в одной картинке совпадают с провалами в другом. При их наложении друг на друга возникает гладкое распределение там, где на самом деле спрятана интерференционная картинка.
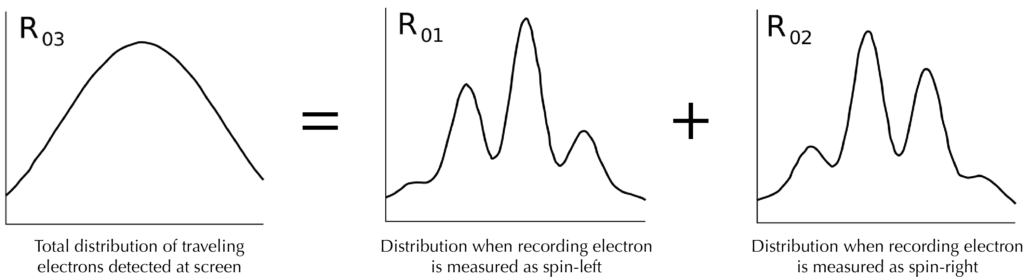Взято с Wikipedia
Оглядываясь назад, мы не найдем это таким уж удивительным. Если посмотреть на то, как состояние Ψ было записано относительно вспомогательных электронов в горизонтальном базисе (спином налево или направо), мы увидим, что каждое измерение было запутанным с главным электроном, проходящим через обе щели. Так что конечно интерференция могла возникнуть. И тот минус, казавшийся совершенно неважной математической деталью, сдвинул одну картинку относительно другой так, что при их наложении они сложились в гладкую картинку.
Ваш профессор, кажется, удивился этому больше, чем вы. «Разве вы не видите!» — возбужденно восклицает она. «Если мы не измеряем вспомогательные электроны вовсе, или измеряем их по вертикальной оси, никакой интерференции не возникает. А если мы измеряем их вдоль горизонтальной оси, оказывается, там была скрытая интерференция, которую мы смогли обнаружить, разделив результаты измерения на части для разных спинов вспомогательного электрона.»
Вы и другие студенты согласно киваете, хоть и находитесь в некотором недоумении.
«Подумайте о том, что это значит! Выбор направления измерения вспомогательных спинов мог быть сделан еще уже после того, как все главные электроны были зарегистрированы на экране. Если бы мы сохранили все вспомогательные спины, не дав им запутаться с окружением, мы могли бы совершить этот выбор спустя годы.»
Кажется да, бормочет аудитория, похоже на правду.
«Но интерференция только происходит, когда главные электроны проходят через обе щели, а гладкое распределение возникает, когда электрон проходит через одну щель. Это решение — пройти через две щели или через одну — происходит задолго до того, как мы измерили вспомогательные электроны. Очевидно, наше решение измерить их горизонтально, а не вертикально, послало сигнал назад в прошлое и сообщило главным электронам, что им надо пройти сразу через обе щели, а не через одну.»
Озадаченная аудитория застывает на мгновение и взрывается в протесте. Решение? Назад в прошлое? Вы вообще о чем? Электрон не совершает выбора пройти через одну щель или другую. Его волновая функция (и все, с чем он запутан), эволюционирует с соответствии с уравнением Шредингера, как обычно. Электрон не совершает выборов, он однозначно всегда проходит через обе щели, но оказывается в запутанном состоянии. Измеряя вспомогательные электроны вдоль разных направлений, мы можем выбирать разные части запутанной волновой функции, некоторые из которых интерферируют, а некоторые — нет. Ничего не вернулось назад в прошлое. Это классный эксперимент, но никто не строит никакой машины времени тут.
Вы и ваши товарищи правы. Ваша профессор несколько увлеклась. Всегда есть искушение думать об электроне как о чем-то обладающем «свойствами волны и частицы одновременно», и Копенгагенская интерпретация квантовой механики только потворствует этому. Если мы поддадимся этому искушению, недалеко и мысль о том, что электрон при прохождении щелей ведет себя или как частица, или как волна, и в каждом эксперименте реализуется один из этих двух вариантов. А с этой позиции квантовый ластик с отложенным выбором действительно приводит к заключению, что информация должна была быть передана назад в будущее, чтобы помочь электроны с выбором. Честно говоря, в популярных объяснениях зачастую усложняют картину, создавая у квантовой механики ауру загадочности. А предположение, что квантовая механика позволяет посылать сигналы в прошлое, только подливает масла в огонь.
Всем этим искушениям надо противостоять. Электрон просто является частью волновой функции Вселенной. Он не совершает выбора быть частицей или волной. Но по какой-то причине даже серьезные исследователи основ квантовой физики иногда рассматривают эксперименты с квантовым ластиком с отложенным выбором и другие ему подобные (которые, кстати, были многажды проверены на практике) как свидетельство обратной причинности в природе — сигналы, распространяющиеся назад во времени, влияют на прошлое. Вариант такого эксперимента, предложенный никем иным, как Джоном Уилером, предполагал несколько телескопов на другой стороне экрана, которые могут определить, через какую щель прошел электрон, значительно позже момента, когда он прошел. В отличие от поздних комментаторов, Уилер не зашел столь далеко, чтобы предположить обратную причинность, и не настаивал на том, что электрон всегда является либо частицей, либо волной.
Нет никакой надобности в обратной причинности для объяснения квантового ластика с отложенным выбором. Для последователя многомировой интерпретации, результат очевиден без всяких путешествий во времени. Хитрость в том, что при запутывании с одним спином, а не огромным ансамблем частиц в классическом детекторе и окружении, электрон не декогерирует в полном смысле этого слова. Когда главный электрон запутан только с одной частицей, мы можем рассматривать разные варианты измерения этой вспомогательной частицы. Если, как обычном опыте Юнга, мы измерили щель, через которую прошел электрон с помощью классического макроскопического прибора, у нас нет такого выбора вариантов измерения. При настоящей декогеренции крошечный размер изначальной запутанности оказывается усиленным, по сути необратимо, в запутанность с окружением. В этом смысле квантовый ластик с отложенным выбором оказывается полезным мысленным экспериментом для осознания роли декогеренции и окружения при измерениях.
К сожалению, не все являются сторонниками многомировой интерпретации. В других версиях квантовой механики волновые функции и в самом деле коллапсируют, в отличие от многомировой интерпретации, где коллапс только кажущийся, возникающий из-за декогренции. В интерпретациях, где коллапс на самом деле происходит (типа GRW), он оказывается асимметричным во времени: волновый функции коллапсируют, но не могут вернутся в изначальное состояние. Если в вашей теории есть коллапс волновой функции, но при этом вы хотите сохранить общую симметрию по времени в законах физики, вы можете убедить себя в необходимости обратной причинности.
А можете принять гладкую эволюцию волновой функции с ветвлением, а не коллапсом, и автоматически сохранить симметрию по времени для всех основных уравнений без необходимости путешествий во времени или сомневающихся электронов.
Welcome to the Many Worlds!
Автор: Михаил Коробко
