
После публикации моей статьи о том, какой была бы Земля, будь она в два раза больше, у читателей появился вопрос: «А что насчёт тороидальной Земли»? Вопрос не самый оригинальный, эту тему уже обсуждали в онлайне и проводили её моделирование. Но я люблю всё делать сам, так что я попытался провести свой собственный анализ.
Может ли существовать тороидальная планета?
Стабильность тороидальной планеты неочевидна. С практической точки зрения планеты можно рассматривать как жидкие шарики без поверхностного натяжения – прочность камня не сравнить с весом планеты. Они обладают эквипотенциальными гравитационными поверхностями с учётом центробежного потенциала. Если бы это было не так, то на них встречались бы места, которые могли бы уменьшить свою энергию перетеканием в сторону понижения потенциала. Ещё один очевидный факт – существование верхней границы скорости вращения, после которой планета развалится: центробежная сила на экваторе превышает гравитацию и материал улетает в космос.
Равновесные формы вращающихся эллипсоидных планет, удерживающихся силой собственной гравитации, были всесторонне проанализированы. Началось всё с Ньютона, тогда же были проведены ранние героические экспедиции для установления формы Земли, Маклорен продолжил его дело, Якоби открыл, что при больших скоростях вращения эллипсоиды с неравными осями оказываются устойчивее сплющенных эллипсоидов Маклорена. Субраманьян Чандрасекар вёл интересные разработки в этой области. Но с тех пор появились компьютеры, и поэтому были проведены аналитические и численные подсчёты более сложных или релятивистских случаев.
Тем же образом были проанализированы равновесные формы вращающихся тороидов – это делали Пуанкаре, Софья Ковалевская, и Фрэнк Дайсон (Dyson 1893, Dyson 1893b). По крайней мере, в теории, можно раскрутить эллипсоидную планету до состояния кольца, хотя существует множество возможностей возникновения колебаний, дестабилизирующих систему, после чего происходит прыжок в кольцевое состояние.
Кольцо может быть нестабильным, в частности, из-за «узловой» нестабильности — всё большее количество массы может аккумулироваться в определённых меридианах, в результате чего произойдёт разрыв на несколько отдельных масс. Дайсон проанализировал этот случай, и обнаружил, что он имеет значение, когда R (расстояние от центра тора до центра трубы) превышает r (радиус трубы) более чем в три раза – то есть, тонкие обручи оказываются нестабильными. Существует также меньшая скорость вращения, при которой кольцо становится нестабильным и приливные силы сжимают его в эллипсоид. Так что общая масса и угловой момент должны быть правильно заданы с самого начала.
Судя по всему, законы физики не запрещают появление тороидальных планет. Просто вероятность их возникновения чрезвычайно мала, и такая планета, скорее всего, окажется нестабильной на геологических масштабах времени из-за внешних возмущений. Так что, если мы предположим, что она уже есть, возможно, из-за действий продвинутой цивилизации, эстетика которой сильнее разума – каковы будут её свойства?
Направления
Будем называть два круга, параллельных плоскости вращения, экваторами (внешним и внутренним). В случае, когда принципиальной разницы между ними для обсуждаемой темы не будет, я буду называть их просто экватором. Полюсами будут круги, наиболее удалённые от экваториальной плоскости.
Направление к центру будет обозначать направление к оси вращения, к ободу – от оси вращения. К плоскости – по направлению к экваториальной плоскости. Север – в сторону ближайшей части северного полюсного круга, юг – в сторону ближайшей части южного полюсного круга.
Гравитация тороида
Как работает гравитация на тороидальной планете?
В случае очень большого R тороидальная планета, по сути, становится цилиндрической. В этом случае гравитация убывает как 1/r, где r – расстояние от оси. Воздействие на любую секцию будет пропорционально общей массе (пропорциональной R) и гравитации (пропорциональной 1/R), так что общая сила останется постоянной с увеличением R. Её сбалансирует определённое вращение. Поверхностная гравитация 2G rho/r, где rho – масса на единицу длины. Так что пока поверхностная гравитация будет достаточно большой (с малым r) эта сила преодолеет центробежное ускорение и ничего не будет улетать проч. Но для тора с малым радиусом всё гораздо сложнее.
Я решил использовать метод Монте-Карло для оценки равновесной формы. Начав с общей массы планеты и углового момента, я распределил множество массивных, бесконечно тонких колец (потенциал взял из этого упражнения – хорошо, что в классической физике электрический и гравитационный потенциал одинаковы). Я подсчитал их общий потенциал и добавил центробежный. Это позволяет провести аппроксимацию эквипотенциальных поверхностей и «заполнять» потенциал ближе к центру тора всё большим количеством колец, до тех пор, пока их масса не станет соответствовать массе планеты. Я пересчитал угловую скорость на основе нового распределения масс. Затем повторял процесс до тех пор, пока либо планета разлетается, либо сжимается в шар, либо проходит достаточно много итераций. Это не самый элегантный метод (в литературе используется разложение в ряд тороидальных гармоник), но мне его было достаточно.
Основной результат – тороидальная планета реалистично допускает достаточно большие массу и угловой момент. Сечение получается ни круглым, ни эллиптическим, а напоминает яйцо, с немного более острой внутренней кривизной, чем снаружи.
Почему планета не сплющивается в диск? Вращение пытается расплющить планету, но ему приходится работать против местной гравитации, которая пытается сжать её в шар (или цилиндр).
Хотя в моей симуляции такие планеты оказались стабильными, разброс допустимых значений был невысок: большая часть комбинаций массы и углового момента были нестабильными. Я не анализировал сложный вопрос узловой нестабильности.
Рассмотрю здесь пухленький тороид массой равной массе Земли и небольшим центральным отверстием («Пончик»), а также более широкий, обручеподобный тороид массой с 6 земных, но более приближенной к земной гравитацией («Обруч»).
Пончик
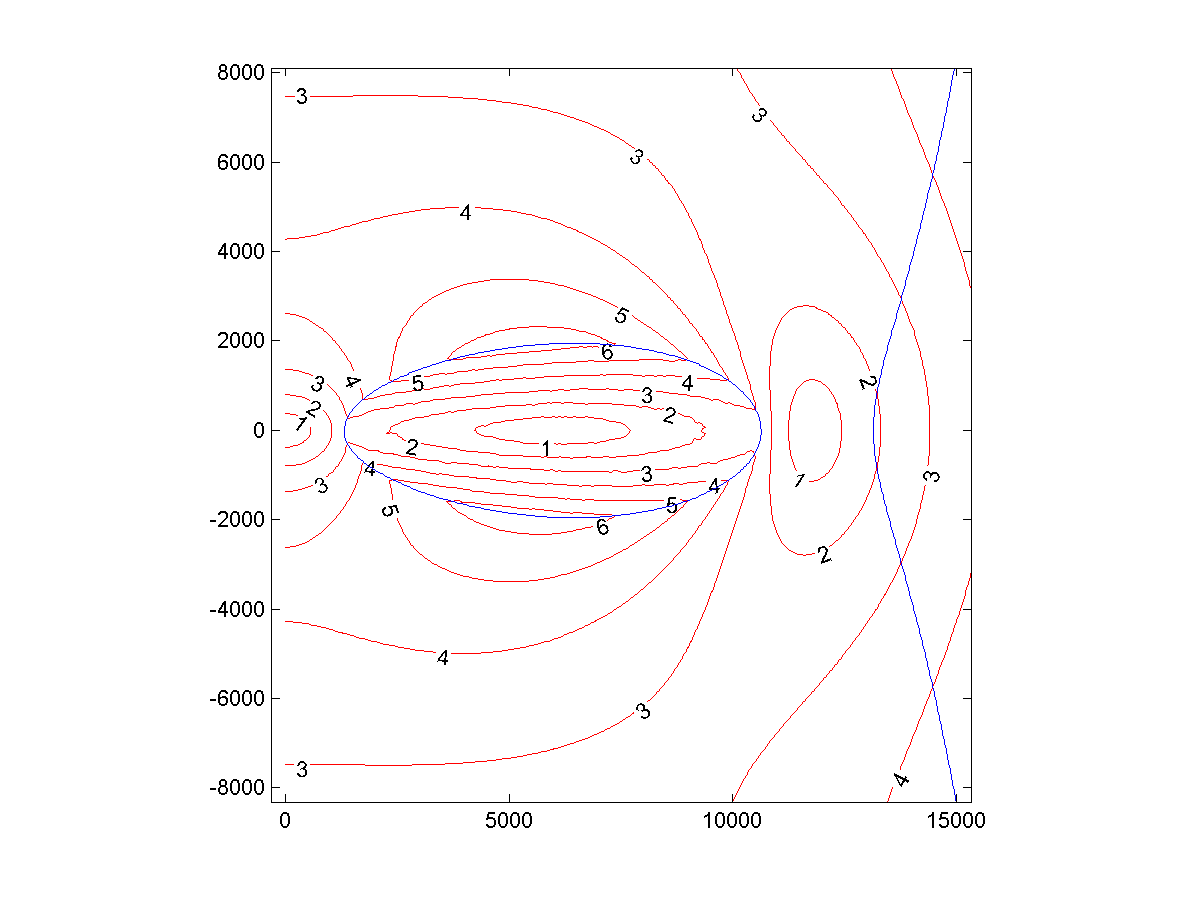
Рис. 1: локальное гравитационное ускорение (м/с2) вокруг Пончика, испытываемое объектом, вращающимся с ним совместно
Внутренний экватор Пончика отстоит от центра на 1305 км, а внешний – на 10663 км. Диаметр экватора – 9328 км.
Планета простирается на расстояние в 1953 от экваториальной плоскости, и диаметр с севера на юг равен 3906 км. Соотношение диаметров равно 2,4.
Окружность с севера на юг равна 21587 км (0,54 земной), а с запада на восток – 66809 км (1.7 земной). Общая площадь – 8,2 х 108 км2 (1,6 земной). Общий объём = 1,1 х 1012 км3, отличается от земной не более, чем на 1% (всё-таки Пончик был выбран как планета земной массы). Отношение объёма к площади – 1300, 61% от Земной – на единицу объёма площади больше.
День длится 2,84 часа.
Обруч
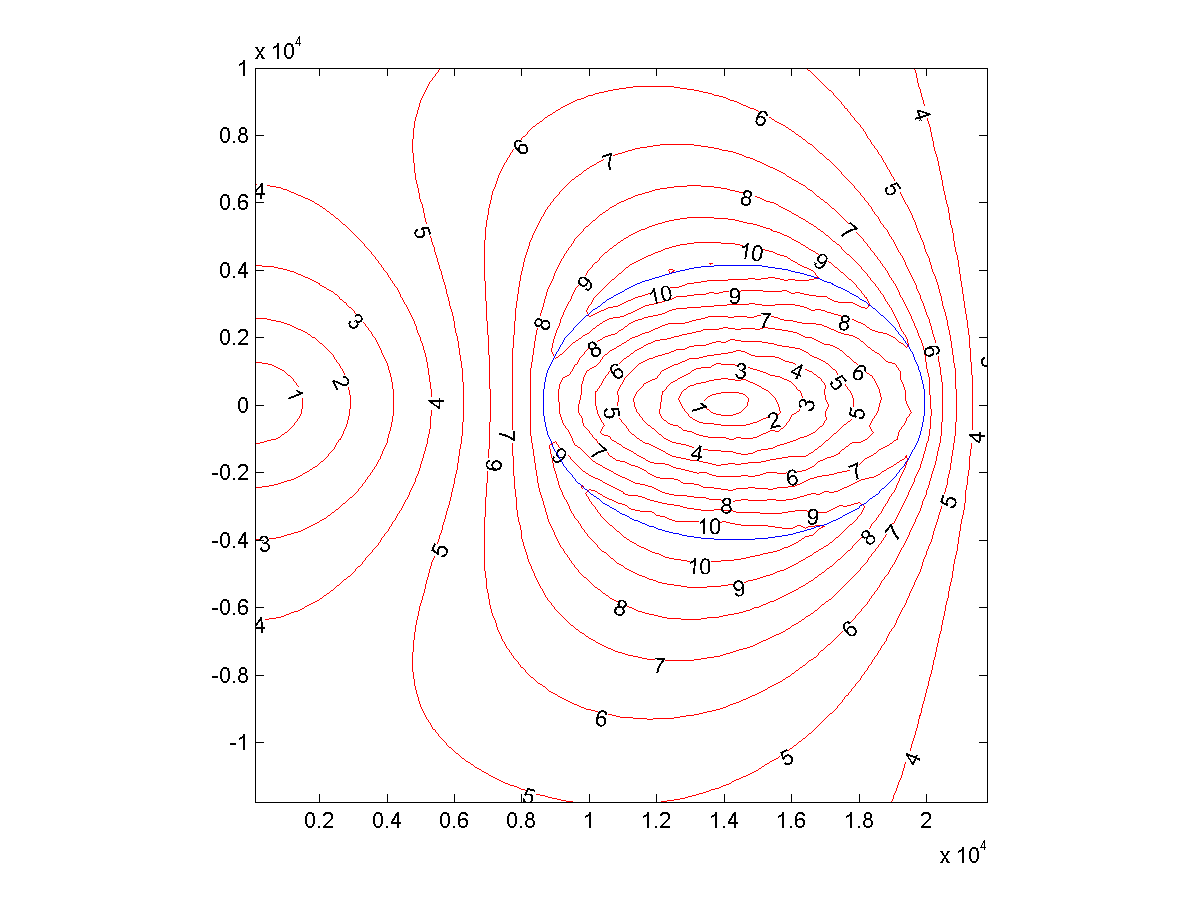
Рис. 2: локальное гравитационное ускорение (м/с2) вокруг Обруча, испытываемое объектом, вращающимся с ним совместно
Внутренний экватор Обруча отстоит от центра на 8633 км, а внешний – на 19937 км. Диаметр экватора 11304 км.
Планета простирается от экваториальной плоскости на 4070 км, диаметр с севера на юг – 8141 км. Соотношение сторон сечения примерно равно 4:3, как у старых мониторов. Радиус круга центра масс 14294 км.
Окружность с севера на юг 30794 км (0,77 земной), а с запада на восток – 125270 (3,1 земной). Общая площадь 2,5 х 109 км2, в 4,9 раз больше земной, а общий объём 6,5 х 1012 км3, в 6 раз больше земного. Соотношение объёма к площади = 150, 70% от земного.
День длится 3,53 часа.
Окружающая среда
На что похожа жизнь на тороидальной Земле?
Гравитация
Поверхностная гравитация зависит от местоположения. Самая слабая она вдоль внутреннего и внешнего экваторов, и самая сильная – рядом с полюсами, немного по направлению к центру. Это одно из основных различий.
Пончик
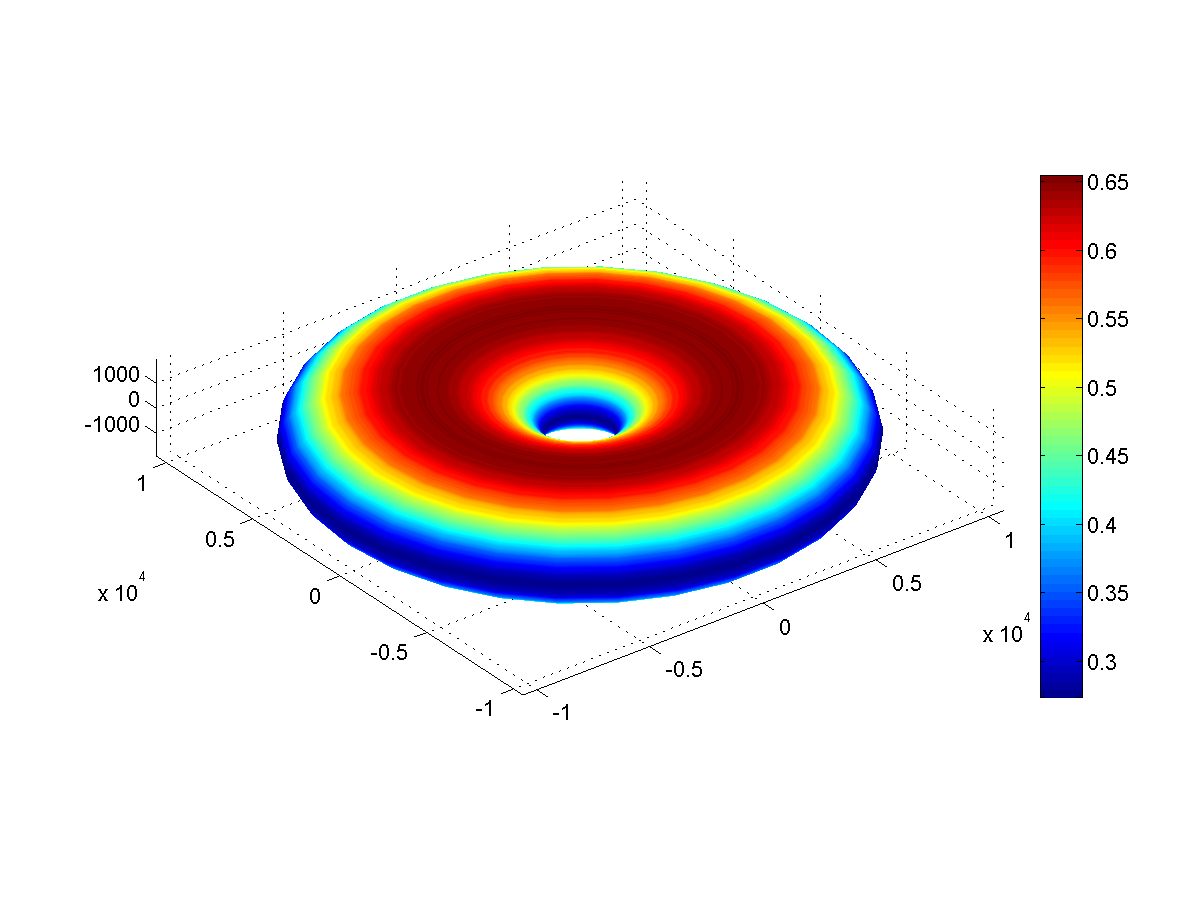
Рис. 3: гравитация на поверхности Пончика (м/с2)
На Пончике гравитация вдоль экваторов составляет всего 0,3 G, и 0,65 G вдоль полюсов. Скорость убегания не слишком отличается от Земной, и равна 11,4 км/с.
Геосинхронная орбита вокруг Пончика очень близка к внешнему экватору, менее 2000 км. Летающий по ней спутник будет оставаться над одним местом, но, в отличие от Земли, он не сможет покрывать передачами всё полушарие, только небольшой район.
С другой стороны, окружная скорость на экваторе равна 6,5 км/с, и запуски проводить проще. Ракете, запущенной на восток, требуется скорость всего в 4,9 км/с, чтобы убежать.
В середине отверстия существует нестабильная точка Лагранжа. Спутник там будет притягиваться к экваториальной плоскости, но любое отклонение от неё будет усиливаться.
Обруч
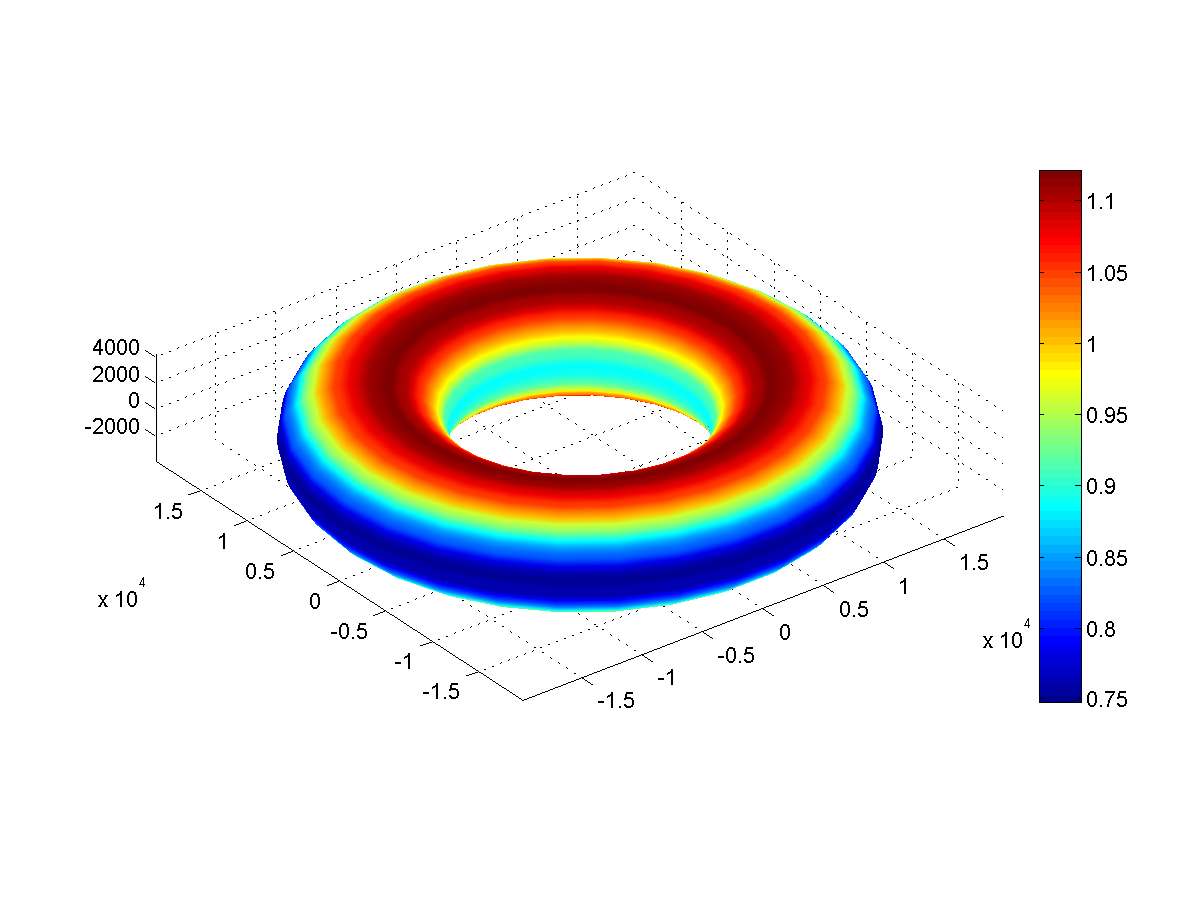
Рис. 4: поверхностная гравитация (м/с2) Обруча
У Обруча гравитация вдоль полюсов равна 1,1 G, а вдоль внешнего экватора – всего 0,75 G. На внутреннем экваторе она чуть побольше, порядка 0,81 G.
Скорость убегания – 19 км/с (вспомним, что планета весит в 6 раз больше Земли). На внешнем экваторе скорость убегания равна 9,9 км/с – ракете, запущенной на восток, нужно будет придать скорость в 10 км/с.
Ещё раз отмечу, что низкая гравитация на экваторе и высокая на полюсах не означает, что вещи будут скатываться или переползать к полюсам: как уже упоминалось, поверхность будет эквипотенциальной, поэтому гравитация совместно с центробежной коррекцией всегда будет к ней перпендикулярна.
Воздушные массы, текущие к полюсам, будут сплющиваться. Разница в гравитациях создаст горизонтальную разницу давлений, которая будет, действуя совместно с температурной разницей, создавать нетривиальные потоки.
Свет
Ночи и дни на таких мирах будут очень короткими. У окружающей среды не будет времени остыть или разогреться во время ежедневных циклов. Имеет значение разница в количестве света, получаемого во время более длинных периодов, то есть, сезонов. Если эти миры будут двигаться по орбите, схожей с земной, вокруг солнцеподобной звезды, это будет иметь значение.
Если орбита будет меньше, приливные силы довольно скоро сделают эти планеты нестабильными. Поскольку яркость звезды растёт примерно как четвёртая степень её массы, а радиус жилой зоны растёт, как квадратный корень яркости, то в жилой зоне масштаб приливных сил будет равен M/(√(M4))3=1/M5. То есть у ярких звёзд приливные эффекты будут куда как меньшими – возможно, Пончику и Обручу лучше вращаться вокруг бело-голубой звезды класса F, а не вокруг звезды класса G, как наше Солнце, просто на всякий случай.
Внешняя часть тороидальной планеты не слишком отличается от поверхности нормальной эллипсоидной. День настаёт, когда солнце встаёт над восточным горизонтом, а закат происходит над западным. Солнце проходит по большому кругу, медленно сдвигающемуся с севера на юг и обратно в течение года, что обеспечивает наличие сезонов. Однако на внутренней стороне планеты всё по-другому. Другие части планеты могут закрывать солнце – в первом приближении можно ожидать получения меньшей энергии.
Мы можем рассмотреть три различных случая: нулевой наклон оси, 23 градуса (как у Земли) и 45 градусов.
Нулевой наклон
При нулевом наклоне внутренняя сторона солнца не увидит: оно всегда будет спрятано за горизонтом или за мировой аркой. На полюсах солнце движется вдоль горизонта, а чуть ближе к центру всегда будут сумерки. Температурные различия будут большими, внутренняя часть планеты будет подвержена субарктическим температурам – это не сильно отличается от мира с синхронным вращением, и в принципе в этих местах вода (и, возможно, диоксид углерода) должны быть всегда сконденсированы. В результате на внешнем экваторе должны быть засушливые (возможно, не слишком жаркие места), возможно, обитаемые сумеречные околополюсные регионы, и заледенелая внутренняя часть.
Наклон в 23 градуса

Рис. 5: сезоны на Пончике весной, летом, осенью и зимой
Для наклона в 23 градуса, совпадающего с земным, весна и осень будут совпадать с нулевым наклоном – светло вдоль экватора и темно внутри, рядом с отверстием. Летом и зимой у солнца будет шанс проникать за обод, на противоположную сторону отверстия. Также будут существовать большие участки с солнцем в полночь или с вечной ночью летом или зимой. На Земле полярные регионы небольшие, но здесь они будут представлять собой длинные непрерывные круги.
Весенние рассветы и осенние сумерки на внутренней стороне должны давать удивительные глубокие цвета, поскольку солнце будет вставать сквозь атмосферу на другой стороне планеты (предварительно взошедшее или заходящее, если можно так выразиться). Всё это вместе с местными атмосферными оптическими эффектами даст очень глубокие красные цвета и градиенты. Сразу до или после заката или рассвета будут видны части солнечной короны.
Это зрелище было бы более впечатляющим, если бы не было таким коротким. На Земле солнце проходит порядка 15° в час. В самом быстром случае солнце проходит один свой диаметр за 2,1 мин. На Пончике солнце будет проходить 127° в час, а на Обруче — 102°. Восход и закат будут занимать 15 или 19 секунд соответственно. Наклонный угол и атмосферные задержки немного продлят зрелище, но для жителя земли оно будет слишком коротким.
Если вы будете стоять на внутренней стороне поверхности и смотреть вверх, то другая сторона будет занимать 20 градусов неба на Обруче и 30 градусов на Пончике – огромная арка через всё небо.
Почему Пончик не сильно шире? Он очень плоский, поэтому в небе выглядит укороченным. Это, кстати, значит, что при рефракции солнечного света через атмосферу другой стороны во время рассвета или заката красные цвета будут гораздо глубже, чем на Обруче.
Внутри освещённая противоположная часть тора будет освещать всё на манер лунного света. Но площадь поверхности будет больше, поэтому ночи будут гораздо ярче. На Обруче свет будет в 16000 раз сильнее Земного (8000 люкс), когда освещена вся противоположная часть (альбедо примем равным Земному), и ночь будет подобна облачному дню. На Пончике освещение будет достигать неяркого дневного (12000 люкс). Но это ситуация полностью освещённой противоположной стороны – во время равноденствия будет видна только тонкая полоска.
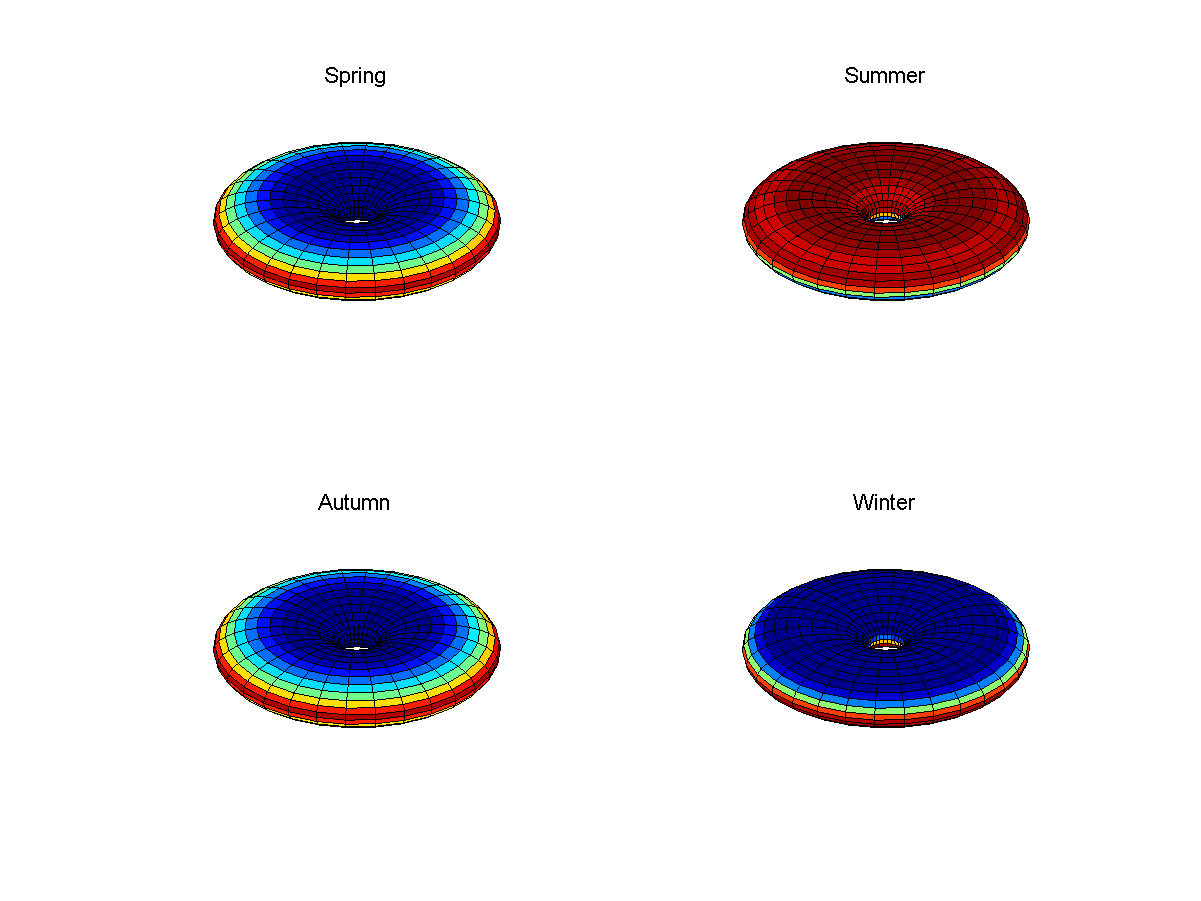
Рис. 6: средняя освещённость за день на Пончике во время весны, лета, осени и зимы для случая с уклоном в 23 градуса
В случае с Пончиком довольно плоская поверхность означает, что северное или южное полушарие (полуторие) получат много солнечного света. Общий разогрев планеты будет большим во время этих сезонов, чем во время весны и осени, в отличие от Земли, где он постоянный, поскольку остаётся постоянной получающая свет площадь. Также будут наблюдаться нетривиальные эффекты из-за углов между поверхностью и солнечным светом, и температурные зоны будут получать немного меньше энергии, чем полярные регионы и тропики.
На внешних тропиках будет примерно одинаковый приток солнечной энергии. По направлению к полюсам сезонность ощущается сильнее: тропики летом получают больше энергии, чем экватор в любое время. Зимы будут настолько же темнее. На полюсах и за ними, на внутренней стороне в местах с максимальной гравитацией солнце будет видно по полгода, а затем будет полярная ночь. Тут климат будет резко меняться – на внешних тропиках хотя бы будут ночи по 1,5 часа, а здесь они будут длиться по 6 месяцев. Наконец, ближе к внутреннему экватору рядом с отверстием, день и ночь будут равны зимой (и ещё добавится свет, отражённый другой стороной), поэтому температура будет чуть повыше.

Рис. 7: средняя освещённость во время разных сезонов на Пончике, как функция от широты в случае с 23 градусами. 0 обозначает внешний экватор, 90 – северный полюс, 180 – внутренний экватор, 270 – южный полюс.
Большое различие в объеме энергии, получаемой на солнечной летней стороне отверстия и на тёмной зимней стороне отверстия приведёт к появлению сильной непогоды – но из-за других странностей этих миров уравнять разницы энергий будет тяжелее, чем на Земле.
В среднем экваториальная внешняя часть будет получать в 2,5 раза больше энергии, чем полярные части, а внутренняя часть будет получать в четыре раза меньше энергии, чем прилегающие районы.
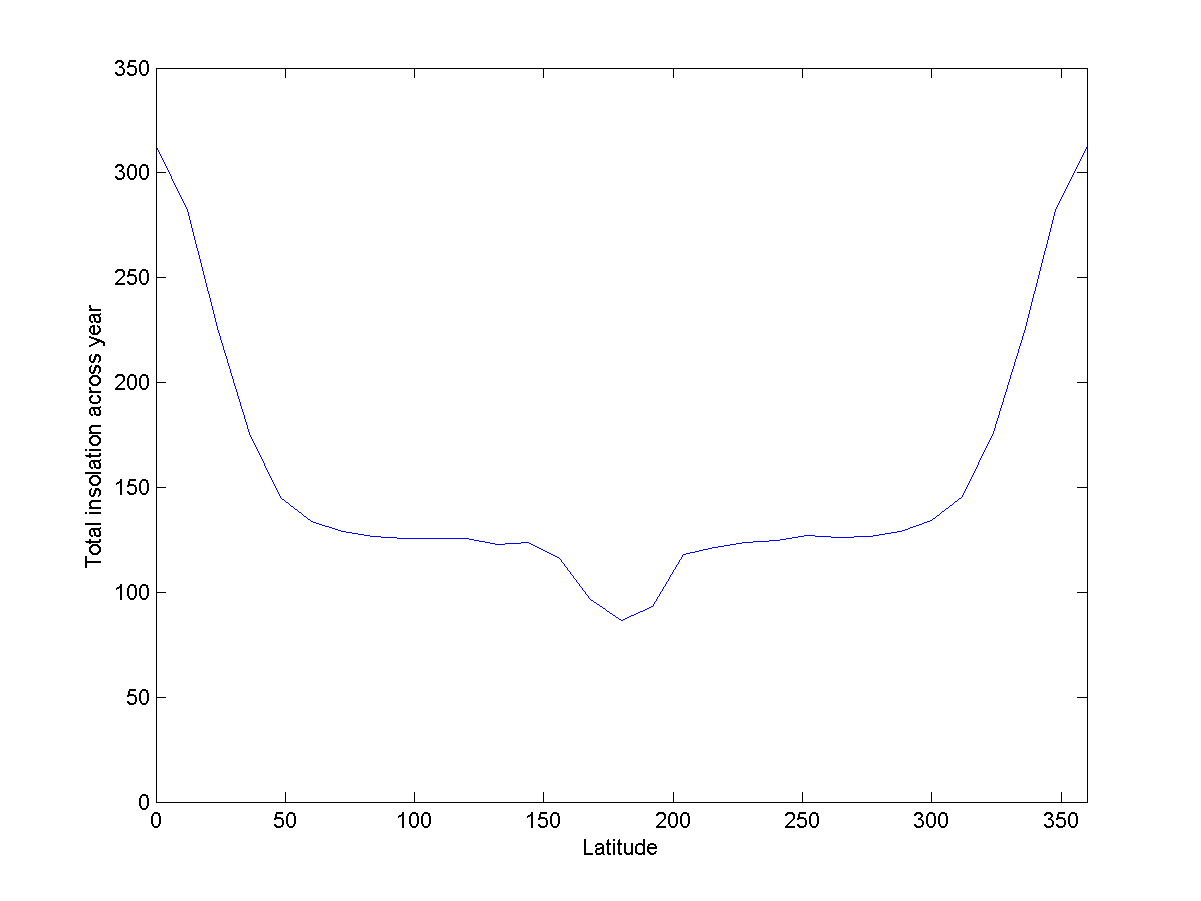
Рис. 8: энергия на разных широтах Пончика
Обруч отбрасывает на себя меньше тени. Что более важно, он не такой плоский, как Пончик.

Рис. 9: среднее освещение во время дня на Обруче, 23 градуса
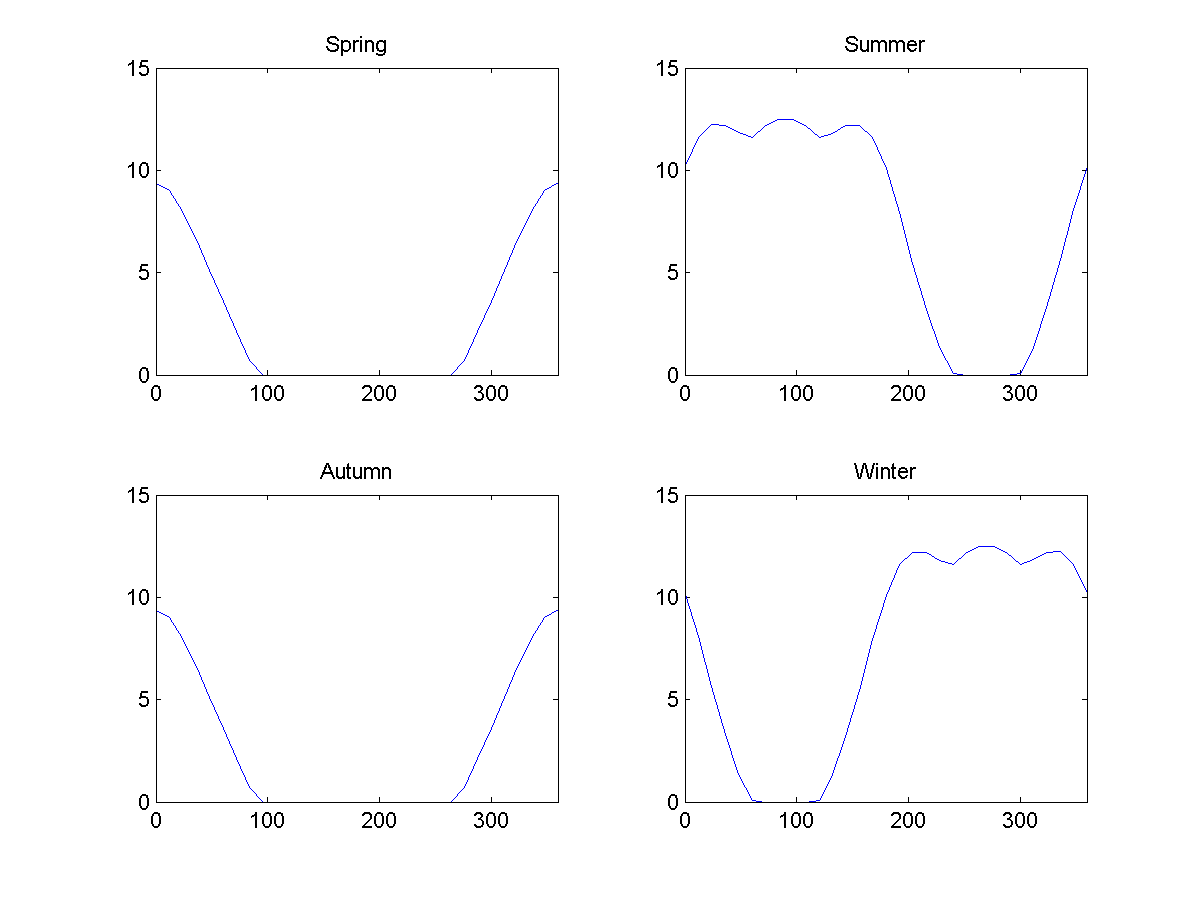
Рис. 10: среднее освещение во время разных сезонов на Обруче, как функция от широты в случае с 23 градусами. 0 обозначает внешний экватор, 90 – северный полюс, 180 – внутренний экватор, 270 – южный полюс.
На первый взгляд сезоны выглядят ожидаемо. Весной и осенью внутренние части будут скрыты в тени, летом и зимой один полярный регион освещён сильнее, а другой слабее, а внутренние части получат своё освещение. Это приведёт к наличию сезонного цикла во внутренней части планеты, идущего в два раза быстрее, чем на внешней (это будет так и на Пончике): тёплая погода будет в «июле» и в «январе».
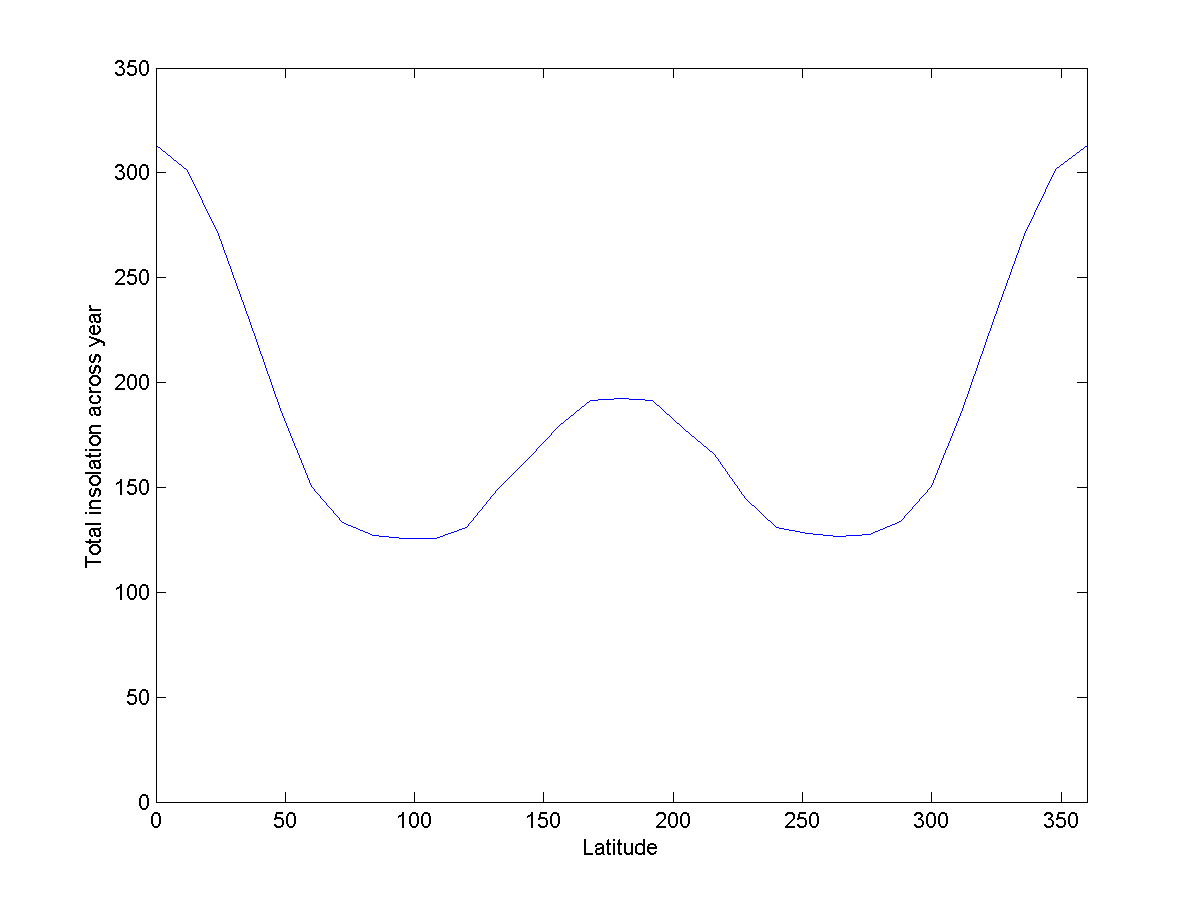
Рис. 11: получаемая в течение года энергия на разных широтах Обруча
По сравнению с Пончиком это будет неинтуитивно – внутренний экватор получает больше света в течение года, чем полярные области. Можно ожидать, что климат будет напоминать Земной – полярные регионы холоднее, экваториальные теплее. Но на внешнем экваторе солнца всё равно будет больше на 60%.
Наклон в 45 градусов
Возможно, самое удивительное открытие ждёт нас при наклоне на достаточно большой градус – оказывается, что в этом случае на планете появятся четыре холодных и четыре горячих зоны!
Проще всего представить это, подумав о сферической планете с осью, наклонённой на 90 градусов – такой, как Уран. Полгода северный полюс повёрнут к солнцу, и большая часть полушария постоянно освещена. С приближением равноденствия ось начинает смотреть вбок, и планета освещается равномерно. Конечный результат – полюса нагреваются больше экватора. На тороидальном мире будет происходить то же самое, но полярные регионы там будут круговыми.
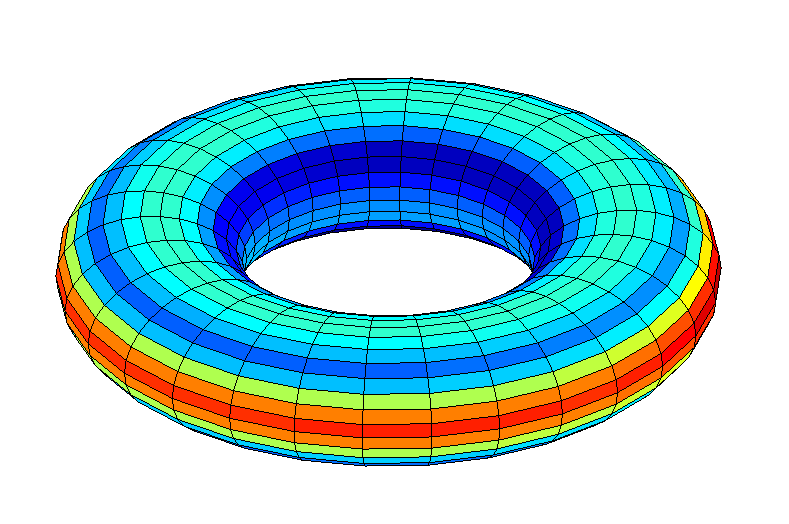
Рис. 12: энергия, получаемая в течение года на разных широтах Обруча в случае наклона 45 градусов
У Обруча разница будет не такой большой, порядка 10% общего освещения. Внешний экватор немного теплее полярных регионов и внутреннего экватора.
У Пончика разница побольше, но на практике на большей части поверхности преобладают средне тёплые полярные регионы. Внешний экватор лишь немного теплее соседних с ним температурных зон.
Геосфера
Площадь поверхности больше Земной, а отношение объёма к площади меньше (у пончика это 1300 км, у Обруча 1500 км, у Земли – 2124 км). В связи с этим можно ожидать, что наружу будет просачиваться больше термальной энергии, в результате чего вулканическая и тектоническая активности будут не такими сильными. Однако даже небольшое количество приливного разогрева из-за влияния солнца может освободить довольно много энергии углового момента. В случае Обруча внутри планеты будет в 6 раз больше радиоизотопов, чем на Земле, но лишь в 5 раз больше поверхности.
На дрейф континентов будет влиять разница внешнего и внутреннего радиусов. Круг, расположенный на r ближе к центру от круга радиуса R будет короче на 2 π r км, и относительное изменение будет выражаться через r/R. Поэтому на обруче континентальной плите, движушейся с внешнего экватора через полюс ко внутреннему, необходимо будет сжаться до 43% от первоначального размера. На Пончике эффект ещё больше – она сожмётся до 12% от размера! Поэтому континентальные плиты, двигающиеся к центру, будут складываться, а плиты, двигающиеся к окраине, будут раскалываться. Так что ближе к внутреннему экватору ландшафт будет очень пересечённый.
Гравитация влияет на высоту гор. Разница между Обручем и Землёй будет небольшой, но на Пончике горы на полюсах могут быть в 1,5 раза больше (до 12 км), а рядом с экваторами в 3 раза больше (24 км). Если учесть общую морщинистость поверхности рядом с дыркой, то ландшафт может быть весьма впечатляющим.
Быстрое вращение приведёт к появлению сильного магнитного поля. Но в отличие от Земли, тут в полярных регионах северного сияния не будет, поскольку линии полей не будут пересекать поверхность. Подсчёт динамо-токов тороида может быть интересным, но это не мой уровень.
Атмосфера
Мы обнаружили, что освещённость будет меняться гораздо быстрее, поэтому на планете должны быть довольно сильные ветра, передающие тепло от горячих освещённых областей в холодные и тёмные. Но быстрое вращение означает, что сила Кориолиса будет оказывать существенное влияние на ветра и течения.
Сила Кориолиса заставляет воздух, двигающийся к или от оси вращения, загибаться, поскольку его скорость отличается от скорости поверхности. Участок воздуха, «покоящийся» близ экватора, на самом деле обладает большим импульсом, поскольку экватор быстро движется вокруг оси вращения: если этот воздух потечёт к полюсу, у него будет заметная скорость, направленная на запад или восток. Поэтому общие воздушные потоки не ограничиваются простой конвекцией от экватора к полюсам: при передаче тепла воздухом он, двигаясь к полюсу, закручивается и рождает пассаты.
На тороидальных мирах скорость вращения в 8 раз превышает земную, и разницы в скоростях больше. Воздух закручивается гораздо сильнее, создавая более узкие климатические зоны, чем на Земле. Насколько они будут узкие, сказать трудно, не проводя детальных атмосферных подсчётов, но это больше будет похоже на Юпитер, чем на Землю. Это означает, что передача тепла будет менее эффективной – температурные различия между горячими и холодными областями будут больше.
Скорее всего, там будет существовать внутритропическая зона конвергенции (Intertropical Convergence Zone, ITCZ) вокруг внешнего экватора, где ветра, сходящиеся с севера и юга, будут дуть на запад (пассаты), а тёплый воздух будет подниматься, двигаться по направлению от экватора, охлаждаться и спускаться на высоких или низких широтах (где должны существовать большие пустыни). Ощутимая сезонность, особенно на Пончике, сдвинет ITCZ на север и юг, что в некоторых регионах приведёт к появлению муссонов. Однако быстрое вращение сделает ячейку Хэдли тоньше, чем 30 градусов на Земле (насколько тоньше, довольно сложно оценить, поскольку это ещё зависит от меняющейся от широты гравитации).
Большое изменение температур на коротких расстояниях говорит о наличии жёстких погодных условий, хотя довольно сложно понять, какими именно они будут. Особенно ближе к дырке на Пончике сезонная погода будет очень дикой: тёплый воздух с освещённой стороны будет течь через неё, закручиваясь в большую воронку, и его будет балансировать холодный ветер с тёмной стороны, циркулирующий в противоположном направлении.
Высотные масштабы, падение давления с высотой, пропорционально гравитации. Поэтому на Пончике облака будут в 1,5-3 раза выше, чем земные, а на Обруче не будут особенно отличаться от земных.
Как и на Земле, на средних широтах смогут образовываться циклоны. Большее влияние силы Кориолиса приведёт к появлению более плотных ураганов – примерно в четыре раза меньше. Однако на Пончике они будут длиться дольше (поскольку большая шкала высоты даёт им больше воздуха для развития). Скорости ветра зависят от температурных различий между поверхностью океана и верхней частью атмосферы, которые в течение года могут сильно меняться.
Гидросфера
Количество воды на обоих мирах не сильно отличается от земного, хотя на Обруче, с массой в 6 раз больше, площадь будет всего в 5 раз больше, поэтому объём воды на нём будет на 20% больше из-за изначальной аккреции (поэтому при той же площади океаны будут глубже на 20%). Увеличенная масса может привлекать больше комет, но сложно оценить, насколько именно.
Большие сезонные колебания температуры будут более выражены дальше от океанов: континенты у полюсов будут обладать более экстремальной погодой, чем на экваторе. Их способность поддерживать полярные шапки во время полярного лета зависит от их конфигурации и фоновой температуры; поскольку лёд эффективно отражает солнечные лучи, а сила Кориолиса может удерживать эти области от разогрева, то наличие таких шапок вполне вероятно. То же можно сказать и о морском льде, хотя тут могут появляться тёплые морские течения. Поскольку течение воды в океане ограничивается формой бассейна, сила Кориолиса просто будет обеспечивать круговое вращение, и не будет предотвращать потоки с севера на юг. Большие океаны, типа Тихого, будут больше растянуты с запада на восток.
Низкая гравитация рядом с экватором приведёт к появлению высоких волн на Пончике: можно ожидать, что они будут в три раза больше земных. На полюсах Пончика волны будут достигать 150% от земных. Обруч будет ближе к привычным волнам (133% на экваторе, 90% на полюсах). Плохая погода в период лета и зимы ближе к центру Пончика приведёт к появлению гигантских штормовых волн.
Биосфера
Исходя из этих соображений можно представить наличие на Пончике и Обруче биосферы, довольно похожей на земную. На Земле существа неплохо адаптировались к штормам, плохой погоде, длинным зимам. Экосистемы могут интересным образом меняться в зависимости от широты, поскольку различий между поясами там больше, чем на Земле (гравитация, сезонность, температуры). Также, по крайней мере на Обруче, у каждого пояса будет гораздо больше площадь – больше места для разнообразия видов в каждой экологической нише.
Луны
Смогут ли эти миры удерживать луны?
Луна, обращающаяся в плоскости экватора по круговой орбите около тороида, не будет ощущать отличий от круглой планеты. Однако при приобретении эксцентричности всё будет усложняться. Потенциальное поле при приближении к планете падает медленнее, чем 1/r, как у нормальных планет: эллипс Кеплера уже не подойдёт в качестве решения. С наклоном орбиты система становится ещё более сложной – теперь луна будет чувствовать уплощённость планеты.
В каком-то смысле с похожей проблемой уже сталкиваются разработчики спутников: Земля достаточно сплющена у полюсов, чтобы это было заметно. Эту проблему решали на ранних стадиях космических полётов (Wikipedia, (Tremaine & Yavetz 2013) or (Nielsen, Goodwin,& Mersman 1958)).
По сути, эллиптическая орбита подвержена прецессии – постепенно меняет направление, и в случае с Землёй это зависит от наклона орбиты. Эксцентричность тоже может плавать. В любом случае для тороида эти эффекты будут выражены ярче. Они будут настолько сильными, что стандартные методы расчётов уже не работают, и нам придётся проводить компьютерные симуляции.
Уверен, что луны на достаточно удалённых круговых орбитах будут вести себя достаточно стабильно. Скорее всего, они будут подвержены прецессии, поэтому их орбита будет больше похожа на розетку, чем на эллипс, но с катушек слетать они не будут. Конечно, если орбита луны ближе, всё будет по-другому.
В симуляции (я использовал не полный тор, а кольцо из 30 масс) мне открылось несколько возможностей. Экваториальная эллиптическая орбита выглядит аккуратной и стабильной, но прецессия превращает её в розетку.
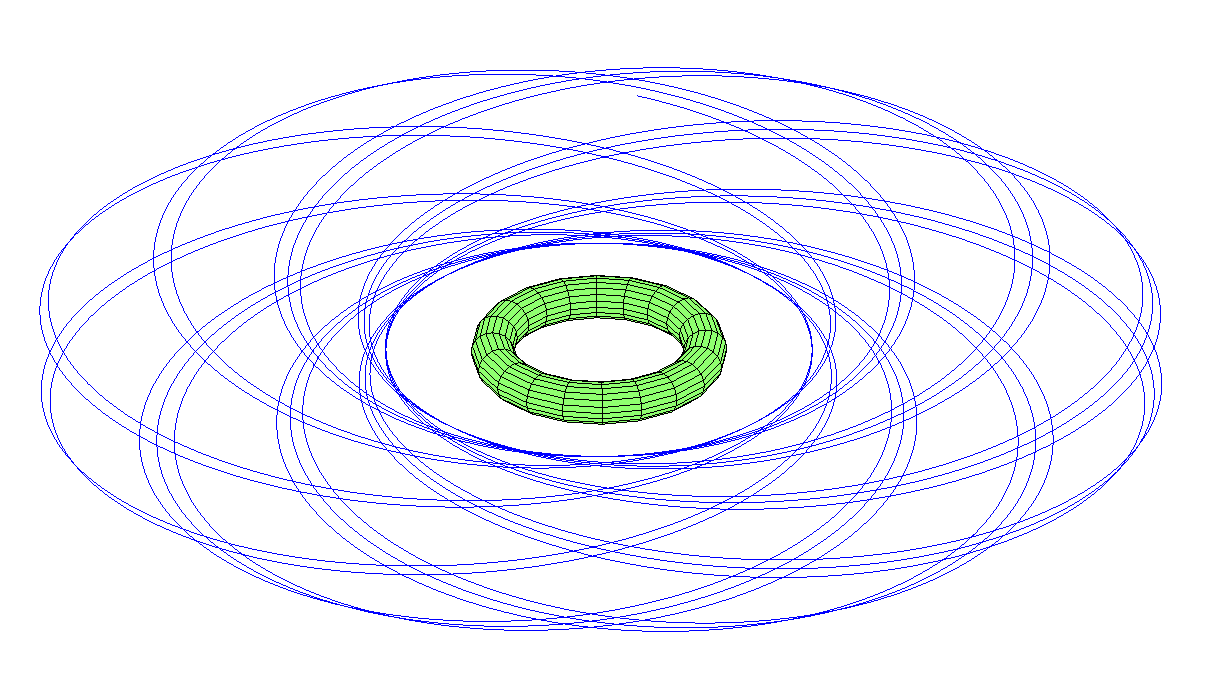
Околополярная орбита прецессирует ещё больше, появляется не только розетка, но и прецессия плоскости. Луна на небе может появиться в любом созвездии.
Что насчёт орбит, проходящих через дырку? Как я уже отмечал ранее, геометрический центр – нестабильная точка Лагранжа. Если там расположить луну, то любой удар выбьет её оттуда. Но существуют стабильно выглядящие орбиты через центр (точнее, при любом воздействии они превратятся в другую похожую по форме орбиту). Простейший вариант – луна, болтающаяся туда и сюда через дырку, как маятник:
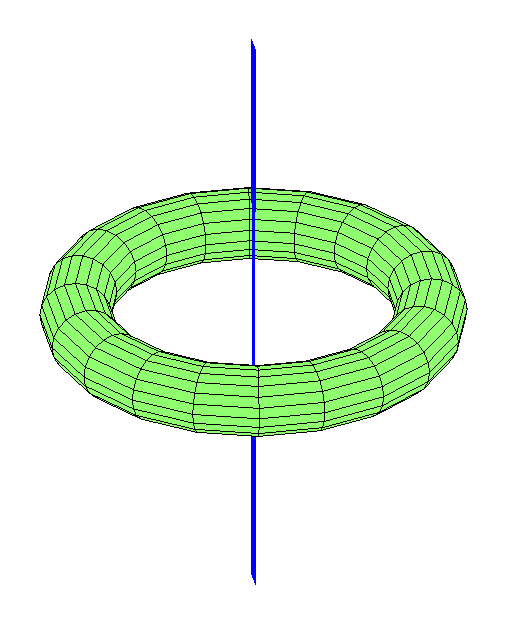
Можно представить луну, пролетающую на определённой долготе:
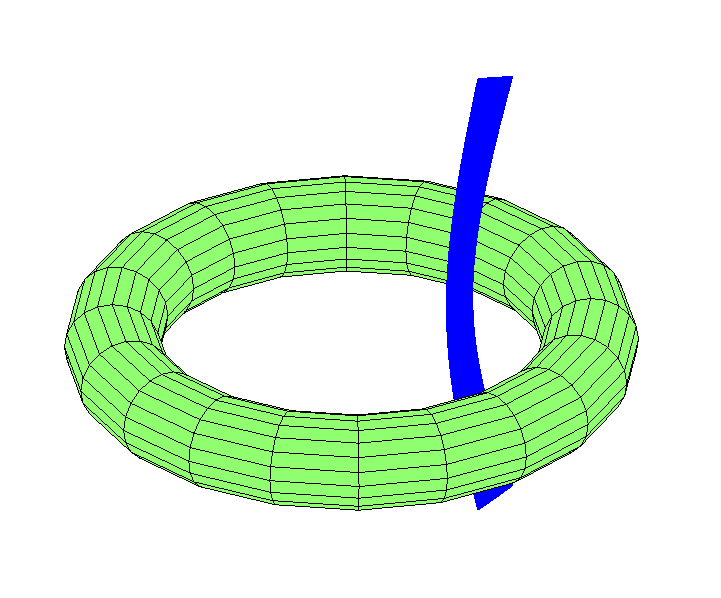
С приобретением скорости по долготе она будет перемещаться в дырке:

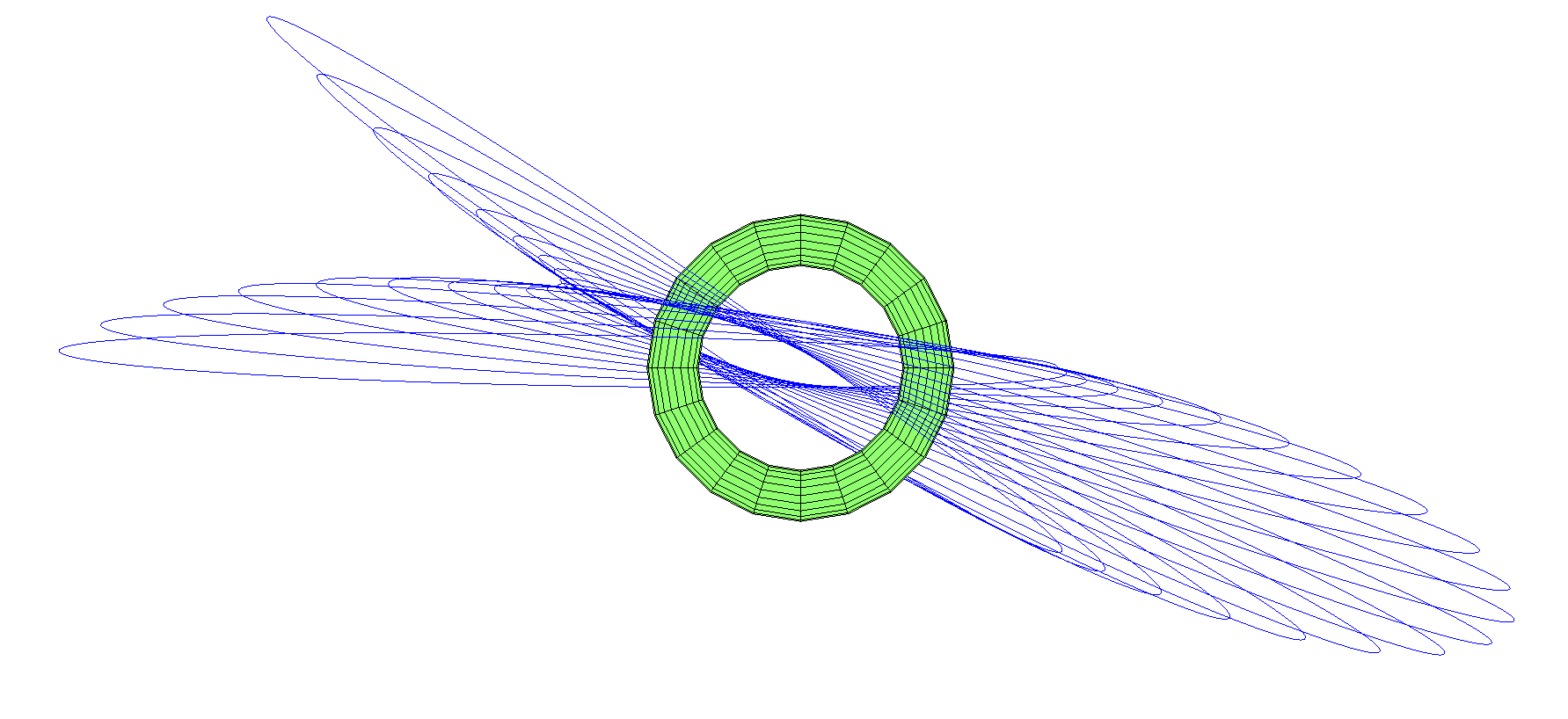
Что насчёт траекторий, проходящих через дырку в одном направлении? Оказалось, существует довольно много орбит-восьмёрок, рисующих большой тороидальный клубок.

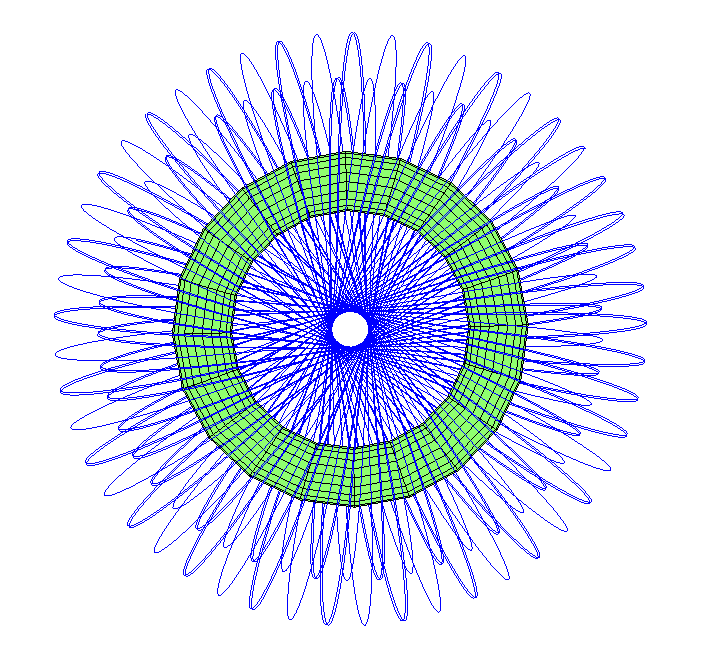
Обратите внимание, что орбита немного вытянута. С «апогея», над внешним экватором, она проходит через дырку, появляется на обратной стороне, где испытывает перигей в точке, противоположной начальной. Затем она вновь проходит через дырку, и выходит рядом с тем местом, где начала движение – но прецессия закручивает её по тору.
Эти симуляции стоит воспринимать как первичные черновики – реальные вычисления требуют большей точностью. Моей численной точности не хватает для того, чтобы оценить долговременную стабильность. Гравитационные поля Пончика и Обруча выглядят ещё сложнее из-за их сплющенности, а ещё свой вклад будут вносить солнце и другие планеты.
Приливные силы
Приливные силы – это проблема. Представьте себе луну, движущуюся вокруг тороида. За ней образуются вздутие воды и камня. Быстрое вращение будет толкать вздутие вперёд луны (если луна движется в направлении вращения планеты и находится над геостационарной орбитой). Притяжение вздутия будет само тащить луну вперёд, придавая ей ускорение – и в космосе это заставляет луне двигаться по более высокой орбите. Именно так Луна переняла достаточно много углового момента Земли, замедлила её вращение и отдалилась от неё. В случае быстрого вращения, как у наших тороидов, эффект будет заметнее: луны будут улетать от планеты и, вероятно, теряться.
Что будет с лунами, находящимися близко, ниже геостационарной орбиты? Они будут двигаться быстрее вздутия, которое будет их замедлять. Орбита будет понижаться. Вскоре они по спирали опустятся вниз и превратятся в гигантские метеоры. То же случится с лунами, движущимися в противоположном направлении. Конечно, если луна будет достаточно большой, приливные силы могут разорвать её и превратить в кольцо.
Более широкие орбиты, проходящие через дырку, скорее всего, будут терять стабильность. Орбиты-маятники будут приобретать угловой момент из-за вздутия, и луна будет двигаться быстрее и быстрее, пока не улетит от планеты, или не упадёт. Некоторые орбиты-восьмёрки могут войти в резонанс и в равных долях приобретать и терять энергию, но их будет подстерегать сходная проблема. Так что, скорее всего, у тороидов не будет по-настоящему экзотических лун. Однако никто не запрещает запускать искусственные спутники с поддержкой орбит. Орбиты-маятники могут пригодиться спутникам связи на внутренней поверхности тора.
Итог
Тороидальные миры вряд ли появятся естественным образом. Но если появятся, это будут удивительные места для поиска приключений. Большая площадь поверхности. Регионы с сильно отличающимся климатом, сезонами, гравитацией и экосистемами. Удивительное небо на внутренней стороне. Необузданная погода. Луны на странных орбитах.
Хорошо бы научиться создавать их не только в симуляциях.
Андерс Сандберг — исследователь, участник научных дебатов, футуролог, трансгуманист и писатель. Он получил степень доктора философии в вычислительной нейробиологии в Стокгольмском университете, и в настоящее время является научным сотрудником Исследовательского общества Джеймса Мартина в Институте будущего человечества при Оксфордском университете.
Автор: Вячеслав Голованов






