Вычислительные методы в оптике или как моделировать электромагнитные процессы на различных пространственных масштабах

Среди численных методов, используемых в процессе проектирования современных оптических компонентов, обычно выделяют две большие группы: универсальные полноволновые и приближенные. Выбор конкретного подхода зависит от соотношения моделируемого объекта с длиной волны и характера распространения электромагнитных волн.

Полноволновые методы, основанные на непосредственном решении волновых уравнений для компонент электромагнитного поля при заданных граничных условиях, обычно применяются для разработки оптических микро- и наноустройств. В то время как для проектирования макроскопических систем типа фокусирующих линз, интерферометров и монохроматоров используются приближенные методы. К ним, в частности, можно отнести геометрическую трассировку лучей.

В данной заметке помимо краткого разбора двух традиционных методов, мы расскажем о более новом подходе, который получил название "метод огибающей пучка" (beam envelope method), и обсудим его преимущества для задач вычислительной оптики.

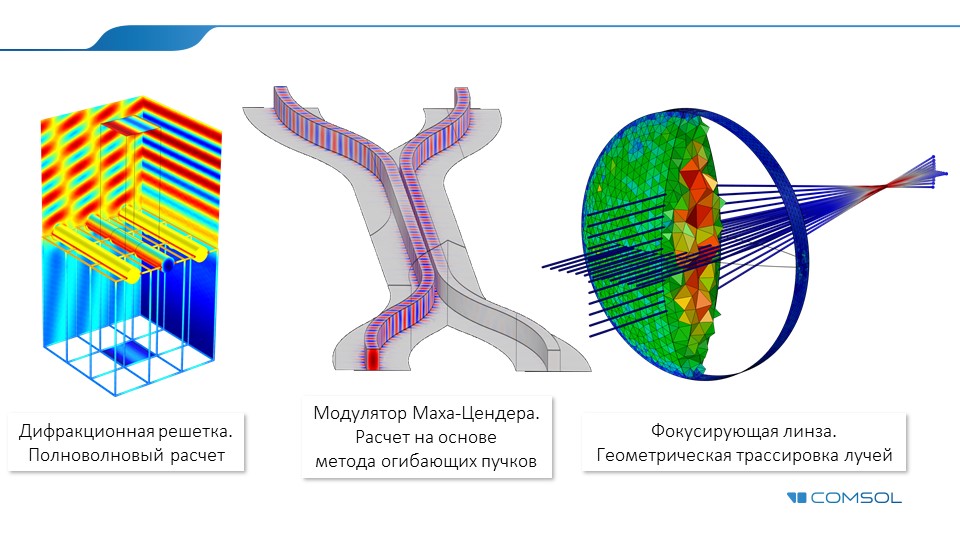
Полноволновые методы

К первой группе относят спектральный метод, метод моментов, метод конечных разностей и метод конечных элементов. Они успешно использовались на протяжении многих лет и активно продолжают применяться в настоящее время в анализе таких важных оптических компонентов, как оптоволоконные структуры, направленные ответвители, кольцевые резонаторы и т.п. С помощью перечисленных методов инженеры и исследователи могут проводить точный анализ распространения волн в оптических структурах, используя минимальный набор физических допущений. Последние связаны с дискретизацией при преобразовании кусочно-непрерывной оптической среды в цифровую (дискретную) модель. Таким образом, явления дифракции, интерференции и резонансные моды низкого порядка можно отследить с практически произвольной точностью, просто увеличивая уровень дискретизации (рис. 1), при этом сами такие методы обычно называют полноволновыми (full-wave).

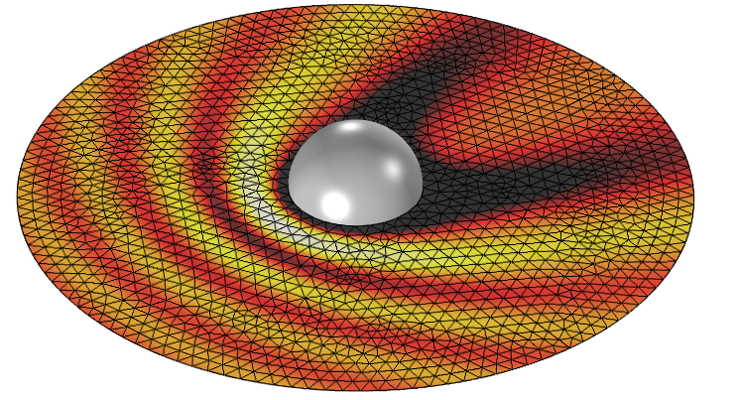
Рис.1. Падение плоской электромагнитной волны на золотой наносфере: картина рассеянного э/м поля и расчетная конечно-элементная сетка.

В общих чертах, для конечно-разностных методов увеличение уровня дискретизации сводится к добавлению дополнительных точек в расчётную область и получению более гладкого представления электромагнитного поля. Аналогичный принцип применим и к другим методам. Однако большее число точек дискретизации приводит к увеличению требуемых для расчета вычислительных ресурсов. Для 3D-моделей число таких точек пропорционально длине волны в кубе. Согласно критерию Найквиста, на длину волны должно приходиться не меньше двух точек дискретизации по каждой оси координат, а в реальных условиях — даже больше (обычно не менее 5 элементов второго порядка в каждом пространственном направлении). На практике вычислительные затраты растут еще быстрее, поэтому для расчета объектов, в размеры которых укладывается большое количество длин волны (более 50), полноволновые методы используются редко при отсутствии прочих альтернатив.

Простой пример: ширина оптического волокна может составлять лишь несколько длин волны, а его длина — несколько миллиардов длин волн. Для анализа мод, распространяющихся в поперечном сечении волокна, полноволновые методы отлично подойдут, поскольку относительный размер волокна в этом направлении небольшой (рис. 2). Напротив, для анализа распространения волн вдоль волокна и возможных дефектов волокна приходится прибегать к приблизительным методам, чтобы не исчерпать оперативную память компьютера.

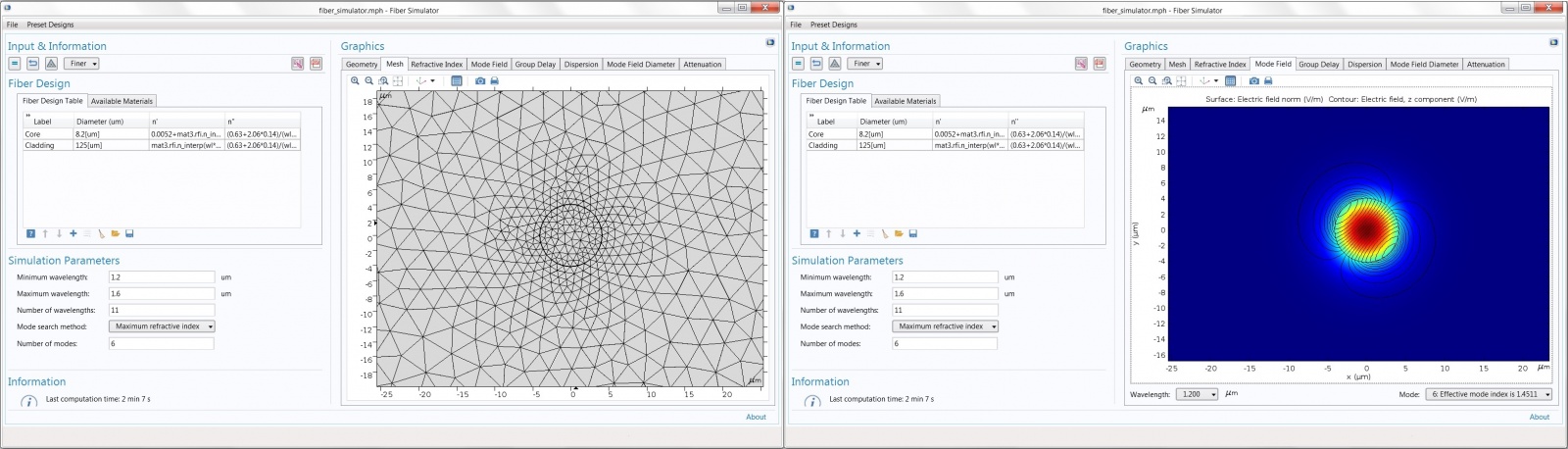
Рис. 2. Расчет на основе метода конечных элементов оптоволоконной структуры: конечно-элементная сетка (слева) и одна из поперечных мод волокна на длине волны 1,2 мкм (справа).

Приближенные методы

Приближенные методы подразумевают использование некоторых изначальных упрощений или приближений. К этому классу методов относятся такие методы, как трассировка лучей (или геометрическая оптика), гауссова оптика и метод распространения пучка (beam propagation method — BPM). В отличии от полноволнового подхода, при выполнении определенных условий, приближенные методы могут применяться к решению задач на гораздо более крупных объектах.

Например, в линзе диаметром 1 см в любом направлении укладываются десятки тысяч длин волн видимого света. В этом случае, лучше всего себя показывает метод трассировки оптических лучей. Расплатой за приближение является отказ от учета некоторых физических явлений: в геометрической оптике обычно пренебрегают дифракцией — лучи распространяются по прямым линиям (рис. 3).

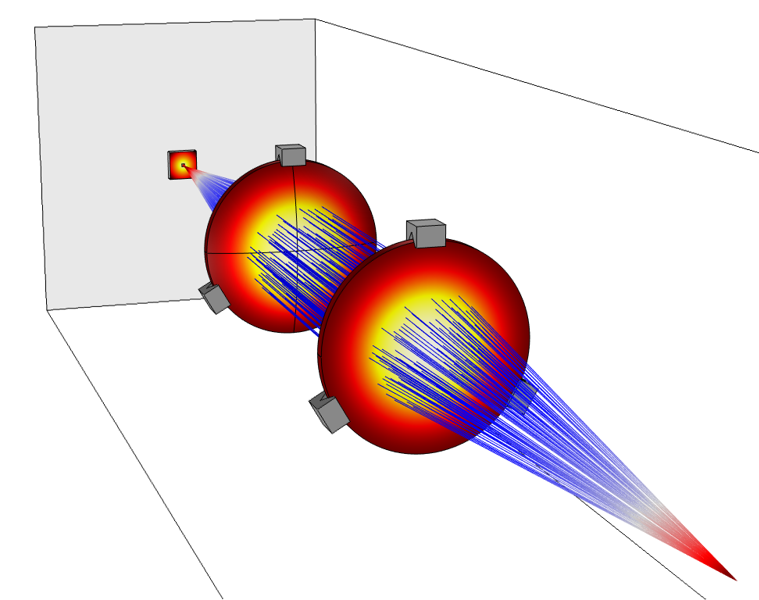
Рис. 3. Численный анализ распространения электромагнитных волн в системе фокусировки лазерного пучка обычно основан на трассировке лучей, а не на непосредственном решении уравнений Максвелла полноволновым методом.

Метод огибающей пучка

Волноводы в оптических системах обычно имеют одно предпочтительное направление распространения волн. На языке математической физики это означает, что существует определенный волновой вектор, слабо меняющийся или даже остающийся постоянным в направлении распространения. На этом основан новый вычислительный метод — метод огибающей пучка (beam envelope method).

В самом общем случае электрическое поле распространяющейся волны содержит три компоненты: . Предположим, что ось z является предпочтительным направлением распространения, а поле внутри волноводной структуры значительно осциллирует вдоль оси z и содержит намного более медленные изменения в направлениях x и y. Тогда, поле непрерывной электромагнитной волны с постоянной частотой можно представить в виде , где — угловая частота, — константа распространения по оси z, а — медленно меняющаяся амплитуда.

Это выражение в комплексной форме можно подставить в полный набор уравнений Максвелла и, используя ряд классических алгебраических преобразований, добиться сокращения всех быстро изменяющимся множителей , получив итоговое уравнение относительно медленно изменяющейся огибающей поля . Именно на этом удачном сокращении быстропеременной составляющей и основан метод огибающей пучка. Чтобы вернуться к истинному выражению для электромагнитной волны, следует лишь умножить полученное выражение на этот множитель.

В слу отсутствия приближений (единственное допущение касается известного изначально направления распространения волны), данный подход может быть классифицирован как полноволновый метод (рис. 4), но при этом он обладает одним важным преимуществом. Проблема полноволновых методов в том, что они требуют достаточного количества расчетных точек или узлов в выборке, т.к. противном случае результаты вычислений окажутся просто числовым "мусором". Для решения уравнения относительно медленно изменяющейся огибающей поля достаточно гораздо меньшего числа узловых точек (при сохранении справедливости критерия Найквиста), по крайней мере, в тех случаях, когда в задаче есть явно выделенное направление распространения, как, например, в оптических волноводах (рис. 4). Таким образом, необходимое число точек или узлов дискретизации может быть снижено на порядок (в некоторых случаях даже больше). Важно отметить, что для расчета огибающей пучка можно использовать любой универсальный метод, в частности МКЭ, а затем для получения полного решения достаточно просто умножить огибающую на известную (изначально заданную) быстро изменяющуюся составляющую.

Данный подход существенно отличается от схожего по названию метода — метода распространения пучка, который использует дополнительные упрощения и приближения, пренебрегая некоторыми производными в волновом уравнении.

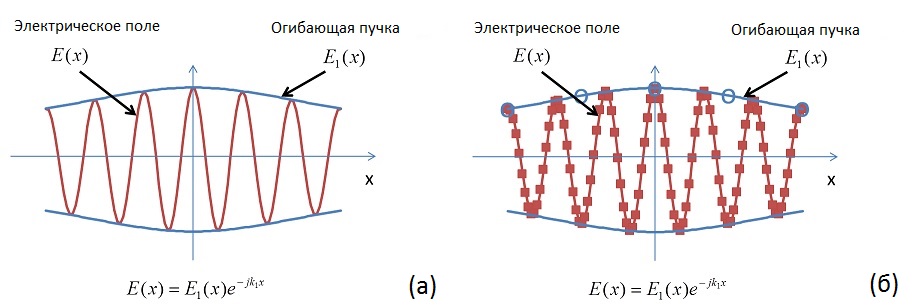
Рис. 4. Сравнение дискретизации традиционного полноволнового метода и метода огибающей пучка.

Метод огибающей пучка и направление распространения волны

Возможность расчета длинных и тонких конструкций с более или менее постоянным направлением распространения волн очень полезна, и применить к таким случаям метод огибающей пучка довольно просто. Тем не менее, многие волноводные структуры изогнуты в одном или нескольких направлениях. Предложенный метод будет работать и в этом случае, но при этом есть некоторые ограничения, связанные с геометрической сложностью конструкции. Если вектор распространения медленно меняет свое направление, метод остается справедливым. Чтобы понять, что происходит в этом случае, вернемся к полному выражению для электромагнитного поля , где направление распространения изначально задано по оси z. Для обобщения этого выражения на случай произвольного направления, запишем его в виде , где — вектор, определяющий предпочтительное направление распространения волны, а — вектор координат, — их скалярное произведение.

На практике последнее обычно задают равным пространственно-распределенной фазовой функции . Тогда с точки зрения метода огибающей пучка условие медленного изменяющегося направления распространения заменяется на условие медленно меняющейся фазы. Например, кольцевая часть резонатора радиуса R может быть описана фазовой функцией , где — константа распространения, соответствующая длине волны в направлении распространения (рис. 6).

Рис. 6. Анализ кольцевого резонатора на длине волны 1,559 мкм. Слева показана конечно-элементная сетка, в центре — физическое быстропеременное поле, а справа — медленно меняющаяся огибающая поля, расчитанная с помощью метода огибающей пучка.

Таким образом, метод огибающей пучка можно применять к оптическим конструкциям, составленным из простых форм, где каждый составной компонент можно описать через функцию , соответствующую предпочтительному локальному направлению распространения. Например, кольцевой резонатор, содержащий одну прямую секцию и одну кольцевую секцию, можно исследовать, используя одну постоянную и одну "круговую" фазовые функции. В более общем случае фазовая функция может задаваться как интерполяция некой простой зависимости от координатного вектора. Кроме того, пользуясь принципом суперпозиции полей, можно анализировать два (прямая и обратная волна) и более направления распространения (включая задачи с отражением и преломлением), записывая несколько наборов фазовых функций (рис. 7).

Рис. 7. Распределение медленно меняющейся огибающей поля в симметричном лазерном резонаторе. В расчете используется суперпозиция волн (прямой и обратной), распространяющихся в двух направлениях.

Применение метода огибающей пучка в нелинейной оптике

Нелинейные оптические эффекты зачастую достаточно слабы и возникают на больших длинах взаимодействия, а именно в таких случаях метод огибающей пучка является наиболее подходящим. Один из примеров нелинейных эффектов — самофокусировка. Этот явление можно наблюдать в лазерных стержнях или оптических стеклах, находящихся в точке фокуса (например, Nd:YAG — алюмо-иттриевом гранате, легированном неодимом). Знание пороговых значений самофокусировки на стадии проектирования позволит избежать повреждения материалов, используемых в конструкции различных элементов (рис. 8).

Рис. 8. Численное исследование самофокусировки в стержке из BK-7 длиной 20 см, т.е. порядка 300 тысяч (!!!) длин волн. Изображение справа — истинное соотношение сторон, слева — промасштабированная визуализация нормы и z-компоненты огибающей поля.

Метод применим и для других нелинейных эффектов: генерации второй гармоники, генерации суммарной и разностной частоты, параметрической генерации и усиления, а также фазовой автомодуляции.

Заключение

Метод огибающей пучка позволяет значительно увеличить размеры моделей, к которым применимы полноволновые методы. Он заполняет пробел между требовательными к вычислительным ресурсам, но точными конечно-разностными и конечно-элементными схемами и быстрыми приемами трассировки лучей. Подход применим для реальных задач проектирования, что подтверждает успешное решение прикладных задач, как из области нелинейной оптики, так и междисциплинарных постановок, например по расчету модуляторов Маха-Цендера.

Разработчики метода и его реализации в COMSOL ожидают, что его сочетание с традиционными полноволновыми и приближенными методами откроет новые горизонты в оптике и вычислительной электродинамике для комплексного исследования э/м процессов на различных пространственных масштабах.

P.S. Дополнительная информация

Данная статья основана на материалах журнала Optik & Photonik.

Для более подробного знакомства с описанными методиками приглашаем поучаствовать в нашем новом вебинаре "Полноволновые расчеты протяженных оптических компонентов в COMSOL Multiphysics^®", который состоится 29 ноября 2017 года.

Автор: Сергей Янкин

Источник