Уравнение Пуассона и распределение Больцмана (часть 2.1)

2017-09-22 в 6:18, admin, рубрики: статистическая физика, физика

Распределение Больцмана (часть 1)

Прежде чем подойти к выводу распределения Больцмана и разобраться в физическом смысле, необходимо дать предварительные сведения по элементарной теории вероятностей. Дело в том, что макросистемы, которые мы наблюдаем, состоят, как известно, из огромного числа более мелких частиц, например, любое вещество состоит из атомов, а последние в свою очередь делятся на ядра и электроны, ядро атома разбивается на протоны и нейтроны и так далее. В материальной системе, имеющей огромнейшее число частиц (в так называемой микросистеме) бессмысленно рассматривать каждую частицу в отдельности, во-первых потому что никто никогда не сможет описать каждую частицу (даже современные суперкомпьютеры), во-вторых это ничего нам не даст в принципе, потому что поведение макросистемы описывается усреднёнными параметрами, как мы увидим дальше. При таком огромном количестве частиц есть смысл интересоваться вероятностями того, что какой-то параметр лежит в том или ином диапазоне значений.

Итак, приступим к некоторым определениям из теории вероятностей, а затем, объяснив обязательно распределение Максвелла, подойдём к разбору распределения Больцмана.

В теории вероятности есть такое понятие как случайное событие – это явление, которое в некотором опыте либо имеет место быть, либо нет. Например, рассмотрим замкнутый ящик, в котором находится молекула А и некоторый выделенный объём $Delta tau$ в этом ящике (см. рис. 1).

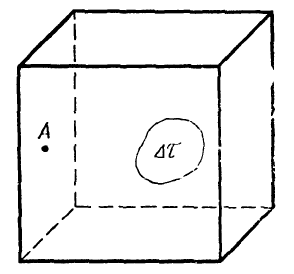
Рис. 1

Так вот, случайное событие будет либо попадание молекулы А в выделенный объём $Delta tau$ , либо отсутствие этой молекулы в этом объёме (ведь молекула двигается, и в любой момент времени она либо есть в некотором объёме, либо нету).

Под вероятностью некоторого случайного события понимают отношение числа испытаний m, при котором данное событие имело место, к полному числу испытаний M, причём полное число испытаний должно быть велико. Мы не можем говорить о вероятности какого-то события при одном испытании. Чем больше испытаний, тем точнее вероятность события.

В нашем случае вероятность того, что молекула А будет находится в объёме $Delta tau$ равна:

$W(A)=frac{m}{M} , или W(A)=lim_{Mto infty} m/M$

Рассмотрим теперь в том же самом ящике два выделенных объёма $Delta tau_1$ и $Delta tau_2$ (см. рис. 2)

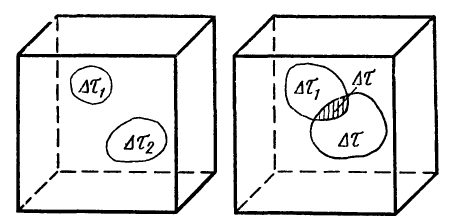
Рис.2

Если эти два объёма не пересекаются (см. рис. 2а), то молекула А может в какой-то момент времени t находится либо в объёме $Delta tau_1$ , либо в объёме $Delta tau_2$ . Одновременно одна молекула не может находится в двух разных местах. Таким образом, мы подошли к понятию несовместимых событий, когда реализация одного события исключает реализацию другого события. В случае, когда объёмы $Delta tau_1$ и $Delta tau_2$ пересекаются (см.рис.2б), то есть вероятность, что молекула может попасть в область пересечения, и тогда два события являются совместимыми.

Вероятность того, что молекула А попадёт в объём $Delta tau_1$ равна:

$W(1)=m_1/M$

, где $m_1$ – число испытаний, когда молекула была в объёме $Delta tau_1$ . Точно также, вероятность того, что молекула А попадёт в объём $Delta tau_2$ равна:

$W(2)=m_2/M$

Далее, событие, состоящее в том, что молекула попадёт хотя бы в один из двух объёмов, осуществилось $m_1 + m_2$ раз. Отсюда вероятность этого события равна:

$W=frac{m_1 + m_2}{M}=frac{m_1}{M} + frac{m_2}{M}=W(1) + W(2)$

Таким образом, мы может заключить, что вероятность осуществления одного из несовместимых событий равна сумме вероятностей осуществления каждого из них.

Полной группой несовместимых событий называется такая совокупность событий, в которой осуществление одного достоверно, т.е. вероятность одного из событий равна 1.

События называются равновозможными, если вероятность осуществления одного из них имеет одно и то же значение, т.е. вероятности всех событий одинаковые.

Рассмотрим последний пример и введём понятие независимых событий. Пусть первое событие заключается в том, что молекула А в момент времени t находится в объёме $Delta tau_1$ , а второе событие – что другая молекула B попадает в объём $Delta tau_2$ . Если величина вероятности того, что молекула B попадёт в объём не зависит от того, попала молекула А в $Delta tau_1$ или нет, то эти события называются независимыми.

Пусть мы выполнили всего n испытаний, и выяснили что молекула А была $m_1$ раз в объёме $Delta tau_1$ , а молекула B — $m_2$ раз в объёме $Delta tau_2$ , то вероятности этих событий равны:

$W(A)=frac{m_1}{n}, W(B)=frac{m_2}{n}$

Отберём из испытаний $m_1$ , при которых A попала в $Delta tau_1$ число испытаний, при которых ещё и B попала в $Delta tau_2$ . Очевидно, что это число отобранных испытаний равно $m_1(frac{m_2}{n})$ . Отсюда вероятность совместного осуществления событий А и B равна:

$W(AB)=frac{m_1(frac{m_2}{n})}{n}=frac{m_1}{n} frac{m_2}{n}=W(A) W(B)$

Т.е. вероятность независимых событий при совместном осуществлении равна произведению вероятностей каждого события в отдельности.

Если мы измеряем некоторую величину, например скорость молекулы, или энергию отдельно взятой молекулы, то значение может принимать любое вещественное значение на числовой оси (в том числе и отрицательные значения), т.е. эта величина является непрерывной, в отличие от того, что мы рассматривали выше (так называемые дискретные величины). Такие величины называют случайные величины. Для непрерывной случайной величины неверно интересоваться вероятностью данного её значения. Верная постановка вопроса заключается в том, чтобы узнать вероятность того, что данная величина лежит в интервале от, скажем x до x+dx. Эта вероятность математически равна:

$dW=w(x)dx$

Здесь w(x) – некоторая функция, называемая плотностью вероятности. Её размерность обратна размерности случайной величины x.

И, наконец, ещё необходимо сказать довольно очевидную вещь, что вероятность достоверного события, или сумма всех вероятностей полной группы несовместимых событий равна единице.
В принципе этих определений нам достаточно, чтобы показать вывод распределения Максвелла, а далее распределения Больцмана.

Итак, рассмотрим идеальный газ (это может быть и электронный газ, настолько разрежённый, что взаимодействием электронов можно пренебречь). Каждая частица этого газа обладает скоростью v или импульсом $p=m_0v$ и все эти скорости и импульсы могут быть какими угодно. Значит эти параметры являются случайными величинами и нас будет интересовать плотность вероятности $w_p$ .

Далее удобно ввести представление о пространстве импульсов. Отложим по осям системы координат компоненты импульса частицы (см. рис. 3)

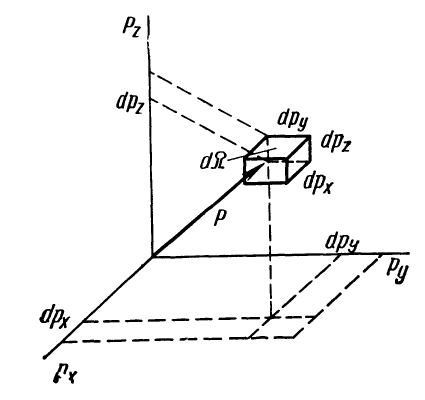
Рис. 3

Нам необходимо выяснить, чему равна вероятность того, что каждая компонента импульса лежит в диапазонах:

$p_x div (p_x + dp_x); p_y div (p_y + dp_y); p_z div (p_z + dp_z)$

Т.е., что тоже самое, конец вектора p находится в прямоугольном объёме dΩ:

$dOmega=dp_xdp_ydp_z$

Максвелл положил два постулата, опираясь на которые вывел распределение по импульсам. Он предположил:

А) Все направления в пространстве равноправны и это свойство называется изотропностью, в частности изотропностью плотности вероятности $w_p$ .

Б) Движение частиц по трём взаимно перпендикулярным осям независимы, т.е. значение импульса $p_x$ , не зависит от того, каково значение его остальных компонент $p_y$ и $p_z$ .

Частицы двигаются в различных направлениях, как в положительную сторону, так и в отрицательную. Т.е., например, по оси x значение импульса может принимать значение как $p_x$ , так и $-p_x$ . Но плотность вероятности чётная функция (т.е. при отрицательных значениях аргумента, функция положительная), поэтому она зависит от квадрата $p_x$ :

$w_{px}=phi(p_x^2)$

Из свойств изотропности (см. выше) следует, что плотности вероятности двух остальных компонент выражаются аналогично:

$w_{py}=phi(p_y^2); w_{pz}=phi(p_z^2)$

По определению вероятность того, что импульс p попадёт в объём dΩ равна:

$dW=w_pdOmega$

Вспомним, что мы выше выяснили, что для независимых событий эта вероятность может быть выражена через произведение вероятностей событий каждой компоненты:

$w_pdOmega=w_{px}dp_xw_{py}dp_yw_{pz}dp_z=phi(p_x^2)phi(p_y^2)phi(p_z^2)dp_xdp_ydp_z$

Следовательно:

$w_p=psi(p^2)=phi(p_x^2)phi(p_y^2)phi(p_z^2)$

Прологарифмируем это выражение и получим:

$ln psi=ln phi(p_x^2) + ln phi(p_y^2) + ln phi(p_z^2)$

Затем продифференцируем это тождество по $p_x$ :

$frac{psi^{'}}{psi}2p_x=frac{phi^{'}}{phi}2p_x$

, где штрихом обозначена производная соответствующей функции по её сложному аргументу.

После сокращения в этом выражении на $2p_x$ получаем:

$frac{psi^{'}(p^2)}{psi(p^2)}=frac{phi^{'}(p_x^2)}{phi(p_x^2)}$

Тоже самое относится и к другим компонентам импульсов, соответственно получаем:

$frac{psi^{'}(p^2)}{psi(p^2)}=frac{phi^{'}(p_y^2)}{phi(p_y^2)}; frac{psi^{'}(p^2)}{psi(p^2)}=frac{phi^{'}(p_z^2)}{phi(p_z^2)}$

Отсюда следуют важные соотношения:

$frac{phi^{'}(p_x^2)}{phi(p_x^2)}=frac{phi^{'}(p_y^2)}{phi(p_y^2)}=frac{phi^{'}(p_z^2)}{phi(p_z^2)}$

Из этих выражений видно, что отношения производной функции по самой функции от той или иной компоненты импульса является постоянной величиной, соответственно мы можем написать следующим образом (обозначим постоянную как $- beta$ ):

$frac{phi^{'}(p_x^2)}{phi(p_x^2)}=-beta$

Решая это дифференциальное уравнение, получим (как решаются такие уравнения можно найти в любом учебнике по обыкновенным дифференциальным уравнениям):

$phi(p_x^2)=Ce^{-beta p_x^2}$

Где C и β – константы, которые нам предстоит ещё вывести (в следующей статье). Таким образом, из условия изотропности и независимости движения по осям координат следует, что вероятность $dW_{px}$ того, что компонента импульса $p_x$ окажется в интервале $dp_x$ определяется соотношением:

$dW_{px}=Ce^{-beta p_x^2} dp_x$

, а вероятность dW того, что импульс окажется в объёме dΩ, равна (вспомните произведение вероятностей независимых событий):

$dW=C^3e^{-beta p^2} dOmega$

В следующей статье мы завершим вывод распределения Максвелла, выясним физический смысл этого распределения и подойдём непосредственно к выводу распределения Больцмана.

Автор: rezerford

Источник