Разбираемся в физике частиц: 8) как частицы взаимодействуют с полями

1. Шар на пружине, ньютоновская версия
2. Квантовый шар на пружине
3. Волны, классический вид
4. Волны, классическое уравнение движения
5. Квантовые волны
6. Поля
7. Частицы – это кванты

В предыдущей статье серии я объяснил, что частицы природы – это кванты релятивистских полей, удовлетворяющие уравнениям движения класса 0 и класса 1. Но чего я пока не сказал, так что это утверждение, к счастью, верно лишь отчасти. Реальные уравнения всегда чуть более сложные, таким образом, что взаимосвязь частиц и полей остаётся, но при этом становятся возможными гораздо более разнообразные явления и процессы, включая появление частиц после столкновения других частиц, распад частиц на другие частицы, и рассеяние частиц друг с друга, а также формирование таких интересных объектов, как протоны и нейтроны, атомные ядра и атомы. Я не смогу объяснить всё это подробно, но в этой статье дам вам вводную того, как всё это работает.

Ключевое различие между уравнениями, которые я называл «классом 0» и «классом 1», и уравнениями, значимыми для реальной физики, в том, что в реальных уравнениях есть дополнительные члены, зависящие от двух или большего количество полей, а не только от одного. То есть, допустим, вместо уравнения класса 0 для релятивистского поля Z(x,t), выглядящего, как

для реальных полей уравнения выглядят больше похожими на это:

Где y и y' – числа (обычно меньше 1), Z – краткая запись Z(x,t), а A(x,t) и B(x,t) – пара других полей. В таких уравнениях можно ожидать появления таких членов, как A(x,t)Z(x,t), или A(x,t)² Z(x,t), или Z(x,t) ², или даже A(x,t)d²Z/dt², и т.д. Какие члены могут, а какие не могут появляться, зависит от подробностей участвующих в процессе полей. Правила строгие, но довольно запутанные, так что не будем пока в них углубляться. В целом из экспериментов мы установили (и поняли с теоретической точки зрения), что в природе:

• Любой допустимый в принципе член (сохранение электрического заряда или соответствие относительности Эйнштейна) появляется в уравнениях,
• но члены со многими полями обычно очень малы и незначительны по сравнению с членами с одним, двумя, и иногда тремя полями (члены с производными времени или пространства тоже обычно малы).

Следовательно, в большинстве интересных физических процессов можно сфокусироваться на всех допустимых членах с одним, двумя или тремя полями.

Немного терминологии. Члены в уравнениях с полями в первой степени называются линейными. Все члены в наших уравнениях класса 0 или 1 были линейными. Члены с двумя или тремя полями называются квадратичными или кубическими; в общем, они называются нелинейными. Все интересные явления нашего мира появляются из-за нелинейных членов в уравнениях движения – а именно, взаимодействия полей друг с другом и с самими собой. Давайте изучим одно из них.

Появление новой волны из резонанса двух других

Чтобы получить представление о том, насколько интересным всё может стать, возьмём три поля, A(x,t), B(x,t), C(x,t), и упрощённую ситуацию. Допустим, поля A и B примерно удовлетворяют уравнениям класса 0 (и содержат безмассовые кванты), а поле C удовлетворяет уравнениям класса 1 (содержит волны с минимальной частотой ν_min, и соответственно, кванты массой m = h ν_min / c ², где h – постоянная Планка). А ещё мы добавим в их уравнения нелинейные члены. Конкретно вот так (для краткости будем писать «A» вместо «A(x, t)», и так далее, c – скорость света, y – число, обычно меньшее 1):

Мелкий шрифт: я добавил нелинейные члены во все три уравнения потому, что наличие таких членов в одном из уравнений и отсутствие их в других приведёт к противоречиям; к примеру, энергия не будет сохраняться. Для описываемого мною процесса нам нужно будет рассмотреть только нелинейные члены в уравнениях движения поля С.

Посмотрим, что произойдёт с таким набором уравнений, если волна поля А встретится с волной поля В. В принципе мы можем догадаться об этом, применив метод пристального разглядывания. Если в поле А есть волна, тогда A(x,t) ненулевое вблизи её. Когда волны полей А и В перекрывают друг друга, то результат умножения A(x,t) и В(x,t) становится ненулевым. Теперь обратимся к уравнению для С: изменения поля С во времени и в пространстве (два члена в левой части) связаны с произведением А и В (один из членов в правой части).

Так что даже если поле С нулевое, когда A(x,t)B(x,t) становится ненулевым, то и C(x,t) вскоре станет ненулевым на том же участке. Короче, в результате встречи волн А и В произойдёт некое малое возмущение поля С.

Мелкий шрифт: вас может заинтересовать – после того, как С станет ненулевым, станет ли член A(x,t) C(x,t) в уравнении движения для поля В причиной дополнительного возмущения поля В. Ответ – да, но этот эффект будет ещё меньшим. Пока мы его проигнорируем, а позже узнаем, почему так стоило поступить.

На рис. 1 показана волна с частотой ν в поле А (зелёная), встречающаяся с волной частоты ν поля В (синяя). Я уравнял частоты для простоты и симметрии. Позже мы увидим, почему другие случаи сводятся к этому. Скорость ν можно оценить, наблюдая за зелёной волной и за вертикальной чертой, находящейся в одной точке пространства и колеблющейся вместе с волной.

Ниже оранжевым показано произведение A(x,t)B(x,t); видно, что оно становится ненулевым при наложении двух волн. Также видно, что оно колеблется во времени. Можно увидеть (сравнивая её с колеблющейся вертикальной чертой), что A(x,t)B(x,t) колеблется в два раза быстрее. Запомните этот важный факт. В общем случае, если волна частоты ν₁ встречается с волной частоты ν₂, то их произведение будет колебаться с частотой ν₁ + ν₂. И ещё одно: можно заметить, что колебания АВ не двигаются вправо или влево, они остаются на месте. Позже мы увидим, почему это важно.

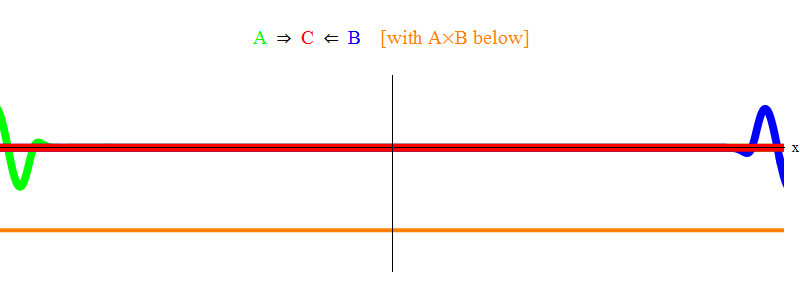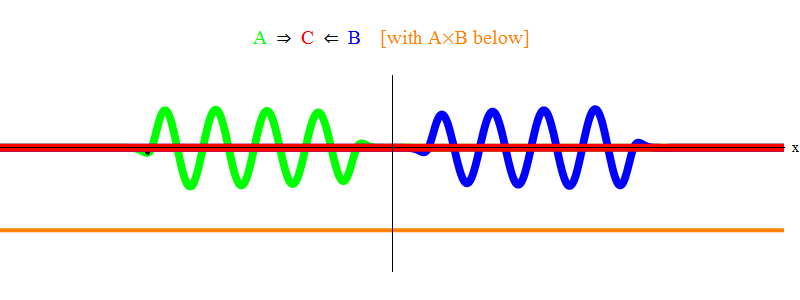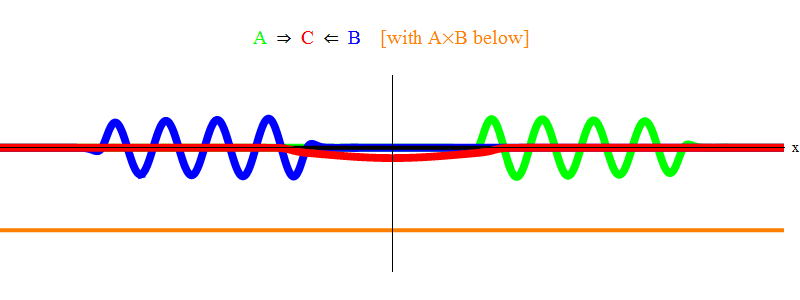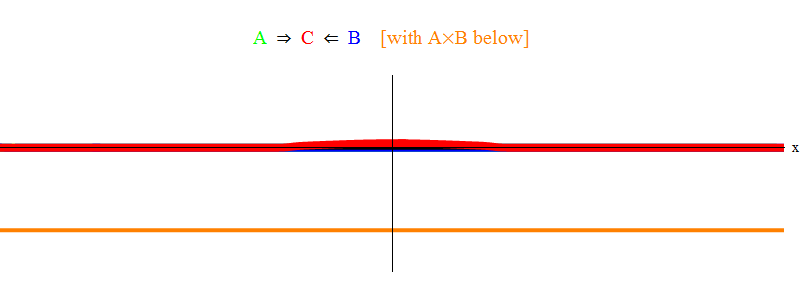
Рис. 1

Как же ненулевое значение АВ влияет на С? Ответ сильно зависит от частоты ν. Сначала я дам вам готовый ответ, а потом примерное объяснение причины. Это, по сути, резонанс. Резонанс – неотъемлемое явление всех колебаний (вибраций), включая волны. Я уже описывал, как шар на пружине колеблется с естественной частотой, и как колебательная сила, толкающая шар, может привести к резонансу, если частота колебаний силы совпадёт с естественной частотой шара на пружине.

Поняв резонанс, вы увидите, что поле С, колеблясь с минимальной частотой и нулевой горизонтальной скоростью, ведёт себя, как шар на пружине, а АВ ведёт себя как колебательная сила, пытающаяся заставить мяч колебаться. Поэтому, явление резонанса возникает, если частота колебаний АВ — 2ν – оказывается минимальной частотой поля С – ν_min. Конкретнее:

• Если 2 ν не равно ν_min — если силы не в резонансе – тогда на участке, где АВ не равно нулю, С начнёт колебаться нерегулярно, с небольшой амплитудой.
• Если 2 ν = ν_min — если сила в резонансе – тогда С будет колебаться плавно, с большой амплитудой, на участке, где АВ не равно нулю, и продолжит колебаться даже тогда, когда АВ снова станет равным нулю.

Рис. 1 показывает только резонансную ситуацию 2 ν = ν_min. Видно, что когда волна А проходит волну В, они оставляют после себя стационарную волну С, колеблющуюся с частотой ν_min. Мелкий шрифт: на рис. показан набросок, не точное решение уравнений. У точного решения будет множество мелких сложных особенностей, которые затмят основной физический смысл, так что я удалил их для ясности. Позже мы рассмотрим ситуацию без резонанса, которая гораздо сложнее, но и важнее для физики.

Появление новой частицы из аннигиляции двух других

Я только что продемонстрировал вам, что нелинейные члены АВ в уравнении С могут привести к тому, что наложение волн А и В породит колебания поля С, если сумма частот полей А и В равна минимальной частоте поля С. Но что, если у этих волн была очень маленькая амплитуда? Что может случиться, если один квант поля А встретится с одним квантом поля В?

• Если частоты АВ входят в резонанс с полем С, тогда может возникнуть квант поля С, то есть реальная частица С, а кванты А и В исчезнут – «аннигилируют».
• Также кванты А и В могут просто пройти друг мимо друга, без создания частицы С.
• Законы квантовой механики предполагают, что вероятность создания частицы С пропорциональна квадрату числа y, которое перемножается с АВ в уравнении движения С.
• Если частоты в резонанс не входят, реальная частица С не появится. Однако в поле С может возникнуть временное возмущение, пример того, что часто называют «виртуальной частицей» С, и в этом случае кванты А и В могут исчезнуть. Что получается в результате такого возмущения? Я частично описал этот процесс в конце статьи, в разделе «хвосты».

Таково общее положение вещей. Давайте углубимся в детали.

Что для частиц, то есть квантов полей А, В и С означает быть в резонансе или не в резонансе? Стоит помнить, что энергия кванта связана с его частотой благодаря уравнению E = h ν. Так что переведём наше обсуждение волн в обсуждение частиц.

Допустим, что наши волны на полях А и В состоят каждая из одного кванта. Эти кванты безмассовые, поскольку А и В удовлетворяют уравнениям класса 0. Точнее, линейные члены в их уравнениях движения такие же, как у уравнений класса 0. Поскольку у квантов А и В одна частота, они обладают одинаковой энергией, E = h ν. Поскольку импульс безмассового кванта равен p = E/c, у квантов А и В будут импульсы, равные по величине h ν/c, но противоположные по направлению, поскольку один из них движется, влево, а другой – вправо. Следовательно:

• Общая энергия двух квантов вместе составит 2hν.
• Общий импульс двух квантов вместе будет нулевым.

Поскольку энергия и импульс сохраняются, общая энергия после столкновения двух квантов останется равной 2hν, а общий момент останется нулевым.

В случае с волнами мы видели, что поскольку уравнение для С содержит член вида АВ, существует резонанс, когда частота АВ (работающая, как колебательная сила), совпадает с минимальной частотой С (работающим, как шар на пружине). Переведём это утверждение в кванты.

Частота АВ будет 2 ν, поэтому энергия произведения А и В, когда волны А и В состоят из одного кванта, равна сумме энергий А и В.

Минимальная частота С равна ν_min, что значит, что у стационарного кванта поля С импульс равен 0, а энергия

Где m – масса кванта С.

Для резонанса требуется 2 ν = ν_min, то есть:

Короче говоря, резонанс происходит, когда суммы равных энергий частиц А и В (у которых в нашем случае одинаковые по величине и противоположные по направлению импульсы) как раз хватает для создания стационарной частицы С! В процессе происходит аннигиляция частиц А и В – их энергия полностью уходит в создание частицы С. Это показано (схематично) на рис. 2, который вам нужно сравнить с рис. 1.

Рис. 2

Рассуждения

Я только что показал вам процесс A + B → C. В моём объяснении я использовал три разных типа частиц, чтобы избежать путаницы. Но та же идея позволяет проходить процессам вида A + A → C (к примеру, глюон + глюон → частица Хиггса, а в основном именно так частицу Хиггса получают в Большом адронном коллайдере) и процессам вида A + A* → C, где A* — античастица для А (к примеру, кварк + антикварк → Z-частица, и именно так обычно получают Z-частицы на БАК). Нужно лишь поменять незначительные детали, а суть остаётся такой же.

Ещё один процесс, представляющей собой ту же идею, только обращённую во времени – распад частиц. Распад частицы Хиггса на два фотона или Z-частицы на кварк и антикварк по сути происходит так, как анимация на рис. 2, идущая в обратном направлении.

Хвосты

1. Если член АВ возмущает поле С без резонанса – если 2 ν ≠ ν_min — что произойдёт? Вы можете вспомнить, что если вы толкаете качели с ребёнком не с той частотой, или прикладываете к шару на пружине силу, колеблющуюся с частотой, не совпадающей с собственной частотой колебаний, вы получите неровное колебание с малой амплитудой. В текущем контексте то же самое происходит с полем С. Поле С как-то поведёт себя, но это не приведёт к появлению хорошо ведущего себя кванта С. Оно просто немного поволнуется. Это плохое возмущение – один из примеров т.н. «виртуальных частиц С» – но это не частица (квант волны поля С), несмотря на её название. Её масса отличается от массы частицы С; она может быть крупнее или мельче. В отличие от частицы С она не существует сама по себе какое-то продолжительное время. И она не удовлетворяет условиям по амплитуде, которым должны удовлетворять настоящие кванты. Вместо этого, в отличие от существующей какое-то время частицы С с рис. 2, нерезонансное возмущение существует только тогда, когда А пересекается с В.

Но это не означает, что она ни на что не влияет. К примеру, она может заставить частицы А и В отскочить друг от друга.

Вообще, в трёхмерном пространстве отскок, или рассеяние, может привести к тому, что А движется в любом направлении, а В – в противоположном. Примеры таких процессов включают рассеяние электрона и позитрона благодаря виртуальному фотону, или рассеяние кварка и антикварка благодаря виртуальному глюону.

В присутствии других полей, D и Е, взаимодействующих с С и участвующих в уравнении движения С

Могут происходить гораздо более интересные процессы:

A + B → C_{возмущение} → D + E

Именно так: частицы А и В могут аннигилировать благодаря виртуальной частице С, и привести к появлению новых частиц D и Е. Это второй способ создания новых частиц! К примеру, электрон может столкнуться с позитроном, аннигилировать через виртуальный фотон (помним, что это означает «через возмущение фотонного поля на частоте, не совпадающей с резонансной»), и превратиться в мюон и антимюон, или кварк и антикварк. Нижний кварк и верхний антикварк могут столкнуться, аннигилировать через виртуальную W-частицу, и превратиться в электрон и антинейтрино. Или два глюона могут столкнуться, аннигилировать через виртуальный глюон, и превратиться в верхний кварк и верхний антикварк (это самый распространённый способ получения верхних кварков на БАК).

2. Что, если две волны в полях А и В обладают разными частотами, ν_A и ν_B? При подходящих частотах частицы С всё ещё могут появиться, но условия резонанса будут другими, и созданная частица С не будет стационарной. Давайте разберёмся.

Если у них разные частоты, у двух сталкивающихся безмассовых квантов будут

• Различные энергии и
• Различные импульсы и (тут плюс означсет вправо, минус – влево).

Общий импульс p_A + p_B теперь ненулевой. Но импульс сохраняется. Поэтому, если частица С может возникнуть в результате аннигиляции частиц А и В, у неё будет импульс p_С = p_A + p_B, поэтому она будет двигаться влево или вправо, а не стоять на месте. Если ν_А > ν_B, тогда она будет двигаться вправо, иначе – влево.

Сколько энергии требуется для создания движущейся частицы С? Для этого нужно больше энергии, чем для покоящейся – как у любой массивной частицы, её энергия и импульс должны удовлетворять

Что означает, что E_С = mc², если p_С = 0, или больше, если импульс ненулевой. Закон сохранения энергии и импульса говорит нам, что:

Откуда я взял последнее уравнение? Для безмассовой частицы p = E/c, а для наших сталкивающихся частиц А и В их импульсы направлены противоположно, поэтому они отличаются по знаку. Подставим это в предыдущее уравнение и получим:

Члены E_A² и E_B² взаимно уничтожаются, и переведя члены E_A E_В в левую часть, получим:

Поделив на h² и используя соотношение m = hν_min / c², получим условие резонанса:

Что корректно сводится, когда ν_A = ν_В, до уравнения для неподвижной частицы С, 2 ν= ν_min. Если это условие не удовлетворяется, то частицу С создать нельзя. Если удовлетворяется, то можно.

3. Я отметил, что точно так же, как уравнение движения для поля С содержит член АВ, так и уравнение для В содержит член АС. Вспомним эти уравнения:

Так что, если наложение волн А и В приводит к появлению волны в поле С, делая его ненулевым, как на рис. 1, не надо ли нам волноваться по поводу того, что эта новая волна С наложится на существующую волну А и приведёт к изменению в поле В? Я отвечал, что «да, но мы можем этим пренебречь». Пренебрегать мы можем из-за комбинации двух причин.

Во-первых, из-за числа «y», появляющегося перед перемножениями АВ и ВС. Воздействие на поле С члена АВ пропорционально y, умноженному на А, умноженному на В. Воздействие на поле В члена АС также пропорционально y, умноженному на А, умноженному на С, но это в свою очередь будет равно y², умноженному на А, умноженному на А, умноженному на В. Так что пока y меньше 1, y² будет меньше у, поэтому воздействие на В члена АС мало по сравнению с воздействием на С члена АВ – по крайней мере, для небольших волн А и В. На практике эти волны обычно небольшие: частица А – один квант волны в поле А, поэтому волна у А обладает малой амплитудой.

Из чего вытекает вторая, более странная, но более убедительная причина: мы видели, что если один квант А встречается с одним квантом В и превращается в один квант С, то волны А и В исчезают (аннигилируют). После создания С уже нет никакой волны А, поэтому АС равно нулю, то есть на поле В воздействия не происходит.

И последний подвох: хотя я не могу доказать это без дополнительных выкладок, даже если у А и В волны состоят из одного кванта, как на рис. 2, то процесс на рис. 2 был бы гораздо более сложным, если бы y было гораздо больше 1. Так что простота рассказанной мною истории требует небольших значений у. В природе у большинства нелинейных членов в физике частиц у обычно маленькие, поэтому то, что я рассказал, относится к большинству практически применимых ситуаций. Исключения очень интересные – они приводят к созданию таких сложных объектов, как протоны и другие адроны.

Автор: Вячеслав Голованов

Источник