1) шар на пружине, ньютоновская версия
2) квантовый шар на пружине
3) волны, классический вид
4) волны, классическое уравнение движения
5) квантовые волны
6) поля
Вот мы, наконец, и добрались до нашей цели: понять, что на самом деле представляют собой те штуки, что мы зовём «частицами», а именно – электроны, фотоны, кварки, глюоны и нейтрино. Всё, это, конечно же относится к современной науке. Стоит помнить, что в науке нет никаких гарантий того, что текущее понимание не будет в дальнейшем углублено.
Предыдущая статья описывала, что такое поля – объекты, обладающие значением в любой точке пространства и в любой момент времени (функции от пространства и времени), удовлетворяющие уравнению движения, и физически осмысленные в плане того, что они способны переносить энергию из одного места в другое и влиять на физические процессы Вселенной.
Мы узнали, что большинство знакомых нам полей описывают свойство среды, такой, как высота верёвки или давление в газе. Но также мы узнали, что в эйнштейновской теории относительности существует особый класс полей, релятивистские поля, не требующие среды. Или, по крайней мере, если у них и есть среда, она весьма необычная. Ничто в уравнениях поля не требует наличия какой-то среды и не говорит о том, какое свойство этой среды описывают релятивистские поля.
Так что пока мы будем рассматривать релятивистские поля как элементарные физические объекты вселенной, а не как определённые свойства неизвестной среды. Будет ли среди физиков поддерживаться такая точка зрения и дальше – покажет время.
Мы рассматривали два класса релятивистских полей, и теперь мы изучим их чуть подробнее. Они удовлетворяют либо уравнению движения Класса 0, где cw = c (где c – универсальный предел скорости, часто называемый «скоростью света»).
Или уравнениям движения Класса 1, где cw=c
В предыдущей статье показано, что μ – минимальная частота волны в таких полях. В этой статье мы будем обозначать её νmin.
Почему универсальный предел скорости часто называют скоростью света? Волны с уравнением класса 0 перемещаются со скоростью cw. Свет (общий термин, обозначающий электромагнитные волны любой частоты), перемещаясь через пустое пространство, удовлетворяет релятивистскому уравнению класса 0, поэтому волны света (и волны любых релятивистских полей, удовлетворяющих релятивистскому уравнению класса 0) перемещаются со скоростью c.
Более того, в той же статье мы видели, что если у поля класса 1 есть волна с амплитудой А, частотой ν, длиной волны λ и равновесным состоянием Z0, то уравнение движения требует, чтобы частота и длина волны были связаны с величиной μ = νmin, появляющейся в уравнениях, формулой
Это пифагорова формула – её можно при желании представить в виде треугольника, как на рис. 1. Минимальная частота любой волны равна νmin, а присвоение ν = νmin (и, следовательно, при λ → ∞), соответствует сжатию треугольника до вертикальной линии (рис. 1, внизу). Также можно получить схожее соотношение класса 0, сделав μ = νmin нулевым. Потом можно извлечь квадратный корень, и получить
Это уже треугольник, сжатый до горизонтальной линии (рис. 1, справа). В этом случае минимальная частота равна нулю. Поле может колебаться как угодно медленно.
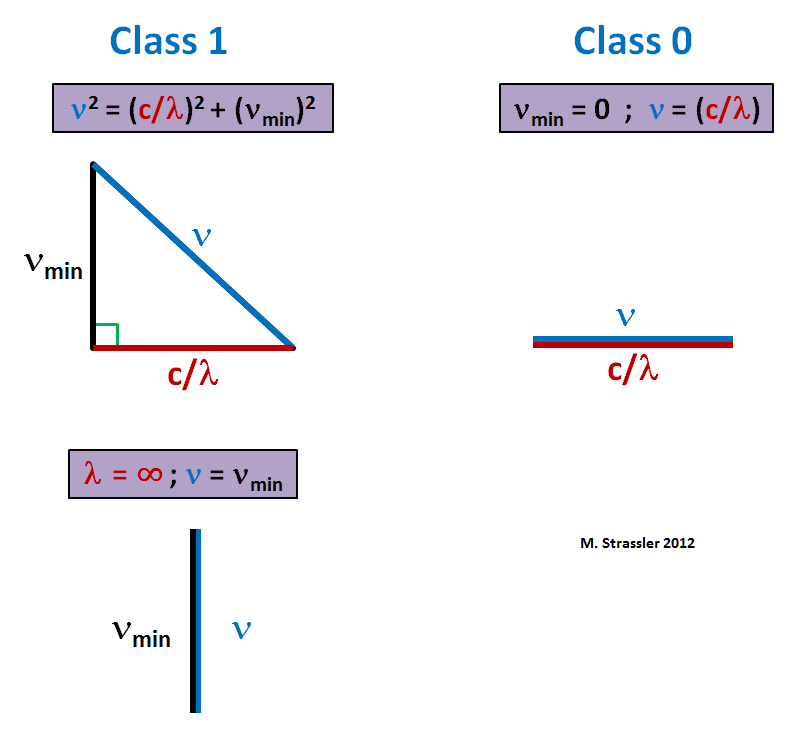
Рис. 1
На А никаких ограничений нет. Но это оттого, что мы игнорируем квантовую механику. Пришло время изучить релятивистские квантовые поля.
Релятивистские квантовые поля
Реальный мир – квантово-механический, поэтому амплитуда А не может быть любой. Она принимает дискретные значения, пропорциональные квадратному корню из n, неотрицательного целого числа, обозначающего количество квантов колебаний в волне. Хранящаяся в волне энергия равна
Где h – постоянная Планка, обязательно появляющаяся там, где квантовая механика имеет значение. Иначе говоря, энергия, связанная с каждым квантом колебаний, зависит только от частоты колебаний волны, и равна
Это соотношение впервые было предложено, конкретно для волн света, Эйнштейном в 1905 году, в его объяснении фотоэлектрического эффекта.
Но вспомним наше пифагорово соотношение частоты и длины волны. Если мы умножим его на h2, мы получим, что для кванта поля класса 1
Выглядит знакомо. Мы уже знаем, что любой объект в эйнштейновской теории относительности должен удовлетворять уравнению, описывающему его энергию, импульс и массу:
Ещё одно пифагорово соотношение. Минимальная энергия объекта равна mc2, что напоминает утверждение о минимальной частоте, которой может обладать волна класса 1, νmin. У нас может возникнуть искушение предположить, что, вероятно, для кванта релятивистского поля
Первое уравнение впервые появилось в работе Луи Де Бройля в 1924 году – почти через 20 лет после Эйнштейна. Почему это заняло так много времени? Я не знаю.
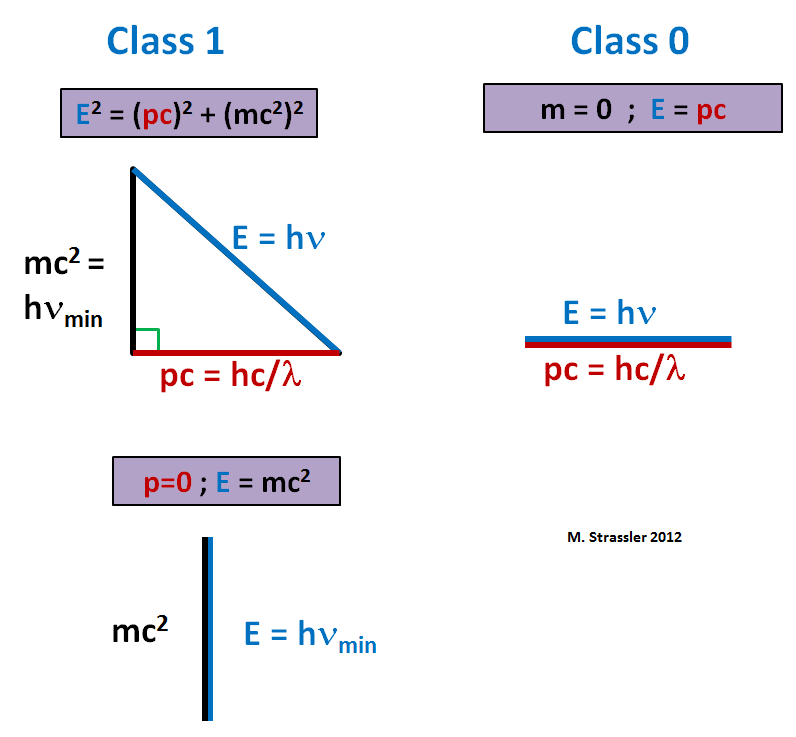
Рис. 2
Имеет ли это смысл? Как мы отмечали, в релятивистские поля класса 0 входят и электрические поля, а их волны – это электромагнитные волны, то есть, свет. Версия формулы (*), которую мы получаем для квантов класса 0, такая же, как для полей класса 1, у которых μ = νmin приравнивается к нулю – то есть, m = 0. Извлечём квадратный корень, и получим
Или Эйнштейновское уравнение для безмассовых частиц. А кванты электромагнитных волн (включая все виды света: видимый, ультрафиолет, инфракрасный, радиоволны, гамма-излучение, и т.п., отличающиеся только частотой, и, следовательно, энергией квантов) и правда будут безмассовыми частицами – как только мы применим указанную выше пару уравнений (**) и (***). Это фотоны.
Из уравнения (***) мы, наконец, можем подсчитать массу частицы. Каждая обладающая массой частица – это квант поля класса 1. Минимальная частота таких волн равна νmin. Минимальная энергия одного кванта такой волны равна h, помноженной на частоту. А масса частицы – просто минимальная энергия, делённая на c2.
Если мы хотим понять, откуда берётся масса частицы, нам нужно понять, что определяет νmin, и почему вообще существует минимальная частота. Для таких частиц, как электроны и кварки, это полностью неясно, но известно, что в этом важную роль играет поле Хиггса.
Заключим: частицы природы – это кванты релятивистских квантовых полей. Безмассовые частицы – это кванты волн полей, удовлетворяющих уравнению класса 0. Обладающие массой соответствуют полям уравнения класса 1. Всяких деталей существует множество, но этот факт – одно из основных фундаментальных свойств нашего мира.
Действительно ли эти кванты ведут себя как частицы?
Мы представляем себе частицы, как частички пыли или песчинки. Кванты в этом смысле частицами не являются – это волны, у которых для определённой частоты есть минимальные энергия и амплитуда. Но они ведут себя так похоже на частицы, что нас можно простить за использование слова «частица» в их описании. Посмотрим, почему так.
Если поднять волну в воде, и позволить ей пройти через камни, лежащие неглубоко под поверхностью, часть волны перейдёт линию камней, а часть отразится, как показано на рис. 3. То, какая именно часть волны перейдёт линию, зависит от формы камней, их близости к поверхности, и т.п. Но суть в том, что часть волны передаётся через камни, а часть отразится. Часть энергии волны пойдёт в том же направлении, часть пойдёт в обратном.
Рис. 3
Но если вы отправите один фотон в сторону отражающего стекла, этот фотон либо пройдёт сквозь него, либо отразится (рис. 4). Точнее сказать, если вы измерите поведение фотона, то узнаете, отразился он или передался. Если не измерите – невозможно будет сказать, что произошло. Добро пожаловать в болото квантовой механики. Фотон – это квант. Его энергию нельзя поделить на часть, которая прошла через стекло, и часть, которая отразилась – потому что тогда с каждой стороны будет меньше одного кванта, что запрещено. (Мелкий шрифт: стекло не меняет частоту фотона, поэтому энергию нельзя разделить между двумя или более квантами меньших частот). Так что фотон, хотя это и волна, ведёт себя как частица в этом случае. Он либо отражается от стекла, либо нет. Отражается он, или нет – этого квантовая механика не предсказывает. Она даёт только вероятность отражения. Но она предсказывает, что, что бы там ни произошло, фотон будет путешествовать как единое целое и сохранять свою идентичность.
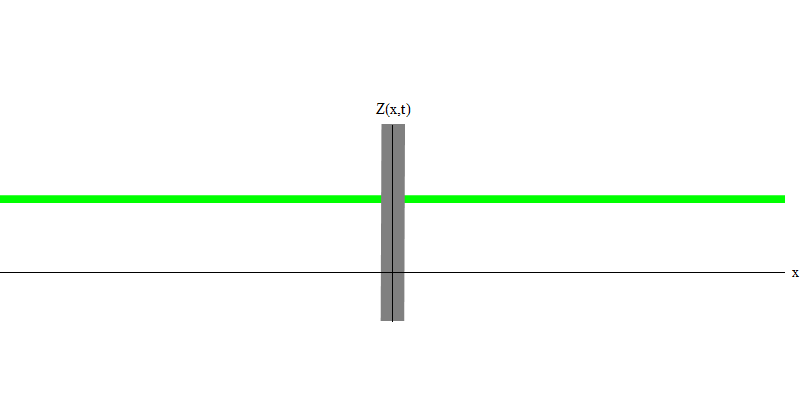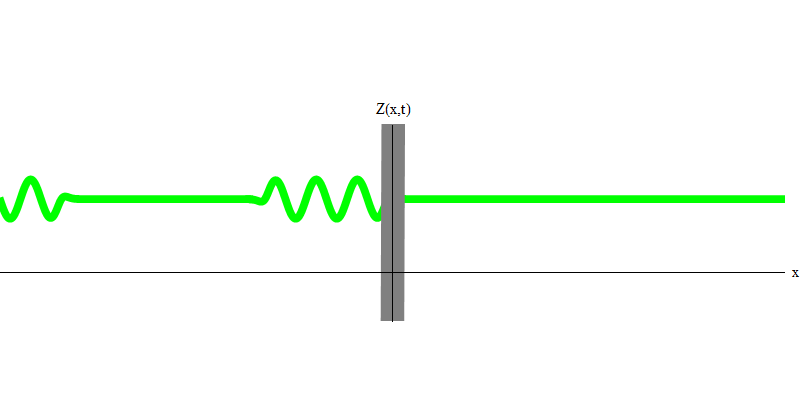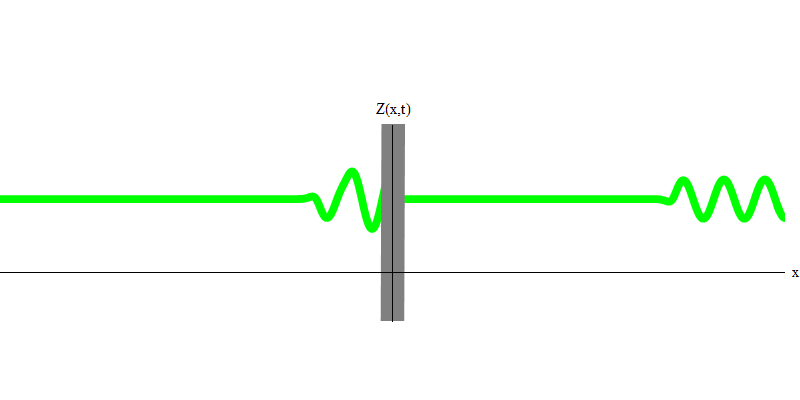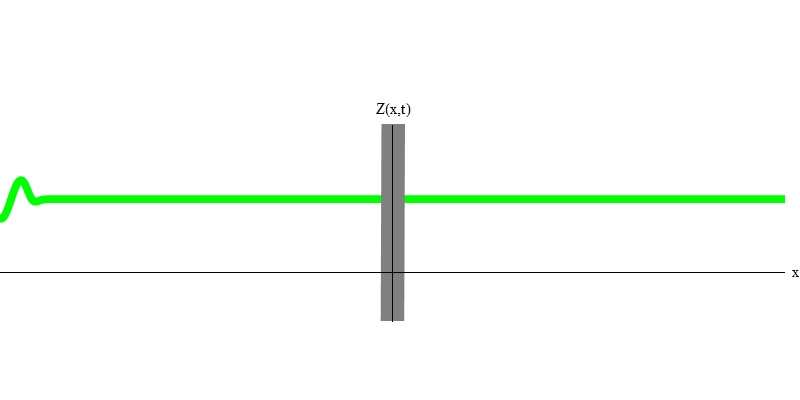
Рис. 4
А что будет с двумя фотонами? Это зависит. К примеру, если фотоны испущены в разное время из разных мест, то наблюдатель увидит два кванта, разделённых в пространстве, и, вероятно, двигающихся в разных направлениях (рис. 5). У них могут быть и разные частоты.
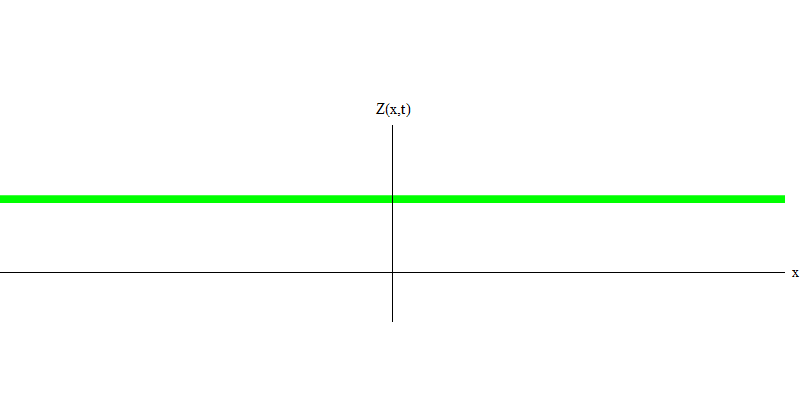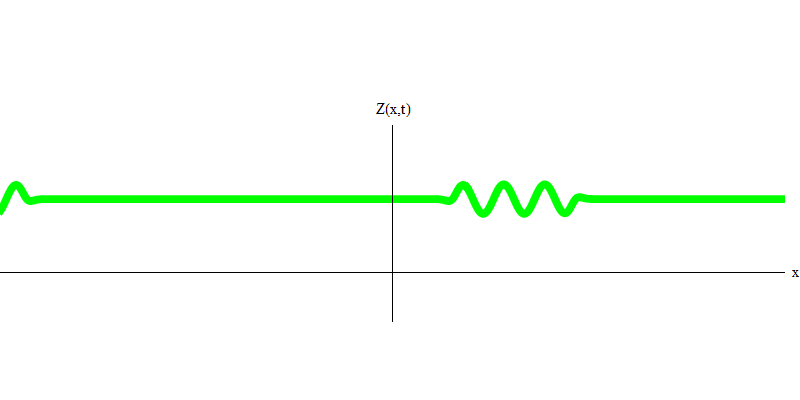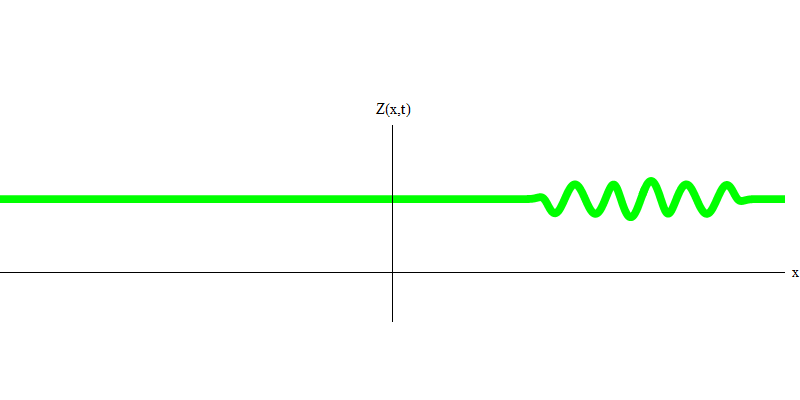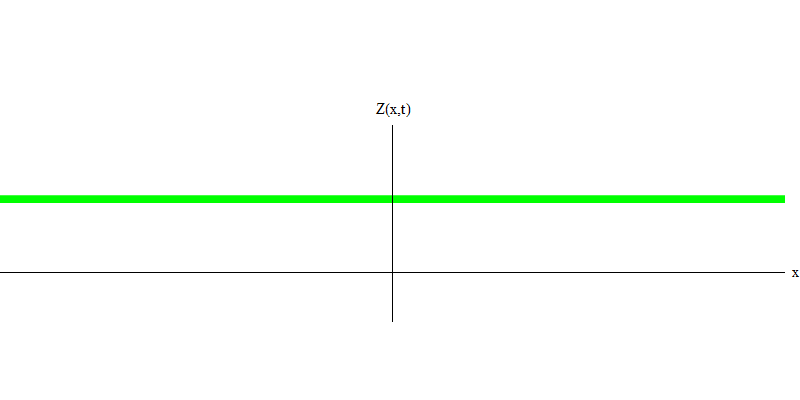
Рис. 5: независимые кванты
В особом случае, когда два фотона испускаются совместно и идеально синхронно (как в лазерах), они ведут себя, как показано на рис. 6. Если мы отправим комбинацию из двух фотонов на стекло, то сможет случиться не две, а три вещи. Либо оба фотона пройдут через стекло, либо оба отразятся, либо один пройдёт, а другой отразится. От стекла отразятся 0, 1 или 2 фотона – других вариантов нет. В этом смысле кванты света опять ведут себя, как частицы, как маленькие мячики – если бросить два мяча в решётку, в которой есть отверстия, то от решётки смогут отразиться 0, 1 или 2 мяча, и через отверстия пройдут 0, 1 или 2 мяча. Не существует возможности, в которой от решётки отразится 1,538 мяча.
Рис. 6
Но это фотоны, которые, не имея массы, обязаны двигаться со скоростью света и E = p c. Что насчёт частиц с массой, вроде электронов? Электроны – это кванты электрического поля, и, как и фотоны, их можно испускать, поглощать, отражать или передавать как единое целое. У них есть определённые энергия и импульс, 
, где me — это масса электрона. Отличие электронов от фотонов в том, что они движутся медленнее света, поэтому могут и покоиться. Зарисовка такого события (в квантовой механике из-за принципа неопределённости ничто не может быть по-настоящему статичным) стационарного электрона дана на рис. 7. Это волна минимальной частоты, полученной присвоением длине волны очень большого, практически бесконечного, значения. Поэтому пространственная форма волны на рис. не демонстрирует никаких извилин – она просто колеблется во времени.
Рис. 7
Так что, да, на самом деле кванты ведут себя очень похоже на частицы, и потому называть электроны, кварки, нейтрино, фотоны, глюоны, W-частицы и частицы Хиггса «частицами» не будет катастрофическим обманом. Но слово «квант» подходит для этого лучше – потому что это именно кванты.
Чем фермионы и бозоны отличаются друг от друга
• Все элементарные частицы делятся на фермионы и бозоны.
• Фермионы (включая электроны, кварты и нейтрино) удовлетворяют принципу запрета Паули – два фермиона одного типа не могут делать одно и то же.
• Бозоны (включая фотоны, W и Z частицы, глюоны, гравитоны и частицы Хиггса) другие: два или более бозонов одного типа могут делать одно и то же.
Именно поэтому из фотонов можно делать лазеры – поскольку они бозоны, они могут находиться в одинаковом состоянии и порождать мощный луч одного света. Но лазер нельзя сделать из электронов, являющихся фермионами.
Как проявляет себя это различие на языке математики? Оказывается, что приводимые мною формулы подходят для бозонов, а для фермионов их нужно изменить – слегка, но с большими последствиями. Для бозонов у нас будет:
Что означает, что энергия каждого кванта равна h ν. Это подразумевает, что кванты-бозоны могут делать одно и то же; когда n больше 1, у бозонного поля волна будет состоять из нескольких квантов, колеблющихся и движущихся совместно. Но для фермионов:
which means each quantum has energy h ν. That implies that boson quanta can be made to do exactly the same thing; when n is greater than 1, the boson field has a wave made from more than one quantum which are oscillating and moving in lock-step. But for fermions
Энергия одного кванта всё ещё равна h ν, так что всё обсуждение частиц и их энергий, импульса и масс остаётся в силе. Но количество квантов у электронной волны может равняться только 0 или 1. Десять электронов, в отличие от десяти фотонов, нельзя организовать в одну волну большей амплитуды. Поэтому не существует фермионных волн, состоящих из большого количества фермионов, колеблющихся и движущихся совместно.
Автор: SLY_G
