Вычисление коэффициентов прохождения и отражения для плоской волны, падающей на стопку пластин

в 11:57, , рубрики: diy или сделай сам, физика, фотонный кристалл, холестерики, метки: ,

Есть стопка стеклянных пластинок и захотелось нам построить для этой стопки частотную характеристику пропускания (или отражения) света. Вот как на рисунке: берем две стеклянные пластинки (отличаются показателем преломления) — строим; потом собираем стопочку из 10 пластин (те же два показателя преломления чередуются) — опять строим; а в конце делаем стопочку потолще (из 50 пластин) — и снова строим. Интересная же картинка: для толстой стопки есть интервал частот, которые совсем не проходят, Т=0, — вот эта стопка называется "одномерный фотонный кристалл". 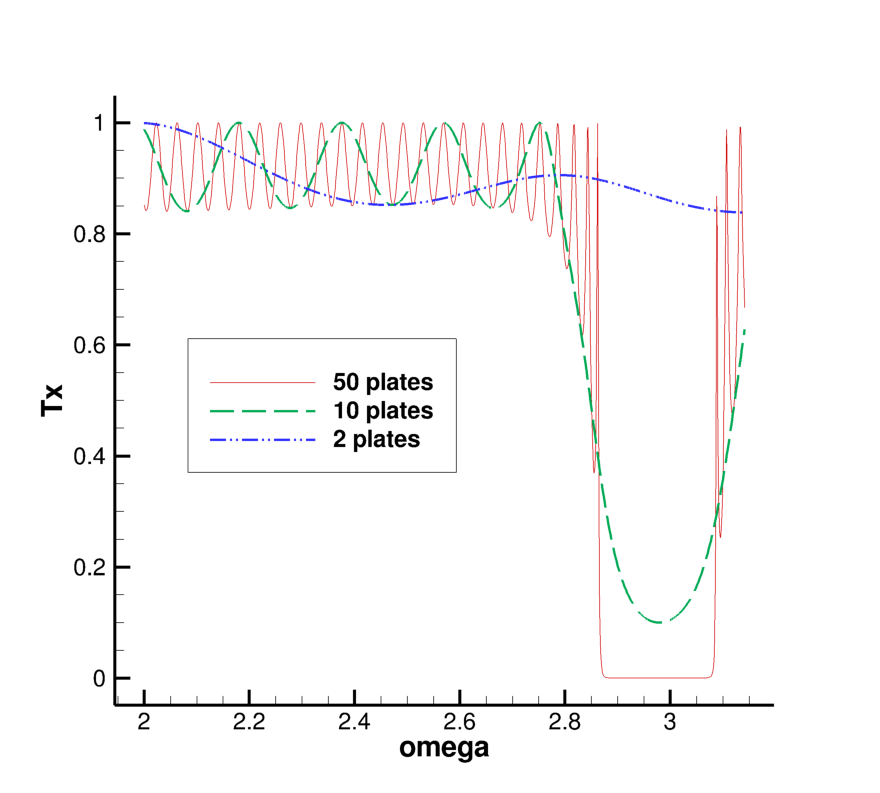Вычисление коэффициентов прохождения и отражения для плоской волны, падающей на стопку пластин - 1
Ну а как строить-то такую характеристику? А если пластинки поглощающие? А вдруг они еще и анизотропные некоторые? А если не просто анизотропные, а прям холестерические, как в жидкокристаллических мониторах? А если все они вообще разные и каждая со своим дихроизмом? Не беда!

Статья ориентирована на тех, кто захочет написать код функции, поэтому без математических выкладок — всё в стиле «делай, не думай».

Постановка задачи

Отрезок $z in [0,L]$ разделен на $n$ частей — «одномерных анизотропных пластин холестерического типа». Каждая пластина имеет свой собственный набор параметров: $varepsilon_{perp, i}$, $varepsilon_{parallel, i}$, $mu_{parallel, i}$, $mu_{perp, i}$, $q_i$, $varphi_{0, i}$, а также толщину $d_i>0:sum^{n}_{i=1}d_i=L$. Номера пластин упорядочены в порядке следования одной за другой слева направо (вдоль возрастания координаты $z$). Слева и справа от стопки анизотропных пластин находятся изотропные среды с параметрами: $varepsilon_{0},mu_{0}$ при $z<0$ и $varepsilon_{L},mu_{L}$ при $z>L$. Слева на стопку пластин падает плоская электромагнитная волна с частотой $omega$. Требуется найти коэффициент отражения $R$ и коэффициент пропускания $T$.

Задача решается в безразмерных величинах. Параметр обезразмеривания $r^*_{sgs}$ выбирается исходя из удобства. Безразмерные величины выражаются через размерные в системе $SGS$ следующим образом:

$vec{r}=vec{r}_{sgs}/r^*_{sgs},quad t=t_{sgs}cdot c_{sgs}/r^*_{sgs},quadomega=omega_{sgs}cdot r^*_{sgs}/c_{sgs},quadsigma=sigma_{sgs}cdot 4pi r^*_{sgs}/c_{sgs},quad q=q_{sgs}cdot r^*_{sgs}.$

При обезразмеривании вещественные части величин $varepsilon,, mu$ не изменяются.

1. Предварительные слова

1.1. Аргументы и возвращаемые значения функции

Аргументы (уже обезразмеренные)

$varepsilon_{0}$, $mu_{0} $ — диэлектрическая и магнитная проницаемости крайней левой изотропной среды (не обязательно вакуум, индекс значит $z=0$),
$varepsilon_{L}$, $mu_{L} $ — диэлектрическая и магнитная проницаемости крайней правой изотропной среды (индекс: $z=L$),
$omega $ — частота падающей волны,

Далее для каждого $i$-слоя (всего $nin N$ слоев):

$d_i>0$ — толщина слоя,
$q_i$ — пространственная частота холестерической спирали (может принимать отрицательные значения),
$varphi_{0, i}$ — «начальный» (какой он был бы при $z=0$, если спираль продолжить назад, — невзирая на истинную начальную координату $i$-слоя) угол между осью $O_x$ и вектором-директором $textbf{n}$ (см рис. ниже),
$varepsilon_{perp, i}$, $varepsilon_{parallel, i}$, $mu_{parallel, i}$, $mu_{perp, i}in C$ — в общем случае комплексные продольные и поперечные диэлектрические и магнитные проницаемости.

При этом мнимые части диэлектрических и магнитных проницаемостей отвечают за поглощение: $Im(varepsilon_{perp})=-{sigma_{perp}}/{omega}$, $Im(varepsilon_{parallel})=-{sigma_{parallel}}/{omega}$, $Im(mu_{perp})=-{sigma^*_{perp}}/{omega}$, $Im(mu_{parallel})=-{sigma^*_{parallel}}/{omega}$.
Вычисление коэффициентов прохождения и отражения для плоской волны, падающей на стопку пластин - 47

Возвращаемые значения

Всего рассматривается 4 типа падающих волн:

  • плоская поляризация по $x$,
  • плоская поляризация по $y$,
  • круговая поляризация правая $r$,
  • круговая поляризация левая $l$.

В соответствии с типом падающей волны, функция возвращает 4 коэффициента пропускания и 4 коэффициента отражения (всего 8 значений): $R_x, T_x, R_y, T_y, R_l, T_l, R_r, T_r$.

Коэффициенты определяются как доли энергии (отраженной, пропущенной) от энергии падающей волны.

При желании, долю поглощенной энергии $A$ в стопке можно вычислить по формуле: $A_{alpha}=1-(R_{alpha} + T_{alpha})$, где индекс $alpha$ обозначает тип падающей волны: $x,y,r,l$.

1.2. Используемые ниже обозначения

В основном действия состоят из вычисления и произведения комплексных матриц размерностью $4times4$.

Для обозначения каждой матрицы используется открывающая скобка, буква и закрывающая скобка. Например:$[z),~(beta},~{zrangle$. Открывающая и закрывающая скобки не всегда одинаковы. Обратные матрицы обозначаются обратным порядком скобок, например: ${zrangle:=langle z}^{-1}$. Буквой $z$ в скобках подчеркивается зависимость марицы от координаты. Если матрица не зависит от координаты, то в скобках присутствует другая буква. Таким образом, при обозначении матрицы, значение имеет уникальный набор скобок и их порядок следования.

Обозначения используются для лаконичности записи произведения матриц и удобства проверки правильности записи, выражаемого мнемоническим правилом: соседние перемножаемые матрицы должны иметь одинаковые граничащие скобки, что имеет смысл при переходе из одного пространства в другое. Эти-то 4-мерные пространства и обозначаются скобками: $]$ — пространство «неподвижное декартово», $)$ — пространство «вращающееся декартово», $}$ — пространство «собственных векторов», $rangle$ — пространство «количеств и направлений волн». Произведение матрицы на вектор интерпретируется как новое представление вектора: или в другом 4-пространстве, но при той же координате (если скобки матрицы отличаются) или в другой координате, но в том же 4-пространстве (если открывающя и закрывающая скобки одинаковы).

2. Вычислительные шаги

2.1. Вычисление собственных значений $lambda$

Для каждого слоя вычисляются 4 собственных значения по формуле:

$lambda=pm i sqrt{etapmtau},$

где

$eta=frac{omega^2}{2}(varepsilon_{perp}mu_{parallel}+varepsilon_{parallel}mu_{perp}) + q^2,$

$tau=sqrt{frac{omega^4}{4}(varepsilon_{perp}mu_{parallel}-varepsilon_{parallel}mu_{perp})^2 +omega^2 q^2(varepsilon_{perp}mu_{parallel}+varepsilon_{parallel}mu_{perp} + varepsilon_{perp}mu_{perp}+varepsilon_{parallel}mu_{parallel})}.$

Здесь $i$ — мнимая единица.

2.2. Вычисление собственных векторов $vec{beta}$

Каждому собственному значению $lambda$ соответствует собственный вектор $vec{beta}$: $(m)vec{beta}=lambdavec{beta}$, где

$(m) :=left ( begin{array}{cccc} 0 & q & 0 & -iomegamu_{perp}\ -q & 0 & iomegamu_{parallel} & 0\ 0 & iomegavarepsilon_{perp} & 0 & q\ -iomegavarepsilon_{parallel} & 0 & -q & 0 end{array} right ).$

Если $lambda$ кратности 2, то в этой задаче ему соответствует два собственных вектора.

2.3. Вычисление матрицы $[D_i]$

Для каждой $i$-слоя вычисляется матрица $[D_i]$. Нумерация слоев слева-направо, по возрастанию координаты $z$. Формула для вычисления:

$[D_i]=[z_l)(beta}{M_i}{beta)(z_r],$

где

${M_i}=left ( begin{array}{cccc} exp (-lambda_{1,i} d_i) & 0 & 0 & 0\ 0 & exp (-lambda_{2,i} d_i) & 0 & 0\ 0 & 0 & exp (-lambda_{3,i} d_i) & 0\ 0 & 0 & 0 & exp (-lambda_{4,i} d_i) end{array} right ),$

$(beta}:=left ( begin{array}{llll} begin{array}{c} {vdots}\ vec{beta}_1\ {vdots} end{array} & begin{array}{c} {vdots}\ vec{beta}_2\ {vdots} end{array} & begin{array}{c} {vdots}\ vec{beta}_3\ {vdots} end{array} & begin{array}{c} {vdots}\ vec{beta}_4\ {vdots} end{array} end{array} right ),$

$[z):=left ( begin{array}{cccc} cos (qz+varphi_0) & -sin (qz+varphi_0) & 0 & 0\ sin (qz+varphi_0) & cos (qz+varphi_0) & 0 & 0\ 0 & 0 & cos (qz+varphi_0) & -sin (qz+varphi_0)\ 0 & 0 & sin (qz+varphi_0) & cos (qz+varphi_0) end{array} right ),$

$(z]:=[z)^{-1}$, ${beta):=(beta}^{-1}$, $z_l,z_r$ — координаты соответсвенно левой и правой границы $i$-слоя: $z_r-z_l=d_i$.

2.4. Вычисление матрицы $[D]$

Формула для вычисления:

$[D]=[D_1]dots [D_{n-1}][D_n].$

2.5. Вычисление матрицы $langle Urangle $

Формула для вычисления:

$langle Urangle=langle 0][D][Lrangle,$

где

$begin{array}{c} displaystyle [Lrangle=left ( begin{array}{cccc} e^{-iomegarho_L L} & 0 & e^{iomegarho_L L} & 0\ 0 & e^{-iomegarho_L L} & 0 & e^{iomegarho_L L} \ 0 & -e^{-iomegarho_L L}cdotrho_L/mu_L & 0 & e^{iomegarho_L L}cdotrho_L/mu_L \ e^{-iomegarho_L L}cdotrho_L/mu_L & 0 & -e^{iomegarho_L L}cdotrho_L/mu_L & 0 end{array} right ),\ displaystyle langle 0]=frac{1}{2} left ( begin{array}{cccc} 1 & 0 & 0 & mu_0/rho_0 \ 0 & 1 & -mu_0/rho_0 & 0\ 1 & 0 & 0 & -mu_0/rho_0 \ 0 & 1 & mu_0/rho_0 & 0 end{array} right ), end{array} $

при $rho_L=sqrt{varepsilon_Lmu_L}$, $rho_0=sqrt{varepsilon_0mu_0}$.

2.6. Вычисление векторов $textbf{c} $

Предварительные вычисления. Если

$langle Urangle=left ( begin{array}{cccc} u_{11} & u_{12} & u_{13} & u_{14}\ u_{21} & u_{22} & u_{23} & u_{24}\ u_{31} & u_{32} & u_{33} & u_{34}\ u_{41} & u_{42} & u_{43} & u_{44} end{array} right ),$

то вычисляются:

$T:=left ( begin{array}{cc} u_{11} & u_{12}\ u_{21} & u_{22} end{array} right )^{-1}=left ( begin{array}{cc} t_{11} & t_{12}\ t_{21} & t_{22} end{array} right ),$

$R:=left ( begin{array}{cc} u_{31} & u_{32}\ u_{41} & u_{42} end{array} right ) left ( begin{array}{cc} t_{11} & t_{12}\ t_{21} & t_{22} end{array} right )=left ( begin{array}{cc} r_{11} & r_{12}\ r_{21} & r_{22} end{array} right ).$

Теперь векторы $textbf{c} $ записываются:

$textbf{c}_{x,I}=left ( begin{array}{c} 1\ 0\ 0\ 0 end{array} right ),quad textbf{c}_{x,R}=left ( begin{array}{c} 0\ 0\ r_{11}\ r_{21} end{array} right ),quad textbf{c}_{x,T}=left ( begin{array}{c} t_{11}\ t_{21}\ 0 \ 0 end{array} right ), $

$textbf{c}_{y,I}=left ( begin{array}{c} 0\ 1\ 0\ 0 end{array} right ),quad textbf{c}_{y,R}=left ( begin{array}{c} 0\ 0\ r_{12}\ r_{22} end{array} right ),quad textbf{c}_{y,T}=left ( begin{array}{c} t_{12}\ t_{22}\ 0\ 0 end{array} right ).$

2.7. Вычисление векторов $textbf{a} $

Плоская поляризация Формулы для вычисления:

$textbf{a}_{x,I}=[0rangletextbf{c}_{x,I},quad textbf{a}_{x,R}=[0rangletextbf{c}_{x,R},quad textbf{a}_{x,T}=[Lrangletextbf{c}_{x,T}.$

$textbf{a}_{y,I}=[0rangletextbf{c}_{y,I},quad textbf{a}_{y,R}=[0rangletextbf{c}_{y,R},quad textbf{a}_{y,T}=[Lrangletextbf{c}_{y,T}.$

Здесь

$ [Lrangle=left ( begin{array}{cccc} e^{-iomegarho_L L} & 0 & e^{iomegarho_L L} & 0\ 0 & e^{-iomegarho_L L} & 0 & e^{iomegarho_L L} \ 0 & -e^{-iomegarho_L L}cdotrho_L/mu_L & 0 & e^{iomegarho_L L}cdotrho_L/mu_L \ e^{-iomegarho_L L}cdotrho_L/mu_L & 0 & -e^{iomegarho_L L}cdotrho_L/mu_L & 0 end{array} right ),$

$[0rangle=langle 0]^{-1}=left ( begin{array}{cccc} 1 & 0 & 1 & 0\ 0 & 1 & 0 & 1 \ 0 & -rho_0/mu_0 & 0 & rho_0/mu_0 \ rho_0/mu_0 & 0 & -rho_0/mu_0 & 0 end{array} right ),$

при $rho_L=sqrt{varepsilon_Lmu_L}$, $rho_0=sqrt{varepsilon_0mu_0}$.

Круговая поляризация Формулы для вычисления:

$textbf{a}_{r,I}=textbf{a}_{x,I}+itextbf{a}_{y,I},quad textbf{a}_{r,R}=textbf{a}_{x,R}+itextbf{a}_{y,R},quad textbf{a}_{r,T}=textbf{a}_{x,T}+itextbf{a}_{y,T}.$

$textbf{a}_{l,I}=textbf{a}_{x,I}-itextbf{a}_{y,I},quad textbf{a}_{l,R}=textbf{a}_{x,R}-itextbf{a}_{y,R},quad textbf{a}_{l,T}=textbf{a}_{x,T}-itextbf{a}_{y,T}.$

2.8. Вычисление коэффициента отражения $R$ и коэффициента прохождения $T$

Вектор $textbf{a}$ имеет структуру:

$textbf{a} :=left ( begin{array}{c} e_x\ e_y\ h_x\ h_y end{array} right ),$

Плотность потока энергии определяется $langletextbf{S}rangle$ — вектором Пойнтинга, усредненным по периоду колебаний:

$leftlangle textbf{S}(t)rightrangle=leftlangleoperatorname{Re}[textbf{E}] times operatorname{Re}[textbf{H}]rightrangle=frac{1}{4}left( textbf{e} times textbf{h}^*+textbf{e}^* times textbf{h} right), $

где звездочкой ${}^*$ обозначено комплексное сопряжение.

Используя эту формулу вычисляются

$begin{array}{c} displaystyle langletextbf{S}rangle_{I,alpha}:=langletextbf{S}rangle(textbf{a}_{alpha,I}),\ displaystyle langletextbf{S}rangle_{T,alpha}:=langletextbf{S}rangle(textbf{a}_{alpha,T}),\ displaystyle langletextbf{S}rangle_{R,alpha}:=langletextbf{S}rangle(textbf{a}_{alpha,R}), end{array}$

где $alpha$ принимает значения $x,y$ (падают волны плоской поляризации) либо $r,l$ (падают волны круговой поляризации).

Для нахождения коэффициента отражения $R$ и коэффициента прохождения $T$ используются формулы:

$T_{alpha}=frac{|langletextbf{S}rangle_{T,alpha}|}{| langletextbf{S}rangle_{I,alpha}|}, quad R_{alpha}=frac{|langletextbf{S}rangle_{R,alpha}|}{| langletextbf{S}rangle_{I,alpha}|}.$

3. Заключение

Ну вот. Теперь можно применять. Инструмент забавный. Всем добра.

Автор: FransuaMaryDelone

Источник

* - обязательные к заполнению поля

Рейтинг@Mail.ru
Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js