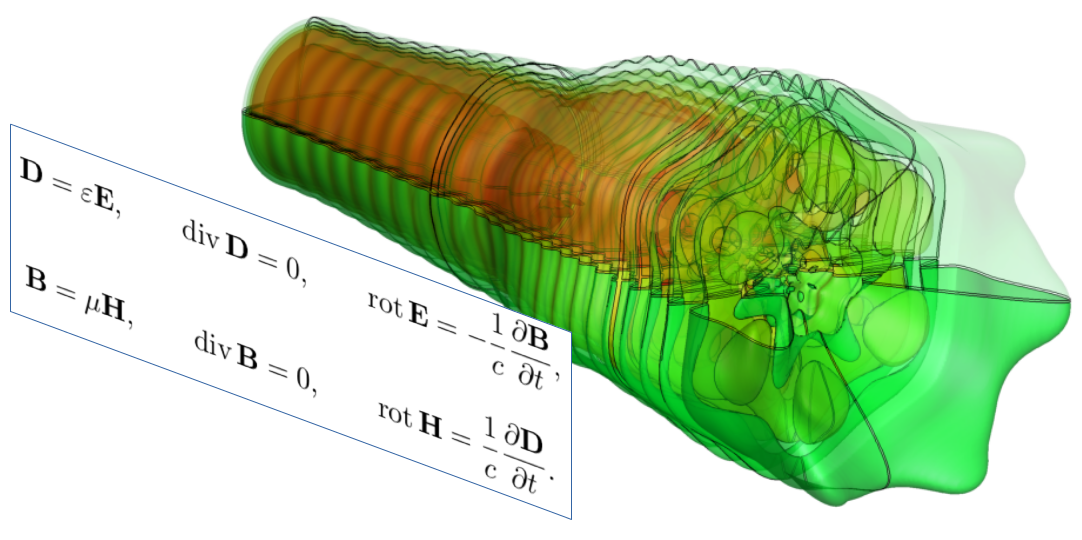
Как-то мне понадобилась "собственная мода оптоволокна". Но я нигде не нашел аналитического выражения электромагнитного поля. Ну и «сделал сам», раз не нашел, и оформил для всех тут, в статье. Так что, скорее всего, нигде больше вы такого не встретите — уникальнейшая вещь! В книжках это не пишут, потому что оно длинное — обычно пишут самое простое, а про общий случай упоминают вскользь. Ну вот он, общий случай, под катом.
Постановка задачи
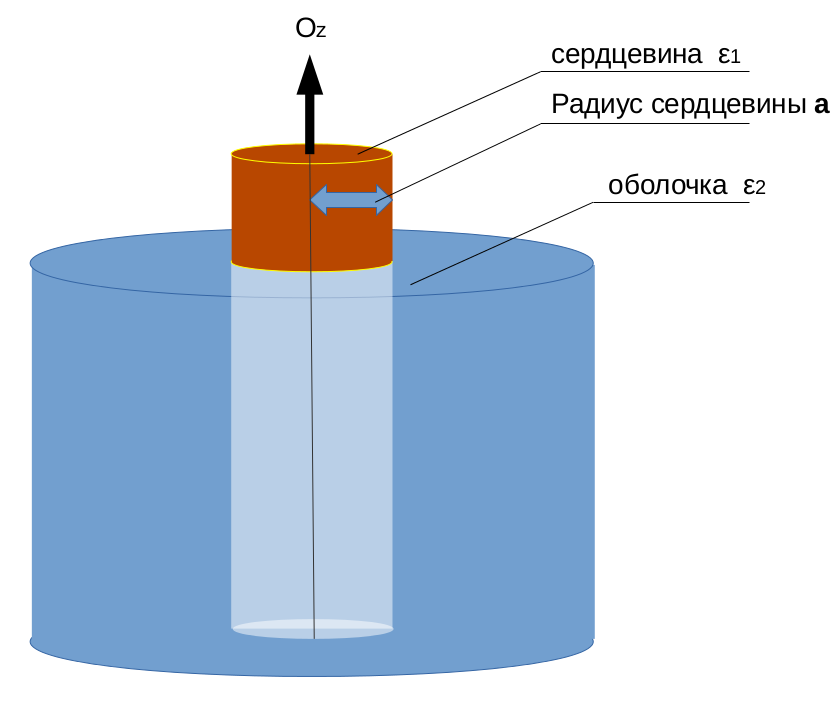
Решить уравнения Максвелла с условиями:
— оптоволокно состоит из сердцевины радиуса 


— поле периодично по 

— компоненты поля на оси 
— компоненты поля при 
— тангенциальные компоненты поля на поверхности цилиндра 

1. Преобразование уравнений Максвелла, вызванное периодичностью по 
Подставив в уравнения Максвелла периодическую зависимость по 
получаются уравнения на 
При этом остальные компоненты выражаются через 
где 



2. Уравнения на  -компоненты в полярных координатах
-компоненты в полярных координатах
Уравнения на 

В полярных координатах уравнение имеет вид:
3. Разделение переменных в уравнении
Подстановкой в уравнение зависимости 
Обозначив константу равенства символом 
$$display$$- frac{1}{v(varphi)}frac{partial^2 }{partial varphi^2}v(varphi) = nu^2,$$display$$
4. Решение первого уравнения
Первое уравнение имеет решения: 
Из периодического граничного условия 


5. Решение второго уравнения
Второе уравнение сводится либо к уравнению Бесселя, либо к модифицированному уравнению Бесселя:
1. Уравнение Бесселя:
2. Модифицированное уравнение Бесселя:
Уравнению Бесселя удовлетворяют функции Бесселя 



В силу граничных условий: при 






Из предложенной комбинации следует, что сердцевина должна быть более оптически плотной, чем оболочка, 
6. Общий вид компонент 
Введя обозначения: 

Здесь полагается, что 

Кроме того, введен индекс для магнитной проницаемости: 

7. Соотношения на константы 
Используя закон
находятся компоненты 

Компоненты подставляются в граничное условие непрерывности тангенциальных компонент:
Получается система линейных уравнений, суть соотношения на константы 
8. Дисперсионное соотношение
Для существования нетривиального решения системы линейных уравнений, определитель матрицы должен равняться нулю:
В этой записи нулевого детерминанта использованы обозначения: 



Величины 

9. Моды
Для нахождения 
необходимо задать: 
Связь 


Связь 


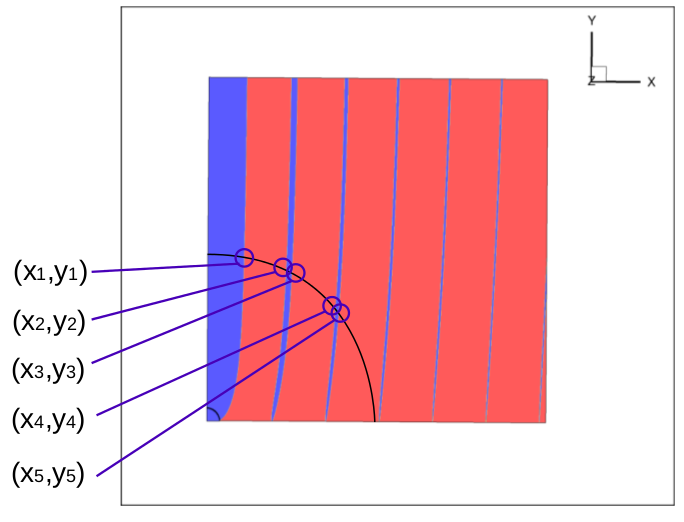
Набор решений составляет конечное число пар чисел 
Моду оптоволокна принято обозначать следующим образом: две буквы (


Примеры обозначения:










10. Порядок построения компонент поля
Подготовительные вычисления:
01. Задать 
02. Найти наборы 
03. Вычислить 
04. Вычислить 
Выражения в цилиндрических координатах компонент поля:
Далее, при 
При 
Далее
При этом замыкающие соотношения стандартные:
Выражение поля в декартовой системе координат через цилиндрические для электрических компонент:
Для магнитных компонент матрица та же.
11. Замечания
Выбирая 
Такое оптоволокно называется одномодовым. Однако следует заметить, что «одномодовость» зависит от частоты — более высокие частоты распространяются в «одномодовом» волокне в виде набора мод.
Иногда говорят о сохранении поляризации в оптоволокне, имея в виду перпендикулярные компоненты поля моды 
Для интереса ниже показана эволюция в течении временного периода моды
и моды
Автор: FransuaMaryDelone






![Аналитическое решение уравнений Максвелла: собственные моды оптоволокна (любителям «матана») - 21 $textbf{b}_{bot}=frac{i}{gamma^2}leftlbrace k_z operatorname{grad}_{bot}b_z + varepsilonmufrac{omega}{c}left[ hat{textbf{z}}timesoperatorname{grad}_{bot}e_zright] rightrbrace, , textbf{e}_{bot}=frac{i}{gamma^2}leftlbrace k_z operatorname{grad}_{bot}e_z - frac{omega}{c}left[ hat{textbf{z}}timesoperatorname{grad}_{bot}b_zright] rightrbrace,$](https://www.pvsm.ru/images/2017/04/12/analiticheskoe-reshenie-uravnenii-maksvella-sobstvennye-mody-optovolokna-lyubitelyam-matana-21.svg)














![Аналитическое решение уравнений Максвелла: собственные моды оптоволокна (любителям «матана») - 69 $textbf{b}_{bot}=frac{i}{gamma^2}leftlbrace k_z operatorname{grad}_{bot}b_z + varepsilonmufrac{omega}{c}left[ hat{textbf{z}}timesoperatorname{grad}_{bot}e_zright] rightrbrace, , textbf{e}_{bot}=frac{i}{gamma^2}leftlbrace k_z operatorname{grad}_{bot}e_z - frac{omega}{c}left[ hat{textbf{z}}timesoperatorname{grad}_{bot}b_zright] rightrbrace,$](https://www.pvsm.ru/images/2017/04/12/analiticheskoe-reshenie-uravnenii-maksvella-sobstvennye-mody-optovolokna-lyubitelyam-matana-69.svg)





![Аналитическое решение уравнений Максвелла: собственные моды оптоволокна (любителям «матана») - 78 $left( frac{varepsilon_1mu_1}{x^2}+frac{varepsilon_2mu_2}{y^2}right) left( frac{1}{x^2} + frac{1}{y^2}right)nu^2=left[ mu_2 g(y)+mu_1 f(x)right] left[ varepsilon_2g(y) + varepsilon_1 f(x)right] .$](https://www.pvsm.ru/images/2017/04/12/analiticheskoe-reshenie-uravnenii-maksvella-sobstvennye-mody-optovolokna-lyubitelyam-matana-78.svg)

![Аналитическое решение уравнений Максвелла: собственные моды оптоволокна (любителям «матана») - 87 $left( frac{varepsilon_1mu_1}{x^2}+frac{varepsilon_2mu_2}{y^2}right) left( frac{1}{x^2} + frac{1}{y^2}right)nu^2=left[ mu_2 g(y)+mu_1 f(x)right] left[ varepsilon_2g(y) + varepsilon_1 f(x)right],$](https://www.pvsm.ru/images/2017/04/12/analiticheskoe-reshenie-uravnenii-maksvella-sobstvennye-mody-optovolokna-lyubitelyam-matana-87.svg)


















