Запутанная квантовая физика

Феномен квантовой запутанности (entanglement), когда разделенные в пространстве частицы мистическим образом взаимодействуют друг с другом, нахально нарушая запрет на передачу взаимодействий со сверхсветовой скоростью, давно считается частью науки и у научного сообщества не вызывает никаких сомнений. Вполне серьезно изучаются перспективы создания на этой основе квантовых компьютеров. Считается, что их элементы данных — кубиты будут изменять и передавать свое информационное состояние посредством механизма квантовой запутанности. Такая прагматичная организация, как DARPA щедро финансирует эту чудесную науку. А между тем имеет серьезные основания точка зрения, согласно которой квантовая запутанность в смысле парадокса ЭПР — это миф, который прижился в поверхностном слое понимания квантовой механики.

Парадокс ЭПР

Эйнштейн предпринял атаку на квантовую механику со знаменем в руках, на котором было написано «Бог не играет в кости». В знаменитой статье [0], опубликованной в 1935-м, появился т.н. парадокс ЭПР (Эйнштейна, Подольского, Розена). Из этого парадокса, который на самом деле является софизмом, родился миф о квантовой запутанности.

Основная идея ЭПР, согласно статье его авторов, выглядит следующим образом. Пусть имеется пара квантовых объектов 1 и 2, образующих единую систему с волновой функцией , где наборы переменных и используются для описания поведения подсистем 1 и 2 в отдельности. Если задан полный набор собственных волновых функций для некоторых наблюдаемых системы 1, то функция разлагается в ряд Фурье:

Теперь предположим, что подсистемы удаляются друг от друга и через некоторое время расстояние между ними стало настолько большим, что взаимное влияние невозможно. Если затем измерить значения (коммутирующих) наблюдаемых системы 1, то, в силу принципов квантовой механики, она скачком перейдет в некоторое собственное состояние . В контексте запутанной парадигмы это событие имеет драматическое название «коллапс волновой функции». Следовательно, рассуждают далее авторы ЭПР, вся система в целом скачком переходит в состояние c волновой функцией . Это означает, что подсистема 2 внезапно оказалась в состоянии , хотя никакого воздействия подсистемы 1 и измерительных приборов на нее не было.

Перед нами главный эффект, с которым связано представление о нелокальности квантовой механики, а именно — непонятное и необъяснимое, мгновенное взаимодействие удаленных квантовых объектов 1 и 2. Оно заключается в том, что при измерении некоторых физических величин, связанных с системой 1, автоматически и сразу меняется состояние системы 2.

В приведенных рассуждениях есть сразу две ошибки. Первая заключается в том, что волновая функция , вообще говоря, не отвечает собственному состоянию объединенной системы. Поэтому последняя не обязана переходить в скачком при измерении, связанном только с системой 1. И все же возникает вопрос: в каком состоянии окажется подсистема 2 после измерения 1? Ответ прост и очевиден — ее состояние не изменится. В самом деле, поскольку в рассматриваемой ситуации объекты 1 и 2 независимы, то

где — волновая функция системы , рассматриваемой в отдельности. Следовательно, как только подсистема 1 оказалась в собственном состоянии , подсистема 2 автоматически оказывается в… своем исходном состоянии . Что и следовало ожидать!

Вторая ошибка заключается в том, что пара не взаимодействующих объектов 1 и 2, формально объединенных в единую систему, на самом деле не испытывает возмущения при измерении, которое связано лишь с подсистемой 1. Такое «возмущение» не способно вызвать скачок объединенной системы в одно из собственных состояний (полного набора коммутирующих наблюдаемых, полученного объединением наборов 1 и 2). Для этого нужно было бы возмутить всю систему в целом, т.е., реально подействовать также и на объект 2.

Таким образом, псевдопарадокс ЭПР лишь вынуждает нас уточнить понятие возмущения. Но вместо этого ему придают абсолютный и формальный смысл, как если бы взмах крыла бабочки считался возмущением Вселенной,… хотя с философской точки зрения так оно и есть. Выше дан точный ответ на вопрос, что именно происходит с подсистемой 2 после измерения 1. По существу ничего!

Из своего псевдопарадокса авторы ЭПР сделали далеко идущие выводы о неполноте квантовой механики, т.е. о том, что эта теория нуждается в дополнительных параметрах для описания квантовых систем. Параметрах, которые исключают всякую неопределенность и делают их поведение детерминированным в классическом духе. С точки зрения Эйнштейна наука пока просто не знает этих скрытых параметров и законов их поведения, поэтому ограничивается вероятностным характером квантовых прогнозов.

В популярных объяснениях эффекта квантовой запутанности пары частиц, после вольного изложения ЭПР всегда ссылаются на законы сохранения. Рассмотрим случай пары электронов. Рассуждать о сохранении импульса нет смысла, хотя часто приводится пример пары «запутанных» электронов с импульсами . Поскольку оператор импульса имеет непрерывный спектр, его собственные состояния практически не могут быть реализованы. Поэтому на квантовом уровне бессмысленно рассматривать пару электронов с импульсами . Таким образом, отбросим импульс в сторону и рассмотрим случай «запутанной» пары электронов с нулевой суммарной проекцией спина на ось Z (синглет).

Сохранение проекции спина означает, что для оператора проекции спина на ось Z имеет место , где — оператор энергии данной системы. В частности это означает, что если система первоначально находится в собственном состоянии оператора , то в дальнейшем, при отсутствии внешних возмущений она будет при каждом находиться в собственном состоянии наблюдаемой , хотя вектор состояния может изменяться во времени.

Для единственного электрона оператор имеет два собственных вектора, обозначим их и , так что

Предположим, что пара электронов первоначально находится в состоянии , где — любое комплексное число. Здесь вектор отвечает такому состоянию пары, что первый электрон находится в состоянии , а второй в состоянии . Состояние является собственным для спина системы из двух электронов, поэтому при измерении система останется в этом состоянии и будет получено нулевое значение для спина пары.

В процессе разбегания электронов в разные стороны спиновое состояние синглета не изменится, если система остается изолированной вплоть до момента первого измерения. Это означает, что при каждом пара электронов находится в состоянии , которое является собственным для оператора и отвечает собственному значению . Согласно популярным рассуждениям о паре запутанных электронов, при измерении спина одной из частиц произойдет скачок системы в собственное состояние оператора . Но согласно квантовой механике, поскольку система уже находится в собственном состоянии (полного набора коммутирующих наблюдаемых, включающего , она останется в нем после измерения. Соответственно, изменится разве лишь числовой множитель перед вектором .

Таким образом, перехода измеряемого электрона в состояние , а второго в состояние не произойдет. Получено противоречие с тем фактом, что измеряемый электрон все-таки перейдет в собственное состояние своего оператора . Отсюда следует, что при измерении спина одного из электронов совместное состояние синглета будет разрушено. При этом состояние второго электрона останется неизменным, т.е., неопределенным с точки зрения спина, а именно .

В рамках запутанной парадигмы также рассматривают пару фотонов в одинаковых состояниях поляризации, так что общее состояние пары можно задать вектором , где и задают состояния поляризации в перпендикулярных направлениях. Если при измерении одного из фотонов он перейдет в собственное состояние , то якобы это повлечет переход пары в состояние , т.е., мгновенный скачок второго фотона в такое же состояние поляризации . Однако, аналогично примеру с синглетом электронов можно утверждать, что пара фотонов останется в собственном состоянии . Это противоречие означает, что измерение одного из двух фотонов разрушает систему, после чего второй фотон остается в исходном состоянии . Запутанности в смысле ЭПР и здесь не возникает.

Неравенства Белла

В 1964 Джон Стюарт Белл написал интересную статью , в которой подверг критическому анализу гипотезу о скрытых параметрах. Эти, на удивление простые рассуждения Белла оказали большое влияние на развитие квантовой физики с конца XX века по настоящее время.

По ходу своих рассуждений Белл вывел неравенство , где — это единичные векторы различных направлений в пространстве, на которые проектируются спины двух разбегающихся в разные стороны частиц (электронов). Изначально частицы имеют нулевой суммарный спин, т.е. образуют синглет. При этом обозначает ненормированный коэффициент корреляции пары случайных величин и , являющихся проекциями спиновых переменных и частиц 1 и 2 на направления векторов и соответственно. Другими словами — это среднее значение произведения чисел и . Которые, заметим, принимают значения . Данное неравенство имеет место при условии, что верна гипотеза Эйнштейна о скрытых параметрах квантовой системы. И оно может быть проверено статистически. В дальнейшем были аналогично получены другие неравенства, которые применимы не только к синглетной паре электронов, и все они называются неравенствами Белла. Например такое:

Оно также справедливо лишь в том случае, если есть скрытые параметры квантовой системы, определяющие ее поведение. При этом, поскольку законы поведения этих параметров неизвестны, они считаются случайными величинами.

Для иллюстрации последнего утверждения, рассмотрим опыт с бросанием монеты. Понятно, что полет брошенной монеты определяется многими величинами, которые описывают ее форму, распределение массы, детальные условия броска, форму поверхности падения и другие факторы, от которых зависит ответ на вопрос: «орел или решка». При полном учете всех этих «скрытых параметров», которые Белл обозначает символом , можно было бы дать 100% надежный прогноз того, как именно упадет монета. Однако такой учет слишком сложен, и в этом нет большой необходимости, поэтому довольствуются вероятностным прогнозом того, как упадет монета. Соответственно, скрытые параметры следует считать случайными величинами. Вопрос: существуют ли аналогично скрытые параметры у любой квантовой системы, или же таких параметров нет, а стохастическое поведение субатомных объектов заложено в природе вещей?

В экспериментах с т.н. запутанными частицами, чаще всего фотонами, искомым результатом всегда является нарушение неравенства Белла. Такие нарушения в самом деле наблюдаются с конца 70-х годов прошлого века, и сегодня принято толковать их, как доказательства возникновения запутанных квантовых состояний. При этом значительные усилия экспериментаторов направлены на то, чтобы разнести на возможно большие расстояния приборы, которые регистрируют спины частиц или направления поляризации фотонов, чтобы исключить взаимное влияние объектов и приборов измерения. Сделав тем самым максимально убедительным эффект мгновенной передачи взаимодействий, положенный в основу фантазий о квантовой телепортации.

Однако в действительности, нарушение неравенств Белла означает одно из двух.

a) У квантовых систем нет скрытых параметров. Это полностью соответствует квантовой механике и не связано с запутанностью.

b) Скрытые параметры есть и тогда измерения одной из подсистем могут влиять на другую. Поэтому квантовая запутанность имеет место быть.

Соответственно нет оснований утверждать, что нарушения неравенств Белла экспериментально доказывают феномен ЭПР — запутанности. Разумно предположить, что они влекут за собой a), т.е., что квантовая механика не нуждается в скрытых параметрах и апгрейде в духе Бома. Однако, принято считать эти нарушения свидетельствами ЭПР — запутанности фотонных пар.

Данная парадигма сформировалась под влиянием работ Аспэ и других ученых, поставивших аналогичные эксперименты. Помимо несомненных нарушений неравенств Белла, в них якобы наблюдались корреляции между направлениями поляризации взаимно удаленных фотонов. Будь это так, для опытной проверки ЭПР — запутанности в неравенствах Белла не было бы необходимости. Стоит заметить, что сам Аспэ, судя по статье [1], считал свидетельством запутанности только корреляции. Но в действительности наблюдалась «корреляция» каждого фотона, попавшего в фотоумножитель, с самим собой. Точнее: он достигал двух фотоумножителей почти одновременно (см. ниже).

Опыт Аспэ

Опыт Алана Аспэ (Aspect) — блестящего экспериментатора и классика квантовой магии, внес основной вклад в трансформацию ЭПР — мифа в догму. Результаты опытов Аспэ и других были интерпретированы на основе представления о фотонах, как точечных частицах (с обычными оговорками о корпускулярно-волновом дуализме). Оно является ошибочным, т.к. у фотона нет представления Шредингера [2]. Говоря простым языком, для этих частиц понятие пространственных координат лишено смысла. Поэтому нельзя говорить о том, что в определенный момент времени фотон находится в определенном месте. Он может быть локализован в состоянии малого волнового пакета, но в этом случае поляризация теряет смысл.

В связи с этим уместно процитировать Дирака (P.A.M. Dirac, стр. 25 [2]).

"… Пусть мы имеем пучок света, состоящий из большого числа фотонов, который расщепляется на две компоненты одинаковой интенсивности. Сделав предположение о том, что интенсивность пучка связана с вероятным числом фотонов, мы получили бы, что в каждую из компонент попала бы половина от общего числа фотонов. Если далее эти две компоненты будут интерферировать, то мы должны потребовать, чтобы фотон из одной компоненты мог интерферировать с фотоном в другой компоненте. Иногда эти два фотона уничтожались бы, иногда же они превращались бы в четыре фотона. Это противоречило бы закону сохранения энергии. Новая теория, которая связывает волновую функцию с вероятностями для одного фотона, преодолевает эту трудность, считая, что каждый фотон входит отчасти в каждую из двух компонент. Тогда каждый фотон интерферирует лишь с самим собой. Интерференции между двумя разными фотонами никогда не происходит."

Аналогичная мысль звучит в цитате из Гейзенберга, которая касается парадокса ЭПР и имеет отношение к интерпретации опытов Аспэ (W. Heisenberg, стр. 34 [3]).

"В связи с этими рассуждениями здесь должно быть указано на мысленный эксперимент, предложенный Эйнштейном. Вообразим один световой квант, который представлен посредством волнового пакета, построенного из максвеллевских волн и которому, таким образом, приписана известная область пространства и, в смысле соотношений неопределенности, также определенная область частот. Посредством отражения от полупрозрачной пластинки мы можем очевидно легко разложить этот волновой пакет на две части: отраженную и прошедшую. Тогда существует определенная вероятность найти световой квант или в одной, или в другой части волнового пакета. Через достаточно долгое время обе части будут сколько угодно далеко удалены друг от друга. Если теперь посредством опыта будет установлено, что световой квант находится, положим, в отраженной части волнового пакета, то это одновременно даст, что вероятность нахождения светового кванта в другой части равна нулю. Опыт на месте отраженной половины пакета производит тем самым некоторое действие (сведение волнового пакета!) на сколь угодно удаленном расстоянии, где находится другая половина, и легко видеть, что это действие распространяется со сверхсветовой скоростью."

Таким образом, попытки обнаружить ЭПР — запутанные пары фотонов с помощью интерферометра лишены смысла. Допустим, мы разделили световой луч полупрозрачным зеркалом, после чего пропустили один пучок через поляризатор. Согласно парадигме ЭПР, возникают запутанные пары одинаково поляризованных фотонов из двух пучков. Это может быть проверено через интерференцию, но так как интерферировать каждый фотон будет с самим собой, совпадение измеренных в разных местах поляризаций не может быть истолковано, как ЭПР — запутанность.

Неявно предполагаемая возможность поляризации точечного фотона легла в основу ложной интерпретации опытов Аспэ. Начнем с краткого описания этих экспериментов (подробности в статье [1]).

Использовались флуоресцентные источники каскадного излучения, где атомы испускают пары квантов с интервалом нс. В первых опытах один из фотонов пары имел длину волны 551.3 нм (зеленый свет), а другой 422.7 нм (фиолетовый). Исходя из законов сохранения импульса и момента импульса считается, что в каждом каскаде фотоны разлетаются в разные стороны, имея одинаковые направления круговой поляризации — левое или правое с вероятностями 0.5, что равносильно пребыванию в суперпозиции двух состояний линейной поляризации в направлениях осей X и Y. Как полагают Аспэ и его последователи, эта пара квантов света рождается в запутанном, поляризационном состоянии:

Состояния , отвечают направлениям поляризации вдоль осей координат, состояния , — двум направлениям круговой поляризации фотона номер .

ЭПР — запутанность означает, что если один из фотонов будет обнаружен поляризованным вдоль оси X (для чего достаточно пропустить его через поляризатор с X — ориентацией), то второй автоматически, в то же мгновение окажется в том же состоянии (что можно обнаружить с помощью второго поляризатора). То же самое в отношении оси Y. В этом случае говорят о корреляции между направлениями поляризации фотонов запутанной пары, которую можно измерить.

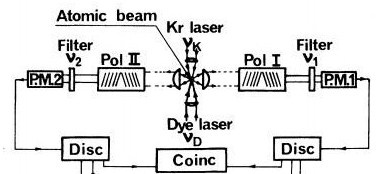
Схема опыта Аспэ

На схеме пара лазеров возбуждает флуоресцентный источник каскадного излучения, который, по мысли Аспэ, излучает пары запутанных фотонов. Каждый из них проходит через свой поляризатор (Pol I и Pol II), после чего, пройдя через частотный фильтр, попадает в фотоумножитель (PM I и PM II). Последний, по существу, является детектором одиночных фотонов и работает по принципу электронной лавины, которую инициирует фотоэффект. Схема управления фотоумножителями организована так, что каждая пара квантов детектируется во временном окне около 20 нс. Попадание в него случайной пары фотонов от двух разных атомов маловероятно. Таким образом, схема почти наверняка зафиксирует только пару, излученную в одном каскаде. Происходит это в среднем 100 раз в секунду. Напомним, что каждая такая пара считается ЭПР — запутанной.

Если теперь за некоторый период времени подсчитать числа пар для случаев, когда один из поляризаторов («левый» или «правый») удален, то можно вычислить коэффициент корреляции между событиями поляризованности левого фотона в заданном направлении , а правого в направлении . Такие измерения позволяют проверить неравенства Белла, а также выявляют корреляцию между поляризациями фотонов каждой пары (для различных направлений и ). Именно это было сделано группой Аспэ.

Однако, в опыте Аспэ мог иметь место подсчет одиночных фотонов, которые достигали двух фотоумножителей в виде волн со сферическими фронтами (волновыми поверхностями). Согласно квантовой электродинамике [4], поле фотона с заданным моментом импульса распространяется именно в виде такой волны. Можно доказать, что эта волна приходит к каждому из двух поляризаторов в одинаковых фазах, хотя и в разные моменты времени в силу различной удаленности от излучателя. При этом угол между вектором напряженности поля и осью каждого поляризатора один и тот же для любой волновой поверхности. Поэтому волна одного фотона взаимодействует с двумя поляризаторами одинаково. Это и создает иллюзию пары частиц, запутанных в поляризациях.

На сказанное можно возразить, что счетчик фотонов срабатывает дважды в среднем через нс, как и должно быть при излучении каскадов. Однако, время срабатывания фотоумножителя элементарно оценивается нс. В течение этого времени может быть зафиксирован только один фотон. В действительности он является волновым пакетом, центрированным на сфере . Если размер пакета м, что отвечает допплеровскому уширению спектральной линии , то время прохождения через фотоумножитель имеет порядок интервала между фотонами одного каскада. В условиях опытов Аспэ такое уширение было возможно. Таким образом, до срабатывания пары фотоумножителей на первом фотоне второй не мог быть детектирован, а к моменту, когда оба устройства готовы принять второй фотон, его пакет уже прошел. По-видимому, в большинстве случаев пара фотоумножителей фиксировала только один из двух фотонов каждого каскада.

Заметим также, что в рассматриваемом состоянии направление движения фотона не определено. Это связано с тем, что импульс и его момент не коммутируют. Следовательно, аналогии с классической механикой, которые используются в качестве причины запутанного состояния пары фотонов, в данном случае неуместны. Кроме того, излучение фотона сопровождается возмущением. После него атом окажется не в состоянии с нулевым моментом, а в суперпозиции собственных состояний момента. Таким образом, законы сохранения не влекут состояние пары фотонов одного каскада вида

За время излучения расстояние между фотонами пары составит м. Идея о том, что такая пара рождается запутанной, противоречит здравому смыслу. Впрочем, последнее относится ко всей квантовой магии.

Таким образом, результаты опытов Аспэ имеют интерпретацию, которая не связана с ЭПР — запутанностью. Необходимы более точные оценки, но уже есть основания предполагать, что в этих экспериментах совместные, ЭПР — запутанные состояния не наблюдались. По-видимому, подобным образом можно объяснить все опыты с т.н. запутанными фотонами.

Представления о запутанных состояниях взаимно удаленных частиц, восходящие к парадоксу ЭПР, широко популяризованы и уже считаются частью квантовой механики. Одной из целей данной статьи было показать, что фундамента под этим нет. Мыльный пузырь на иллюстрации символизирует волновой фронт фотона с заданным угловым моментом, а также теорию квантовых компьютеров, основанную на ЭПР — запутанности.

Автор: SpaceOdyssey

Источник