Есть очень много научно-популярных статей и книг о гравитации, в которых рассказывается об искривлении пространства-времени и приводятся картинки с продавленной простыней (батутом, матом). Давайте вместе сломаем этот порядок вещей! Под катом вас ждёт вполне себе стандартное но не модное описание гравитации.
Император Сарлака Грант Сциентикус III очень любил геометрию. И любовь его была настолько сильной, что однажды он решился на кощунство — проверить её экспериментально. Это было неслыханным делом: шутка ли, как можно геометрию, совершеннейшее детище чистой логики марать какими-то приземлёнными экспериментами? Сам великий геометр Хэфклит приехал посмотреть на это.
Ранним утром Грант отправил двух лучших планеристов в разные стороны, строго-настрого наказав им пролететь ровно сотню километров (на самом деле, расстояние было равно ста тридцати скелам, но это почти не отличается от ста километров) никуда не сворачивая, строго по прямой, сливая краску из прикрепленных к планерам баков по пути.
Как вы уже, наверное, поняли, таким способом он хотел проверить теорему о сумме углов треугольника. Пункт отправления двух планеристов и пункты их назначения должны были стать вершинами этого треугольника.
Не затягивая историю, сразу перейдём к кульминации: сумма углов оказалась больше, чем 180 градусов.
***
Здесь должно быть высокохудожественное и длинное описание всеобщего потрясения.
***
Хэфклит был настолько шокирован исходом эксперимента, что решил своими глазами посмотреть на горе-треугольник и прошёл ускоренные курсы полётов на планере. Давайте посмотрим на снимок того, что он увидел, любезно предоставленный нам спутником наблюдения, запущенным на орбиту Сарлака цивилизацией Птаагх, чьи представления о том, каким должен быть спутниковый снимок несколько отличаются от наших.
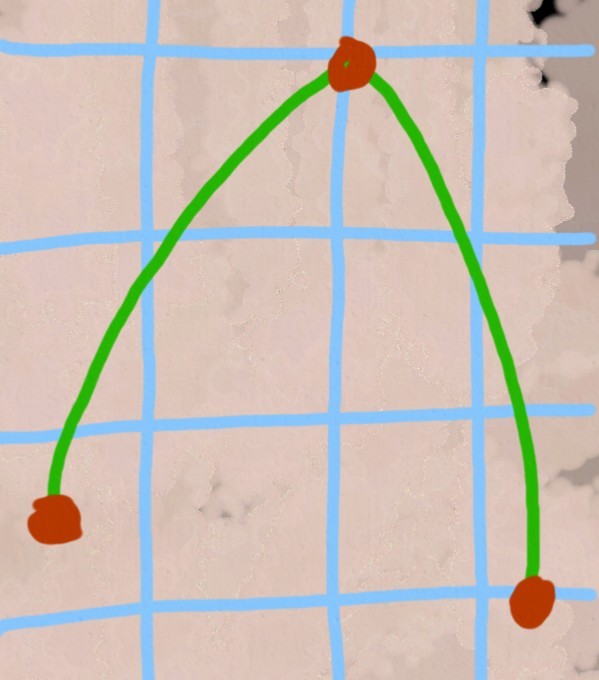
«Чёртовы летуны!» — воскликнул Хэфклит, «даже курс ровно выдержать не смогли!». Однако, на собрании, созванном во дворце Гранта по случаю открытия Хэфклита, «чёртовы летуны» заявили, что с курса не сбивались, и даже показали исписанные приборами ленты, по которым стало ясно, что они не поворачивали. И тут подал голос философ Ниу-Тан.
— Очевидно, — сказал он, — что и с летунами, и с геометрией всё в порядке. Я предполагаю, что линии полёта искривились из-за того, что на планеры действовала какая-то неизвестная нам сила, притягивающая их к центру треугольника.
Таким образом была спасена честь геометрии и найдена новая сила. А в уме Гранта родилось множество идей новых экспериментов.
Пожалуй, на этом мы могли бы закончить историю. Но, давайте посмотрим на ещё один из снимков спутника Птаагх:
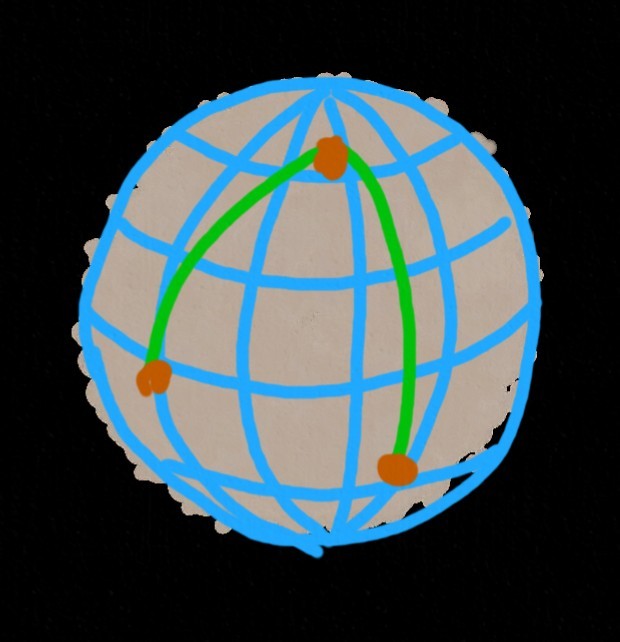
Видите? Вы видите это? Да, как вы уже догадались, никто из жителей Сарлака не знал, что они живут на поверхности шара (причём, довольно маленького). И кривизна линий объяснялась всего лишь тем, что сама поверхность, на которой они нарисованы, была кривой. Однако, если вы не знаете о кривизне, то лучшим возможным объяснением (за исключением оптических иллюзий и неопытности летунов) является наличие некой силы, искривляющий траектории планеров (и всего остального). Заметим, что эта сила будет действовать на все тела. Более того, на все эти тела она будет действовать одинаково.
Что-ж, у нас на виду есть одна такая сила. Она действует на всё, от неё невозможно укрыться, и её воздействие на все тела (а именно, ускорение придаваемое ею телам) одинаково. Как навязчиво подсказывает нам название публикации, это, конечно же, гравитация. К счастью, мы вовремя осознали, что гравитация — всего лишь проявление того, что пространство искривлено. Осознать это нам помог Альберт Эйнштейн, скромный служащий патентного бюро в Швейцарии и один из величайших учёных человечества (несомненно, когда-нибудь на Сарлаке молодой и талантливый философ Хэн-Штен тоже объяснит придуманную Ниу-Таном силу через кривизну).
Давайте наглядно увидим это искривление на примере камешков, пролетающих возле карликовой планеты (спасибо Птаагх):
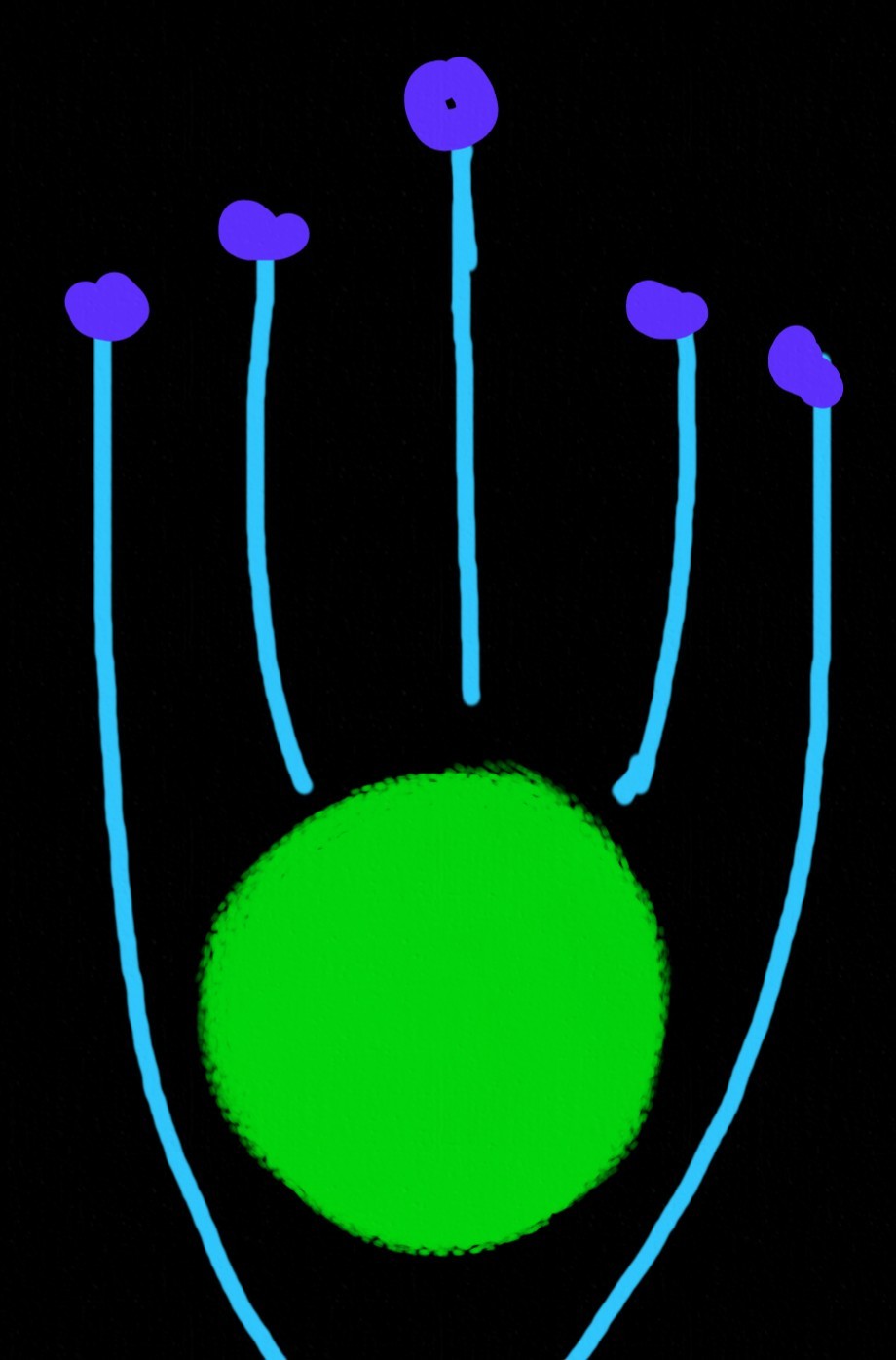
Птаагх услужливо отметили начальные положения камней и нарисовали их маршруты. Искривленные. Кроме среднего, который прямой. Что-то не так.
Мудрый Альберт понял так же и то, что пространство и время неотделимы друг от друга. Есть только единое пространство-время. И искривляется не только пространство, но и время. «Но!», скажешь ты, читатель, «как может время быть кривым?». Мы не будем углубляться в дебри и скажем лишь одно. Искривление времени наблюдается нами как ускорение. За равные промежутки времени наши камни будут проходить всё большее расстояние. Обратимся ещё раз к спутнику Птаагх:
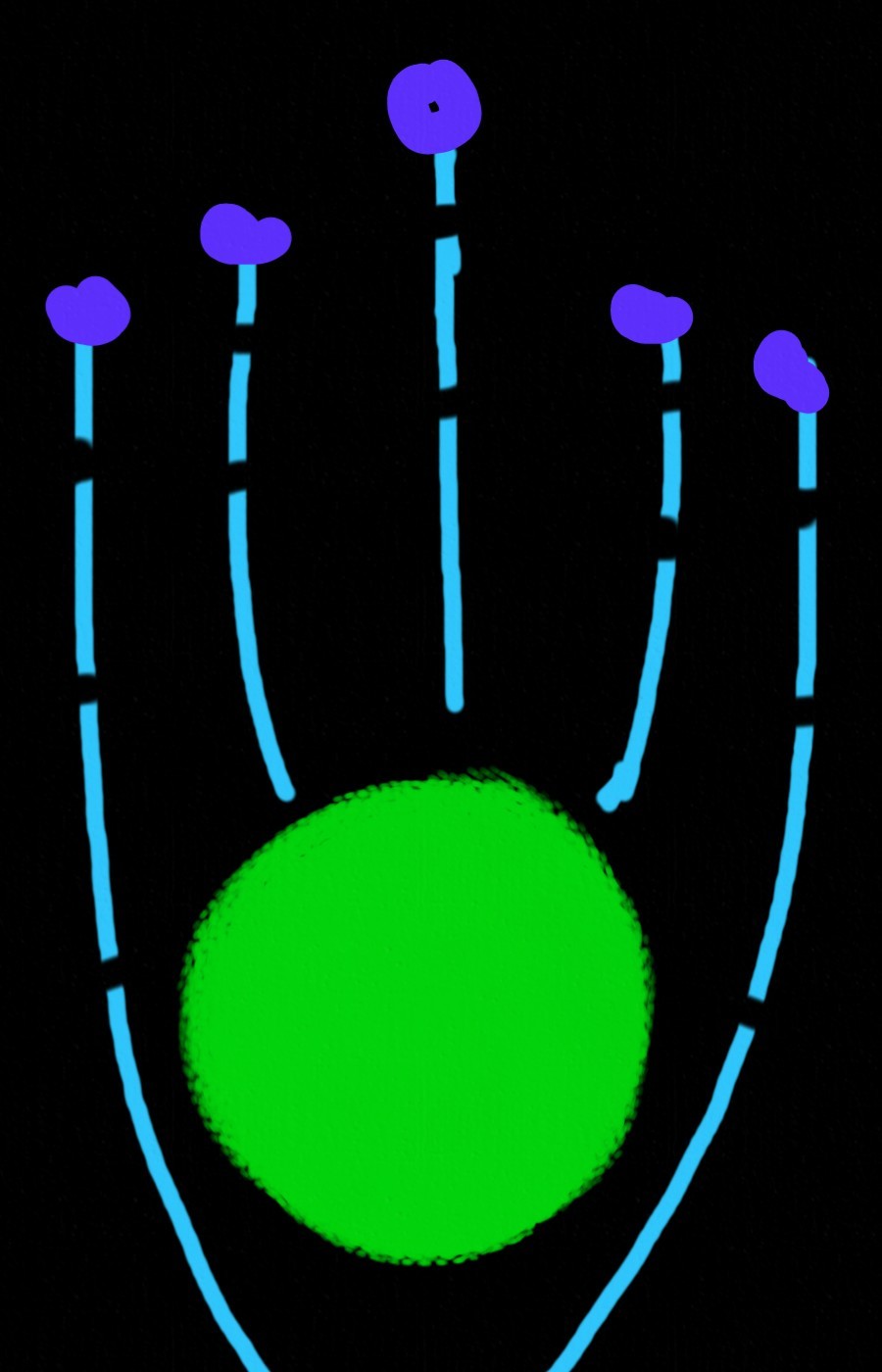
Здесь маршруты изображены не непрерывно, а в виде отдельных сегментов, пролёт каждого из которых занимает одно и то же время. Альберт прав!
Однако, нам известен ещё один случай, когда тела двигаются относительно нас с одним и тем же ускорением. Такое происходит, если мы сами двигаемся ускоренно. С нашей точки зрения всё окружающее будет перемещаться с одинаковым ускорением (тем самым, с которым перемещаемся мы, но направленным в противоположную сторону). Это сходство было отмечено Эйнштейном и названо им принцип эквивалентности. Как же отличить настоящее искривление пространства-времени от кажущегося, вызванного нашим ускоренным движением?
Птаагх расположили четыре камня в вершинах ромба недалеко от поверхности планеты, отпустили их и сделали два снимка в один кадр в разные моменты времени (стробоскопия):
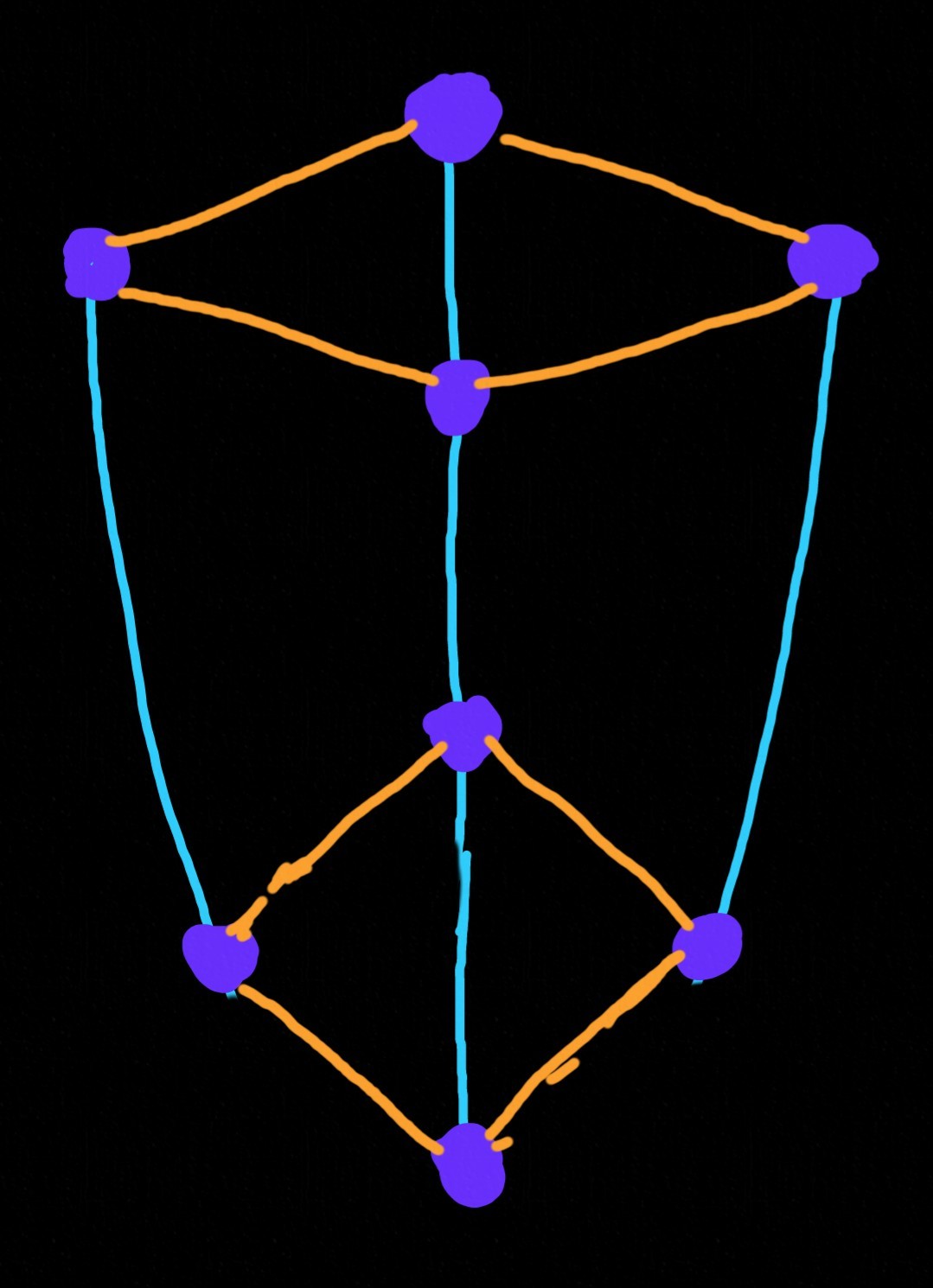
Ромб вытянулся в направлении «силы гравитации» и сжался в поперечном. Это происходит из-за того, что ускорения направлены не параллельно друг другу, а к центру планеты. И ускорение увеличивается, когда мы приближаемся к планете. В результате этого тела, которые ближе к планете, двигаются быстрее, а тела по бокам сходятся к середине.
Такое воздействие, растягивающее тело в направлении гравитации и сжимающее в поперечном, называется приливными силами. Именно приливные силы и являются настоящим проявлением гравитации.
Для математически подкованного читателя: метрика наблюдателя, покоящегося в поле гравитации локально совпадает с метрикой наблюдателя, перемещающегося с правильно подобранным ускорением. Совпадает и первая производная метрики. А вот вторая производная уже отличается, и именно она и является математическим «образом» приливных сил
Когда гравитация какого-нибудь тела или системы тел быстро меняется (как, например, при вращении двух чёрных дыр вокруг общего центра), «картина» искривления пространства-времени не успевает сгладиться, когда уже образуется новая. По пространству-времени идёт «рябь». Эту рябь мы называем гравитационными волнами. Воздействие гравитационных волн проявляется в виде периодического растяжения и сжатия пространства-времени в двух взаимно поперечных направлениях, то есть, в виде приливных сил. При этом, разделяют две разных поляризации гравитационных волн: (+) и (×).
Вот так проявляются (+)-поляризованные ГВ:
  
 
А вот так — (×)-поляризованные:
  
 
Синяя сетка здесь изображает пространство.
А теперь подумаем: можем ли мы как-то «почувствовать» эти волны? Ответ, — да, можем.
Представьте железный шар. Когда пространство, в котором он находится, начинает сжиматься и растягиваться, атомы, из которых он состоит, начинают сближаться в одном направлении и удаляться в другом. Однако, действующие между ними силы не дают им двигаться так свободно, как надо. В результате этого, деформация шара несколько отстаёт от деформации пространства-времени. Относительно пространства-времени шар начинает вибрировать, сжимаясь и растягиваясь. И вот такие вибрации могут дать нам знать, что прямо сейчас сквозь шар проходят ГВ. К сожалению, деформации очень малы: относительное изменение размеров под влиянием зарегистрированных в сентябре 2015 года ГВ равно десяти в минус двадцать первой степени. Я выпишу это число:
0.000000000000000000001
Если бы шар был в 3 раза меньше Земли, изменение его размера было бы равно диаметру одного протона. Поэтому, идея цельных детекторов ГВ несколько неудачна.
Сейчас вместо сплошных шаров используют полые «буквы Г», с бегущими внутри них лазерными лучами. Именно так устроен знаменитый LIGO. Изменения размеров «рукавов» детектора проявляются в виде изменений фаз лазерных лучей, которые можно определить в результате сложения двух лучей. Более подробно об этом я, возможно, напишу когда-нибудь потом. А тем, кому не терпится, рекомендую поиск по сайту по ключевой фразе «как регистрировали?». В статье товарища-гиктаймера, чьего никнейма я, к стыду своему, не помню, очень подробно и доходчиво описано, как работает LIGO.
Автор: tajimura
