Квантовая запутанность – одно из самых сложных понятий в науке, но основные её принципы просты. А если понять её, запутанность открывает путь к лучшему пониманию таких понятий, как множественность миров в квантовой теории.

Чарующей аурой загадочности окутано понятие квантовой запутанности, а также (каким-то образом) связанное с ним требование квантовой теории о необходимости наличия «многих миров». И, тем не менее, по сути своей это научные идеи с приземлённым смыслом и конкретными применениями. Я хотел бы объяснить понятия запутанности и множества миров настолько просто и ясно, насколько знаю их сам.
I
Запутанность считается явлением, уникальным для квантовой механики – но это не так. На самом деле, для начала будет более понятным (хотя это и необычный подход) рассмотреть простую, не квантовую (классическую) версию запутанности. Это позволит нам отделить тонкости, связанные с самой запутанностью, от других странностей квантовой теории.
Запутанность появляется в ситуациях, в которых у нас есть частичная информация о состоянии двух систем. К примеру, нашими системами могут стать два объекта – назовём их каоны. «К» будет обозначать «классические» объекты. Но если вам очень хочется представлять себе что-то конкретное и приятное – представьте, что это пирожные.
Наши каоны будут иметь две формы, квадратную или круглую, и эти формы будут обозначать их возможные состояния. Тогда четырьмя возможными совместными состояниями двух каонов будут: (квадрат, квадрат), (квадрат, круг), (круг, квадрат), (круг, круг). В таблице указана вероятность нахождения системы в одном из четырёх перечисленных состояний.
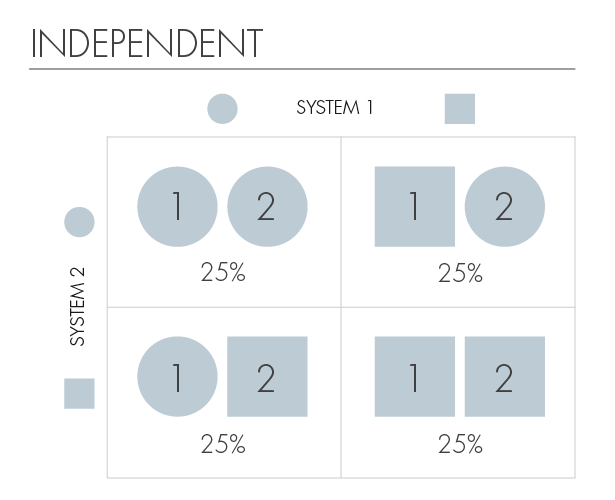
Мы будем говорить, что каоны «независимы», если знание о состоянии одного из них не даёт нам информации о состоянии другого. И у этой таблицы есть такое свойство. Если первый каон (пирожное) квадратный, мы всё ещё не знаем форму второго. И наоборот, форма второго ничего не говорит нам о форме первого.
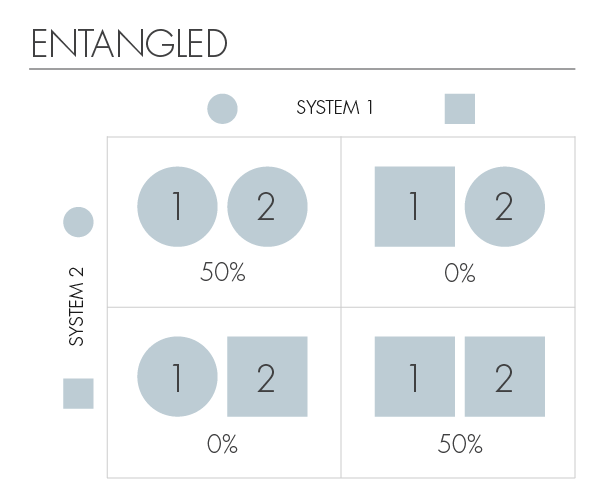
С другой стороны, мы скажем, что два каона запутаны, если информация об одном из них улучшает наши знания о другом. Вторая табличка покажет нам сильную запутанность. В этом случае, если первый каон будет круглым, мы будем знать, что второй тоже круглый. А если первый каон квадратный, то таким же будет и второй. Зная форму одного, мы однозначно определим форму другого.
Квантовая версия запутанности выглядит, по сути, также – это отсутствие независимости. В квантовой теории состояния описываются математическими объектами под названием волновая функция. Правила, объединяющие волновые функции с физическими возможностями, порождают очень интересные сложности, которые мы обсудим позже, но основное понятие о запутанном знании, которое мы продемонстрировали для классического случая, остаётся тем же.
Хотя пирожные нельзя считать квантовыми системами, запутанность квантовых систем возникает естественным путём – например, после столкновений частиц. На практике незапутанные (независимые) состояния можно считать редкими исключениями, поскольку при взаимодействии систем между ними возникают корреляции.
Рассмотрим, к примеру, молекулы. Они состоят из подсистем – конкретно, электронов и ядер. Минимальное энергетическое состояние молекулы, в котором она обычно и находится, представляет собой сильно запутанное состояние электронов и ядра, поскольку расположение этих составляющих частиц никак не будет независимым. При движении ядра электрон движется с ним.
Вернёмся к нашему примеру. Если мы запишем Φ■, Φ● как волновые функции, описывающие систему 1 в её квадратных или круглых состояниях и ψ■, ψ● для волновых функций, описывающих систему 2 в её квадратных или круглых состояниях, тогда в нашем рабочем примере все состояния можно описать, как:
Независимые: Φ■ ψ■ + Φ■ ψ● + Φ● ψ■ + Φ● ψ●
Запутанные: Φ■ ψ■ + Φ● ψ●
Независимую версию также можно записать, как:
(Φ■ + Φ●)(ψ■ + ψ●)
Отметим, как в последнем случае скобки чётко разделяют первую и вторую системы на независимые части.
Существует множество способов создания запутанных состояний. Один из них – измерить составную систему, дающую вам частичную информацию. Можно узнать, например, что две системы договорились быть одной формы, не зная при этом, какую именно форму они выбрали. Это понятие станет важным чуть позже.
Более характерные последствия квантовой запутанности, такие, как эффекты Эйнштейна-Подольского-Розена (EPR) и Гринберга-Хорна-Зейлингера (GHZ), возникают из-за её взаимодействия ещё с одним свойством квантовой теории под названием «принцип дополнительности». Для обсуждения EPR и GHZ позвольте мне сначала представить вам этот принцип.
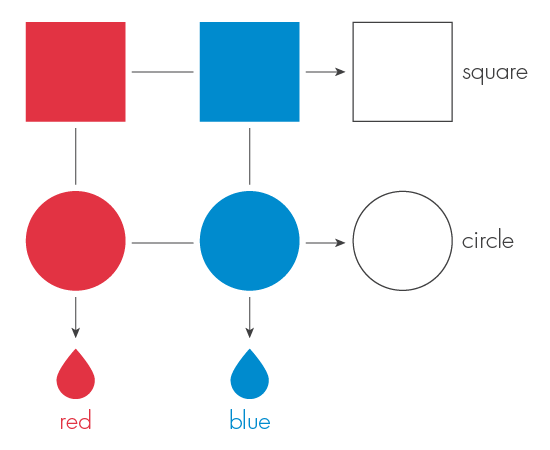
До этого момента мы представляли, что каоны бывают двух форм (квадратные и круглые). Теперь представим, что ещё они бывают двух цветов – красного и синего. Рассматривая классические системы, например, пирожные, это дополнительное свойство означало бы, что каон может существовать в одном из четырёх возможных состояний: красный квадрат, красный круг, синий квадрат и синий круг.
Но квантовые пирожные – квантожные… Или квантоны… Ведут себя совсем по-другому. То, что квантон в каких-то ситуациях может обладать разной формой и цветом не обязательно означает, что он одновременно обладает как формой, так и цветом. Фактически, здравый смысл, которого требовал Эйнштейн от физической реальности, не соответствует экспериментальным фактам, что мы скоро увидим.
Мы можем измерить форму квантона, но при этом мы потеряем всю информацию о его цвете. Или мы можем измерить цвет, но потеряем информацию о его форме. Согласно квантовой теории, мы не можем одновременно измерить и форму и цвет. Ничей взгляд на квантовую реальность не обладает полнотой; приходится принимать во внимание множество разных и взаимоисключающих картин, у каждой из которых есть своё неполное представление о происходящем. Это и есть суть принципа дополнительности, такая, как её сформулировал Нильс Бор.
В результате квантовая теория заставляет нас быть осмотрительными в приписывании свойствам физической реальности. Во избежание противоречий приходится признать, что:
Не существует свойства, если его не измерили.
Измерение – активный процесс, изменяющий измеряемую систему
II
Теперь опишем две образцовые, но не классические, иллюстрации странностей квантовой теории. Обе были проверены в строгих экспериментах (в реальных экспериментах люди меряют не формы и цвета пирожных, а угловые моменты электронов).
Альберт Эйнштейн, Борис Подольский и Натан Розен (EPR) описали удивительный эффект, возникающий при запутанности двух квантовых систем. EPR-эффект объединяет особую, экспериментально достижимую форму квантовой запутанности с принципом дополнительности.
EPR-пара состоит из двух квантонов, у каждого из которых можно измерить форму или цвет (но не то и другое сразу). Предположим, что у нас есть множество таких пар, все они одинаковые, и мы можем выбирать, какие измерения мы проводим над их компонентами. Если мы измерим форму одного из членов EPR-пары, мы с одинаковой вероятностью получим квадрат или круг. Если измерим цвет, то с одинаковой вероятностью получим красный или синий.
Интересные эффекты, казавшиеся EPR парадоксальными, возникают, когда мы проводим измерения обоих членов пары. Когда мы меряем цвет обоих членов, или их форму, мы обнаруживаем, что результаты всегда совпадают. То есть, если мы обнаружим, что один из них красный и затем меряем цвет второго, мы также обнаруживаем, что он красный – и т.п. С другой стороны, если мы измеряем форму одного и цвет другого, никакой корреляции не наблюдается. То есть, если первый был квадратом, то второй с одинаковой вероятностью может быть синим или красным.
Согласно квантовой теории, мы получим такие результаты, даже если две системы будет разделять огромное расстояние и измерения будут проведены почти одновременно. Выбор типа измерений в одном месте, судя по всему, влияет на состояние системы в другом месте. Это «пугающее дальнодействие», как называл его Эйнштейн, по-видимому, требует передачу информации – в нашем случае, информации о проведённом измерении – со скоростью, превышающей скорость света.
Но так ли это? Пока я не узнаю, какой результат получили вы, я не знаю, чего ожидать мне. Я получаю полезную информацию, когда я узнаю ваш результат, а не когда вы проводите измерение. И любое сообщение, содержащее полученный вами результат, необходимо передать каким-либо физическим способом, медленнее скорости света.
При дальнейшем изучении парадокс ещё больше разрушается. Давайте рассмотрим состояние второй системы, если измерение первой дало красный цвет. Если мы решим мерить цвет второго квантона, мы получим красный. Но по принципу дополнительности, если мы решим измерить его форму, когда он находится в «красном» состоянии, у нас будут равные шансы на получение квадрата или круга. Поэтому, результат EPR логически предопределён. Это просто пересказ принципа дополнительности.
Нет парадокса и в том, что удалённые события коррелируют. Ведь если мы положим одну из двух перчаток из пары в коробки и отправим их в разные концы планеты, неудивительно, что посмотрев в одну коробку, я могу определить, на какую руку предназначена другая перчатка. Точно так же, во всех случаях корреляция пар EPR должна быть зафиксирована на них, когда они находятся рядом и потому они могут выдержать последующее разделение, будто бы имея память. Странность EPR-парадокса не в самой по себе возможности корреляции, а в возможности её сохранения в виде дополнений.
III
Дэниел Гринбергер, Майкл Хорн и Антон Зейлингер открыли ещё один прекрасный пример квантовой запутанности. ОН включает три наших квантона, находящихся в специально подготовленном запутанном состоянии (GHZ-состоянии). Мы распределяем каждый из них разным удалённым экспериментаторам. Каждый из них выбирает, независимо и случайно, измерять ли цвет или форму и записывает результат. Эксперимент повторяют многократно, но всегда с тремя квантонами в GHZ-состоянии.
Каждый отдельно взятый экспериментатор получает случайные результаты. Измеряя форму квантона, он с равной вероятностью получает квадрат или круг; измеряя цвет квантона, он с равной вероятностью получает красный или синий. Пока всё обыденно.
Но когда экспериментаторы собираются вместе и сравнивают результаты, анализ показывает удивительный результат. Допустим, мы будем называть квадратную форму и красный цвет «добрыми», а круги и синий цвет – «злыми». Экспериментаторы обнаруживают, что если двое из них решили измерить форму, а третий – цвет, тогда либо 0, либо 2 результата измерений получаются «злыми» (т.е. круглыми или синими). Но если все трое решают измерить цвет, то либо 1 либо 3 измерения получаются злыми. Это предсказывает квантовая механика, и именно это и происходит.
Вопрос: количество зла чётное или нечётное? В разных измерениях реализовываются обе возможности. Нам приходится отказаться от этого вопроса. Не имеет смысла рассуждать о количестве зла в системе без связи с тем, как его измеряют. И это приводит к противоречиям.
Эффект GHZ, как описывает его физик Сидни Колман, это «оплеуха от квантовой механики». Он разрушает привычное, полученное из опыта ожидание того, что у физических систем есть предопределённые свойства, независимые от их измерения. Если бы это было так, то баланс доброго и злого не зависел бы от выбора типов измерений. После того, как вы примете существование GHZ-эффекта, вы его не забудете, а ваш кругозор будет расширен.
IV
Пока что мы рассуждаем о том, как запутанность не позволяет назначить уникальные независимые состояния нескольким квантонам. Такие же рассуждения применимы к изменениям одного квантона, происходящим со временем.
Мы говорим об «запутанных историях», когда системе невозможно присвоить определённое состояние в каждый момент времени. Так же, как в традиционной запутанности мы исключаем какие-то возможности, мы можем создать и запутанные истории, проводя измерения, собирающие частичную информацию о прошлых событиях. В простейших запутанных историях у нас есть один квантон, изучаемый нами в два разных момента времени. Мы можем представить ситуацию, когда мы определяем, что форма нашего квантона оба раза была квадратной, или круглой оба раза, но при этом остаются возможными обе ситуации. Это темпоральная квантовая аналогия простейшим вариантам запутанности, описанным ранее.
Используя более сложный протокол, мы можем добавить чуть-чуть дополнительности в эту систему, и описать ситуации, вызывающие «многомировое» свойство квантовой теории. Наш квантон можно подготовить в красном состоянии, а затем измерить и получить голубое. И как в предыдущих примерах, мы не можем на постоянной основе присвоить квантону свойство цвета в промежутке между двумя измерениями; нет у него и определённой формы. Такие истории реализовывают, ограниченным, но полностью контролируемым и точным способом, интуицию, свойственную картинке множественности миров в квантовой механике. Определённое состояние может разделиться на две противоречащие друг другу исторические траектории, которые затем снова соединяются.
Эрвин Шрёдингер, основатель квантовой теории, скептически относившийся к её правильности, подчёркивал, что эволюция квантовых систем естественным образом приводит к состояниям, измерение которых может дать чрезвычайно разные результаты. Его мысленный эксперимент с «котом Шрёдингера» постулирует, как известно, квантовую неопределённость, выведенную на уровень влияния на смертность кошачьих. До измерения коту невозможно присвоить свойство жизни (или смерти). Оба, или ни одно из них, существуют вместе в потустороннем мире возможностей.
Повседневный язык плохо приспособлен для объяснения квантовой дополнительности, в частности потому, что повседневный опыт её не включает. Практические кошки взаимодействуют с окружающими молекулами воздуха, и другими предметами, совершенно по-разному, в зависимости от того, живы они или мертвы, поэтому на практике измерение проходит автоматически, и кот продолжает жить (или не жить). Но истории с запутанностью описывают квантоны, являющиеся котятами Шрёдингера. Их полное описание требует, чтобы мы принимали к рассмотрению две взаимоисключающие траектории свойств.
Контролируемая экспериментальная реализация запутанных историй – вещь деликатная, поскольку требует сбора частичной информации о квантонах. Обычные квантовые измерения обычно собирают всю информацию сразу – к примеру, определяют точную форму или точный цвет – вместо того, чтобы несколько раз получить частичную информацию. Но это можно сделать, хотя и с чрезвычайными техническими трудностями. Этим способом мы можем присвоить определённый математический и экспериментальный смысл распространению концепции «множественности миров» в квантовой теории, и продемонстрировать её реальность.
Автор: SLY_G