Рэндзю 3-2 – игра полутора лиц без начала

Заголовок наверняка повергнет читателя в полное недоумение. Во‑первых, разве может число лиц быть нецелым? И как это — без начала? Сейчас расскажем!

Итак, все по порядку.

Во-первых, дробь выражает всего лишь несовпадение лиц — независимых сторон в игровом противостоянии — с реальными участниками игры. Такое наблюдается в некоторых играх с неполной информацией (например, картежных), когда участники разбиваются на коалиции (команды). При этом каждое лицо можно считать представленным несколькими участниками.

Превратить одно лицо в коалицию не составляет труда и в классических играх двух лиц с полной информацией — шахматах, шашках и др. На занятиях по логическим играм автор, для развития у детей «коллективного сознания», предлагает играть двум командам за два лица соответственно. Ходы за каждую сторону члены команды совершают по очереди. Соотношение числа игроков в командах может быть произвольным: один против двух, двое против трех и т. д. Если один из членов команды делает ошибочный ход, ведущий к быстрому проигрышу, страдает вся команда.

В рэндзю 3/2 несовпадение лиц с участниками реализуется радикальным, на первый взгляд, парадоксальным образом. Здесь два участника как бы растворяются в трех лицах — то есть число лиц оказывается не только бóльшим, чем число участников, но к тому же и взаимно простым с ним! Чисто практически это достигается равномерным распределением игрового материала, принадлежащего трем условным лицам, между двумя реальными игроками. Иными словами, каждый из двух игроков пользуется, причем в равноценной степени, игровым материалом всех трех условных лиц.

Последнее обстоятельство обессмысливает дебют. Дело в том, что выигрыш в рэндзю 3/2 достигается построением определенной конфигурации (о ней поговорим позже), к которой приводит комбинационная атака. Но получается, что предпосылки для проведения атаки создаются противником: ведь игровой материал равномерно распределен между игроками. В результате складывается ситуация, когда ни одному из игроков невыгодно вообще начинать партию. Тем не менее, игра имеет смысл, но… только если начальная конфигурация уже задана. Перейдем к описанию игры.

Игровое поле, как и в рэндзю для троих, — квадрат, поделенный на 19х19 = 361 клеток (рис. 1).

Рисунок 1

Оба игрока — обозначим их как A и B — имеют в распоряжении три набора фишек (или камней, как принято выражаться применительно к восточным играм) определенного цвета — голубого, красного и зеленого. Будем обозначать их буквами «г», «к» и «з» соответственно.

Вместо фишек можно использовать графические знаки, например, крестик «x», нолик «о», плюсик «+», и выписывать их на бумагу в клетку.

Ход состоит в выставлении двух фишек разного цвета соответственно на две свободные клетки поля, где они остаются до конца партии. Выставление каждой фишки по отдельности назовем полуходом.

Ходы совершаются игроками поочередно по следующей схеме: A[г, к] → B[з, г] → A[к, з] → B[г, к] → A[з, г] → B[к, з] → A[г, к]…, причем допускается пропуск как полухода, так и целого хода.

Вышеприведенная схема читается так: первым ходом игрок A может выставить синюю и красную фишки; следующим ходом игрок B может выставить зеленую и синюю фишки и т. д. Поэтому будем называть данную схему потенциальной последовательностью ходов, а последовательность, составленную из реальных ходов, — актуальной.

Допустим, игроку A, согласно потенциальной последовательности, полагается совершить ход [к, з]. Он при этом может выставить обе фишки (красную и зеленую) или одну из них (красную или зеленую), либо вообще не выставлять фишек. Независимо от его реальных действий, игрок B отвечает ходом [г, к], который, в свою очередь, может быть совершен аналогичными тремя способами.

Потенциальная последовательность ходов, как нетрудно заметить, циклична, ее период равен шести (мы выделили жирным шрифтом ее повторяющиеся первый и седьмой члены). Цвета фишек в ней тоже меняются циклически с периодом 3: г → к → з → г… В актуальной последовательности ходов цикличность может нарушаться.

Для практических целей потенциальную последовательность ходов удобно записывать в виде таблицы, состоящей из двух столбцов: в первом записываются ходы игрока A, во втором — игрока B. Циклы из шести ходов при этом отграничиваются друг от друга горизонтальной чертой (рис. 2).

В процессе партии сделанные полуходы можно вычеркивать. На рис. 3 приведены примеры первых шести ходов.

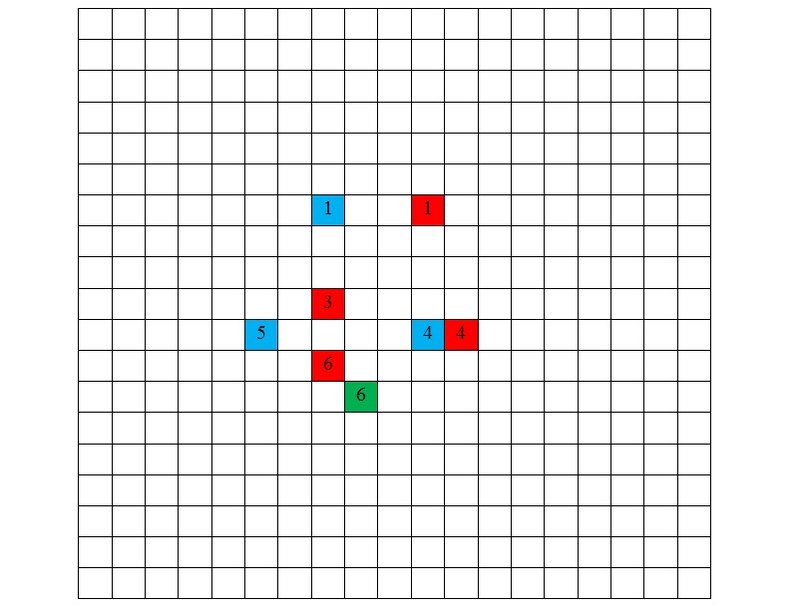Рисунок 3

Выигрывает тот, кто первым сумеет построить четверку из рядом стоящих фишек одного цвета по вертикали, горизонтали или по одной из диагоналей (рис. 4).

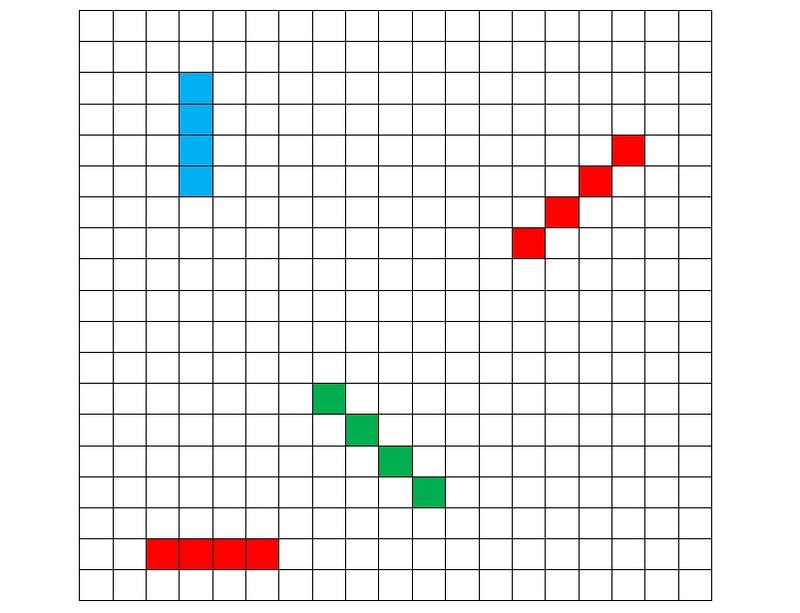Рисунок 4

Ряд из большего числа знаков не считается ни выигрышным, ни проигрышным.

Если пропущено 6 ходов подряд, то есть полный цикл потенциальной последовательности, объявляется ничья.

На первый взгляд, кажется, что за исключением тривиального случая — выставления четверки, ни при какой начальной конфигурации невозможно построить связной атаки. Оказывается, это совершенно не так. На рис. 5a приведен пример начальной конфигурации, порождающей многоходовую атаку. Для экономии места мы используем лишь часть игрового поля.

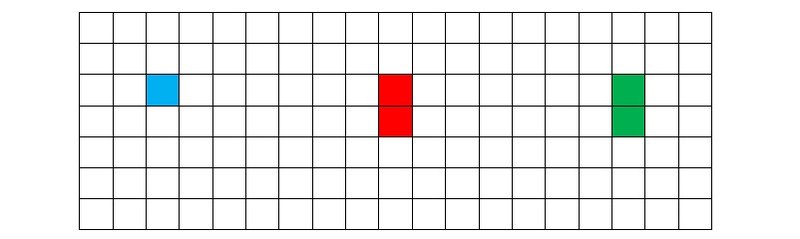Рисунок 5а

Игрок A, начинающий потенциальную последовательность, первым полуходом выстраивает голубую открытую двойку, а вторым — красную открытую тройку (рис. 5b).

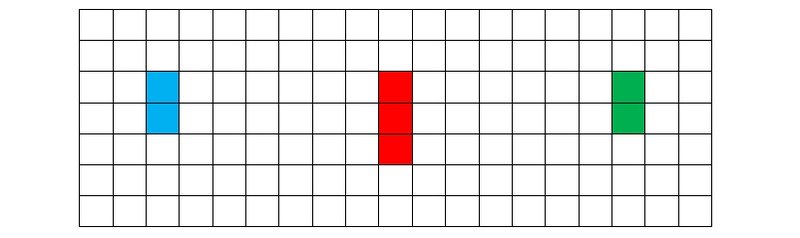Рисунок 5b

Поскольку игрок A грозит выставить через ход красную четверку, B ответным ходом вынужден закрыть красную тройку зеленой и голубой фишкой (рис. 5c).

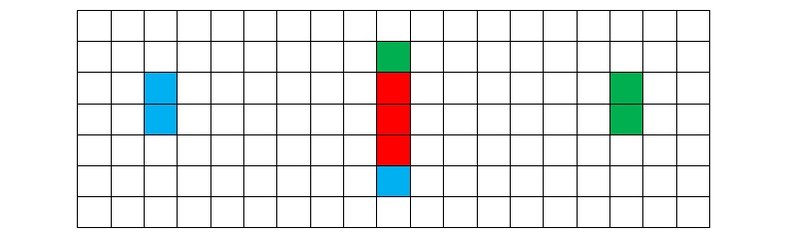Рисунок 5c

Дальнейшая стратегия игрока A очевидна. Каждым первым полуходом он выставляет открытую двойку, а вторым — открытую тройку, угрожая превратить ее через ход в четверку (рис. 5d-s).

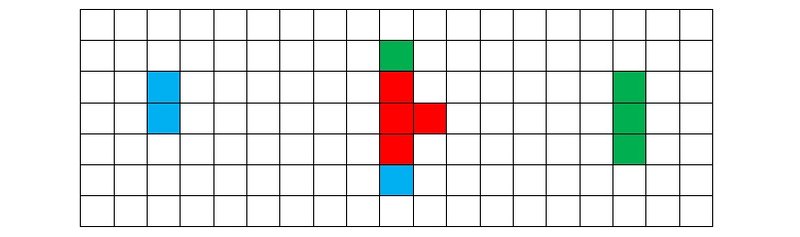Рисунок 5d

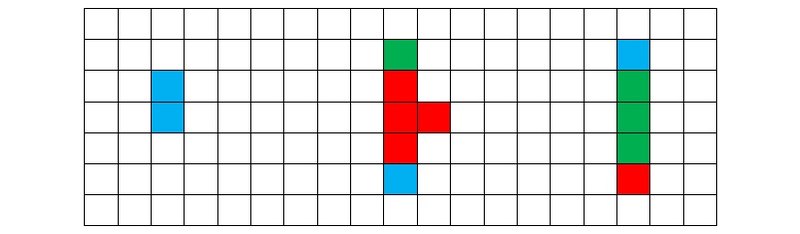Рисунок 5e

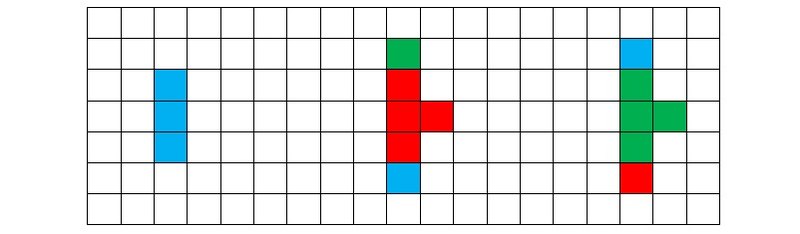Рисунок 5f

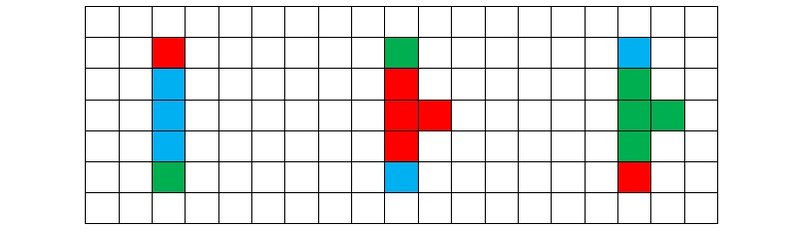Рисунок 5g

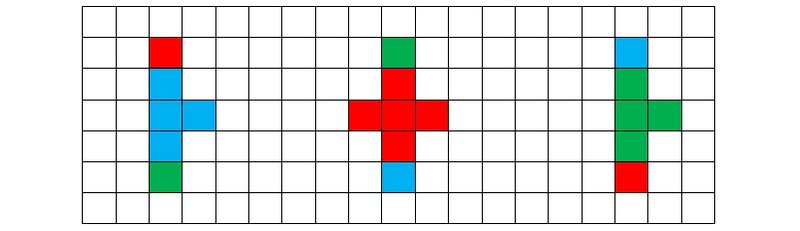Рисунок 5h

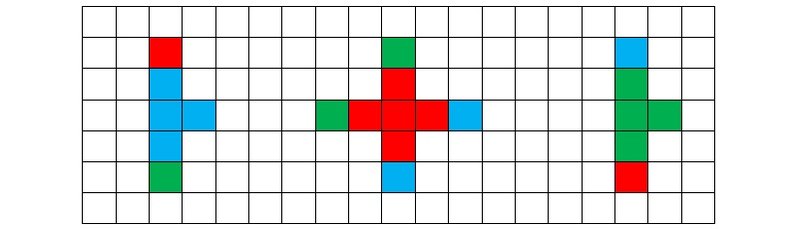Рисунок 5i

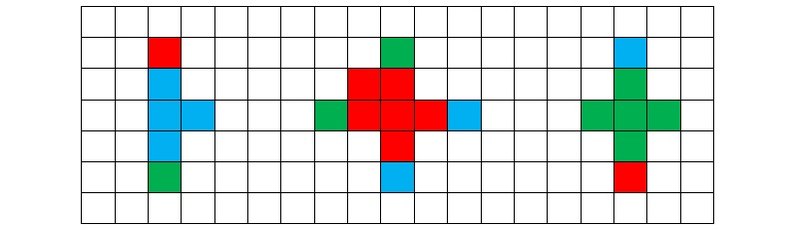Рисунок 5j

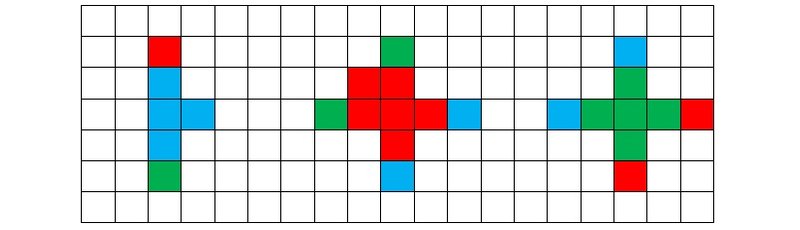Рисунок 5k

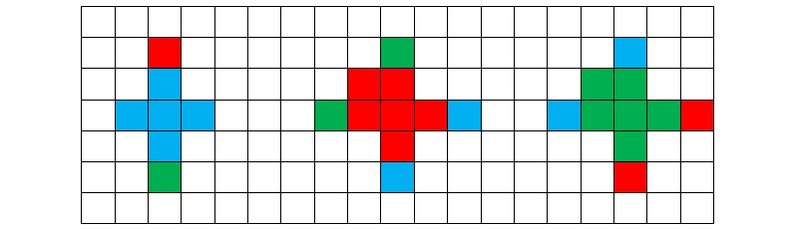Рисунок 5l

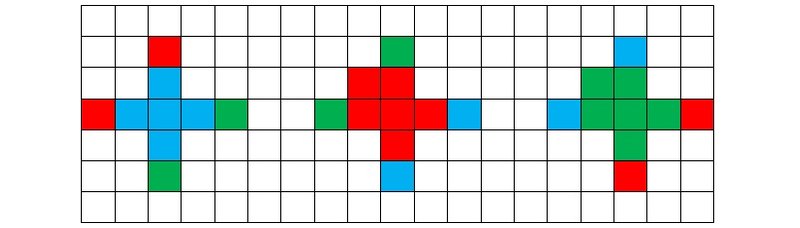Рисунок 5m

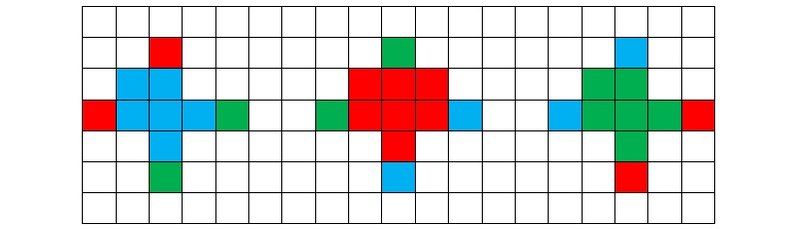Рисунок 5n

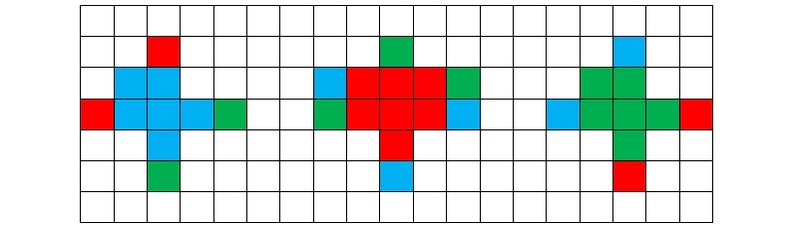Рисунок 5o

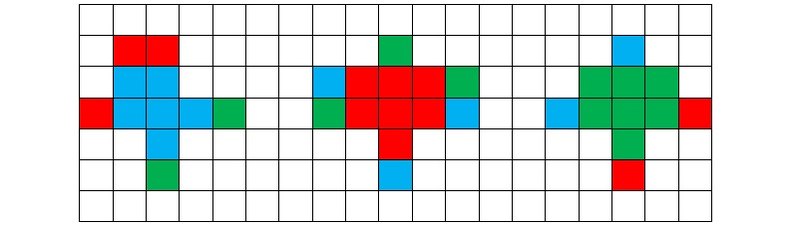Рисунок 5p

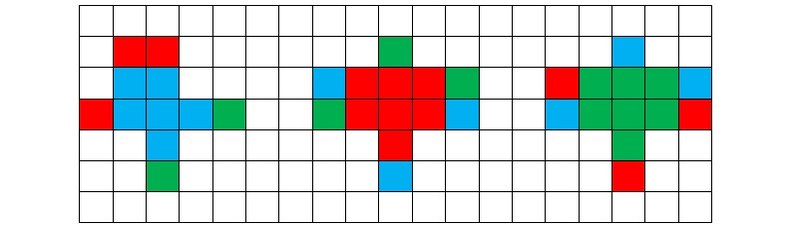Рисунок 5q

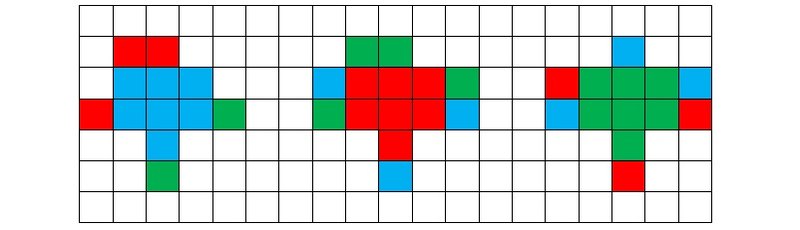Рисунок 5r

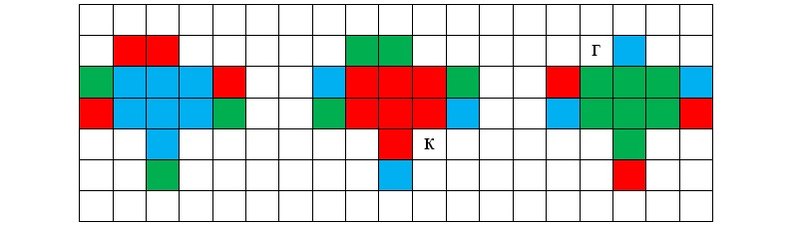Рисунок 5s

В данной ситуации игроку A остается вторым полуходом выставить красную фишку в клетку, помеченную буквой «к» и сделать вилку из двух открытых троек. Первый полуход голубой фишкой он может пропустить или — из чисто эстетических соображений — выставить ее в клетку, помеченную буквой «г».

В результате получим финальную позицию, приведенную на рис. 5t.

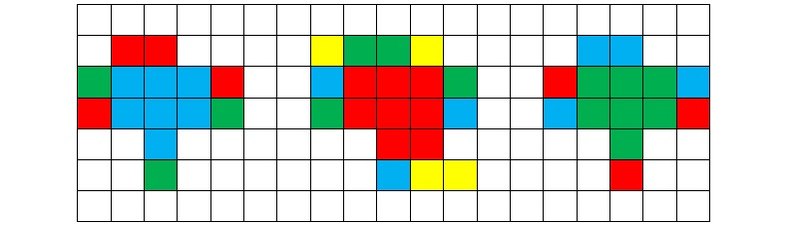Рисунок 5t

Игрок B не в состоянии закрыть сразу четыре критических клетки (они выделены желтым цветом). Итак, игрок A выиграл на 21-м ходу (включая выставление четверки).

Рассмотрим отдельно позицию перед последним полуходом игрока A — в момент, когда он выставил голубую фишку, но еще не выставил красную (рис. 6).

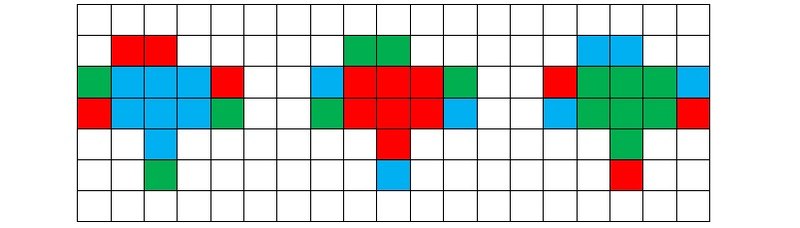Рисунок 6

Читатель без труда заметит красивую закономерность в чередовании цветов эквивалентных частей этих трех конгруэнтных фигур. Данную позицию можно неограниченно продолжить в обе стороны (рис. 7).

Рисунок 7

Полученная бесконечная фигура (на рисунке мы приводим ее фрагмент) обладает трансляционной цветной симметрией: с одной стороны, она имеет в качестве элемента симметрии горизонтальную ось параллельного переноса; с другой стороны, при каждом таком переносе цветá эквивалентных частей повторяющейся фигуры меняются циклически. Цветная симметрия — частный случай антисимметрии, когда цветов только два (например, черный и белый). Перенос с изменением цвета в этом случае называется антипереносом (по терминологии А. В. Шубникова). Для обобщенной цветной симметрии порядка n такого рода перенос можно назвать цветным переносом n-го порядка. Для нашей фигуры порядок цветного переноса равен трем.

Приведенный выше пример многоходовой атаки показывает, что такие атаки в принципе возможны. На самом деле он описывает и стандартный атакующий механизм: первым полуходом выстраивается открытая двойка, вторым — открытая тройка. Все остальные тактические приемы представляют собой, в основном, разного рода ловушки, рассчитанные на невнимательность противника. Так как игровым материалом в равной степени пользуются оба игрока, ни о каком наращивании преимущества речи идти не может.

В заключение приведем две возможные начальные конфигурации (рис. 8a-b).

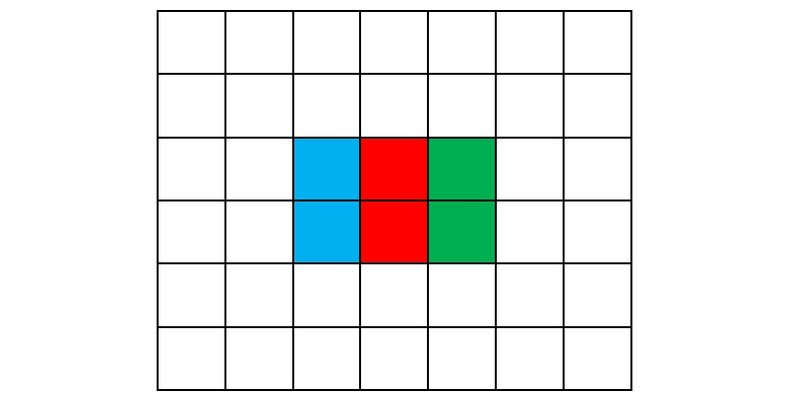Рисунок 8a

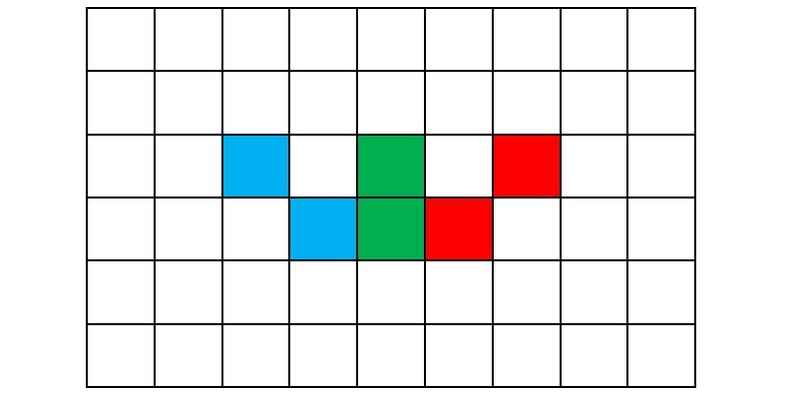Рисунок 8b

Разыграйте их с партнером. Придумайте новые начальные конфигурации.

Можно ли для них однозначно определить, для какой стороны они являются выигрышными?

Источник

Источник